Let 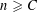 $n\geqslant C$ for a large universal constant
$n\geqslant C$ for a large universal constant 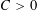 $C>0$ and let
$C>0$ and let 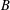 $B$ be a convex body in
$B$ be a convex body in 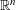 $\mathbb{R}^{n}$ such that for any
$\mathbb{R}^{n}$ such that for any 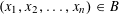 $(x_{1},x_{2},\ldots ,x_{n})\in B$, any choice of signs
$(x_{1},x_{2},\ldots ,x_{n})\in B$, any choice of signs 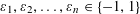 $\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{n}\in \{-1,1\}$ and for any permutation
$\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{n}\in \{-1,1\}$ and for any permutation  $\unicode[STIX]{x1D70E}$ on
$\unicode[STIX]{x1D70E}$ on  $n$ elements, we have
$n$ elements, we have 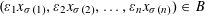 $(\unicode[STIX]{x1D700}_{1}x_{\unicode[STIX]{x1D70E}(1)},\unicode[STIX]{x1D700}_{2}x_{\unicode[STIX]{x1D70E}(2)},\ldots ,\unicode[STIX]{x1D700}_{n}x_{\unicode[STIX]{x1D70E}(n)})\in B$. We show that if
$(\unicode[STIX]{x1D700}_{1}x_{\unicode[STIX]{x1D70E}(1)},\unicode[STIX]{x1D700}_{2}x_{\unicode[STIX]{x1D70E}(2)},\ldots ,\unicode[STIX]{x1D700}_{n}x_{\unicode[STIX]{x1D70E}(n)})\in B$. We show that if 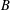 $B$ is not a cube, then
$B$ is not a cube, then 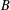 $B$ can be illuminated by strictly less than
$B$ can be illuminated by strictly less than 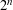 $2^{n}$ sources of light. This confirms the Hadwiger–Gohberg–Markus illumination conjecture for unit balls of
$2^{n}$ sources of light. This confirms the Hadwiger–Gohberg–Markus illumination conjecture for unit balls of 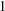 $1$-symmetric norms in
$1$-symmetric norms in 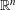 $\mathbb{R}^{n}$ for all sufficiently large
$\mathbb{R}^{n}$ for all sufficiently large  $n$.
$n$.
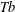 $\mathit{Tb}$ THEOREMS FOR SQUARE FUNCTIONS
$\mathit{Tb}$ THEOREMS FOR SQUARE FUNCTIONS
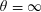 $\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
$\unicode[STIX]{x1D703}=\infty$ CONJECTURE IMPLIES THE RIEMANN HYPOTHESIS
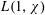 $L(1,\unicode[STIX]{x1D712})$ FOR
$L(1,\unicode[STIX]{x1D712})$ FOR 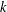 $k$TH ORDER CHARACTERS
$k$TH ORDER CHARACTERS 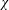 $\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
$\unicode[STIX]{x1D712}$ AND APPLICATIONS TO CHARACTER SUMS
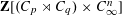 $\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE
$\mathbf{Z}[(C_{p}\rtimes C_{q})\times C_{\infty }^{n}]$ ARE FREE