A unified theory of slender wings in asymmetric motion, with an application to a swimming sea snake

Abstract

The slender body theory is extended to accommodate cases where a wing, in generally non-uniform motion, sideslips at sufficiently large angle to make the flow separate from one of its long edges but not from any part of the other. In those cases, an approximately triangular wake forms to the side of the wing, rendering the pressure loads on the wing not only asymmetrical, but also dependent on the history of the wing's motion. The theory can have a wide range of possible applications, from estimating lift and drag of a slender wing in pronouncedly asymmetric flight, through analysing an aero-elastic stability of that wing, to estimating thrust, lift and power of a sea snake that swims at an angle to its body axis. Coherence of the theory is demonstrated through numerous numerical simulations.

1. Introduction

Oblique (or asymmetrically swept) wings can be envisioned as sailplane-like high-aspect-ratio straight wings that fly at notable sideslip angles. They were extensively studied at small to moderate sweep angles (e.g. Cheng 1978; Guermond & Sellier 1991), with the idea of becoming a viable alternative to conventional wings at transonic and supersonic speeds (Jones 1977). Slender symmetrical wings were extensively studied as well, with uncountable applications in aerospace vehicles (e.g. Ashley & Landahl 1985) and aquatic locomotion (e.g. Lightill 1960). However, highly swept oblique wings, which can formally be categorized as asymmetric slender configurations, have been practically unnoticed. Naturally representing slender wings in asymmetric flight, these configurations can also be found in non-rotating blades of a helicopter on a windy platform, stern oars during sculling or steering, flapping narrow flags and some swimming sea snakes. What sets these configurations apart from widely studied oblique wings is their slenderness; what sets them apart from widely studied slender wings and bodies is their pronounced asymmetry with respect to the oncoming flow: one of the long edges of the wing ‘leads’ for its entire length, and at least a part of the other edge ‘trails’, with an inherently asymmetric wake forming to its side (figure 1). In fact, the yellow-bellied sea snakes Hydrophis platurus enter the list of asymmetric slender configurations because they swim at an angle to their body axis, the rounded back leading the cusped belly (Graham et al. 1987). Aero- (hydro-) dynamic theory of slender asymmetric configurations in generally non-uniform motion at high Reynolds numbers and subsonic speeds is the subject matter of this study.

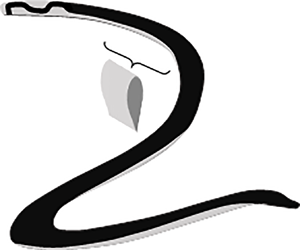
Figure 1. Side (a) and top (b) views of the model body and its wake (shaded). The body is naturally divided into two segments, forward $({x_n},0)$ and aft $(0,{x_t})$. The flow separates from the upper (‘+’) edge of the aft segment and forms a well-defined wake. It does not separate from the lower (‘−’) edge for its entire length, and it does not separate from the upper edge of the forward segment.

Limiting the scope of the study to high Reynolds numbers opens the possibility of using potential theories to find the velocity and pressure fields in the exterior of the boundary layer around the body and the wake behind it without finding them in their rotational interior; limiting the scope to slender configurations opens the possibility of obtaining these fields asymptotically, based on the ratio of the lateral and longitudinal length scales of the wing as a small parameter. Indeed, quite a few asymptotic potential theories of slender bodies at high Reynolds have been developed over the years, differing in the rigor of their construction, geometrical features of the body, modes of motion and geometry of the wake. Foundations of this study are found in the works of Wu (1971), Neumann & Wu (1973), Yates (1983) and Lighthill & Blake (1990); the starting point of this study is the theory of slender bodies in asymmetric motion with no wake to the side of them (Iosilevskii & Rashkovsky 2020). The last work is referred to as ‘Part 1’ below.

The paper is organized in 8 sections and 8 appendices. The problem is formally introduced in the next section (§ 2); its general solution is outlined in § 3. Particular solutions for the forward and aft segments of the body – the aft segment starts where the wake does, as in figure 1 – are presented in §§ 4 and 5, respectively. They are combined in § 6 to obtain forces and moments acting on the entire body, as well as the power needed to sustain its motion. A few examples from the problems mentioned earlier are shown in § 7, and this is where the coherence of the theory is tested by comparison with numerical simulations based on the vortex lattice method. A comparison with a few numerical simulations based on Reynolds-averaged Navier–Stokes (RANS) equations is found in the supplementary material available at https://doi.org/10.1017/jfm.2022.192. Section 8 concludes the paper. Appendices A–E detail derivations of a few key equations; Appendices F and G detail a few useful approximations of the indicial functions and their quadratures; Appendix H details the numerical simulations.

2. Preliminaries

2.1. The model

Consider a slender body that moves, on average, along a straight path with constant speed v in an unbounded domain of incompressible fluid of density ρ. The body is assumed flat and of zero thickness, but is allowed to deform with time in such a way that its (otherwise straight) cross-sections preserve both shape and dimensions (figure 2). Still, it can bend and twist, and small-amplitude lateral and torsional displacement waves can propagate along it, mimicking propulsion waves of an anguilliform (eel-like) swimmer.

Figure 2. Exaggerated lateral (a) and torsional (b) displacement waves. Model wake is light shaded. Global (primed) and local (unprimed) reference frames are shown in black and red. The particular local reference frame that is shown on both plates is adjacent to the red-coloured (last) cross-section.

The upper edge of the body will be universally marked by a ‘+’, the lower edge will be marked by a ‘−’. Association of these edges with ventral and dorsal sides of a swimming animal or with the edges of a flying wing will be made ad hoc as needed. The body is assumed to comprise two distinct segments, divided in figure 1 by the y-axis. The width (span) 2s of the forward segment is assumed to increase monotonically along it, reaching $2{s_0}$ at its aft end; both edges of this segment, upper and lower alike, face the flow (and hence function as leading edges) at all times. The width 2s of the aft segment will be ultimately assumed constant $2{s_0}$, with both edges forming a constant (strictly positive, but small) angle $\lambda $ with the direction of flow; at this stage, however, it suffices to assume that the lower and upper edges of this segment are ‘leading’ and ‘trailing’ at all times, respectively. ${s_0}$, v, ${s_0}/v$, ${s_0}v$, $\rho {v^2}$, $\rho {v^2}{s_0}$, $\rho {v^2}s_0^2$, $\rho {v^2}s_0^3$, $\rho {v^3}{s_0}$ and $\rho {v^3}s_0^2$ will be implicitly used below as units of length, velocity, time, potential, pressure, force per unit length, force (or moment per unit length), moment, power per unit length and power, respectively.

2.2. Reference frames

Two adjunct right-handed rectilinear reference frames, C and C′, will be used interchangeably. Both have their x-axes opposing the (average) direction of motion, and both follow the body along its average path. Frame C′ is a global (inertial) frame, its y-axis lays in the mid plane of the un-deformed body, and, for the sake of definiteness, points upwards through the upper tip of the body – where the leading edge of the forward segment turns into the trailing edge of the aft one (figures 1 and 2). The complementary z-axis points left. Coordinates of a point relative to C′ will be marked by a prime. Any scalar or vector field parametrized using these coordinates will be marked by a prime as well.

Frame C is a local (non-inertial) reference frame, affixed to each cross-section of the body. Its origin is located in the $y^{\prime}- z^{\prime}$ plane of C′, its x-axis passes through the middle of a particular section and the frame itself is rotated (twisted) about the x-axis through (a supposedly small) angle $\theta (t,x)$, so as to make the y-axis parallel to that section (figure 2). Coordinates of a point relative C will remain unmarked, and so will any scalar or vector field parametrized using these coordinates. Formally,

(2.1)\begin{gather}{\boldsymbol{e}_{x^{\prime}}} = {\boldsymbol{e}_x},\end{gather}

(2.2)\begin{gather}{\boldsymbol{e}_{y^{\prime}}} = {\boldsymbol{e}_y} - {\boldsymbol{e}_z}\theta (t,x),\end{gather}

(2.3)\begin{gather}{\boldsymbol{e}_{z^{\prime}}} = {\boldsymbol{e}_y}\theta (t,x) + {\boldsymbol{e}_z}\end{gather}

relate the respective unit vectors;

(2.4)\begin{gather}x^{\prime} = x,\end{gather}

(2.5)\begin{gather}y^{\prime} = {y_0}(x) - z\theta (t,x) + y,\end{gather}

(2.6)\begin{gather}z^{\prime} = {z_0}(t,x) + z + y\theta (t,x)\end{gather}

relate the coordinates. Because of their equivalence, $x^{\prime}$ and x (as well as ${\boldsymbol{e}_{x^{\prime}}}$ and ${\boldsymbol{e}_x}$) will be used interchangeably; ${x_n}$ and ${x_t}$ (primed or unprimed, but mostly unprimed) will mark the respective coordinates of the forward and aft ends of the body (figure 1).

2.3. Unit normal vectors

By interpretation, $y^{\prime} = {y_0}(x)$ and $z^{\prime} = {z_0}(t,x)$ are equations of the body centreline in C′; $y^{\prime} = {y_0}(x) \pm s(x)$ and $z^{\prime} = {z_0}(t,x) \pm s(x)\theta (t,x)$ are equations of its respective (‘+’ and ‘−’) edges in the same reference frame, and, in general,

(2.7)\begin{equation}z^{\prime} = {z_0}(t,x) + y\theta (t,x)\end{equation}

is the equation of its surface; $\theta $ is the twist angle of the particular section relative to the $x^{\prime}{-} y^{\prime}$ plane. All spatial derivatives of ${y_0}$, ${z_0}$, and θ are assumed small compared with unity. Accordingly,

(2.8)\begin{equation}\boldsymbol{n}(t,x) ={-} {\boldsymbol{e}_{x^{\prime}}}\left( {\frac{{\partial {z_0}(t,x)}}{{\partial x}} - \theta (t,x)\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.7pt x}} + y\frac{{\partial \theta (t,x)}}{{\partial x}}} \right) - {\boldsymbol{e}_{y^{\prime}}}\theta (t,x) + {\boldsymbol{e}_{z^{\prime}}} + \ldots\end{equation}

is the (left-facing) unit normal vector to the surface of the body;

(2.9)\begin{equation}{\boldsymbol{n}_ \pm }(t,x) ={-} {\boldsymbol{e}_{x^{\prime}}}\left( { \pm \theta (t,x)\frac{{\partial {z_0}(t,x)}}{{\partial x}} \pm \frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}} + \frac{{\textrm{d}s(x)}}{{\textrm{d}\kern0.06em x}}} \right) \pm {\boldsymbol{e}_{y^{\prime}}} \pm {\boldsymbol{e}_{z^{\prime}}}\theta (t,x) + \ldots \end{equation}

are the unit normal vectors to its respective edges. The ellipses stand for the higher-order terms with respect to spatial derivatives of ${z_0}$, ${y_0}$ and θ. Essentially, these are variants of (A6)–(A8) and (A11) of Part 1 with $|\theta |\ll 1$.

3. Slender body theory

3.1. Basics

As mentioned already, an attempt is made here to extend the slender (elongated) body theory to the case where the wake exists to one side of the body only. Formulation of the slender body theory can be found in quite a few references – notably, Ashley & Landahl (1985), Wu (1971) and Newman & Wu (1973) – and it will not be repeated. Its (implicit) basics are recapitulated below, preserving the notation of Part 1.

The slender body theory is usually constructed in the framework of the potential flow approximation, which, in turn, is coherent under two fundamental assumptions. One is that vortical regions in the flow are confined to a thin boundary layer around the body and a thin wake behind it, whereas the flow is irrotational in their exterior (Thwaites 1960). The other is that the boundary layer separates at the sharp trailing edges of the body and this is where it turns into the wake (Thwaites 1960; Katz & Plotkin 1991). Under these two assumptions, the velocity and pressure fields can be found in the exterior of the vortical regions, without finding them in the entire domain occupied by the fluid. The slender body theory furnishes these fields in the leading order with respect to a slenderness parameter, which is a certain ratio of the lateral (along the y'- or z'- axes) and longitudinal (along the x-axis) characteristic length scales.

When the thickness of the vortical regions is (vanishingly) small, a change in momentum of the fluid in their exterior is effected through the pressure on the outer edge of the boundary layer, which is essentially the same as the pressure (normal stress) on the surface of the body. A change in momentum of the fluid in the interior of the vortical regions is effected mainly through shear stresses on the surface of the body. In the case of a self-propelling body, this natural subdivision allows for unambiguous separation of thrust and (viscous) drag, associating thrust with the normal stresses and drag with the shear ones; the work done by the body is associated with the normal stresses only. Induced drag is akin to thrust in steady motion, and hence is associated with the normal stresses as well. In other words, the slender body theory allows for the finding of all relevant aerodynamic forces acting on the body, except for the viscous drag. The viscous drag is not addressed in this paper, but in many practical cases it can be closely estimated using empirical methods (Raymer 1992).

3.2. Boundary integral equation

In the leading order with respect to the slenderness parameter, the slender body theory reduces the problem of finding the velocity and pressure fields in the irrotational proximity of the body to that of finding a certain scalar field ϕ that satisfies two-dimensional Laplace equation in every transverse (y–z) plane crossing the body, satisfies an impermeability condition on its surface, has no pressure discontinuity across the wake and vanishes at infinity. Location of the wake – indeed, its mere existence – has to be postulated (an example can be found in figure 2), but in order to remain consistent with the potential flow approximation, it has to start at the trailing edge. When the thickness of the body is vanishingly small – and it is small in the present model – ϕ can be identified with the scalar potential of the perturbation velocity (Wu 1971; Ashley & Landahl 1985).

Since the body is flat and of zero thickness, its footprint in a transverse (y–z) plane is the segment $( - s(x),s(x))$ of the y-axis by definition of the local reference frame (figures 2–4). The endpoints of this segment lay on the lower and upper edges of the body, respectively. On the forward part of the body, both edges face the flow (are ‘leading edges’); on the aft part of the body, the lower edge faces the flow, whereas the upper edge trails (figures 1–3). Starting at this trailing edge, the wake leaves a footprint only in a transverse plane crossing the aft part of the body. Its footprint starts at $y = s(x)$, but its shape is hardly simple (figure 3). It is reduced here to the segment $(s(x),1 - {y_0}(x))$ of the y-axis (figures 2–4) – an assumption that can be formally justified only when deviation of the actual footprint from the y-axis is small as compared with the length $s(0) - {y_0}(x) + s(x)$ of the body and wake together. This is perhaps the strongest assumption of the present theory, and its consequences will be demonstrated in § 8.

Figure 3. Footprints (shown in red) of the aft segment of the body and the wake in the transverse plane. Panels (a,c) show a typical (albeit exaggerated) combination of lateral and torsional deformation waves of an anguilliform swimmer. Panels (b,d) show a more benign case of a uniform (steady) twist. Panels (a,b) show a simplified wake as an extension of the body segment. Panels (c,d) show a more realistic wake shape where the vorticity is carried away from the trailing edge along the direction of the oncoming flow.

Figure 4. Footprints of the forward (a) and aft (b) segments in the transverse plane (such as the one shown in red on figure 2). The body occupies the segment $( - s(x),\;s(x))$ of the y-axis; it is shown in bold. The wake occupies the segment $(s(x),\;s(0) - {y_0}(x))$ of the y-axis; it is shown in red in (b). Solution domain is the (irrotational) exterior of the body and the wake.

Pertinent solution of the two-dimensional Laplace equation in an unbounded exterior of the segment (a, b) of the y-axis is

(3.1)\begin{equation}\phi (t,x,y,z) = \frac{1}{{2{\rm \pi}}}\int_a^b {\frac{{\mu (t,x,\zeta )z\,\textrm{d}\zeta }}{{{{(y - \zeta )}^2} + {z^2}}}} ,\end{equation}

where

(3.2)\begin{equation}\mu (t,x,y) = \phi (t,x,y, + 0) - \phi (t,x,y, - 0)\end{equation}

is the potential jump across it. Effectively, this is the potential of a distribution of z-axis-oriented doublets of intensity μ (Katz & Plotkin 1991). This general solution is yet to satisfy the impermeability condition

(3.3)\begin{equation}\mathop {\lim }\limits_{z \to \pm 0} \frac{{\partial \phi (t,x,y,z)}}{{\partial z}} ={-} w(t,x,y)\end{equation}

on the part of the segment containing the body (w will be defined shortly below), and no pressure jump condition

(3.4)\begin{equation}\frac{{\textrm{D}\mu ^{\prime}(t,x,y^{\prime})}}{{\textrm{D}t}} = 0\end{equation}

on the part of the segment containing the wake and the trailing edge. Here, $\textrm{D}/\textrm{D}t$ stands for the linearized Lagrangian derivative, $\partial /\partial t + \partial /\partial x$, and the prime with $\mu $ indicates its parametrization using coordinates of C′; recall that x and $x^{\prime}$are equivalent. When the motion of the body is limited to a combination of a lateral displacement and a rigid rotation, as was tacitly assumed in the first paragraph of § 2.1 and schematically shown in figures 2 and 3, the quantity on the right-hand side of (3.3) can be expressed as

(3.5)\begin{equation}w(t,x,y) = {w_0}(t,x) + {w_1}(t,x)y,\end{equation}

where

(3.6)\begin{gather}{w_0}(t,x) ={-} \frac{{\textrm{D}{z_0}(t,x)}}{{\textrm{D}t}} + \theta (t,x)\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}},\end{gather}

(3.7)\begin{gather}{w_1}(t,x) ={-} \frac{{\textrm{D}\theta (t,x)}}{{\textrm{D}t}};\end{gather}

details can be found in Appendix C of Part 1. Additional pair of conditions,

(3.8)\begin{gather}\mu (t,x, \pm s(x)) = 0\;\textrm{for}\;\textrm{each}\;x \in ({x_n},0),\end{gather}

(3.9)\begin{gather}\mu (t,x, - s(x)) = 0\;\textrm{for}\;\textrm{each}\;x \in (0,{x_t}),\end{gather}

manifest continuity of the velocity potential at the leading edges.

The conjunction of (3.1) and (3.3) furnishes two integro-differential equations for $\mu (t,x, \cdot )$, one for the forward segment, and one for the aft. The first one is

(3.10)\begin{equation}\frac{1}{{2{\rm \pi}}}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- s(x)}^{s(x)} \frac{{\partial \mu (t,x,\zeta )}}{{\partial \zeta }}\frac{{\textrm{d}\zeta }}{{y - \zeta }} = w(t,x,y)\end{equation}

for each $x \in ({x_n},0)$ and $y \in ( - s(x),s(x))$; the second one is

(3.11)\begin{equation}\frac{1}{{2{\rm \pi}}}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- s(x)}^{s(0) - {y_0}(x)} \frac{{\partial \mu (t,x,\zeta )}}{{\partial \zeta }}\frac{{\textrm{d}\zeta }}{{y - \zeta }} = w(t,x,y)\end{equation}

for each $x \in (0,{x_t})$ and $y \in ( - s(x),s(x))$. The difference between the two is in the integration limits. In both equations, the bar across the integral sign indicates the principal value in the Cauchy sense. The simplest way to obtain the expressions on the left of (3.10) and (3.11) is to integrate (3.1) by parts first, differentiate second and carefully pass to the limit. The passage to the limit introduces the principal value to the integral. In this form it appears in practically any textbook on aerodynamics (Katz & Plotkin 1991; Bisplinghoff, Ashley & Halfman 1996).

3.3. Post-processing

Solution of (3.10) can be found in Part 1 and it is briefly recapitulated in § 4 in a slightly different form; solution of (3.11), which turns out to be quite involved – in fact, it is the central contribution of this paper – can be found in § 5. Once solved, however, knowledge of $\partial \mu /\partial y$ and, consequently, of its first four moments,

(3.12)\begin{equation}{\mu _n}(t,x) = \frac{1}{{{s^{n + 1}}(x)}}\int_{ - s(x)}^{s(x)} {\frac{{\partial \mu (t,x,y)}}{{\partial y}}{y^n}\,\textrm{d}y} \end{equation}

(n being 0, 1, 2 or 3), suffices to obtain the suction force (per unit length) on the leading edges of the forward and aft segments,

(3.13)\begin{equation}{f_ \pm }(t,x) = \frac{\rm \pi}{4}{\left( {\mathop {\lim }\limits_{y \to \pm s(x)} \sqrt {s(x) \mp y} \frac{{\partial \mu (t,x,y)}}{{\partial y}}} \right)^2},\end{equation}

as well as all relevant moments

(3.14)\begin{equation}{\varPi _n}(t,x) ={-} \int_{ - s(x)}^{s(x)} {\Delta p(t,x,y){y^n}\,\textrm{d}y} \end{equation}

of the pressure jump

(3.15)\begin{equation}\Delta p(t,x,y) ={-} \frac{{\textrm{D}\mu ^{\prime}(t,x,y^{\prime})}}{{\textrm{D}t}} ={-} \frac{{\textrm{D}\mu (t,x,y)}}{{\textrm{D}t}} + \frac{{\partial \mu (t,x,y)}}{{\partial y}}\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}} + \ldots \end{equation}

across them. Equations (3.12)–(3.14) are (2.20), (2.36)–(2.37) and (2.32) of Part 1; (3.15) is a variant of (2.31) of Part 1; the ellipsis in (3.15) stands for the higher-order terms with respect to spatial and temporal derivatives of ${z_0}$, ${y_0}$ and θ. In turn, knowledge of the suction force and of the first three moments of pressure suffices to obtain the fluid-dynamic force (per unit length) acting on a cross-section of the body,

(3.16)\begin{equation}\boldsymbol{f}(t,x) ={-} \int_{ - s(x)}^{s(x)} {\Delta p(t,x,y)\boldsymbol{n}(t,x,y)\,\textrm{d}y + {f_ - }(t,x){\boldsymbol{n}_ - }(t,x) + {f_ + }(t,x){\boldsymbol{n}_ + }(t,x)} ;\end{equation}

the fluid-dynamic moment (per unit length) about the centre of that section,

(3.17)\begin{align} {\boldsymbol{m}_0}(t,x) & ={-} \int_{ - s(x)}^{s(x)} {\Delta p(t,x,y)(y{\boldsymbol{e}_{y^{\prime}}} + y\, \theta (t,x){\boldsymbol{e}_{z^{\prime}}}) \times \boldsymbol{n}(t,x,y)\,\textrm{d}y} \nonumber\\ & \quad + s(x)({\boldsymbol{e}_{y^{\prime}}} + \theta (t,x){\boldsymbol{e}_{z^{\prime}}}) \times ({f_ + }(t,x){\boldsymbol{n}_ + }(t,x) - {f_ - }(t,x){\boldsymbol{n}_ - }(t,x)); \end{align}

and the power (per unit length) needed to sustain the lateral motion of the body,

(3.18)\begin{equation}\iota (t,x) = \int_{ - s(x)}^{s(x)} {\Delta p(t,x,y)\frac{{\partial {z_b}(t,x,y)}}{{\partial t}}\,\textrm{d}y.}\end{equation}

In fact, using (3.14), the components of f and ${\boldsymbol{m}_0}$ can be recast as

(3.19)\begin{gather}{f_{x^{\prime}}}(t,x) ={-} \left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} - {\theta}(t,x)\dfrac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}} \right){\varPi}_{0}(t,x) - \dfrac{{\partial {\theta}(t,x)}}{{\partial x}}{\varPi _{1}}(t,x)\nonumber\\ \hspace{5.7pc}-\, \dfrac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}({f_{ +}}(t,x) - {f_{ - }}(t,x)) - \dfrac{{\textrm{d}s(x)}}{{\textrm{d}\kern0.06em x}}({f_{ + }}(t,x) + {f_{ -}}(t,x)),\end{gather}

(3.20)\begin{gather}{f_{y^{\prime}}}(t,x) ={-} \theta (t,x){\varPi _0}(t,x) + ({f_ + }(t,x) - {f_ - }(t,x)),\end{gather}

(3.21)\begin{gather}{f_{z^{\prime}}}(t,x) = {\varPi _0}(t,x),\end{gather}

(3.22)\begin{gather}{m_{0,x^{\prime}}}(t,x) = (1 + \theta (t,x)){\varPi _1}(t,x),\end{gather}

(3.23)\begin{gather}{m_{0,y^{\prime}}}(t,x) ={-} \theta (t,x){m_{0,z^{\prime}}}(t,x),\end{gather}

(3.24)\begin{gather} {m_{0,z^{\prime}}}(t,x) = \left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} - \theta (t,x)\dfrac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}} \right){\varPi _1}(t,x) + \dfrac{{\partial \theta (t,x)}}{{\partial x}}{\varPi _2}(t,x)\nonumber\\ \hspace{4pc} +\, s(x)({f_ + }(t,x) + {f_ - }(t,x))\left( {\theta (t,x)\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} + \dfrac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}} \right)\nonumber\\ \hspace{-2.2pc} -\, \dfrac{1}{2}({f_ + }(t,x) - {f_ - }(t,x))\dfrac{{\textrm{d}{s^2}(x)}}{{\textrm{d}\kern0.06em x}},\end{gather}

whereas

(3.25)\begin{equation}\iota (t,x) ={-} \frac{{\partial {z_0}(t,x)}}{{\partial t}}{\varPi _0}(t,x) - \frac{{\partial \theta (t,x)}}{{\partial t}}{\varPi _1}(t,x).\end{equation}

Details can be found in Part 1; (3.19)–(3.21) and (3.25) are variants of (3.3)–(3.5) and (3.21) of Part 1 with $|\theta |\ll 1$.

4. The forward segment

4.1. Potential jump and its moment

As mentioned already, a solution for the forward segment can be found in Part 1, and it remains unaffected by the presence of the aft segment. Being an inseparable part of the present solution, however, it is very briefly recapitulated below under the assumption that $|\theta |\ll 1$.

Equation (3.10) is solved using a variant of Söhngen (1939) inversion,

(4.1)\begin{equation}\frac{{\partial \mu (t,x,y)}}{{\partial y}} ={-} \frac{2}{\rm \pi}\frac{1}{{\sqrt {{s^2}(x) - {y^2}} }}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- s(x)}^{s(x)} \sqrt {{s^2}(x) - {\zeta ^2}} \frac{{w(t,x,\zeta )\,\textrm{d}\zeta }}{{y - \zeta }},\end{equation}

that prescribes square-root singularities of $\partial \mu /\partial y$ at $y ={\pm} s(x)$. This variant can be adapted from equation (5-66) in Ashley & Landahl (1985); a more general address can be found in Muskhelishvili (1953). The nth moment of $\partial \mu /\partial y$,

(4.2)\begin{equation}{\mu _n}(t,x) ={-} 2\int_{ - 1}^1 {\sqrt {1 - {\zeta ^2}} {A_n}(\zeta )w(t,x,\zeta s(x))\,\textrm{d}\zeta } ,\end{equation}

follows by (4.1) and (3.12) with

(4.3)\begin{equation}{A_n}(\zeta ) = \frac{1}{\rm \pi}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \frac{1}{{\sqrt {1 - {y^2}} }}\frac{{{y^n}\,\textrm{d}y}}{{y - \zeta }}.\end{equation}

It is shown in Appendix A that ${A_0}(\zeta )$ is zero for any $|\zeta |< 1$, and $- 1/\sqrt {{\zeta ^2} - 1}$ otherwise. It is also shown in Appendix A that subsequent functions satisfy the recurrence relation

(4.4)\begin{equation}{A_n}(\zeta ) = \sum\limits_{m = 0}^{n - 1} {{C_m}{\zeta ^{n - 1 - m}} + {A_0}(\zeta ){\zeta ^n}} ,\end{equation}

in which

(4.5)\begin{equation}{C_n} = \frac{1}{\rm \pi}\int_{ - 1}^1 {\frac{{{y^n}\,\textrm{d}y}}{{\sqrt {1 - {y^2}} }}} \end{equation}

are standard integrals. Among them, ${C_{2n + 1}}$ is zero for any non-negative integer n by symmetry considerations, whereas

(4.6)\begin{equation}{C_{2n}} = \frac{{(2n)!}}{{{2^{2n}}{{(n!)}^2}}}.\end{equation}

Noting that

(4.7)\begin{align}\int_{ - 1}^1 {\sqrt {1 - {\zeta ^2}} {A_n}(\zeta )\,\textrm{d}\zeta } &= \frac{1}{\rm \pi}\int_{ - 1}^1 {\sqrt {1 - {\zeta ^2}} \,\textrm{d}\zeta } \mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \frac{{{y^n}}}{{\sqrt {1 - {y^2}} }}\frac{{\textrm{d}y}}{{y - \zeta }}\nonumber\\ &= \int_{ - 1}^1 {\frac{{{y^{n + 1}}\,\textrm{d}y}}{{\sqrt {1 - {y^2}} }}} = {\rm \pi}{C_{n + 1}},\end{align}

(4.8)\begin{align}\int_{ - 1}^1 {\sqrt {1 - {\zeta ^2}} {A_n}(\zeta )\zeta \,\textrm{d}\zeta } &= \int_{ - 1}^1 {\frac{{{y^n}}}{{\sqrt {1 - {y^2}} }}\left( {{y^2} - \frac{1}{2}} \right)\,\textrm{d}y} = \frac{\rm \pi}{2}{C_n}\frac{n}{{n + 2}}\end{align}

by (4.3), (4.5) and (4.6), substitution of (3.5) in (4.2) furnishes

(4.9)\begin{gather}{\mu _{2n}}(t,x) ={-} {\rm \pi}{C_{2n}}\frac{n}{{n + 1}}{w_1}(t,x)s(x),\end{gather}

(4.10)\begin{gather}{\mu _{2n + 1}}(t,x) ={-} 2{\rm \pi}{C_{2n + 2}}{w_0}(t,x).\end{gather}

4.2. Moments of the pressure jump

The nth moment of pressure,

(4.11)\begin{equation}{\varPi _n}(t,x) = \int_{ - s(x)}^{s(x)} {\left( {\frac{{\textrm{D}\mu (t,x,y)}}{{Dt}} - \frac{{\partial \mu (t,x,y)}}{{\partial y}}\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}} \right){y^n}\,\textrm{d}y} ,\end{equation}

follows by (3.14) and (3.15). Because, on the forward segment, the potential jump vanishes at both edges by (3.8), the convective derivative in the first term can be taken outside the integral sign; followed by integration by parts it yields

(4.12)\begin{equation}{\varPi _n}(t,x) ={-} \frac{1}{{n + 1}}\frac{\textrm{D}}{{\textrm{D}t}}({s^{n + 2}}(x){\mu _{n + 1}}(x)) - \frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}{s^{n + 1}}(x){\mu _n}(x)\end{equation}

by (3.12). Consequently,

(4.13)\begin{gather}{\varPi _{2n}}(t,x) = \frac{{2{\rm \pi}{C_{2n + 2}}}}{{2n + 1}}\frac{\textrm{D}}{{\textrm{D}t}}({s^{2n + 2}}(x){w_0}(t,x)) + \frac{{{\rm \pi} n{C_{2n}}}}{{n + 1}}\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}{s^{2n + 2}}(x){w_1}(t,x),\end{gather}

(4.14)\begin{gather}{\varPi _{2n + 1}}(t,x) = \frac{{{\rm \pi} {C_{2n + 2}}}}{{2(n + 2)}}\frac{\textrm{D}}{{\textrm{D}t}}({s^{2n + 4}}(x){w_1}(t,x)) + 2{\rm \pi}{C_{2n + 2}}\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}{s^{2n + 2}}(x){w_0}(t,x)\end{gather}

by (4.9) and (4.10).

4.3. Leading-edge suction

Suction force on the upper (‘+’) and lower (‘−’) edges of the forward segment is given by

(4.15)\begin{equation}{f_ \pm }(t,x) = \frac{\rm \pi}{4}A_ \pm ^2(t,x),\end{equation}

where

(4.16)\begin{equation}{A_ \pm }(t,x) = \mathop {\lim }\limits_{y \to \pm s(x)} \left( {\sqrt {s(x) \mp y} \frac{{\partial \mu (t,x,y)}}{{\partial y}}} \right)\end{equation}

is the coefficient with the square-root singularity of $\mu $ at the respective edge. This pair of equations comes instead of (3.13). Equation (4.16) yields

(4.17)\begin{equation}{A_ \pm }(t,x) ={\mp} \frac{2}{\rm \pi}\frac{1}{{\sqrt {2s(x)} }}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- s(x)}^{s(x)} \sqrt {\frac{{s(x) \pm \zeta }}{{s(x) \mp \zeta }}} w(t,x,\zeta )\,\textrm{d}\zeta \end{equation}

by (4.1), from which

(4.18)\begin{equation}{A_ \pm }(t,x) ={\mp} \sqrt {2s(x)} \left( {{w_0}(t,x) \pm \frac{1}{2}{w_1}(t,x)s(x)} \right)\end{equation}

follows by (3.5). Thus,

(4.19)\begin{equation}{f_ \pm }(t,x) = \frac{\rm \pi}{2}s(x){\left( {{w_0}(t,x) \pm \frac{1}{2}{w_1}(t,x)s(x)} \right)^2}\end{equation}

by (4.15).

4.4. Sectional force, moment and power

Introducing (4.19), (4.13), (4.14) and (4.6) in (3.19)–(3.25) yields

(4.20)\begin{gather}{f_x}(t,x) ={-} {\rm \pi}\dfrac{\textrm{D}}{{\textrm{D}t}}\left( {{s^2}(x){w_0}(t,x)\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} - \theta (t,x)\dfrac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}} \right) + \dfrac{{{s^4}(x)}}{8}{w_1}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial x}}} \right)\nonumber\\ \quad -\, \dfrac{\rm \pi}{2}\dfrac{\partial }{{\partial x}}\left( {{s^2}(x)w_0^2(t,x) + \dfrac{1}{8}{s^4}(x)w_1^2(t,x)} \right),\end{gather}

(4.21)\begin{gather}{f_{y^{\prime}}}(t,x) ={-} {\rm \pi}\frac{\textrm{D}}{{\textrm{D}t}}({s^2}(x){w_0}(t,x)\theta (t,x)),\end{gather}

(4.22)\begin{gather}{f_{z^{\prime}}}(t,x) = {\rm \pi}\frac{\textrm{D}}{{\textrm{D}t}}({s^2}(x){w_0}(t,x)),\end{gather}

(4.23)\begin{gather}\iota (t,x) ={-} {\rm \pi}\dfrac{\textrm{D}}{{\textrm{D}t}}\left( {{s^2}(x){w_0}(t,x)\dfrac{{\partial {z_0}(t,x)}}{{\partial t}} + \dfrac{1}{8}{s^4}(x){w_1}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial t}}} \right)\nonumber\\ \quad -\, \dfrac{\rm \pi}{2}\dfrac{\partial }{{\partial t}}\left( {{s^2}(x)w_0^2(t,x) + \dfrac{1}{8}{s^4}(x)w_1^2(t,x)} \right). \end{gather}

Essentially, these are variants of (3.9), (3.7), (3.8) and (3.23) of Part 1 under the assumption that the twist angle θ is small as compared with unity. Under the same assumption,

(4.24)\begin{equation}{m_{0,x}}(t,x) = \frac{\rm \pi}{8}\frac{\textrm{D}}{{\textrm{D}t}}({s^4}(x){w_1}(t,x)) + {\rm \pi}{s^2}(x){w_0}(t,x)\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}\end{equation}

by (3.22) and (4.14); the remaining two components of ${\boldsymbol{m}_0}$, ${m_{0,y^{\prime}}}$ and ${m_{0,z^{\prime}}}$, are rendered insignificant in § 6, and hence are not shown.

5. The aft segment

5.1. Boundary integral equation

The potential jump across the aft segment of the body is governed by (3.11), which has to be satisfied for each $x \in (0,{x_t})$ and $y \in ( - s(x),s(x))$. Separating the part of the integration interval containing the wake, it can be re-written as

(5.1)\begin{equation}\frac{1}{{2{\rm \pi}}}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- s(x)}^{s(x)} \frac{{\partial \mu (t,x,\zeta )}}{{\partial \zeta }}\frac{{\textrm{d}\zeta }}{{y - \zeta }} = w(t,x,y) - \frac{1}{{2{\rm \pi}}}\int_{s(x)}^{s(0) - {y_0}(x)} {\frac{{\partial \mu (t,x,\zeta )}}{{\partial \zeta }}\frac{{\textrm{d}\zeta }}{{y - \zeta }}} .\end{equation}

This move anticipates subsequent substitution of (3.4) for the potential jump across the wake. Because $\mu ^{\prime}(t,x,y^{\prime}) = \mu (t,x,y^{\prime} - {y_0}(x)) = \mu (t,x,y)$ by (2.4) and (2.5), (3.4) actually implies that for any point $(x,y)$ of the wake with $x \in (0,{x_t})$ and $y \in (s(x),s(0) - {y_0}(x))$,

(5.2)\begin{equation}\mu (t,x,y) = \mu (t - (x - {x_ + }(x,y)),{x_ + }(x,y),s({x_ + }(x,y))),\end{equation}

where ${x_ + }(x,y)$ is the point of the trailing edge that has the same $y^{\prime}$ coordinate as the point of the wake, i.e. it is the solution of

(5.3)\begin{equation}{y_0}({x_ + }) + s({x_ + }) = y + {y_0}(x),\end{equation}

whereas $\mu (t,x,s(x))$ is the value of the potential jump at the trailing edge of the aft segment (Wu 1971; Yates 1983). Consequently, for any point of the wake,

(5.4)\begin{equation}\frac{{\partial \mu (t,x,\zeta )}}{{\partial \zeta }} = {\left( {\frac{{\partial \mu (t^{\prime\prime},x^{\prime\prime},s(x^{\prime\prime}))}}{{\partial t^{\prime\prime}}} + \frac{{\partial \mu (t^{\prime\prime},x^{\prime\prime},s(x^{\prime\prime}))}}{{\partial x^{\prime\prime}}}} \right)_{\scriptstyle t^{\prime\prime} = t - (x - {x_ + }(x,\zeta )) \atop \scriptstyle x^{\prime\prime} = {x_ + }(x,\zeta ) }}\frac{{\partial {x_ + }(x,\zeta )}}{{\partial \zeta }}.\end{equation}

This relation allows changing of the integration variable in (5.1) to ${x_ + }$, which leads to

(5.5)\begin{align} \dfrac{1}{{2{\rm \pi}}}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- s(x)}^{s(x)} \dfrac{{\partial \mu (t,x,\zeta )}}{{\partial \zeta }}\dfrac{{\textrm{d}\zeta }}{{y - \zeta }} &= w(t,x,y)\nonumber\\ & \quad + \dfrac{1}{{2{\rm \pi}}}\int_0^x {\dfrac{{{{\left( {\dfrac{{\partial \mu (t^{\prime\prime},x^{\prime\prime},s(x^{\prime\prime}))}}{{\partial t^{\prime\prime}}} + \dfrac{{\partial \mu (t^{\prime\prime},x^{\prime\prime},s(x^{\prime\prime}))}}{{\partial x^{\prime\prime}}}} \right)}_{\scriptstyle t^{\prime\prime} = t - (x - {x_ + }) \atop \scriptstyle x^{\prime\prime} = {x_ + } }}\,\textrm{d}{x_ + }}}{{y + {y_0}(x) - ({y_0}({x_ + }) + s({x_ + }))}};} \end{align}

the change in sign comes from exchanging the upper and lower integration limits: $y = s(x)$ corresponds to ${x_ + } = x$, whereas $y = s(0) - {y_0}(x)$ corresponds to ${x_ + } = 0$, both by (5.3).

Equation (5.5) has no analytical solution in the general case. At the same time, its numerical solution (e.g. Baddoo, Hajian & Jaworski 2021) renders the slender body approximation redundant. There is hardly any benefit in attempting a numerical solution of an approximate model in the framework of the potential flow theory, when a fast numerical solution of the exact model in the framework of the same theory is readily available (Appendix H). Fortuitously, when the projection of the aft part of the body on the x–y plane has straight and parallel edges, as in figures 1–3, i.e. when

(5.6)\begin{gather}{y_0}(x) ={-} x\tan \lambda ,\end{gather}

(5.7)\begin{gather}s(x) = s(0) = 1 \end{gather}

for each $x \in (0,{x_t})$, (5.5) takes on a much simpler form,

(5.8) \begin{align}\frac{1}{{2{\rm \pi}}}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \frac{{\partial \mu (t,x,\zeta )}}{{\partial \zeta }}\frac{{\textrm{d}\zeta }}{{y \!-\! \zeta }} &= w(t,x,y)\nonumber\\ &\quad + \dfrac{1}{{2{\rm \pi}}}\int_0^x {\dfrac{{{{\left( {\dfrac{{\partial \mu (t^{\prime\prime},x^{\prime\prime},1)}}{{\partial t^{\prime\prime}}} \!+\! \dfrac{{\partial \mu (t^{\prime\prime},x^{\prime\prime},1)}}{{\partial x^{\prime\prime}}}} \right)}_{\scriptstyle t^{\prime\prime} = t - (x - {x_ + }) \atop \scriptstyle x^{\prime\prime} = {x_ + } }}\,\textrm{d}{x_ + }}}{{(y - 1) - (x - {x_ + })\tan \lambda }},}\end{align}

which is tractable analytically. It is solved in the next section. Although $\lambda $ is a small quantity by assumption, $\tan \lambda $ will not be replaced by $\lambda $ to facilitate tracking. The reader is reminded that $\lambda $ was assumed in § 2.1 to be strictly positive.

5.2. Potential jump and its moments

We begin by applying a pair of Laplace transforms to (5.8): one,

(5.9)\begin{equation}L\{ f({\cdot} , \ldots );q\} = \int_0^\infty {f(t, \ldots )\,{\textrm{e}^{ - qt}}\,\textrm{d}t} ,\end{equation}

with respect to time (here, f is an arbitrary function, q is the Laplace variable and the ellipsis is a placeholder for possible additional arguments of f), and the other,

(5.10)\begin{equation}L\{ f({\sim} ,\cdot , \ldots );p\} = \int_0^\infty {f({\sim} ,x, \ldots )\,{\textrm{e}^{ - px}}\,\textrm{d}\kern0.06em x} ,\end{equation}

with respect to x (p stands for another Laplace variable, and the tilde is a placeholder for time or for the associated Laplace variable). It is agreed that a function receives a hat after the ‘time’ transform (and time transform only), an inverted hat after the ‘space’ transform (and space transform only) and a tilde-like hat after the two of them. Assuming, with no loss of generality, that the body causes no perturbation to the oncoming flow prior to time $t = 0$ – and hence both $w(t,x,y)$ and $\mu (t,x,y)$ are zero for any $t < 0$ and any point along the body – the outcome of these two transforms is

(5.11)\begin{equation}\frac{1}{{2{\rm \pi}}}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \frac{{\partial \tilde{\mu }(q,p,y^{\prime})}}{{\partial y^{\prime}}}\frac{{\textrm{d}y^{\prime}}}{{y - y^{\prime}}} = \tilde{w}(q,p,y) + \frac{{\kappa {\textrm{e}^\kappa }}}{{2{\rm \pi}}}\tilde{\mu }(q,p,1)\int_1^\infty {\frac{{{\textrm{e}^{ - \kappa y^{\prime}}}\,\textrm{d}y^{\prime}}}{{y - y^{\prime}}}} ,\end{equation}

in which

(5.12)\begin{equation}\kappa = (p + q)\cot \lambda ;\end{equation}

details can be found in Appendix B. Equation (5.11) has to be satisfied for every $y \in ( - 1,1)$.

Equation (5.11) is essentially the same as the one appearing in the theory of oscillating wing sections (Bisplinghoff et al. 1996), and is solved here by following exactly the same steps. Starting with the Söhngen (1939) inversion, it becomes

(5.13)\begin{align}\frac{{\partial \tilde{\mu }(q,p,y)}}{{\partial y}} &={-} \frac{2}{\rm \pi}\sqrt {\frac{{1 \!-\! y}}{{1 \!+\! y}}}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \sqrt {\frac{{1 \!+\! \zeta }}{{1 \!-\! \zeta }}} \frac{{\textrm{d}\zeta }}{{y \!-\! \zeta }}\nonumber\\ &\quad \times\left( {\tilde{w}(q,p,\zeta ) \!+\! \frac{{\kappa {\textrm{e}^\kappa }\tilde{\mu }(q,p,1)}}{{2{\rm \pi}}}\int_1^\infty {\frac{{{\textrm{e}^{ - \kappa y^{\prime}}}\,\textrm{d}y^{\prime}}}{{\zeta \!-\! y^{\prime}}}} } \right).\end{align}

This particular variant of the inversion is the same as in the theory of wing sections (Ashley & Landahl 1985; Bisplinghoff et al. 1996), but different for the one used for the forward segment – here, it prescribes a square-root singularity of $\partial \tilde{\mu }/\partial y$ at the leading edge $(y ={-} 1)$ and no singularity at the trailing edge $(y = 1)$. Evaluating the integral with respect to $\zeta $ in the last term furnishes (5.13) in somewhat simpler form,

(5.14)\begin{align} \frac{{\partial \tilde{\mu }(q,p,y)}}{{\partial y}} &= \sqrt {\frac{{1 - y}}{{1 + y}}} \left( - \frac{2}{\rm \pi}\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \sqrt {\frac{{1 + \zeta }}{{1 - \zeta }}} \frac{{\tilde{w}(q,p,\zeta )\,\textrm{d}\zeta }}{{y - \zeta }} \right. \nonumber\\ &\quad\left. +\, \frac{{\kappa {\textrm{e}^\kappa }\tilde{\mu }(q,p,1)}}{\rm \pi}\int_1^\infty {\sqrt {\frac{{y^{\prime} + 1}}{{y^{\prime} - 1}}} \frac{{{\textrm{e}^{ - \kappa y^{\prime}}}\,\textrm{d}y^{\prime}}}{{y - y^{\prime}}}} \right),\end{align}

which is the one to be used below.

Bearing in mind that $\tilde{\mu }(q,p, - 1) = 0$ by (3.9), (5.14) can be integrated on both sides with respect to y between −1 and 1 to obtain an algebraic equation

(5.15)\begin{align}\tilde{\mu }(q,p,1) = 2\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \sqrt {\frac{{1 + \zeta }}{{1 - \zeta }}}\, \tilde{w}(q,p,\zeta )\,\textrm{d}\zeta - \kappa {\textrm{e}^\kappa }\tilde{\mu }(q,p,1)\int_1^\infty {\left( {\sqrt {\frac{{y^{\prime} + 1}}{{y^{\prime} - 1}}} - 1} \right)\,{\textrm{e}^{ - \kappa y^{\prime}}}\,\textrm{d}y^{\prime}} \end{align}

for $\tilde{\mu }(q,p,1)$. The last term on the right (containing $\int_1^\infty {{\textrm{e}^{ - \kappa y^{\prime}}}\,\textrm{d}y^{\prime}} $) cancels out with the term on the left; the second term from the right (containing $\int_1^\infty {\sqrt {(y^{\prime} + 1)/(y^{\prime} - 1)} \,{\textrm{e}^{ - \kappa y^{\prime}}}\,\textrm{d}y^{\prime}}$) is identified with the combination ${{\rm K}_0}(\kappa ) + {{\rm K}_1}(\kappa )$ of Bessel functions; what is left, reduces to

(5.16)\begin{equation}\tilde{\mu }(q,p,1) = 2 {\tilde{\varPhi }}_0^{(0)}(\kappa )\mathop {\rlap{-{-}}{\!\int }}\nolimits_{\!\!\!\!- 1}^1 \sqrt {\frac{{1 + \zeta }}{{1 - \zeta }}}\, \tilde{w}(q,p,\zeta )\,\textrm{d}\zeta ,\end{equation}

where

(5.17)\begin{equation}\tilde{\varPhi }_k^{(0)}(\kappa ) = \frac{1}{{{\kappa ^{k + 1}}\,{\textrm{e}^\kappa }({{\rm K}_0}(\kappa ) + {{\rm K}_1}(\kappa ))}}\end{equation}

is the Laplace transform of the kth-order Küssner function (Sears 1940; Iosilevskii 2007, 2012). The proper Küssner function – the one representing the lift response of a wing section to a sharp-edged gust, or the potential jump at the trailing edge due to a step in the angle of attack – is of the first order. The purpose of the superscript with ${\tilde{\varPhi }_k}$ will become clear shortly.

By definition, $\tilde{\mu }(q,p,1)$ is also the zeroth-order moment ${\tilde{\mu }_0}(q,p)$ of $\partial \tilde{\mu }(q,p,y)/\partial y$ – exactly as $\mu (t,x,1)$ is the zeroth-order moment ${\mu _0}(t,x)$ of $\partial \mu (t,x,y)/\partial y$ by (3.12) and (5.7). In general, however, the nth moment of $\partial \tilde{\mu }(q,p,y)/\partial y$,

(5.18)\begin{equation}{\tilde{\mu }_n}(q,p) = \int_{ - 1}^1 {\frac{{\partial \tilde{\mu }(q,p,y)}}{{\partial y}}{y^n}\,\textrm{d}y} ,\end{equation}

is given by

(5.19)\begin{align} {{\tilde{\mu }}_n}(q,p) & ={-} 2\int_{ - 1}^1 {\sqrt {\dfrac{{1 + \zeta }}{{1 - \zeta }}}\, \tilde{w}(q,p,\zeta )({A_n}(\zeta ) - {A_{n + 1}}(\zeta ))\,\textrm{d}\zeta } \nonumber\\ & \quad + \kappa {\textrm{e}^\kappa }\tilde{\mu }(q,p,1)\int_1^\infty {\sqrt {\dfrac{{y^{\prime} + 1}}{{y^{\prime} - 1}}} {\textrm{e}^{ - \kappa y^{\prime}}}({A_n}(y^{\prime}) - {A_{n + 1}}(y^{\prime}))\,\textrm{d}y^{\prime}} ; \end{align}

this particular form follows (5.18) by (5.14) and (4.3). Further reduction of this equation is quite bulky, but can be found in full in Appendix C. Eventually, it yields

(5.20)\begin{gather}{\tilde{\mu }_{2n}}(q,p) ={-} {\rm \pi}{\tilde{w}_1}(q,p)\frac{{n{C_{2n}}}}{{n + 1}} + 2{\rm \pi}\tilde{\varPhi }_0^{(2n)}(\kappa ){\tilde{w}_{3/4}}(q,p),\end{gather}

(5.21)\begin{gather}{\tilde{\mu }_{2n + 1}}(q,p) ={-} 2{\rm \pi}{\tilde{w}_0}(q,p){C_{2n + 2}} + 2{\rm \pi}\tilde{\varPhi }_0^{(2n + 1)}(\kappa ){\tilde{w}_{3/4}}(q,p),\end{gather}

where, for each n > 0,

(5.22)\begin{equation}\tilde{\varPhi }_k^{(n)}(\kappa ) = \frac{{{{( - 1)}^n}}}{{{\kappa ^k}({{{\rm K}_0}(\kappa ) + {{\rm K}_1}(\kappa )} )}}\left( {\frac{{{\textrm{d}^n}}}{{\textrm{d}{\kappa^n}}}\frac{{{\textrm{e}^{ - \kappa }}}}{\kappa } + \sum\limits_{m = 0}^{floor((n - 1)/2)} {{C_{2m}}} \frac{{{\textrm{d}^{n - 1 - 2m}}}}{{\textrm{d}{\kappa^{n - 1 - 2m}}}}\frac{{{{\rm K}_1}(\kappa )}}{\kappa }} \right)\end{equation}

is an ad hoc combination of Bessel and exponential functions, whereas

(5.23)\begin{equation}{\tilde{w}_{3/4}}(q,p) = {\tilde{w}_0}({q,p} )+ (1/2){\tilde{w}_1}(q,p)\end{equation}

can be interpreted as the double transform of the velocity normal to the body at the respective three-quarter chord point,

(5.24)\begin{equation}{w_{3/4}}(t,x) = {w_0}(t,x) + (1/2){w_1}(t,x);\end{equation}

see (3.5).

Now, let

(5.25)\begin{equation}\varPhi _k^{(n)}(x) = {L^{ - 1}}\{ \tilde{\varPhi }_k^{(n)};x\} = \frac{1}{{2{\rm \pi} \mathrm{i}}}\int_{Br} {\tilde{\varPhi }_k^{(n)}\textrm{(}\kappa \textrm{)}\,{\textrm{e}^{\kappa x}}\,\textrm{d}\kappa } \end{equation}

be the inverse transform of $\tilde{\varPhi }_k^{(n)}$; Br is the Bromwich contour. When $\kappa \to \infty $, ${{\rm K}_0}(\kappa )$, ${{\rm K}_1}(\kappa )$ and their derivatives of any order with respect to $\kappa $ behave as ${\textrm{e}^{ - \kappa }}/\sqrt \kappa $, and, consequently, $\tilde{\varPhi }_k^{(n)}(\kappa ) = O(\sqrt \kappa /{\kappa ^{k + 1}})$ by (5.22). Consequently, for any $n \ge 0$,

(5.26)\begin{equation}\varPhi _k^{(n)}(0) = 0\end{equation}

when $k > 0$, but has a square-root singularity when $k = 0$. Moreover, for any $x > 0$,

(5.27)\begin{equation}\varPhi _0^{(n)}(x) = \textrm{d}\varPhi _1^{(n)}(x)/\textrm{d}\kern0.06em x.\end{equation}

With these, the pair of inverse transforms in (5.20) and (5.21) furnish

(5.28)\begin{gather}{\mu _{2n}}(t,x) ={-} {\rm \pi}{w_1}(t,x)\frac{{n{C_{2n}}}}{{n + 1}} + 2{\rm \pi}\tan \lambda \int_0^{{x_{\ast} }} {\varPhi _0^{({2n} )}(x^{\prime}\tan \lambda ){w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}} ,\end{gather}

(5.29)\begin{gather}{\mu _{2n + 1}}(t,x) ={-} 2{\rm \pi}{w_0}(t,x){C_{2n + 2}} + 2{\rm \pi}\tan \lambda \int_0^{{x_{\ast} }} {\varPhi _0^{(2n + 1)}(x^{\prime}\tan \lambda ){w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}} ,\end{gather}

where

(5.30)\begin{equation}{x_{\ast} } = \min (t,x);\end{equation}

details can be found in Appendix E. In view of (5.26) and (5.27), their alternative forms are

(5.31)\begin{align}{\mu _{2n}}(t,x) & ={-} {\rm \pi}{C_{2n}}\dfrac{n}{{n + 1}}{w_1}(t,x) + 2{\rm \pi}\varPhi _1^{(2n)}({x_{\ast} }\tan \lambda ){w_{3/4}}(t - {x_{\ast} },x - {x_{\ast} })\nonumber\\ & \quad + 2{\rm \pi}\int_0^{{x_{\ast} }} {\varPhi _1^{({2n} )}(x^{\prime}\tan \lambda )} \dfrac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}, \end{align}

(5.32)\begin{align}{\mu _{2n + 1}}(t,x) & ={-} 2{\rm \pi}{C_{2n + 2}}{w_0}(t,x) + 2{\rm \pi} \varPhi_1^{(2n + 1)}({x_{\ast} }\tan \lambda ){w_{3/4}}(t - {x_{\ast} },x - {x_{\ast} })\nonumber\\ & \quad + 2{\rm \pi}\int_0^{{x_{\ast} }} {{\varPhi }_1^{(2n + 1)}(x^{\prime}\tan \lambda )} \dfrac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}.\end{align}

5.3. Moments of the pressure jump

The nth moment of the pressure jump on the aft segment is related to the potential jump by the same expression as on the forward one, (4.11). In the present case, however, the potential jump does not vanish at the trailing edge, but constancy of the integration limits still allows for use of the same sequence of operations as on the forward segment. Thus,

(5.33)\begin{align} {\varPi _n}(t,x) & = \int_{ - 1}^1 {\left( {\dfrac{{\textrm{D}\mu (t,x, - x\tan \lambda + y)}}{{\textrm{D}t}} + \dfrac{{\partial \mu (t,x, - x\tan \lambda + y)}}{{\partial y}}\tan \lambda } \right){y^n}\,\textrm{d}y} \nonumber\\ & = \dfrac{1}{{n + 1}}\dfrac{\textrm{D}}{{\textrm{D}t}}({\mu _0}(t,x) - {\mu _{n + 1}}(t,x)) + \tan \lambda {\mu _n}(t,x)\end{align}

by (4.12), (5.6) and (5.7). Introducing (5.28)–(5.32), it becomes

(5.34)\begin{align} {\varPi_{2n}}(t,x) & = 2{\rm \pi}\dfrac{{{C_{2n + 2}}}} {{2n + 1}}\dfrac{{\textrm{D}{w_0}(t,x)}}{{\textrm{D}t}} - {\rm \pi}\tan \lambda\, {w_1}(t,x)\dfrac{{n{C_{2n}}}}{{n + 1}}\nonumber\\ & \quad + 2{\rm \pi}\tan \lambda \left(\vphantom{\left. \quad + \int_0^{{x_{\ast} }} {{G_{2n + 1}}(x^{\prime}\tan \lambda )} \dfrac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime} \right)}{G_{2n}}({x_{\ast} }\tan \lambda ){w_{3/4}}(t - {x_{\ast} },x - {x_{\ast} }) \right.\nonumber\\ & \left.\quad + \int_0^{{x_{\ast}}} {{G_{2n}}(x^{\prime}\tan \lambda )} {\dfrac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}} \right), \end{align}

(5.35)\begin{align} {\varPi _{2n + 1}}(t,x) & = \dfrac{\rm \pi}{2}\dfrac{{{C_{2n + 2}}}}{{n + 2}}\dfrac{{\textrm{D}{w_1}(t,x)}}{{\textrm{D}t}} - 2{\rm \pi}\tan \lambda\, {w_0}(t,x){C_{2n + 2}}\nonumber\\ & \quad + 2{\rm \pi}\tan \lambda \left(\vphantom{\left. \quad + \int_0^{{x_{\ast} }} {{G_{2n + 1}}(x^{\prime}\tan \lambda )} \dfrac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime} \right)}{{G_{2n + 1}}({x_{\ast} }\tan \lambda ){w_{3/4}}(t - {x_{\ast} },x - {x_{\ast} })} \right.\nonumber\\ &\left. \quad + \int_0^{{x_{\ast} }} {{G_{2n + 1}}(x^{\prime}\tan \lambda )} \dfrac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime} \right), \end{align}

where ${G_n}$ stands for the combination

(5.36)\begin{equation}{G_n}(x) = \frac{1}{{n + 1}}\varPhi _0^{(0)}(x) - \frac{1}{{n + 1}}\varPhi _0^{(n + 1)}(x) + \varPhi _1^{(n)}(x)\end{equation}

of functions $\varPhi _m^{(n)}$, which were defined in (5.22) and (5.25).

Remarkably, the Laplace transform of ${G_n}$ reduces to

(5.37)\begin{gather}{\tilde{G}_{2n}}(\kappa ) = \frac{{{C_{2n}}}}{{{{\rm K}_0}(\kappa ) + {{\rm K}_1}(\kappa )}}\frac{{{{\rm K}_1}(\kappa )}}{\kappa } = {C_{2n}}{\tilde{\varPsi }_1}(\kappa ),\end{gather}

(5.38)\begin{gather}{\tilde{G}_{2n - 1}}(\kappa ) = \frac{{{C_{2n}}}}{{{{\rm K}_0}(\kappa ) + {{\rm K}_1}(\kappa )}}\frac{{{{\rm K}_0}(\kappa )}}{\kappa } = {C_{2n}}\left( {\frac{1}{\kappa } - {{\tilde{\varPsi }}_1}(\kappa )} \right),\end{gather}

where

(5.39)\begin{equation}{\tilde{\varPsi }_k}(\kappa ) = \frac{1}{{{\kappa ^k}}}\frac{{{{\rm K}_1}(\kappa )}}{{{{\rm K}_0}(\kappa ) + {{\rm K}_1}(\kappa )}}\end{equation}

is identified with the Laplace transform of the kth-order Wagner function ${\varPsi _k}$ (Sears 1940; Iosilevskii 2007). Consequently,

(5.40)\begin{gather}{G_{2n}}(x) = {C_{2n}}{\varPsi _1}(x),\end{gather}

(5.41)\begin{gather}{G_{2n - 1}}(x) = {C_{2n}}({\rm H}(x) - {\varPsi _1}(x)),\end{gather}

where ${\tilde{\varPsi }_k}(\kappa )$ behaves as $(1/2 + 1/8\kappa + \ldots )(1/{\kappa ^k})$ when $\kappa \to \infty $, and therefore ${\varPsi _0}$ behaves at the origin as a combination of a delta function $\delta$ and a step H; ${\varPsi _1}$ (this is the proper Wagner function) behaves as a step with ${\varPsi _1}( + 0) = 1/2$; all higher-order functions properly vanish. To avoid ambiguity hereafter, it will be agreed that

(5.42)\begin{equation}{\varPsi _k}(0) = 0\end{equation}

for any $k \ge 0$, and, under this assumption,

(5.43)\begin{equation}{\varPsi _{k - 1}}(x) = \textrm{d}{\varPsi _k}(x)/\textrm{d}\kern0.06em x\end{equation}

for any k > 0. Rational approximations for ${\varPsi _0},{\varPsi _1}, \ldots $ can be found in Appendix F.

Using (5.40) and (5.41), equations (5.34) and (5.35) for the pressure moments can be recast as

(5.44)\begin{align} {\varPi _{2n}}(t,x) & = \dfrac{{{\rm \pi}{C_{2n}}}}{{n + 1}}\left( {\dfrac{{\textrm{D}{w_0}(t,x)}}{{\textrm{D}t}} + \tan \lambda {w_1}(t,x)} \right)\nonumber\\ & \quad - {\rm \pi}{C_{2n}}\tan \lambda ({w_1}(t,x) - 2{W_{3/4}}(t,x,\tan \lambda )), \end{align}

(5.45)\begin{align}{\varPi _{2n + 1}}(t,x) &= \frac{1}{2}\frac{{{\rm \pi}{C_{2n + 2}}}}{{n + 2}}\frac{{\textrm{D}{w_1}(t,x)}}{{\textrm{D}t}} + {\rm \pi}{C_{2n + 2}}\tan \lambda ({w_1}(t,x) - 2{W_{3/4}}(t,x,\tan \lambda )),\end{align}

where

(5.46)\begin{align} {W_{3/4}}(t,x,\tan \lambda ) & = {\varPsi _1}({x_{\ast} }\tan \lambda ){w_{3/4}}(t - {x_{\ast} },x - {x_{\ast} })\nonumber\\ & \quad + \int_0^{{x_{\ast} }} {{\varPsi _1}(x^{\prime}\tan \lambda )} \dfrac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime} \end{align}

embodies the contribution of the wake. It manifests the dependence of the pressure moments on the history of the wing's motion. When writing (5.44), equation (4.6) was used to relate ${C_{2n + 2}}$ and ${C_{2n}}$. Since

(5.47)\begin{equation}\frac{\textrm{D}}{{\textrm{D}t}}{w_{3/4}}(t - x^{\prime},x - x^{\prime}) ={-} \frac{\textrm{d}}{{\textrm{d}\kern0.06em x^{\prime}}}{w_{3/4}}(t - x^{\prime},x - x^{\prime}),\end{equation}

the last term on the right-hand side of (5.46) can be integrated by parts to obtain

(5.48)\begin{equation}{W_{3/4}}(t,x,\tan \lambda ) = \tan \lambda \int_0^{{x_{\ast} }} {{\varPsi _\textrm{0}}(x^{\prime}\tan \lambda ){w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}} ;\end{equation}

note the delta-function content of ${\varPsi _0}$ at the origin, as well as equations (5.42) and (5.43).

5.4. Leading-edge suction

Suction force works only on the lower (leading) edge of the aft segment. Essentially, it is given by the same pair of equations as on the forward one ((4.15) and (4.16)), but lacking a closed form expression for the potential jump in the time domain, finding the coefficient

(5.49)\begin{equation}{A_ - }(t,x) = \mathop {\lim }\limits_{y \to - 1} \left( {\sqrt {1 + y} \frac{{\partial \mu (t,x,y)}}{{\partial y}}} \right)\end{equation}

with the square-root singularity at the leading edge becomes more involved. A possible solution here is to apply the pair of Laplace transforms (one with respect to time and the other with respect to x), exploit (5.14) and bring the expression back to physical variables. In this case, the pair of Laplace transforms yields

(5.50)\begin{equation}{\tilde{A}_ - }(q,p) = \mathop {\lim }\limits_{y \to - 1} \left(\sqrt {1 + y} \frac{{\partial \tilde{\mu }(q,p,y)}}{{\partial y}}\right),\end{equation}

from which

(5.51)\begin{equation}{\tilde{A}_ - }(q,p) = \frac{{\sqrt 2 }}{\rm \pi}\left( {2\int_{ - 1}^1 {\frac{{\tilde{w}(q,p,\zeta )\,\textrm{d}\zeta }}{{\sqrt {1 - {\zeta^2}} }}} - \tilde{\mu }(q,p,1)\kappa {\textrm{e}^\kappa }\int_1^\infty {\frac{{{\textrm{e}^{ - \kappa y^{\prime}}}\,\textrm{d}y^{\prime}}}{{\sqrt {{{y^{\prime}}^2} - 1} }}} } \right)\end{equation}

by (5.14). The integral in the right-most term is identified with the respective zeroth order Bessel function ${{\rm K}_0}(\kappa )$; substituting (3.5) for w, and the combination of (5.16) and (5.17) for $\tilde{\mu }(q,p,1)$, result in

(5.52)\begin{align} {{\tilde{A}}_ - }(q,p) & = \dfrac{{\sqrt 2 }}{\rm \pi}(2{\rm \pi}{{\tilde{w}}_0}(q,p) - \tilde{\mu }(q,p,1)\kappa {\textrm{e}^\kappa }{{\rm K}_0}(\kappa ))\nonumber\\ & = 2\sqrt 2 \left( {{{\tilde{w}}_0}(q,p) - \dfrac{{{{\rm K}_0}(\kappa )}}{{{{\rm K}_0}(\kappa ) + {{\rm K}_1}(\kappa )}}{{\tilde{w}}_{3/4}}(q,p)} \right)\end{align}

by (5.23), from which

(5.53)\begin{equation}{\tilde{A}_ - }(q,p) = 2\sqrt 2 ( - (1/2){\tilde{w}_1}(q,p) + {\tilde{\varPsi }_0}(\kappa ){\tilde{w}_{3/4}}(q,p))\end{equation}

by (5.39) and (5.23).

The pair of the respective inverse transforms applied to (5.53) furnishes

(5.54)\begin{equation}{A_ - }(t,x) ={-} \sqrt 2 ({w_1}(t,x) - 2{W_{3/4}}(t,x,\tan \lambda ))\end{equation}

by (5.48), from which the leading-edge suction

(5.55)\begin{equation}{f_ - }(t,x) = ({\rm \pi}/2){({w_1}(t,x) - 2{W_{3/4}}(t,x,\tan \lambda ))^2}\end{equation}

follows by (4.15).

5.5. Sectional force, moment and power

Introducing (5.55), (5.44) and (5.45) in (3.19)–(3.25) yields

(5.56)\begin{align}{f_x}(t,x) & ={-} {\rm \pi}\dfrac{\textrm{D}}{{\textrm{D}t}}\left( {{w_0}(t,x)\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} + \theta (t,x)\tan \lambda } \right) + \dfrac{1}{8}{w_1}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial x}}} \right)\nonumber\\ & \quad - \dfrac{\rm \pi}{2}\dfrac{\partial }{{\partial x}}\left( {w_0^2(t,x) + \dfrac{1}{8}w_1^2(t,x)} \right) + \underline {{\rm \pi}\tan \lambda {w_{3/4}}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial t}}}\nonumber\\ &\quad - 2{\rm \pi}\tan \lambda W_{3/4}^2(t,x,\tan \lambda ) - 2{\rm \pi}\tan \lambda {W_{3/4}}(t,x,\tan \lambda )\nonumber\\ &\quad \times \left(\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} + \theta (t,x)\tan \lambda - \dfrac{1}{2}\dfrac{{\partial \theta (t,x)}}{{\partial x}} - {w_1}(t,x)\right),\end{align}

(5.57)\begin{align}{f_{y^{\prime}}}(t,x) & ={-} {\rm \pi}\dfrac{\textrm{D}}{{\textrm{D}t}}(\theta (t,x){w_0}(t,x)) - \underline {{\rm \pi}{w_{3/4}}(t,x){w_1}(t,x)} \nonumber\\ & \quad + 2{\rm \pi}{W_{3/4}}(t,x,\tan \lambda )({w_1}(t,x) - \theta (t,x)\tan \lambda ) - 2{\rm \pi} W_{3/4}^2(t,x,\tan \lambda ), \end{align}

(5.58)\begin{align}{f_{z^{\prime}}}(t,x) &= {\rm \pi}\frac{{\textrm{D}{w_0}(t,x)}}{{\textrm{D}t}} + 2{\rm \pi}\tan \lambda {W_{3/4}}(t,x,\tan \lambda ),\end{align}

(5.59)\begin{align} \iota (t,x) & ={-} {\rm \pi}\dfrac{\textrm{D}}{{\textrm{D}t}}\left( {{w_0}(t,x)\dfrac{{\partial {z_0}(t,x)}}{{\partial t}} + \dfrac{1}{8}{w_1}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial t}}} \right)\nonumber\\ & \quad - \dfrac{\rm \pi}{2}\dfrac{\partial }{{\partial t}}\left( {w_0^2(t,x) + \dfrac{1}{8}w_1^2(t,x)} \right) - \underline {{\rm \pi}\tan \lambda {w_{3/4}}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial t}}} \nonumber\\ & \quad - 2{\rm \pi}\tan \lambda \left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}} - \dfrac{1}{2}\dfrac{{\partial \theta (t,x)}}{{\partial t}}} \right){W_{3/4}}(t,x,\tan \lambda ), \end{align}

(5.60)\begin{align}{m_{0,x}}(t,x) &= \frac{\rm \pi}{8}\frac{{\textrm{D}{w_1}(t,x)}}{{\textrm{D}t}} + \frac{\rm \pi}{2}\tan \lambda (\underline {{w_1}(t,x)} - 2{W_{3/4}}(t,x,\tan \lambda ))\end{align}

by (4.6). As on the forward segment, the remaining two components of ${\boldsymbol{m}_0}$, ${m_{0,y^{\prime}}}$ and ${m_{0,z^{\prime}}}$, are rendered insignificant in § 6, and hence are not shown.

Broadly speaking, terms appearing first on the right-hand side of (5.56)–(5.60) embody the same terms as those appearing in (4.20)–(4.24), and they can be associated with fluid inertia. Terms involving ${W_{3/4}}$ are associated with circulatory loads – this conjecture follows by (5.31) and (5.48) because cancelling ${w_{3/4}}$ cancels both ${W_{3/4}}$ and the potential jump $\mu (t,x,1) = {\mu _0}(t,x)$ at the trailing edge; they manifest the dependence of the aerodynamic loads on the history of the body's motion. The remaining (underlined) terms are associated with inertial coupling between translational and rotational motions.

Noteworthy is the sectional moment about the quarter-chord point,

(5.61)\begin{equation}{m_{1/4,x}}(t,x) = {m_{0,x}}(t,x) + (1/2){f_z}(t,x).\end{equation}

Its explicit form

(5.62)\begin{equation}{m_{1/4,x}}(t,x) = \frac{\rm \pi}{8}\frac{{\textrm{D}{w_1}(t,x)}}{{\textrm{D}t}} + \frac{\rm \pi}{2}\tan \lambda {w_1}(t,x) + \frac{\rm \pi}{2}\frac{{\textrm{D}{w_0}(t,x)}}{{\textrm{D}t}},\end{equation}

which follows by (5.58) and (5.60), does not involve ${W_{3/4}}$, and hence is independent of the history of the body's motion. This result accords with the same result for the theory of wing sections in non-uniform motion (Sears 1940; Bisplinghoff et al. 1996; Iosilevskii 2007), where all circulatory loads on a wing section are shown to act at its quarter chord. More details can be found in § 7.1 below.

6. The entire body

6.1. Integral force, moment and power

The force acting on the entire body,

(6.1)\begin{equation}\boldsymbol{F}(t) = \int_{{x_n}}^{{x_t}} {\boldsymbol{f}(t,x)\,\textrm{d}\kern0.06em x} ,\end{equation}

follows the sectional force on the forward (4.20)–(4.22) and aft (5.56)–(5.58) segments by integration. Its components are

(6.2)\begin{align} {F_x}(t) & ={-} {\rm \pi}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {\left( {{s^2}(x){w_0}(t,x)\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} - \theta (t,x)\dfrac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}} \right) + \dfrac{{{s^4}(x)}}{8}{w_1}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial x}}} \right)\,\textrm{d}\kern0.06em x} \nonumber\\ & \quad - {\rm \pi}{\left( {{w_0}(t,x)\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} + \theta (t,x)\tan \lambda + \dfrac{{{w_0}(t,x)}}{2}} \right) + \dfrac{{{w_1}(t,x)}}{8}\left( {\dfrac{{\partial \theta (t,x)}}{{\partial x}} + \dfrac{{{w_1}(t,x)}}{2}} \right)} \right)_{x = {x_t}}}\nonumber\\ & \quad - 2{\rm \pi}\tan \lambda \int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )} \left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}} + \theta (t,x)\tan \lambda - \dfrac{1}{2}\dfrac{{\partial \theta (t,x)}}{{\partial x}} - {w_1}(t,x)} \right)\,\textrm{d}\kern0.06em x\nonumber\\ & \quad + {\rm \pi}\tan \lambda \left( {\int_0^{{x_t}} {{w_{3/4}}(t,x)} \dfrac{{\partial \theta (t,x)}}{{\partial t}}\,\textrm{d}\kern0.06em x - 2\int_0^{{x_t}} {W_{3/4}^2(t,x,\tan \lambda )\,\textrm{d}\kern0.06em x} } \right), \end{align}

(6.3)\begin{align} {F_{y^{\prime}}}(t) & ={-} {\rm \pi}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x){w_0}(t,x)\theta (t,x)\,\textrm{d}\kern0.06em x} - {\rm \pi}\theta (t,{x_t}){w_0}(t,{x_t}) - {\rm \pi}\int_0^{{x_t}} {{w_{3/4}}(t,x){w_1}(t,x)\,\textrm{d}\kern0.06em x} \nonumber\\ & \quad + 2{\rm \pi}\int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )({w_1}(t,x) - \theta (t,x)\tan \lambda )\,\textrm{d}\kern0.06em x} - 2{\rm \pi}\int_0^{{x_t}} {W_{3/4}^2(t,x,\tan \lambda )\,\textrm{d}\kern0.06em x} , \end{align}

(6.4)\begin{align}{F_{z^{\prime}}}(t) = {\rm \pi}\frac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x){w_0}(t,x)\,\textrm{d}\kern0.06em x} + {\rm \pi}{w_0}(t,{x_t}) + 2{\rm \pi}\tan \lambda \int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )\,\textrm{d}\kern0.06em x} .\end{align}

Likewise, the power needed to sustain the motion,

(6.5)\begin{equation}P(t) = \int_{{x_n}}^{{x_t}} {\iota (t,x)\,\textrm{d}\kern0.06em x} ,\end{equation}

follows the sectional power on the forward (4.23) and aft segments (5.59) with

(6.6)\begin{align} P(t) & ={-} {\rm \pi}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x){w_0}(t,x)} \left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}} + \dfrac{1}{2}{w_0}(t,x)} \right)\,\textrm{d}\kern0.06em x\nonumber\\ & \quad - \dfrac{\rm \pi}{8}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^4}(x){w_1}(t,x)} \left( {\dfrac{{\partial \theta (t,x)}}{{\partial t}} + \dfrac{1}{2}{w_1}(t,x)} \right)\,\textrm{d}\kern0.06em x\nonumber\\ & \quad - {\rm \pi}\left( {{w_0}(t,{x_t})\dfrac{{\partial {z_0}(t,{x_t})}}{{\partial t}} +\! \dfrac{1}{8}{w_1}(t,{x_t})\dfrac{{\partial \theta (t,{x_t})}}{{\partial t}}} \right) \!-\! {\rm \pi}\tan \lambda \int_0^{{x_t}} {{w_{3/4}}(t,x)\dfrac{{\partial \theta (t,x)}}{{\partial t}}\,\textrm{d}\kern0.06em x} \nonumber\\ & \quad - 2{\rm \pi}\tan \lambda \int_0^{{x_t}} {\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}} - \dfrac{1}{2}\dfrac{{\partial \theta (t,x)}}{{\partial t}}} \right){W_{3/4}}(t,x,\tan \lambda )\,\textrm{d}\kern0.06em x} . \end{align}

Given the sectional moment (per unit length) about the centre of a section, ${\boldsymbol{m}_0}(t,x)$, the moment acting on the body about the origin of $C^{\prime}$ is

(6.7)\begin{equation}\boldsymbol{M}(t) = \int_{{x_n}}^{{x_t}} {{\boldsymbol{m}_0}(t,x)\,\textrm{d}\kern0.06em x} + \int_{{x_n}}^{{x_t}} {{\boldsymbol{r}_0}(t,x) \times \boldsymbol{f}(t,x)\,\textrm{d}\kern0.06em x} ,\end{equation}

where

(6.8)\begin{equation}{\boldsymbol{r}_0}(t,x) = x{\boldsymbol{e}_x} + {y_0}(x){\boldsymbol{e}_{y^{\prime}}} + {z_0}(t,x){\boldsymbol{e}_{z^{\prime}}}\end{equation}

is the radius vector from the origin of $C^{\prime}$ to the centre of the respective cross-section. Straightforward collection of terms here leads to excessively long expressions, which render the result practically useless. The dominant contributions here (established based on the dominant arm) are $\int_{{x_n}}^{{x_t}} {x{\boldsymbol{e}_x} \times \boldsymbol{f}(t,x)\,\textrm{d}\kern0.06em x} $ in the y- and z- components, and $\int_{{x_n}}^{{x_t}} {{m_{0,x}}(t,x)\,\textrm{d}\kern0.06em x} + \int_{{x_n}}^{{x_t}} {{y_0}(x){f_{z^{\prime}}}(t,x)\,\textrm{d}\kern0.06em x} $ in the x-component; $\boldsymbol{f}$ is found in (4.20)–(4.22) and (5.56)–(5.58); ${m_{0,x}}$is found in (4.24) and (5.60). Thus, approximately,

(6.9)\begin{align} {M_x}(t) & = {\rm \pi}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {\left( {{y_0}(x){s^2}(x){w_0}(t,x) + \dfrac{1}{8}{s^4}(x){w_1}(t,x)} \right)\,\textrm{d}\kern0.06em x}\nonumber\\ & \quad + \dfrac{\rm \pi}{8}{w_1}(t,{x_t}) \!-\! {\rm \pi}{w_0}(t,{x_t}){x_t}\tan \lambda \!+\! {\rm \pi}\tan \lambda \int_0^{{x_t}} {({w_{3/4}}(t,x) \!-\! {W_{3/4}}(t,x,\tan \lambda ))\,\textrm{d}\kern0.06em x}\nonumber\\ & \quad - 2{\rm \pi}{\tan ^2}\lambda \int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )x\,\textrm{d}\kern0.06em x} + \ldots,\end{align}

(6.10)\begin{align} {M_{y^{\prime}}}(t) & ={-} {\rm \pi}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x){w_0}(t,x)x\,\textrm{d}\kern0.06em x} - 2{\rm \pi}\tan \lambda \int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )x\,\textrm{d}\kern0.06em x - {\rm \pi}{x_t}{w_0}(t,{x_t})}\nonumber\\ & \quad + {\rm \pi}\int_{{x_n}}^{{x_t}} {{s^2}(x){w_0}(t,x)\,\textrm{d}\kern0.06em x} + \ldots,\end{align}

(6.11)\begin{align} {M_{z^{\prime}}}(t) & ={-} {\rm \pi}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x){w_0}(t,x)\theta (t,x)x\,\textrm{d}\kern0.06em x} - {\rm \pi}\int_0^{{x_t}} {{w_{3/4}}(t,x){w_1}(t,x)x\,\textrm{d}\kern0.06em x}\nonumber\\ & \quad - {\rm \pi}{w_0}(t,{x_t})\theta (t,{x_t}){x_t} + {\rm \pi}\int_{{x_n}}^{{x_t}} {{s^2}(x){w_0}(t,x)\theta (t,x)\,\textrm{d}\kern0.06em x}\nonumber\\ &\quad - 2{\rm \pi}\int_0^{{x_t}} {W_{3/4}^2(t,x,\tan \lambda )x\,\textrm{d}\kern0.06em x}\nonumber\\ & \quad + 2{\rm \pi}\int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )({w_1}(t,x) - \theta (t,x)\tan \lambda )x\,\textrm{d}\kern0.06em x} + \ldots\!;\end{align}

the ellipses stand for terms of the order of $x_t^{ - 1}$ as compared with the leading ones.

6.2. Corroboration

Equations (4.20)–(4.22) and (5.56)–(5.58) for the sectional forces, (4.23) and (5.59) for the sectional power and (6.2)–(6.4), (6.6) and (6.9)–(6.11) for their integrals along the body, comprise the main practical result of this study. A few examples in the next section elucidate how they can be effectively used. Some of these examples are also used to test the coherence of these results by comparison with numerical simulations based on the vortex lattice method.

Vortex lattice method is a widely accepted numerical technique for solving the flow field in the irrotational exterior of a body and its wake (Katz & Plotkin 1991). In its simplest form, it is based on the same fundamental assumptions as the present theory – isolation of the rotational regions of the flow field (infinitesimally thin boundary layer and wake), and placement of the wake as a continuation of the boundary layer across the trailing edge – but it is free from the specific assumptions that made the present theory analytically tractable. These specific assumptions were the smallness of the slenderness parameter (the ratio between lateral and longitudinal length scales of the problem), smallness of the spatial derivatives of ${z_0}$, θ and s, and the shape of the wake footprint in a transverse plane. An agreement between numerical simulations based on this method and the theory in a variety of cases complying with the specific assumptions of the theory can be seen an indication that no significant errors were made in the algebraic derivations. A disagreement between the two in the cases that do not comply with the specific assumptions can broadly outline the applicability limits of the slender body theory within the potential flow approximation. Most of the examples of § 7 were chosen in the first category; examples of § 8 were chosen in the second one. Of course, the true test of the theory should scrutinize all its assumptions, including those of the potential flow approximation (the thinness of the rotational regions of the flow and their location), which can be done experimentally or by numerical simulations of viscous fluid flow – see § 8.

6.3. Notations

As the examples of § 7 are divided between aerodynamics of slender bodies and the hydrodynamics of aquatic propulsion, it is worthwhile to relate the present notation with commonly accepted ones in each of these areas. Referring to the end of § 2.1, the reader is reminded that the units of pressure, length and area are $\rho {v^2}$, ${s_0} = s(0)$ and $s_0^2$, respectively. In aerodynamics, the commonly accepted unit of pressure is $(1/2)\rho {v^2}$, and the unit of area is (typically) the area of the body projection onto the x–y plane, ${S_w}$; the unit of length is hardly uniform and depends on the particular circumstances. Having the shape of the forward segment left undefined, the projected body area remains undefined as well, but the notion of the aspect ratio

(6.12)\begin{equation}A = {(2 + {x_t}\tan \lambda )^2}/{S_w},\end{equation}

which is the ratio of the square of the body span $2 + {x_t}\tan \lambda $ and the area of its projection onto the x–y plane, can be effectively used to replace the area. Thus, keeping the unit of length as ${s_0}$, the aerodynamic coefficients of lift ${C_L} = {C_{{F_{z^{\prime}}}}}$, drag ${C_D} = {C_{{F_{x^{\prime}}}}}$and side force ${C_Y} = {C_{{F_{y^{\prime}}}}}$, as well as those of roll ${C_R} ={-} {C_{{M_{x^{\prime}}}}}$, pitch ${C_M} = {C_{{M_{x^{\prime}}}}}$and yaw ${C_N} = {C_{{M_{z^{\prime}}}}}$ moments, follow the present results with

(6.13)\begin{equation}{C_{\ldots} } = \frac{2}{{{S_w}}}( \ldots ) = \frac{{2A}}{{{{(2 + {x_t}\tan \lambda )}^2}}}( \ldots ),\end{equation}

where the ellipsis is a placeholder for ${F_{x^{\prime}}},{F_{y^{\prime}}},{F_{z^{\prime}}}$ and ${M_{x^{\prime}}},{M_{y^{\prime}}},{M_{z^{\prime}}}$.

There is no commonly adopted choice of units in hydrodynamics of aquatic propulsion, and hence no different normalization is needed. Nonetheless, the common names do change. Thus, ${F_{y^{\prime}}}$ becomes the dorso-ventral component of the hydrodynamic force and, to within a sign, it becomes associated with ‘lift’ (practically no biological swimmer is neutrally buoyant, and hence relies on hydrodynamic lift to counteract gravity); ${F_{z^{\prime}}}$ becomes the ‘side force’ and $- {F_{x^{\prime}}}$ becomes the ‘thrust’.

7. Examples

7.1. A rigid wing

As a first example, consider the sectional lift ${f_{z^{\prime}}}$ and rolling (twisting) moment ${m_{{1 / 4},x}}$ acting on the aft segment of a (rigid, non-flexible) wing that moves in such a way that ${z_0}$ and $\theta $ do not change along it, but do change with time. One can envision this motion as a combination of heave and rotation about the long axis of the wing. A change of variables, $\bar{t} = t\tan \lambda $ and $\bar{x} = x\tan \lambda $, will prove helpful here. Consistently marking functions of $\bar{t}$ and $\bar{x}$ by overbars, as in ${z_0}(t) = {z_0}(\bar{t}\cot \lambda ) = {\bar{z}_0}(\bar{t})$ and $\theta (t) = \theta (\bar{t}\cot \lambda ) = \bar{\theta }(\bar{t})$, one will find ${w_0}$ related to ${\bar{w}_0}$ by

(7.1)\begin{equation}{w_0}(t) = \tan \lambda {\bar{w}_0}(\bar{t}),\end{equation}

where

(7.2)\begin{equation}{\bar{w}_0}(\bar{t}) ={-} \frac{{\textrm{d}{{\bar{z}}_0}(\bar{t})}}{{\textrm{d}\bar{t}}} - \bar{\theta }(\bar{t})\end{equation}

by (3.6). One will also find ${w_1}$ and ${w_{3/4}}$ related to ${\bar{w}_1}$ and ${\bar{w}_{3/4}}$ by variants of (7.1), where ${\bar{w}_1}$ and ${\bar{w}_{3/4}}$are replicas of (3.7) and (5.24) with overbars. Subsequently, (5.58) and (5.62) become

(7.3)\begin{gather}{f_{z^{\prime}}}(t,x) = {\tan ^2}\lambda\, {\bar{f}_{z^{\prime}}}(t\tan \lambda ,x\tan \lambda ),\end{gather}

(7.4)\begin{gather}{m_{1/4,x}}(t,x) = {\tan ^2}\lambda\, {\bar{m}_{1/4,x}}(t\tan \lambda ),\end{gather}

where

(7.5)\begin{gather}\hspace{-14pc}{{\bar{f}}_{z^{\prime}}}(\bar{t},\bar{x}) ={-} {\rm \pi}\left( {\dfrac{{{\textrm{d}^2}{{\bar{z}}_0}(\bar{t})}}{{\textrm{d}{{\bar{t}}^2}}} + \dfrac{{\textrm{d}\bar{\theta }(\bar{t})}}{{\textrm{d}\bar{t}}}} \right)\nonumber\\ \hspace{5pc} +\, 2{\rm \pi}\left( {{\varPsi_1}({{\bar{x}}_{\ast} }){{\bar{w}}_{{3 / 4}}}(\bar{t} - {{\bar{x}}_{\ast} }) + \int_0^{{{\bar{x}}_{\ast} }} {{\varPsi_1}(\bar{x}^{\prime})\dfrac{{\textrm{d}{{\bar{w}}_{3/4}}(\bar{t} - \bar{x}^{\prime})}}{{\textrm{d}\bar{t}}}\,\textrm{d}\bar{x}^{\prime}} } \right),\end{gather}

(7.6)\begin{gather}{\bar{m}_{1/4,x}}(\bar{t}) ={-} \frac{\rm \pi}{2}\left( {\frac{{{\textrm{d}^2}{{\bar{z}}_0}(\bar{t})}}{{\textrm{d}{{\bar{t}}^2}}} + \frac{1}{4}\frac{{{\textrm{d}^2}\bar{\theta }(\bar{t})}}{{\textrm{d}{{\bar{t}}^2}}} + 2\frac{{\textrm{d}\bar{\theta }(\bar{t})}}{{\textrm{d}\bar{t}}}} \right)\end{gather}

by (5.46). Recall that ${\bar{x}_{\ast} } = \min (\bar{t},\bar{x})$ by (5.30). An alternative form of (7.5),

(7.7)\begin{equation}{\bar{f}_{z^{\prime}}}(\bar{t},\bar{x}) ={-} {\rm \pi}\left( {\frac{{{\textrm{d}^2}{{\bar{z}}_0}(\bar{t})}}{{\textrm{d}{{\bar{t}}^2}}} + \frac{{\textrm{d}\bar{\theta }(\bar{t})}}{{\textrm{d}\bar{t}}}} \right) + 2{\rm \pi}\int_0^{{{\bar{x}}_{\ast} }} {{\varPsi _0}(\bar{x}^{\prime}){{\bar{w}}_{{3 / 4}}}(\bar{t} - \bar{x}^{\prime})\,\textrm{d}\bar{x}^{\prime}} ,\end{equation}

follows by (5.43) and (5.42) after integration by parts, but it could have been derived directly using (5.48) instead of (5.46).

Here, ${\bar{f}_{z^{\prime}}}$ and ${\bar{m}_{1/4,x}}$ can be interpreted as reduced loads that are based on $v\tan \lambda $ as the unit of speed instead of v. Because $\lambda \ll 1$ by assumption, $\tan \lambda $ and $\sin \lambda $ are essentially the same, and therefore $v\tan \lambda $ is practically the velocity component normal to the leading edge of the aft segment. With this interpretation, (7.5) and (7.6) can be compared with the corresponding equations from the theory of wing sections in unsteady motion – for example, equations (5-370) and (5-312) of Bisplinghoff et al. (1996). Adjusting notation with $b \to {s_0}$, $\alpha \to \theta $, $h \to {s_0}({z_0} + a\theta )$, $a ={-} 1/2$, $U \to v\tan \lambda $ and $\textrm{an}\;\textrm{overdot} \to (v\tan \lambda /{s_0})\,\textrm{d}/\textrm{d}\bar{t}$, equation (5-370) yields ${\bar{f}_{z^{\prime}}}(\bar{t},\bar{t})$ instead of ${\bar{f}_{z^{\prime}}}(\bar{t},{\bar{x}_{\ast} })$ in (7.5), whereas equation (5-312) recovers (7.6) exactly. The difference between ${\bar{f}_{z^{\prime}}}(\bar{t},\bar{t})$ and ${\bar{f}_{z^{\prime}}}(\bar{t},{\bar{x}_{\ast} })$ is the extent of the wake: it is $\bar{t} = t\tan \lambda $ with a section of an infinite wing, and ${\bar{x}_{\ast} } = \tan \lambda \min (t,x)$ with the (particular) section of a slender wing, situated at distance x from the forward end of the aft segment. The two are equal when $\bar{t} \le \bar{x}$, but once $\bar{t}$ exceeds $\bar{x}$, the variable extent of the wake to the side of a slender wing introduces non-uniformity in the aerodynamic loads acting on its aft segment. In a sense, it resembles the impulsive start analogy of Cheng (1954) for a delta wing. The equivalence between (5-312) and (7.6) is consistent with the idea that circulatory loads (the term with the integral in (7.5)), although dependent on the extent of the wake, act at the quarter-chord point.

When the wing oscillates harmonically with no twist, i.e. when ${\bar{z}_0}(\bar{t}) = Re({\hat{z}_0}\,{\textrm{e}^{\textrm{i}\bar{\omega }\bar{t}}})$ and $\bar{\theta }(\bar{t}) = 0$, and it does so for sufficiently long time $(\bar{t} \ge \bar{x})$, (7.7) reduces to ${\bar{f}_{z^{\prime}}}(\bar{t},\bar{x}) = Re({\hat{f}_{z^{\prime}}}\textrm{(}\bar{x}\textrm{)}\,{\textrm{e}^{\textrm{i}\bar{\omega }\bar{t}}})$, where

(7.8)\begin{equation}{\hat{f}_{z^{\prime}}}(\bar{x}) = {\rm \pi}{\hat{z}_0}\left( {{{\bar{\omega }}^2} + 2\textrm{i}\bar{\omega }\int_0^{\bar{x}} {{\varPsi_0}\textrm{(}\bar{x}^{\prime}\textrm{)}\,{\textrm{e}^{ - \textrm{i}\bar{\omega }\bar{x}^{\prime}}}\,\textrm{d}\bar{x}^{\prime}} } \right).\end{equation}

Because ${\varPsi _0}$ is strictly positive on $(0,\infty )$ (Appendix F), the absolute value of its integral in (7.8) can be bounded by its zero-frequency limit, which is ${\varPsi _1}(\bar{x})$ by (5.43). It is an order-1 quantity (Appendix F). Consequently, when $\bar{\omega } \gg 1$, the sectional force is dominated by its inertial constituent ${\rm \pi}{\hat{z}_0}{\bar{\omega }^2}$, which is unaffected by the presence of the wake. Noting that $\bar{\omega } = \omega \cot \lambda $ (in fact, $\bar{\omega }\bar{t} = \omega t$), the case $\bar{\omega } \gg 1$ can be a very real possibility, even at low frequencies. In fact, when $\lambda = 0$, only inertial forces act on the aft segment.

7.2. Impulsive start

As a second example, consider integral forces acting on a wing that is impulsively thrown into a fixed bent ${z_0}(t,x) = {\rm H}(t){\hat{z}_0}(x)$ and a uniform cant-in angle $\theta (t,x) = {\rm H}(t){\hat{\theta }_0}$. In this case,

(7.9)\begin{gather}{w_0}(t,x) ={-} \delta (t){\hat{z}_0}(x) + {\rm H}(t){\hat{w}_0}(x),\end{gather}

(7.10)\begin{gather}{\hat{w}_0}(x) ={-} \frac{{\textrm{d}{{\hat{z}}_0}(x)}}{{\textrm{d}\kern0.06em x}} + {\hat{\theta }_0}\frac{{\textrm{d}{y_0}(x)}}{{\textrm{d}\kern0.06em x}}\end{gather}

by (3.6);

(7.11)\begin{equation}{w_1}(t,x) ={-} \delta (t){\hat{\theta }_0}\end{equation}

by (3.7); ${w_{3/4}}$ follows ${w_0}$ and ${w_1}$ by (5.24). The three components of the force and the pitching moment acting on the wing after its shape has been set (i.e. at $t > 0$),

(7.12)\begin{gather}{F_x}(t) = \frac{\rm \pi}{2}\hat{w}_0^2({x_t}) + 2{\rm \pi}\tan \lambda \left( {\int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda ){{\hat{w}}_0}(x)\,\textrm{d}\kern0.06em x} - \int_0^{{x_t}} {W_{3/4}^2(t,x,\tan \lambda )\,\textrm{d}\kern0.06em x} } \right),\end{gather}

(7.13)\begin{gather}{F_{y^{\prime}}}(t) ={-} {\hat{\theta }_0}{F_{z^{\prime}}}(t) - 2{\rm \pi}\int_0^{{x_t}} {W_{3/4}^2(t,x,\tan \lambda )\,\textrm{d}\kern0.06em x} ,\end{gather}

(7.14)\begin{gather}{F_{z^{\prime}}}(t) = {\rm \pi}{\hat{w}_0}({x_t}) + 2{\rm \pi}\tan \lambda \int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )\,\textrm{d}\kern0.06em x,}\end{gather}

(7.15)\begin{align}{M_{y^{\prime}}}(t) & = {\rm \pi}\int_{{x_n}}^0 {{s^2}(x){{\hat{w}}_0}(x)\,\textrm{d}\kern0.06em x} + {\rm \pi}\int_0^{{x_t}} {({{\hat{w}}_0}(x) - {{\hat{w}}_0}({x_t}))\,\textrm{d}\kern0.06em x} \nonumber\\ & \quad - 2{\rm \pi}\tan \lambda \int_0^{{x_t}} {{W_{3/4}}(t,x,\tan \lambda )x\,\textrm{d}\kern0.06em x + \ldots ,} \end{align}

follow by (6.2)–(6.4), (6.1), (5.7) and the identity ${\hat{w}_0}({x_t}){x_t} = \int_0^{{x_t}} {{{\hat{w}}_0}({x_t})\,\textrm{d}\kern0.06em x}$. As in the classical slender body theory, the force acting on the wing is explicitly independent of the shape of the forward segment.

Being the only time-dependent quantity in (7.12)–(7.15), the wake contribution, which presently takes on the form

(7.16)\begin{align} {W_{3/4}}(t,x,\tan \lambda ) & ={-} \tan \lambda\, {\varPsi _\textrm{0}}\textrm{(}t\tan \lambda \textrm{)}\,{\rm H}(x - t)\left( {{{\hat{z}}_0}\textrm{(}x - t\textrm{) + }\dfrac{1}{2}{{\hat{\theta }}_0}} \right)\nonumber\\ & \quad + \tan \lambda \int_0^{\min (t,x)} {{\varPsi _\textrm{0}}(x^{\prime}\tan \lambda ){{\hat{w}}_0}(x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}} , \end{align}

is the one that governs the transient response of aerodynamic loads. In this particular form, it follows (5.48) by (7.9), (7.11), (5.24) and (5.30). It vanishes when $\lambda \to 0$ and no wake forms near the body. It becomes independent of time when t exceeds x,

(7.17)\begin{equation}{W_{3/4}}(t,x,\tan \lambda ) = \tan \lambda \int_0^x {{\varPsi _\textrm{0}}(x^{\prime}\tan \lambda ){{\hat{w}}_0}(x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}} ,\end{equation}

and hence all aerodynamic loads reach a steady state when t exceeds ${x_t}$.

Equations (7.12)–(7.16) become much simpler when

(7.18)\begin{equation}{\hat{w}_0}(x) = \alpha \end{equation}

does not change along the wing (α in this case can be interpreted as the angle of attack), and when it is set by rotation of the wing about the 3/4-chord line of the aft segment, so that

(7.19a,b)\begin{equation}{\hat{\theta }_0} ={-} \alpha \cot \lambda \quad \textrm{and}\quad {\hat{z}_0}(x) ={-} (1/2){\hat{\theta }_0}\end{equation}

for every point along it. Rotation about the 3/4-chord line eliminates the velocity spike when θ is set (at $t = 0$), and thus cancels the first term on the right-hand side of (7.16). In fact, with (7.18) and (7.19), (7.16) reduces to

(7.20)\begin{equation}{W_{3/4}}(t,x,\tan \lambda ) = \alpha {\varPsi _\textrm{1}}(\min (t,x)\tan \lambda )\end{equation}

by (5.43), and (7.12)–(7.15) become

(7.21)\begin{gather}{F_x}(t) = {\rm \pi}{\alpha ^2}({\textstyle{1 \over 2}} + 2{\varOmega _{10}}(t\tan \lambda ,{x_t}\tan \lambda ) - 2{\varOmega _{20}}(t\tan \lambda ,{x_t}\tan \lambda )),\end{gather}

(7.22)\begin{gather}{F_{y^{\prime}}}(t) = {\rm \pi}{\alpha ^2}\cot \lambda (1 + 2{\varOmega _{10}}(t\tan \lambda ,{x_t}\tan \lambda ) - 2{\varOmega _{20}}(t\tan \lambda ,{x_t}\tan \lambda )),\end{gather}

(7.23)\begin{gather}{F_{z^{\prime}}}(t) = {\rm \pi}\alpha (1 + 2{\varOmega _{10}}(t\tan \lambda ,{x_t}\tan \lambda )),\end{gather}

(7.24)\begin{gather}{M_{y^{\prime}}}(t) = {\rm \pi}\alpha \left( {\int_{{x_n}}^0 {{s^2}(x)\,\textrm{d}\kern0.06em x - 2\cot \lambda {\Omega_{11}}(t\tan \lambda ,{x_t}\tan \lambda ) + \ldots } } \right),\end{gather}

where

(7.25)\begin{equation}{\varOmega _{nm}}(t,x) = \int_0^x {\varPsi _1^n(\min (t,x^{\prime})){{x^{\prime}}^m}\,\textrm{d}\kern0.06em x^{\prime}} \end{equation}

are standard quadratures of ${\varPsi _1}$ (Appendix G). The terms enclosed by parentheses in (7.21)–(7.24) are shown in figure 5. The transient response indeed weakens with decreasing λ and the steady state is indeed reached at $t = {x_t}$.

Figure 5. Drag (a), side force (b) and lift (c) as functions of time after an impulsive start for a few values of $\lambda $ shown to the right of the respective lines. Pitching moment about the origin is shown in (d). Numerical simulations are represented by circles (down sampled for display); (7.21)–(7.24) are shown by solid lines. Simulation details are those of case 1 in table 1 with ${\hat{\theta }_0} ={-} 0.1$. $\alpha = {\hat{\theta }_0}\tan \lambda $.

7.3. Steady flight

When t exceeds ${x_t}$, ${\varOmega _{nm}}$ reduce to their respective limits

(7.26)\begin{equation}{\varOmega _{nm}}(x,x) = {\varOmega _{nm}}(\infty ,x) = \int_0^x {\varPsi _1^n(x^{\prime}){{x^{\prime}}^m}\,\textrm{d}\kern0.06em x^{\prime}} ,\end{equation}

and (7.21)–(7.24) become

(7.27)\begin{gather}{F_x}(\infty ) = {\rm \pi}{\alpha ^2}\left( {\frac{1}{2} + 2{\varPsi_2}({x_t}\tan \lambda ) - 2\int_0^{{x_t}\tan \lambda } {\varPsi_1^2(x)\,\textrm{d}\kern0.06em x} } \right),\end{gather}

(7.28)\begin{gather}{F_{y^{\prime}}}(\infty ) = {\rm \pi}{\alpha ^2}\cot \lambda \left( {1 + 2{\varPsi_2}({x_t}\tan \lambda ) - 2\int_0^{{x_t}\tan \lambda } {\varPsi_1^2(x)\,\textrm{d}\kern0.06em x} } \right),\end{gather}

(7.29)\begin{gather}{F_{z^{\prime}}}(\infty ) = {\rm \pi}\alpha (1 + 2{\varPsi _2}({x_t}\tan \lambda )),\end{gather}

(7.30)\begin{gather}{M_{y^{\prime}}}(\infty ) = {\rm \pi}\alpha \int_{{x_n}}^0 {{s^2}(x)\,\textrm{d}\kern0.06em x} - 2{\rm \pi}\alpha {x_t}\left( {{\varPsi_2}({x_t}\tan \lambda ) - \frac{{{\varPsi_3}({x_t}\tan \lambda )}}{{{x_t}\tan \lambda }}} \right) + \ldots ;\end{gather}

details can be found in Appendix G.

The three components of the force are shown in figure 6(a,b). Two limits of lift, ${\lim _{{x_t}\tan \lambda \to 0}}{F_{z^{\prime}}}(\infty ) = {\rm \pi}\alpha $ and ${\lim _{{x_t}\tan \lambda \to \infty }}{F_{z^{\prime}}}(\infty ) = 2{\rm \pi}\alpha {x_t}\tan \lambda$, follow (7.29) by (F5) and (F6). Using (6.13) to adjust notation, the former yields ${\lim _{{x_t}\tan \lambda \to 0}}{C_L} = {\rm \pi}\alpha A/2$, which recovers the lift coefficient of a slender wing (Jones 1946; Katz & Plotkin 1991); the latter yields ${\lim _{{x_t}\tan \lambda \to \infty }}{C_L} = 2{\rm \pi}\alpha \sin \lambda + \ldots$, which recovers the lift coefficient of a swept wing of infinite aspect ratio (Thwaites 1960). Recall that, for small λ, $\tan \lambda $ and $\sin \lambda $ are equivalent, whereas for large ${x_t}$, ${S_w} = 2{x_t} + \ldots\, $.

Figure 6. Drag (black) (a), side force (blue) (a), lift (b), induced drag fraction (c) and aerodynamic centre (d) of straight swept wing as functions of $\lambda $. Circles mark numerical simulations; lines represent (7.27)–(7.29), (7.31) and (7.34). Note the scale in (c). Simulation details are those of cases 2 (${\hat{\theta }_0} ={-} 0.02$, circles) and 3 (${\hat{\theta }_0} ={-} 0.08$, diamonds) from table 1. $\alpha = {\hat{\theta }_0}\tan \lambda $.

Location of the aerodynamic centre,

(7.31)\begin{equation}{x_{ac}} = \frac{1}{{1 + 2{\varPsi _2}({x_t}\tan \lambda )}}\Bigg( { - \int_{{x_n}}^0 {{s^2}(x)\,\textrm{d}\kern0.06em x} + 2{x_t}\left( {{\varPsi_2}({x_t}\tan \lambda ) - \frac{{{\varPsi_3}({x_t}\tan \lambda )}}{{{x_t}\tan \lambda }}} \right)} \Bigg),\end{equation}

follows (7.29) and (7.30) by its definition

(7.32)\begin{equation}{x_{ac}} ={-} \frac{{\partial {M_{y^{\prime}}}(\infty )/\partial \alpha }}{{\partial {F_{z^{\prime}}}(\infty )/\partial \alpha }}\end{equation}

as a point where the pitching moment is independent of the angle of attack. The first term on the right-hand side of (7.31) can be identified with the aerodynamic centre of the forward segment,

(7.33)\begin{equation}{x_{ac,f}} ={-} \int_{{x_n}}^0 {{s^2}(x)\,\textrm{d}\kern0.06em x}.\end{equation}

This conjecture can be accepted either as a formal limit ${x_{ac,f}} = {\lim _{{x_t} \to 0}}{x_{ac}}$ (note (F6)), or as a manifestation of the well-known result of the slender body theory (Jones 1946; Katz & Plotkin 1991). For a triangular shaped forward segment, such as the one used in the numerical simulations, ${x_{ac,f}} = {x_n}/3$. With increasing length of the aft segment, the aerodynamic centre moves from ${x_{ac,f}}$ toward the mid-length section of the aft segment (figure 6d).

The ratio ${\bar{F}_x}$ between the drag of the wing ${F_{x^{\prime}}}(\infty )$ and the drag ${F_{x,e}} = 2F_{z^{\prime}}^2(\infty )/{\rm \pi} \mathrm{(}2 + {x_t}\tan \lambda {\textrm{)}^2}$ of a hypothetical wing of the same aspect ratio that generates the same overall lift with an elliptical spanwise distribution (equivalence between this expression and $C_L^2/{\rm \pi} A$ can be verified using (6.13)), is a measure of its aerodynamic efficiency. Its explicit form,

(7.34)\begin{equation}{\bar{F}_x} = {\left( {\frac{{2 + {x_t}\tan \lambda }}{{2 + 4{\varPsi_2}({x_t}\tan \lambda )}}} \right)^2}\left( {1 + 4{\varPsi_2}({x_t}\tan \lambda ) - 4\int_0^{{x_t}\tan \lambda } {\varPsi_1^2(x)\,\textrm{d}\kern0.06em x} } \right),\end{equation}

follows by (7.27) and (7.29). It equals unity when ${x_t}\tan \lambda \to 0$ by (F5), manifesting an elliptical lift distribution over the span of a small-aspect-ratio wing. It cannot be unity for all ${x_t}\tan \lambda $, and hence one can say with confidence that ${\bar{F}_x} > 1$ (figure 6c), and that the lift distribution is not elliptical. Having only the leading-order asymptotic behaviour of the indicial functions involved (manifested in (F6) and (G3)), the limit ${x_t}\tan \lambda \to \infty $ is meaningless.

7.4. Anguilliform swimming gait

As the last example, consider an anguilliform (an eel-like) swimmer that propels itself by small-amplitude lateral deformation waves

(7.35)\begin{equation}{z_0}(t,x) = {\hat{z}_t}\zeta (x)\cos (\omega t - kx)\end{equation}

that propagate backwards along its body with phase velocity $u = \omega /k > 1$. Here, ${\hat{z}_t}$ is the tail amplitude, $\zeta $ is the (monotonic) modulating shape function $({x_n},{x_t}) \to (0,1)$ and ω and k are the (angular) frequency and wavenumber. To simplify this example, it will be assumed that the swimmer does not twist, i.e.

(7.36)\begin{equation}\theta (t,x) = 0.\end{equation}

Consistent with preceding assumptions, $\lambda $ is assumed strictly positive; notwithstanding, it is presently assumed to be sufficiently small to justify keeping only the leading-order terms with respect to $\tan \lambda $ – this is not a trivial assumption because some of these terms involve its product with ${x_t}$, which can be a large quantity. Positiveness of $\lambda $ implies that when associating this model swimmer with a yellow-bellied sea snake, which swims with its dorsal side leading (Graham et al. 1987), the lower edge on figures 1–3 should be the dorsal one.

The components of the force acting on the body are given by (6.2)–(6.4); the power needed to move it is given in (6.6). The value of ${W_{3/4}}$, that appears in each one of them, is given by (5.48). For (very) small $\lambda $, it can be approximated by

(7.37)\begin{align}{W_{3/4}}(t,x,\tan \lambda ) & = \tan \lambda \int_0^{{x_{\ast} }} {\left( {\dfrac{{\delta (x^{\prime}\tan \lambda )}}{2} + \dfrac{{{\rm H}(x^{\prime}\tan \lambda )}}{8} + \ldots } \right)} {w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}\nonumber\\ & = \dfrac{1}{2}{w_{3/4}}(t,x) + \dfrac{1}{8}\tan \lambda \int_0^{{x_{\ast} }} {{w_{3/4}}(t - x^{\prime},x - x^{\prime})\,\textrm{d}\kern0.06em x^{\prime}} + \ldots,\end{align}

where the ellipsis stands for terms of the higher order with respect to $\tan \lambda $, and the term in the parentheses on the first line of this equation is the expansion of ${\varPsi _\textrm{0}}$ near the origin (F3). It is tacitly assumed that the swimmer has been moving for some time already, so that ${x_{\ast} } = \min (t,x)$ in the upper limit can be replaced by x. Moreover, with $\theta (t,x) = 0$, ${w_{3/4}} ={-} \textrm{D}{z_0}/\textrm{D}t$ by (3.6), (3.7) and (5.24). Consequently,

(7.38)\begin{equation}{W_{3/4}}(t,x,\tan \lambda ) ={-} \frac{1}{2}\frac{{\textrm{D}{z_0}({t,x} )}}{{\textrm{D}t}} + \frac{1}{8}\tan \lambda ({z_0}(t - x,0) - {z_0}(t,x)) + \ldots \end{equation}

by (5.47), and (6.2)–(6.4) and (6.6) reduce to

(7.39)\begin{gather} {F_x}(t) = {\rm \pi}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x)\dfrac{{\textrm{D}{z_0}(t,x)}}{{\textrm{D}t}}\,\textrm{d}\kern0.06em x} - \dfrac{\rm \pi}{2}{\Bigg( {{{\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}}} \right)}^2} - {{\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}}} \right)}^2}} \Bigg)_{x = {x_t}}}\nonumber\\ \quad - \dfrac{\rm \pi}{2}\tan \lambda \int_0^{{x_t}} {\Bigg( {{{\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}}} \right)}^2} - {{\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}}} \right)}^2}} \Bigg)\,\textrm{d}\kern0.06em x} + \ldots ,\end{gather}

(7.40)\begin{gather}{F_{y^{\prime}}}(t) ={-} \frac{\rm \pi}{2}\int_0^{{x_t}} {{{\left( {\frac{{\textrm{D}{z_0}(t,x)}}{{\textrm{D}t}}} \right)}^2}\,\textrm{d}\kern0.06em x} + \ldots ,\end{gather}

(7.41)\begin{align}{F_{z^{\prime}}}(t) &={-} {\rm \pi}\frac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x)\frac{{\textrm{D}{z_0}(t,x)}}{{\textrm{D}t}}\,\textrm{d}\kern0.06em x} - {\rm \pi}\frac{{\textrm{D}{z_0}(t,{x_t})}}{{\textrm{D}t}} - {\rm \pi}\tan \lambda \int_0^{{x_t}} {\frac{{\textrm{D}{z_0}(t,x)}}{{\textrm{D}t}}\,\textrm{d}\kern0.06em x} + \ldots ,\end{align}

(7.42)\begin{align} P(t) & = \dfrac{\rm \pi}{2}\dfrac{\partial }{{\partial t}}\int_{{x_n}}^{{x_t}} {{s^2}(x)\Bigg( {{{\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}}} \right)}^2} \!-\! {{\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial x}}} \right)}^2}} \Bigg)\,\textrm{d}\kern0.06em x} \!+\! {\rm \pi}{\left( {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}}\dfrac{{\textrm{D}{z_0}(t,x)}}{{\textrm{D}t}}} \right)_{x = {x_t}}}\nonumber\\ & \quad + {\rm \pi}\tan \lambda \int_0^{{x_t}} {\dfrac{{\partial {z_0}(t,x)}}{{\partial t}}\dfrac{{\textrm{D}{z_0}(t,x)}}{{\textrm{D}t}}\,\textrm{d}\kern0.06em x} + \ldots,\end{align}

where the ellipses stand for the higher-order terms with respect to $\tan \lambda $. No term explicitly involving $\tan \lambda $ was included in (7.40), because the term retained is already the leading-order term with respect to $\lambda $ – it would have vanished identically if $\lambda $ were zero. Its existence is a direct consequence of the assumption that $\lambda $ is strictly positive (§ 2.1), that made the long edges of the aft segment dissimilar, with suction acting only on the lower (leading) edge (§ 5.4). With no sweep and no twist, there would have been no difference between the edges, and ${F_{y^{\prime}}}$ would have vanished. The zeroth-order terms with respect to $\tan \lambda $ in the remaining equations can be identified with the respective results of Part 1. Coherence of (7.39)–(7.42) is verified in figure 7.

Figure 7. Time histories of thrust $- {F_x}$, power P, lift ${F_{y^{\prime}}}$ and side force ${F_{z^{\prime}}}$ during a single tail beat for a few values of $\lambda $ indicated to the right of the respective lines. Points mark numerical simulations, (6.2)–(6.4) and (6.6) are represented by solid lines; (7.39)–(7.42) are dashed. The set with $\lambda = 0.1$ is not shown in (c) to avoid clutter; the dashed line in this panel is the same for both data sets shown. Schematic top views of the swimmer during the tail beat are shown between the two lines; they correspond to the times where its head lays. Simulation details are those of case 4 in table 1.

Swimming performance is commonly characterized by period-averaged quantities. Under a tacit assumption that ${z_0}$ is periodic with zero mean, time averages of (7.39)–(7.42) furnish

(7.43)\begin{gather}\langle {F_x}\rangle ={-} \frac{\rm \pi}{2}{\Bigg\langle {{{\left( {\frac{{\partial {z_0}}}{{\partial t}}} \right)}^2} - {{\left( {\frac{{\partial {z_0}}}{{\partial x}}} \right)}^2}} \Bigg\rangle _{x = {x_t}}} - \frac{\rm \pi}{2}\tan \lambda \int_0^{{x_t}} {\Bigg\langle {{{\left( {\frac{{\partial {z_0}}}{{\partial t}}} \right)}^2} - {{\left( {\frac{{\partial {z_0}}}{{\partial x}}} \right)}^2}} \Bigg\rangle \,\textrm{d}\kern0.06em x} + \ldots ,\end{gather}

(7.44)\begin{gather}\langle {F_{y^{\prime}}}\rangle ={-} \frac{\rm \pi}{2}\int_0^{{x_t}} {\Bigg\langle {{{\left( {\frac{{D{z_0}}}{{Dt}}} \right)}^2}} \Bigg\rangle \,\textrm{d}\kern0.06em x} + \ldots ,\end{gather}

(7.45)\begin{gather}\langle P\rangle = {\rm \pi}{\left\langle {\frac{{\textrm{D}{z_0}}}{{\textrm{D}t}}\frac{{\partial {z_0}}}{{\partial t}}} \right\rangle _{x = {x_t}}} + {\rm \pi}\tan \lambda \int_0^{{x_t}} {\left\langle {\frac{{\textrm{D}{z_0}}}{{\textrm{D}t}}\frac{{\partial {z_0}}}{{\partial t}}} \right\rangle \,\textrm{d}\kern0.06em x} + \ldots ,\end{gather}

and, of course, $\langle {F_{z^{\prime}}}\rangle = 0$. The zeroth-order terms in (7.43) and (7.45) are those found in (3.26) and (3.29) of Part 1 for the swimmer that ends at ${x_t} = 0$. The zeroth-order term in (7.44) is zero. Explicit forms of (7.43)–(7.45) under (7.35) are

(7.46)\begin{gather}\langle {F_x}\rangle ={-} \frac{\rm \pi}{4}\hat{z}_t^2\left( {{\omega^2} - {k^2} - {{\dot{\zeta }}^2}({x_t}) + \tan \lambda \int_0^{{x_t}} {(({\omega^2} - {k^2}){\zeta^2}(x) - {{\dot{\zeta }}^2}(x))\,\textrm{d}\kern0.06em x} + \ldots } \right),\end{gather}

(7.47)\begin{gather}\langle {F_{y^{\prime}}}\rangle ={-} \frac{\rm \pi}{4}\hat{z}_t^2\int_0^{{x_t}} {({{(\omega - k)}^2}{\zeta ^2}(x) + {{\dot{\zeta }}^2}(x))} \,\textrm{d}\kern0.06em x + \ldots ,\end{gather}

(7.48)\begin{gather}\langle P\rangle = \frac{\rm \pi}{2}\hat{z}_t^2\omega (\omega - k)\left( {1 + \tan \lambda \int_0^{{x_t}} {{\zeta^2}(x)\,\textrm{d}\kern0.06em x} + \ldots } \right),\end{gather}

where an overdot marks a derivative. Recall that $\zeta ({x_t}) = 1$ by assumption (see the paragraph following (7.35)).

Propulsion efficiency can be defined as a ratio

(7.49)\begin{equation}\eta ={-} \langle {F_x}\rangle /\langle P\rangle \end{equation}

of the period-averaged power made good $\langle {F_x}\rangle$ (recall that the swimming velocity is used as a unit of speed) and the power actually spent $\langle P\rangle $. It follows by (7.43) and (7.45) in general, and by (7.46) and (7.48) in particular. The last pair yields

(7.50)\begin{equation}\eta = \frac{{{\omega ^2} - {k^2} - {{\dot{\zeta }}^2}({x_t})}}{{2\omega (\omega - k)}}\Bigg( {1 + \tan \lambda \int_0^{{x_t}} {\frac{{{\zeta^2}(x){{\dot{\zeta }}^2}({x_t}) - {{\dot{\zeta }}^2}(x)}}{{{\omega^2} - {k^2} - {{\dot{\zeta }}^2}({x_t})}}\,\textrm{d}\kern0.06em x} + \ldots } \Bigg).\end{equation}

Exponential modulating amplitude,

(7.51)\begin{equation}\zeta (x) = {\textrm{e}^{\beta (x - {x_t})}},\end{equation}

makes the integral on the right-hand side of (7.50) vanish, rendering the effect of $\lambda $ on propulsion efficiency negligible. Modulating amplitude with $\dot{\zeta }({x_t}) = 0$ renders this effect detrimental (as long as positive thrust is being generated). Thus said, an ‘exact’ solution, based on (6.2)–(6.4), (6.6) and (7.49), suggests that the efficiency does improve with $\lambda $ for larger values of this parameter (figure 8).

Figure 8. Period-averaged thrust $- {F_x}$ (a), power P (b) and lift ${F_{y^{\prime}}}$ (c), and the propulsion efficiency, $\eta ={-} \langle {F_x}\rangle /\langle P\rangle $ (d), as functions of $\lambda $. Points mark numerical simulations; ‘exact’ theory, based on (6.2)–(6.4), (6.6) and (7.49), is represented by solid lines; approximations based on (7.46)–(7.48) are dashed. Simulation details are those of case 4 in table 1.

In view of relative insensitivity of the propulsion efficiency on $\lambda $, one can ask why the yellow-bellied sea snake has developed the dorso-ventral asymmetry and swims with its body inclined relative to the swimming direction (Graham et al. 1987). There is no definite answer at this stage. A possible explanation can come from the need to generate hydrodynamic lift to compensate for hydrostatic imbalance. In fact, because $\langle {F_{y^{\prime}}}\rangle $ is a negative definite, whereas $\langle {F_x}\rangle $ is not, their ratio,

(7.52)\begin{equation}\frac{{\langle {F_{y^{\prime}}}\rangle }}{{\langle {F_x}\rangle }} ={-} \int_0^{{x_t}} {\frac{{{{(\omega - k)}^2}{\zeta ^2}(x) + {{\dot{\zeta }}^2}(x)}}{{{\omega ^2} - {k^2} - {{\dot{\zeta }}^2}({x_t})}}\,\textrm{d}\kern0.06em x} + \ldots ,\end{equation}

is, in principle, unbounded – even with no companion torsional deformation wave.

Another explanation is suggested by the averages

(7.53)\begin{gather}- \langle {f_{x^{\prime}}}\rangle = \frac{\rm \pi}{2}\left( {\frac{\textrm{d}}{{\textrm{d}\kern0.06em x}} + \tan \lambda } \right)\Bigg\langle {{{\left( {\frac{{\partial {z_0}}}{{\partial t}}} \right)}^2} - {{\left( {\frac{{\partial {z_0}}}{{\partial x}}} \right)}^2}} \Bigg\rangle + \ldots ,\end{gather}

(7.54)\begin{gather}\langle \iota \rangle = {\rm \pi}\left( {\frac{\textrm{d}}{{\textrm{d}\kern0.06em x}} + \tan \lambda } \right)\left\langle {\frac{{\textrm{D}{z_0}}}{{\textrm{D}t}}\frac{{\partial {z_0}}}{{\partial t}}} \right\rangle + \ldots \end{gather}

of the sectional thrust generated by the aft segment and the sectional power needed to this end. These two expressions follow (5.56) and (5.59) by (7.36), (7.37), (3.6), (3.7) and (5.24). When swimming with $\lambda = 0$, thrust can be generated by the aft segment only through increasing the amplitude of the lateral wave along the body (this is the ‘$\textrm{d}/\textrm{d}\kern0.06em x$’ term). When swimming with $\lambda > 0$, it can be generated with a constant amplitude as well, possibly improving the overall chemo-mechanical efficiency of the swimmer (Iosilevskii 2017).

8. Concluding remarks

8.1. Slender body theory

The agreement between numerical simulations based on the vortex lattice method and the theory implies that no apparent errors were made in the algebraic derivations that led to (5.56)–(5.59), (5.62), (6.2)–(6.4), (6.6), (6.9)–(6.11) and variants thereof. In other words, the theory seems to be coherent in the framework of the potential flow approximation under the particular assumptions made. These assumptions concern the shape of the body, the smallness of the ratio between the lateral and longitudinal length scales of the body–wake configuration and the shape of the wake that the body leaves behind. Indeed, the theory gradually loses its accuracy as $\lambda $ increases, and the slenderness assumption becomes abused. This loss is apparent in figures 5–8. More severe, however, is the loss of accuracy when the assumed shape of the wake footprint in the transverse plane (figure 3a,b) significantly deviates from the actual one (figure 3c,d). An example can be found in figure 9 that shows the same case as in figure 8, but with larger amplitude of the lateral wave. The footprint of the wake in this case looks like that in figure 3(c), and an increase in amplitude increases the width of the wake's ‘s’.

Figure 9. Period-averaged thrust (a) and power (b) as functions of $\lambda $. Solid lines represent the ‘exact’ theory based on (6.2), (6.6) and (7.49); they are the same as in figure 8. Points represent numerical simulation with tail amplitude ${\hat{z}_t}$ from 0.5 (circles, as in figure 8) through 2 (squares) and up to 4 (diamonds). Simulation details are those of cases 4 and 5 in table 1.

Broadly speaking, replacing the actual wake shape by a segment of the y-axis, as was done here, is equivalent to linearization of the boundary conditions in the thin airfoil theory (Ashley & Landahl 1985), and hence can be formally justified only when deviation of the footprint from the respective y-axis is small as compared with the combined length of the body and wake in that plane. Large displacement of the actual wake shape from the assumed one invariably leads to an overestimate of the velocity induced by it, and to an underestimate of the fluid-dynamic forces. Thus said, because the content of the wake is generally non-uniform, there is no way to know a priori when an abuse of the assumptions underlying the present solution renders it unusable for a particular application.

8.2. Applicability limits

Remarks of the previous section concern the validity of the assumptions of the slender body theory within the potential flow approximation, and coherence of algebraic steps that led to its final results. The vortex lattice method cannot be used, of course, to establish the applicability limits of these results. To find them, the verifying standards should be free from any of the assumptions underlying the present results – in particular, thinness of the boundary layer and the wake. In principle, RANS simulations could have been used to generate these standards, but in unsteady cases they are complex and deserve a separate study. A few steady RANS simulations for a wing of finite thickness and the same planform as in figure 11 (Appendix H) can be found in the supplementary material. They practically recover the numerical simulations based on the vortex lattice method.

8.3. Gust response

Aerodynamic loads acting on an oblique wing flying through a non-uniform wind gust were not formally addressed herein. Strictly speaking, the flow field of a non-uniform unidirectional gust is rotational, and violates the assumption of its being otherwise everywhere in the exterior of the boundary layer and the wake. Ignoring this caveat, however – as done in all theoretical studies of gust response (e.g. von Kármán & Sears 1938; Sears 1940) – all equations derived in §§ 4–6 become applicable ‘as is’ to a wing traversing a $z^{\prime}$-directional gust. The only difference is conceptual, as ${w_0}$ and ${w_1}$ become the velocity of the gust at the centreline of the wing and its spanwise gradient.