Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:21:00.623Z Has data issue: false hasContentIssue false
  • English
  • Français

NOTE ON SUMS INVOLVING THE EULER FUNCTION

Part of: Exponential sums and character sums Elementary number theory

Published online by Cambridge University Press:  07 February 2019

SHANE CHERN Open the ORCID record for SHANE CHERN [Opens in a new window]
SHANE CHERN*
Affiliation:
Department of Mathematics, Penn State University, University Park, PA 16802, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note, we provide refined estimates of two sums involving the Euler totient function,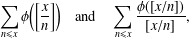

$$\begin{eqnarray}\mathop{\sum }_{n\leq x}\unicode[STIX]{x1D719}\biggl(\biggl[\frac{x}{n}\biggr]\biggr)\quad \text{and}\quad \mathop{\sum }_{n\leq x}\frac{\unicode[STIX]{x1D719}([x/n])}{[x/n]},\end{eqnarray}$$
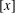where $[x]$ denotes the integral part of real $x$. The above summations were recently considered by Bordellès et al. [‘On a sum involving the Euler function’, Preprint, 2018, arXiv:1808.00188] and Wu [‘On a sum involving the Euler totient function’, Preprint, 2018, hal-01884018].

Keywords

Euler totient functionintegral partasymptotic behaviour

MSC classification

Primary: 11A25: Arithmetic functions; related numbers; inversion formulas
Secondary: 11L07: Estimates on exponential sums
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 194 - 200
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Apostol, T. M., Introduction to Analytic Number Theory, Undergraduate Texts in Mathematics (Springer, New York–Heidelberg, 1976).Google Scholar
Bordellès, O., Arithmetic Tales, translated from the French by Véronique Bordellès, Universitext (Springer, London, 2012).Google Scholar
Bordellès, O., Dai, L., Heyman, R., Pan, H. and Shparlinski, I. E., ‘On a sum involving the Euler function’, Preprint, 2018, arXiv:1808.00188.10.1016/j.jnt.2019.01.006Google Scholar
Hardy, G. H., ‘On Dirichlet’s divisor problem’, Proc. Lond. Math. Soc. (2) 15 (1916), 1–25.Google Scholar
Huxley, M. N., ‘Exponential sums and lattice points. III’, Proc. Lond. Math. Soc. (3) 87(3) (2003), 591–609.Google Scholar
Vaaler, J. D., ‘Some extremal functions in Fourier analysis’, Bull. Amer. Math. Soc. (N.S.) 12(2) (1985), 183–216.Google Scholar
Wu, J., ‘On a sum involving the Euler totient function’, Preprint, 2018, available at hal-01884018.Google Scholar
Wu, J., ‘Note on a paper by Bordellès, Dai, Heyman, Pan and Shparlinski’, Period. Math. Hungar., to appear.Google Scholar