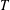 $T$-GAIN SPECTRA
$T$-GAIN SPECTRA
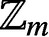 $\mathbb {Z}_m$
WITH IDENTICAL REPRESENTATION FUNCTION
$\mathbb {Z}_m$
WITH IDENTICAL REPRESENTATION FUNCTION
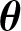 $\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
$\boldsymbol{\theta} $-CONGRUENT NUMBERS OVER REAL NUMBER FIELDS
 $q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
$q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE