Research Article
Cocompactness in algebra and topology
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 385-389
-
- Article
-
- You have access
- Export citation
The solutions to two problems on permutational products
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 390-394
-
- Article
-
- You have access
- Export citation
Lattice properties of the symmetric weakly inverse semigroup on a totally ordered set
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 395-404
-
- Article
-
- You have access
- Export citation
On the behaviour near the boundary of solutions of a semi-linear partial differential equation of elliptic type
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-414
-
- Article
-
- You have access
- Export citation
Division theorems for inverse and pseudo-inverse semigroups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-420
-
- Article
-
- You have access
- Export citation
Almost locally connected spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-428
-
- Article
-
- You have access
- Export citation
Terminal path numbers for certain families of trees
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 429-438
-
- Article
-
- You have access
- Export citation
The asymmetric product of three inhomogeneous linear forms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 439-455
-
- Article
-
- You have access
- Export citation
Intersections of tangent convex curves
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 456-458
-
- Article
-
- You have access
- Export citation
Extensions of a problem of Paul Erdös on groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 459-463
-
- Article
-
- You have access
- Export citation
Finite varieties and groups with Sylow p-subgroups of low class
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 464-469
-
- Article
-
- You have access
- Export citation
Boundary behaviour of meromorphic functions along Green's lines
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 470-474
-
- Article
-
- You have access
- Export citation
The spectrum of skew Room squares
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 475-480
-
- Article
-
- You have access
- Export citation
A generalization of Sperner's theorem
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 481-485
-
- Article
-
- You have access
- Export citation
Discrete groups whose multiplier representations are type I
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 486-495
-
- Article
-
- You have access
- Export citation
Degree-free bounds for dependence relations
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 496-507
-
- Article
-
- You have access
- Export citation
On characters of height zero
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 508-510
-
- Article
-
- You have access
- Export citation
Index
Index
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 511-512
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 31 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 31 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

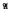 = (
= (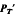 be the set of α ∈
be the set of α ∈