Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T07:59:23.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice properties of the symmetric weakly inverse semigroup on a totally ordered set

Part of: Semigroups Ordered structures

Published online by Cambridge University Press:  09 April 2009

C. C. Edwards  and
Marlow Anderson
C. C. Edwards
Affiliation:
Department of Mathematical Sciences, Indiana University-Purdue University at Fort Wayne Fort Wayne, Indiana 46805, U.S.A.
Marlow Anderson
Affiliation:
Department of Mathematical Sciences, Indiana University-Purdue University at Fort Wayne Fort Wayne, Indiana 46805, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T be a totally ordered set, PT the semigroup of partial transformations on T, and A(T) the l-group of order-preserving permutations of T. We show that PT is a regular left l-semigroup. Let 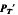be the set of α ∈ PT such that α is order-preserving and the domain of α is a final segment of T. Then 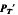is an l-semigroup, and we prove that it is the largest transitive l-subsemigroup of PT which contains A(T). When T is Dedekind complete, we characterize the largest regular l-semigroup of 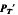. When A(T) is also 0 − 2 transitive we show that there can be no l-subsemigroup of 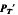properly containing A(T) which is either inverse or a union of groups.

MSC classification

Secondary: 20M20: Semigroups of transformations, etc. 06F05: Ordered semigroups and monoids
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 31 , Issue 4 , December 1981 , pp. 395 - 404
Copyright
Copyright © Australian Mathematical Society 1981

References

Anderson, M. E. and Edwards, C. C. (1980), ‘Unions of l-groups’, to appear.Google Scholar
Bigard, A., Keimel, K. and Wolfenstein, S. (1977), Groupes et anneaux reticules (Springer-Verlag, Berlin).CrossRefGoogle Scholar
Clifford, A. H. (1975), ‘The fundamental representation of a regular semigroup’, Semigroup Forum 10, 84–92.CrossRefGoogle Scholar
Clifford, A. H. and Preston, G. B. (1961), The algebraic theory of semigroups (American Math. Soc., Providence).Google Scholar
Conrad, P. (1970), Lattice-ordered groups (Tulane Library, New Orleans).Google Scholar
Edwards, C. C. (1979), ‘The structure of -unipotent semigroups’, Semigroup Forum 18, 189–199.CrossRefGoogle Scholar
Funchs, L. (1966), Teilweise geordnete algebraische Strukturen (Vandenhoeck and Ruprecht, Gottingen).Google Scholar
Glass, A. M. W. (1976), Ordered permutation groups (Bowling Green State University, Bowling Green, Ohio).Google Scholar
Holland, W. C. (1963), ‘The lattice-ordered group of automorphisms of an ordered set’, Michigan Math. J. 10, 399–408.CrossRefGoogle Scholar
Munn, W. D. (1970), ‘Fundamental inverse semigroups’, Quart. J. Math. Oxford Ser. 21, 157–170.CrossRefGoogle Scholar
Nambooripad, K. S. S. (1973), Structure of regular semigroups (Dissertation, Univ. of Kerala, India).Google Scholar
Srinivasan, B. R. (1968), ‘Weakly inverse semigroups’, Math. Ann. 176, 324–333.CrossRefGoogle Scholar