Research Article
Flat functors and free exact categories
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-156
-
- Article
-
- You have access
- Export citation
Generalized theorem of Hartman-Grobman on measure chains
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-191
-
- Article
-
- You have access
- Export citation
Franel integrals of order four
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 192-203
-
- Article
-
- You have access
- Export citation
Discrete C*-coactions and C*-algebraic bundles
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 204-221
-
- Article
-
- You have access
- Export citation
Locally graded groups with all subgroups normal-by-finite
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 222-227
-
- Article
-
- You have access
- Export citation
On irregularities of distribution III
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 228-244
-
- Article
-
- You have access
- Export citation
Coefficients of an analytic function subordination class determined by rotations
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 245-254
-
- Article
-
- You have access
- Export citation
A group variety defined by a semigroup law
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 255-259
-
- Article
-
- You have access
- Export citation
On the eigenvalues of Redheffer's matrix, II
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 260-273
-
- Article
-
- You have access
- Export citation
Some examples related to Kato's conjecture
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 274-286
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 60 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 60 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

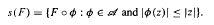
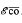
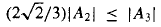 for
for 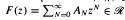 . We also prove that if
. We also prove that if 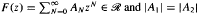 , then
, then  *
*