Admissible rules are shown to be conservatively preserved by the meet-combination of a wide class of logics. A basis is obtained for the resulting logic from bases given for the component logics, under mild conditions. A weak form of structural completeness is proved to be preserved by the combination. Decidability of the set of admissible rules is also shown to be preserved, with no penalty on the time complexity. Examples are provided for the meet-combination of intermediate and modal logics.

In this paper I argue that negation in The Port Royal Logic is not a failed or incoherent approximation of Boolean complementation as maintained by Sylvain Auroux and Marc Dominicy, but is rather a version of privative negation from medieval logic, and that as such it has a perfectly coherent semantics. The discussion reviews the critiques of Auroux and Dominicy as well as the semantics of privative negation as found in Aristotle, Proclus, Ockham, Buridan, Descartes, and Arnauld.

The Generales Inquisitiones de Analysi Notionum et Veritatum is Leibniz’s most substantive work in the area of logic. Leibniz’s central aim in this treatise is to develop a symbolic calculus of terms that is capable of underwriting all valid modes of syllogistic and propositional reasoning. The present paper provides a systematic reconstruction of the calculus developed by Leibniz in the Generales Inquisitiones. We investigate the most significant logical features of this calculus and prove that it is both sound and complete with respect to a simple class of enriched Boolean algebras which we call auto-Boolean algebras. Moreover, we show that Leibniz’s calculus can reproduce all the laws of classical propositional logic, thus allowing Leibniz to achieve his goal of reducing propositional reasoning to algebraic reasoning about terms.

A semantics for quantified modal logic is presented that is based on Kleene’s notion of realizability. This semantics generalizes Flagg’s 1985 construction of a model of a modal version of Church’s Thesis and first-order arithmetic. While the bulk of the paper is devoted to developing the details of the semantics, to illustrate the scope of this approach, we show that the construction produces (i) a model of a modal version of Church’s Thesis and a variant of a modal set theory due to Goodman and Scedrov, (ii) a model of a modal version of Troelstra’s generalized continuity principle together with a fragment of second-order arithmetic, and (iii) a model based on Scott’s graph model (for the untyped lambda calculus) which witnesses the failure of the stability of nonidentity.

This paper is a continuation of Amidei, Pianigiani, San Mauro, Simi, & Sorbi (2016), where we have introduced the quasidialectical systems, which are abstract deductive systems designed to provide, in line with Lakatos’ views, a formalization of trial and error mathematics more adherent to the real mathematical practice of revision than Magari’s original dialectical systems. In this paper we prove that the two models of deductive systems (dialectical systems and quasidialectical systems) have in some sense the same information content, in that they represent two classes of sets (the dialectical sets and the quasidialectical sets, respectively), which have the same Turing degrees (namely, the computably enumerable Turing degrees), and the same enumeration degrees (namely, the 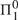${\rm{\Pi }}_1^0$ enumeration degrees). Nonetheless, dialectical sets and quasidialectical sets do not coincide. Even restricting our attention to the so-called loopless quasidialectical sets, we show that the quasidialectical sets properly extend the dialectical sets. As both classes consist of 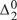${\rm{\Delta }}_2^0$ sets, the extent to which the two classes differ is conveniently measured using the Ershov hierarchy: indeed, the dialectical sets are ω-computably enumerable (close inspection also shows that there are dialectical sets which do not lie in any finite level; and in every finite level n ≥ 2 of the Ershov hierarchy there is a dialectical set which does not lie in the previous level); on the other hand, the quasidialectical sets spread out throughout all classes of the hierarchy (close inspection shows that for every ordinal notation a of a nonzero computable ordinal, there is a quasidialectical set lying in 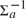${\rm{\Sigma }}_a^{ - 1}$ , but in none of the preceding levels).

This paper suggests that time could have a much richer mathematical structure than that of the real numbers. Clark & Read (1984) argue that a hypertask (uncountably many tasks done in a finite length of time) cannot be performed. Assuming that time takes values in the real numbers, we give a trivial proof of this. If we instead take the surreal numbers as a model of time, then not only are hypertasks possible but so is an ultratask (a sequence which includes one task done for each ordinal number—thus a proper class of them). We argue that the surreal numbers are in some respects a better model of the temporal continuum than the real numbers as defined in mainstream mathematics, and that surreal time and hypertasks are mathematically possible.