Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T21:04:34.086Z Has data issue: false hasContentIssue false
  • English
  • Français

TRIAL AND ERROR MATHEMATICS II: DIALECTICAL SETS AND QUASIDIALECTICAL SETS, THEIR DEGREES, AND THEIR DISTRIBUTION WITHIN THE CLASS OF LIMIT SETS

Published online by Cambridge University Press:  17 October 2016

JACOPO AMIDEI ,
DUCCIO PIANIGIANI ,
LUCA SAN MAURO  and
ANDREA SORBI
JACOPO AMIDEI*
Affiliation:
Scuola Normale Superiore
DUCCIO PIANIGIANI*
Affiliation:
Università Degli Studi di Siena
LUCA SAN MAURO*
Affiliation:
Vienna University of Technology
ANDREA SORBI*
Affiliation:
Università Degli Studi di Siena
*
*SCUOLA NORMALE SUPERIORE I-56126 PISA, ITALY E-mail: [email protected]
† DIPARTIMENTO DI INGEGNERIA INFORMATICA E SCIENZE MATEMATICHE UNIVERSITÀ DEGLI STUDI DI SIENA I-53100 SIENA, ITALY E-mail: [email protected]
‡ INSTITUTE FOR DISCRETE MATHEMATICS AND GEOMETRY VIENNA UNIVERSITY OF TECHNOLOGY 1040 WIEN, AUSTRIA E-mail: [email protected]
§ DIPARTIMENTO DI INGEGNERIA INFORMATICA E SCIENZE MATEMATICHE UNIVERSITÀ DEGLI STUDI DI SIENA I-53100 SIENA, ITALY E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is a continuation of Amidei, Pianigiani, San Mauro, Simi, & Sorbi (2016), where we have introduced the quasidialectical systems, which are abstract deductive systems designed to provide, in line with Lakatos’ views, a formalization of trial and error mathematics more adherent to the real mathematical practice of revision than Magari’s original dialectical systems. In this paper we prove that the two models of deductive systems (dialectical systems and quasidialectical systems) have in some sense the same information content, in that they represent two classes of sets (the dialectical sets and the quasidialectical sets, respectively), which have the same Turing degrees (namely, the computably enumerable Turing degrees), and the same enumeration degrees (namely, the 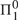${\rm{\Pi }}_1^0$ enumeration degrees). Nonetheless, dialectical sets and quasidialectical sets do not coincide. Even restricting our attention to the so-called loopless quasidialectical sets, we show that the quasidialectical sets properly extend the dialectical sets. As both classes consist of 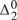${\rm{\Delta }}_2^0$ sets, the extent to which the two classes differ is conveniently measured using the Ershov hierarchy: indeed, the dialectical sets are ω-computably enumerable (close inspection also shows that there are dialectical sets which do not lie in any finite level; and in every finite level n ≥ 2 of the Ershov hierarchy there is a dialectical set which does not lie in the previous level); on the other hand, the quasidialectical sets spread out throughout all classes of the hierarchy (close inspection shows that for every ordinal notation a of a nonzero computable ordinal, there is a quasidialectical set lying in 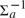${\rm{\Sigma }}_a^{ - 1}$ , but in none of the preceding levels).

Type
Research Article
Information
The Review of Symbolic Logic , Volume 9 , Issue 4 , December 2016 , pp. 810 - 835
Copyright
Copyright © Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Amidei, J., Pianigiani, D., San Mauro, L., Simi, G., & Sorbi, A. (2016). Trial and error mathematics I: Dialectical and quasidialectical systems. Review of Symbolic Logic, 9(2), 299–324.Google Scholar
Ash, C. J. & Knight, J. (2000). Computable Structures and the Hyperarithmetical Hierarchy. Studies in Logic and the Foundations of Mathematics, Vol. 144. Amsterdam: Elsevier.Google Scholar
Bernardi, C. (1974). Aspetti ricorsivi degli insiemi dialettici. Bollettino della Unione Matematica Italiana, Series IV, 9, 51–61.Google Scholar
Cooper, S. B. (2003). Computability Theory. Boca Raton, London, New York, Washington, DC: Chapman & Hall/CRC Mathematics.Google Scholar
Ershov, Yu. L. (1968a). A hierarchy of sets, I. Algebra and Logic, 7(1), 25–43.CrossRefGoogle Scholar
Ershov, Yu. L. (1968b). A hierarchy of sets, II. Algebra and Logic, 7(4), 212–232.Google Scholar
Ershov, Yu. L. (1970). A hierarchy of sets, III. Algebra and Logic, 9(1), 20–31.CrossRefGoogle Scholar
Jockusch, C. G Jr.. (1974). ${\rm{\Pi }}_1^0$ classes and Boolean combinations of recursively enumerable sets. The Journal of Symbolic Logic, 39(1), 95–96.CrossRefGoogle Scholar
Magari, R. (1974). Su certe teorie non enumerabili. Annali di Matematica Pura ed Applicata, Series IV, XCVIII, 119–152.Google Scholar
Nies, A. (2009). Computability and Randomness. Oxford: Oxford University Press.Google Scholar
Ospichev, S. (2014). Friedberg numberings in the Ershov hierarchy. Algebra and Logic, 54(4), 283–295.Google Scholar
Rogers, H Jr.. (1967). Theory of Recursive Functions and Effective Computability. New York: McGraw-Hill.Google Scholar
Schmerl, J. H. (2005). Undecidable theories and reverse mathematics. In Simpson, S. G., editor. Reverse Mathematics 2001. Lecture Notes in Logic, Vol. 21. La Jolla, CA: Association for Symbolic Logic, pp. 349–351.Google Scholar
Soare, R. I. (1987). Recursively Enumerable Sets and Degrees. Perspectives in Mathematical Logic, Omega Series. Heidelberg: Springer-Verlag.Google Scholar