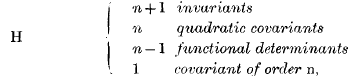Proceedings of the Royal Society of Edinburgh, Volume 45 - Issue 2 - 1926
- This volume was published under a former title. See this journal's title history.
Proceedings
XII.—A Survey of Clyde Plankton
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 117-141
-
- Article
- Export citation
XIII.—The Relation of Sea-Growth and Spawning Frequency in Salmo salar
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 142-148
-
- Article
- Export citation
XIV.—The Minimum System of Two Quadratic Forms in n Variables
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 149-165
-
- Article
- Export citation
XV.—The Law of Blackening of the Photographic Plate at Low Densities
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 166-186
-
- Article
- Export citation
XVI.—The Theory of Compound Determinants from 1900 to 1920
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 187-212
-
- Article
- Export citation
XVII.—Discontinuities in the Atmosphere
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. 213-229
-
- Article
- Export citation
Front matter
PRE volume 45 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. f1-f8
-
- Article
-
- You have access
- Export citation
Back matter
PRE volume 45 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 15 September 2014, pp. b1-b4
-
- Article
-
- You have access
- Export citation