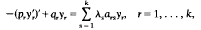Research Article
Nonlinear dynamical theory of the elastica
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 1-23
-
- Article
- Export citation
L∞-continuity of Henkin operators solving
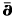 in certain weakly pseudoconvex domains of ℂ2
in certain weakly pseudoconvex domains of ℂ2
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 25-33
-
- Article
- Export citation
The distance between unitary orbits of normal elements in the Calkin algebra
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 35-43
-
- Article
- Export citation
A weighted norm inequality for the Hankel transformation
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 45-50
-
- Article
- Export citation
Asymptotics of Sturm-Liouville eigenvalues for problems on a finite interval with one limit-circle singularity, I*
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 51-70
-
- Article
- Export citation
Exact estimates of conductivity of composites formed by two isotropically conducting media taken in prescribed proportion
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 71-87
-
- Article
- Export citation
Comparison functions for a model problem related to nonlinear elasticity
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 89-114
-
- Article
- Export citation
Level and index in the modular group
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 115-126
-
- Article
- Export citation
Boundary value conditions for wave fronts in reaction-diffusion systems
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 127-136
-
- Article
- Export citation
Multipliers for vector valued functions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 137-143
-
- Article
- Export citation
On regular semigroup rings
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 145-151
-
- Article
- Export citation
Inverse semigroups generated by nilpotent transformations
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 153-162
-
- Article
- Export citation
K-analytic uniform structures
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 163-170
-
- Article
- Export citation
Balanced big Cohen-Macaulay modules and ring extensions
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 171-172
-
- Article
- Export citation
Multiparameter Sturm theory
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 173-184
-
- Article
- Export citation
RP-dominated regular semigroups
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 185-191
-
- Article
- Export citation
Sums and products of quasi-nilpotent operators
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. 193-200
-
- Article
- Export citation
Front matter
PRM volume 99 issue 1-2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PRM volume 99 issue 1-2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 14 November 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation

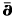 in certain weakly pseudoconvex domains of ℂ
in certain weakly pseudoconvex domains of ℂ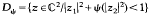
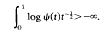
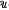 (s) denote the unitary orbit of
(s) denote the unitary orbit of 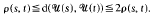
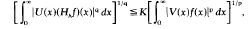
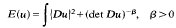
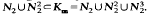 is also proved.
is also proved.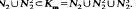
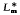 of L
of L