Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-25T20:15:59.201Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse semigroups generated by nilpotent transformations

Published online by Cambridge University Press:  14 November 2011

John M. Howie  and
M. Paula O. Marques-Smith
John M. Howie
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews, Fife KY16 9SS
M. Paula O. Marques-Smith
Affiliation:
Area de Matematica, Universidade do Minho, 4700 Braga, Portugal
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be a set with infinite cardinality m and let B be the Baer-Levi semigroup, consisting of all one-one mappings a:X→X for which ∣X/Xα∣ = m. Let Km=<B 1B>, the inverse subsemigroup of the symmetric inverse semigroup ℐ(X) generated by all products β−γ, with β,γ∈B. Then Km = <N2>, where N2 is the subset of ℐ(X) consisting of all nilpotent elements of index 2. Moreover, Km has 2-nilpotent-depth 3, in the sense that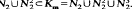

Let Pm be the ideal {α∈Km: ∣dom α∣<m} in Km and let Lm be the Rees quotient Km/Pm. Then Lm is a 0-bisimple, 2-nilpotent-generated inverse semigroup with 2-nilpotent-depth 3. The minimum non-trivial homomorphic image 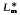of Lm also has these properties and is congruence-free.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 99 , Issue 1-2 , 1984 , pp. 153 - 162
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Baer, R. and Levi, F.. Vollständige irreduzibele Systeme von Gruppenaxiomen. (Beitrage zur Algebra, No. 18) Sitzungsber. Heidelb. Akad. Wiss. Abh. 2 (1932), 1–12.Google Scholar
2Clifford, A. H. and Preston, G. B.. The algebraic theory of semigroups, vols. 1 and 2 (Providence, R.I.: American Math. Soc, 1961 and 1967).Google Scholar
3Howie, J. M.. An introduction to semigroup theory (London: Academic Press, 1976).Google Scholar
4Howie, J. M.. A class of bisimple idempotent-generated congruence-free semigroups. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 169–184.Google Scholar
5Liber, A. E.. On symmetric generalized groups. Mat. Sb. 33 (75) (1953), 531–544 (in Russian).Google Scholar
6Lindsey, D. and Madison, B.. The lattice of congruences on a Baer-Levi semigroup. Semigroup Forum 12 (1976), 63–70.Google Scholar
7Marques, M. Paula O.. A congruence-free semigroup associated with an infinite cardinal number. Proc. Roy. Soc. Edinburgh Sect. A 93 (1983), 245–257.Google Scholar
8Marques, M. Paula O.. Infinite transformation semigroups (Ph.D. Thesis, University of St Andrews, 1983).Google Scholar
9Schein, B.M.. Homomorphisms and subdirect decomposition of semigroups. Pacific J. Math. 17 (1966), 529–547.Google Scholar
10Trotter, P. G.. Congruence-free regular semigroups with zero. Semigroup Forum 12 (1976), 1–5.Google Scholar