No CrossRef data available.
Article contents
Comparison functions for a model problem related to nonlinear elasticity
Published online by Cambridge University Press: 14 November 2011
Extract
Comparison functions are constructed for the problem of minimizing
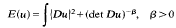
over maps u: D(⊆ℝ2)→ℝ2 with det≥0, subject to the constraint u= f on ∂D, D the unit disk. This is accomplished for maps / which are reparameterizations of ∂D or which are “graph-like” maps. Estimates involving half derivative boundary norms are obtained.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 99 , Issue 1-2 , 1984 , pp. 89 - 114
- Copyright
- Copyright © Royal Society of Edinburgh 1984
References
1Ball, J. M.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Rational Mech. Anal 63 (1977), 337–403.CrossRefGoogle Scholar
2Ball, J. M.. Global invertibility of Sobelov functions and the interpenetration of matter. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 315–328.CrossRefGoogle Scholar
3Giaquinta, M.. Multiple integrals in the calculus of variations and nonlinear elliptic systems (Princeton, N.J.: Princeton University Press, 1983).Google Scholar
4Malek-Madani, R. and Smith, P. D.. Regularity theorem for minimizers of a nonconvex functional. J. Math. Phys. submitted.Google Scholar
5Muckenhoupt, B. and Wheeden, R. L.. Weighted norm inequalities for fractional integrals. Trans. Amer. Math. Soc. 192 (1974), 261–274.CrossRefGoogle Scholar
6Necas, J.. Les methodes directes en theorie des equations elliptiques (Prague: Academia - Editions de l'Academie Tchecoslovaque des Sciences, 1967).Google Scholar
7Stredulinsky, E. W.. Higher integrability from reverse Holder inequalities. Indiana Univ. Math. J. 29 (1980) 407–413.CrossRefGoogle Scholar
8Stein, E. M. and Weiss, G.. Introduction to Fourier analysis on Euclidean spaces. (Princeton, N.J.: Princeton Univ. Press, 1971).Google Scholar


