Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-10T07:48:47.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Some nonexistence theorems for semilinear fourth-order equations

Part of: Partial differential equations

Published online by Cambridge University Press:  27 December 2018

M. Á. Burgos-Pérez ,
J. García-Melián  and
A. Quaas
M. Á. Burgos-Pérez
Affiliation:
Departamento de Análisis Matemático, Universidad de La Laguna, C/. Astrofísico Francisco Sánchez s/n, 38200 La Laguna, Spain ([email protected])
J. García-Melián
Affiliation:
Departamento de Análisis Matemático, Universidad de La Laguna, C/. Astrofísico Francisco Sánchez s/n, 38200 La Laguna, Spainand Instituto Universitario de Estudios Avanzados (IUdEA) en Física Atómica, Molecular y Fotónica, Universidad de La Laguna, C/. Astrofísico Francisco Sánchez s/n, 38200 La Laguna, Spain ([email protected])
A. Quaas
Affiliation:
Departamento de Matemática,Universidad Técnica Federico Santa María, Casilla V-110, Avda. España, 1680 Valparaíso, Chile ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we analyse the semilinear fourth-order problem ( − Δ)2u = g(u) in exterior domains of ℝN. Assuming the function g is nondecreasing and continuous in [0, + ∞) and positive in (0, + ∞), we show that positive classical supersolutions u of the problem which additionally verify − Δu > 0 exist if and only if N ≥ 5 and

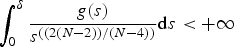$$\int_0^\delta \displaystyle{{g(s)}\over{s^{(({2(N-2)})/({N-4}))}}} {\rm d}s \lt + \infty$$
for some δ > 0. When only radially symmetric solutions are taken into account, we also show that the monotonicity of g is not needed in this result. Finally, we consider the same problem posed in ℝN and show that if g is additionally convex and lies above a power greater than one at infinity, then all positive supersolutions u automatically verify − Δu > 0 in ℝN, and they do not exist when the previous condition fails.

Keywords

Liouville theoremsmaximum principleelliptic systems

MSC classification

Primary: 35B53: Liouville theorems, Phragmén-Lindelöf theorems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 3 , June 2019 , pp. 761 - 779
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alarcón, S., García-Melián, J. and Quaas, A.. Optimal Liouville theorems for supersolutions of elliptic equations with the Laplacian. Ann. Scuola Norm. Sup. Pisa. XVI (2016), 129–158.Google Scholar
2Caristi, G., D'Ambrosio, L. and Mitidieri, E.. Representation formulae for solutions to some classes of higher order systems and related Liouville theorems. Milan J. Math. 76 (2008), 27–67.Google Scholar
3Dávila, J., Dupaigne, L., Wang, K. and Wei, J.. A monotonicity formula and a Liouville-type theorem for a fourth order supercritical problem. Adv. Math. 258 (2014), 240–285.Google Scholar
4De Figueiredo, D. and Mitidieri, E.. Maximum principles for linear elliptic systems. Rend. Istit. Mat. Univ. Trieste 22 (1990), 36–66.Google Scholar
5Gazzola, F. and Grunau, H. C.. Radial entire solutions for supercritical biharmonic equations. Math. Ann. 334 (2006), 905–936.Google Scholar
6Guo, Y. and Liu, J.. Liouville-type theorems for polyharmonic equations in ℝN and in ${\open R}^N_+$. Proc. Royal Soc. Ed. 138A (2008), 339–359.Google Scholar
7Hu, L. G.. Liouville-type theorems for the fourth order nonlinear elliptic equation. J. Differ. Equ. 256 (2014), 1817–1846.Google Scholar
8Lin, C. S.. A classification of solutions of a conformally invariant fourth order equation in ℝn. Comment. Math. Helv. 73 (1998), 206–231.Google Scholar
9Mitidieri, E.. A Rellich type identity and applications. Comm. Partial Differ. Equ. 18 (1993), 125–151.Google Scholar
10Mitidieri, E.. Nonexistence of positive solutions of semilinear elliptic systems in ℝN. Differ. Integral Equ. 9 (1996), 465–479.Google Scholar
11Mitidieri, E. and Pohozaev, S.. A priori estimates and the absence of solutions of nonlinear partial differential equations and inequalities. Tr. Mat. Inst. Steklova 234 (2001), 1–384. English translation in Proc. Steklov Inst. Math. 2001, no. 3 (234), 1–362.Google Scholar
12Pao, C. V.. Nonlinear parabolic and elliptic equations (New York: Plenum Press, 1992).Google Scholar
13Wei, J. C. and Xu, X. W.. Classification of solutions of higher order conformally invariant equations. Math. Ann. 313 (1999), 207–228.Google Scholar
14Wei, J. C. and Ye, D.. Liouville theorems for stable solutions of biharmonic problem. Math. Ann. 356 (2013), 1599–1612.Google Scholar