Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T19:49:59.425Z Has data issue: false hasContentIssue false
  • English
  • Français

On integral transforms whose kernels are solutions of singular Sturm–Liouville problems

Published online by Cambridge University Press:  14 November 2011

Ahmed I. Zayed
Ahmed I. Zayed
Affiliation:
Mathematics Department, California Polytechnic State University, San Luis Obispo, CA 93407, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we investigate integral transforms of type 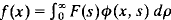, where φ(x, s) is the solution of the singular Sturm–Liouville problem: y″ + (s2 – q(x))y = 0, 0≦x <∞ with y(0) cos α + y′(0)sin α = 0, y(x) is bounded at ∞, and dp is the spectral measure. If F(s) = sk for some k = 0, 1, 2, …, then f(x) may not exist since, in general, φ(x, s) is not even in 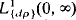. One aim of this paper is to investigate the Abel summability of these integrals. In the special case where q(x) = 0 and α = π/2, then φ(x, s) = cos sx and dp = ds, while if α = 0, then φ(x, s) = −sin sx/s and dp = s2ds. It is known that

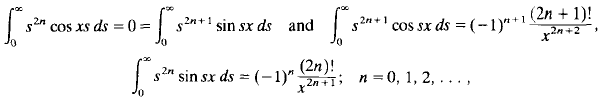
where the values of these integrals are interpreted as the Abel limits of these integrals or as the Fourier transform of some tempered distributions. Another aim of this paper is to derive the analogue of these results for the general kernel φ(x, s), and then apply that to the theory of asymptotic expansions.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 108 , Issue 3-4 , 1988 , pp. 201 - 228
Copyright
Copyright © Royal Society of Edinburgh 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Diamond, H., Kon, M. and Raphael, L.. Stable summation methods for a class of singular Sturm-Liouville expansions. Proc. Amer. Math. Soc. 81 (1981), 279–286.CrossRefGoogle Scholar
2Grosjean, C.. On the series expansion of certain types of Fourier integrals in the neighborhood of the origin. Bull. Soc. Math. Belg. Ser. A 17 (1965), 251–418.Google Scholar
3Handelsman, R. and Lew, J.. Asymptotic expansion of a class of integral transforms via Mellin transforms. Arch. Rational Mech. Anal. 35 (1969), 382–396.CrossRefGoogle Scholar
4Hardy, G.. Divergent series (London: Oxford University Press (Clarendon), 1949).Google Scholar
5Hille, E.. Lectures on ordinary differential equations (New York: Addison-Wesley, 1969).Google Scholar
6Levin, J.. Distribution of zeros of entire functions. Transl. Math. Monographs 5 (Providence, R.I.: American Mathematical Society, 1964).Google Scholar
7Levitan, B. and Sargsjan, I.. Introduction to spectral theory. Transl. Math. Monographs 39 (Providence, R. I.: American Mathematical Society, 1975).Google Scholar
8Lighthill, M.. Fourier analysis and generalized functions (London: Cambridge University Press, 1958).Google Scholar
9Olver, F.. Error bounds for stationary phase approximations. SIAM J. Math. Anal. 5 (1974), 19–29.CrossRefGoogle Scholar
10Walter, G. and Zayed, A.. Real singularities of singular Sturm-Liouville expansion. SIAM J. Math. Anal. 18 (1987), 219–227.CrossRefGoogle Scholar
11Wong, R.. Error bounds for asymptotic expansions of integrals. SIAM Rev. 22 (1980), 401–435.CrossRefGoogle Scholar
12Wong, R.. Error bounds for asymptotic expansions of Hankel transforms. SIAM J. Math. Anal. 7 (1976), 799–808.CrossRefGoogle Scholar
13Zemanian, A.. Distribution theory and transform analysis (New York: McGraw Hill, 1965).Google Scholar
14Zayed, A. and Walter, G.. On the singularities of singular Sturm-Liouville expansions and an associated class of elliptic P.D.E.'s. SIAM J. Math. Anal. 18 (1987), 219–227.Google Scholar
15Zayed, A.. Asymptotic expansions of some integral transforms by using generalized functions. Trans. Amer. Math. Soc. 272 (1982), 785–802.CrossRefGoogle Scholar