There is a set of n bandits and at every stage, two of the bandits are chosen to play a game, with the result of a game being learned. In the “weak regret problem,” we suppose there is a “best” bandit that wins each game it plays with probability at least p > 1/2, with the value of p being unknown. The objective is to choose bandits to maximize the number of times that one of the competitors is the best bandit. In the “strong regret problem”, we suppose that bandit i has unknown value vi, i = 1, …, n, and that i beats j with probability vi/(vi + vj). One version of strong regret is interested in maximizing the number of times that the contest is between the players with the two largest values. Another version supposes that at any stage, rather than choosing two arms to play a game, the decision maker can declare that a particular arm is the best, with the objective of maximizing the number of stages in which the arm with the largest value is declared to be the best. In the weak regret problem, we propose a policy and obtain an analytic bound on the expected number of stages over an infinite time frame that the best arm is not one of the competitors when this policy is employed. In the strong regret problem, we propose a Thompson sampling type algorithm and empirically compare its performance with others in the literature.
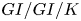 $GI/GI/K$ QUEUE GIVEN PARTIAL INFORMATION
$GI/GI/K$ QUEUE GIVEN PARTIAL INFORMATION