Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T08:11:53.215Z Has data issue: false hasContentIssue false
  • English
  • Français

A MEAN FIELD GAME ANALYSIS OF SIR DYNAMICS WITH VACCINATION

Published online by Cambridge University Press:  13 November 2020

Josu Doncel Open the ORCID record for Josu Doncel [Opens in a new window] ,
Nicolas Gast Open the ORCID record for Nicolas Gast [Opens in a new window]  and
Bruno Gaujal
Josu Doncel
Affiliation:
University of the Basque Country, Leioa48940, Spain E-mail: [email protected]
Nicolas Gast
Affiliation:
INRIA and Université Grenoble Alpes, CNRS, LIG, F-38000Grenoble, France E-mails: [email protected]; [email protected]
Bruno Gaujal
Affiliation:
INRIA and Université Grenoble Alpes, CNRS, LIG, F-38000Grenoble, France E-mails: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyze a mean field game model of SIR dynamics (Susceptible, Infected, and Recovered) where players choose when to vaccinate. We show that this game admits a unique mean field equilibrium (MFE) that consists in vaccinating at a maximal rate until a given time and then not vaccinating. The vaccination strategy that minimizes the total cost has the same structure as the MFE. We prove that the vaccination period of the MFE is always smaller than the one minimizing the total cost. This implies that, to encourage optimal vaccination behavior, vaccination should always be subsidized. 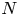Finally, we provide numerical experiments to study the convergence of the equilibrium when the system is composed by a finite number of agents ($N$) to the MFE. These experiments show that the convergence rate of the cost is 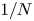$1/N$ and the convergence of the switching curve is monotone.

Keywords

applied probabilityprobabilistic networksstochastic modeling
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 2 , April 2022 , pp. 482 - 499
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, R.M., May, R.M., & Anderson, B. (1992). Infectious diseases of humans: dynamics and control, vol. 28. Hoboken, New Jersey, USA: Wiley Online Library.Google Scholar
Bauch, C.T. & Earn, D.J. (2004). Vaccination and the theory of games. Proceedings of the National Academy of Sciences of the United States of America 101(36): 13391–13394.CrossRefGoogle ScholarPubMed
Bayraktar, E. & Cohen, A. (2017). Analysis of a finite state many player game using its master equation. Preprint arXiv:1707.02648.Google Scholar
Behncke, H. (2000). Optimal control of deterministic epidemics. Optimal Control Applications and Methods 21(6): 269–285.CrossRefGoogle Scholar
Bertsekas, D.P. (1995). Dynamic programming and optimal control, vol. 1. Belmont, MA: Athena Scientific.Google Scholar
Carmona, R., Delarue, F., & Lachapelle, A. (2013). Control of Mckean–Vlasov dynamics versus mean field games. Mathematics and Financial Economics 7(2): 131–166.CrossRefGoogle Scholar
Cecchin, A. & Fischer, M. (2018). Probabilistic approach to finite state mean field games. Applied Mathematics & Optimization 81: 253–300.CrossRefGoogle Scholar
Cecchin, A. & Pelino, G. (2019). Convergence, fluctuations and large deviations for finite state mean field games via the master equation. Stochastic Processes and Their Applications 129(11): 4510–4555.CrossRefGoogle Scholar
Diekmann, O. & eesterbeek, J.A.P. (2000). Mathematical epidemiology of infectious diseases: model building, analysis and interpretation, vol. 5. Hoboken, New Jersey, USA: John Wiley & Sons.Google Scholar
Doncel, J., Gast, N., & Gaujal, B. (2019). Discrete mean field games: existence of equilibria and convergence. Journal of Dynamics and Games 6(3): 1–19.Google Scholar
Francis, P.J. (2004). Optimal tax/subsidy combinations for the flu season. Journal of Economic Dynamics and Control 28(10): 2037–2054.CrossRefGoogle Scholar
Gast, N. (2017). Expected values estimated via mean-field approximation are 1/n-accurate. Proceedings of the ACM on Measurement and Analysis of Computing Systems 1(1): 1–26.Google Scholar
Gast, N. & Houdt, B.V. (2018). A refined mean field approximation. In ACM SIGMETRICS 2018, Irvine, USA, p. 1.CrossRefGoogle Scholar
Geoffard, P.-Y. & Philipson, T. (1997). Disease eradication: private versus public vaccination. The American Economic Review 87(1): 222–230.Google Scholar
Gomes, D.A., Mohr, J., & Souza, R.R. (2010). Discrete time, finite state space mean field games. Journal de Mathématiques Pures et Appliquées 93(3): 308–328.CrossRefGoogle Scholar
Gomes, D.A., Mohr, J., & Souza, R.R. (2013). Continuous time finite state mean field games. Applied Mathematics & Optimization 68(1): 99–143.CrossRefGoogle Scholar
Guéant, O. (2014). Existence and uniqueness result for mean field games with congestion effect on graphs. Applied Mathematics & Optimization 72(2): 291–303.CrossRefGoogle Scholar
Hubert, E. & Turinici, G. (2018). Nash-MFG equilibrium in a SIR model with time dependent newborn vaccination. Ricerche di Matematica 67: 227–246.CrossRefGoogle Scholar
Kermack, W.O. & McKendrick, A.G. (1927). A contribution to the mathematical theory of epidemics. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 115. The Royal Society, pp. 700–721.Google Scholar
Kolokoltsov, V.N., Li, J., & Yang, W. (2011). Mean field games and nonlinear Markov processes. Preprint arXiv:1112.3744.Google Scholar
Laguzet, L. & Turinici, G. (2015). Individual vaccination as Nash equilibrium in a SIR model: the interplay between individual optimization and societal policies. Hal-01100579, version 1. Available at: https://hal.archives-ouvertes.fr/hal-01100579v1.Google Scholar
Laguzet, L. & Turinici, G. (2015). Global optimal vaccination in the sir model: properties of the value function and application to cost-effectiveness analysis. Mathematical Biosciences 263: 180–197.CrossRefGoogle ScholarPubMed
Morton, R. & Wickwire, K.H. (1974). On the optimal control of a deterministic epidemic. Advances in Applied Probability 6(4): 622–635.CrossRefGoogle Scholar
Shapley, L.S. (1953). Stochastic games. Proceedings of the National Academy of Sciences 39(10): 1095–1100.CrossRefGoogle ScholarPubMed
Todorov, E. (2007). Optimal control theory. In Doya, K. (ed.), Bayesian Brain: Probabilistic Approaches to Neural Coding, MIT Press. pp. 269–298.Google Scholar