Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T08:24:28.179Z Has data issue: false hasContentIssue false
  • English
  • Français

ANALYTICAL RESULTS ON THE SERVICE PERFORMANCE OF STOCHASTIC CLEARING SYSTEMS

Published online by Cambridge University Press:  13 November 2020

Bo Wei Open the ORCID record for Bo Wei [Opens in a new window] ,
Sıla Çetinkaya Open the ORCID record for Sıla Çetinkaya [Opens in a new window]  and
Daren B. H. Cline
Bo Wei
Affiliation:
IORA, National University of Singapore, Singapore, Singapore
Sıla Çetinkaya
Affiliation:
Engineering Management, Information, and Systems, Southern Methodist University, Dallas, TX, USA E-mail: [email protected]
Daren B. H. Cline
Affiliation:
Department of Statistics, Texas A&M University College Station, College Station, TX, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Stochastic clearing theory has wide-spread applications in the context of supply chain and service operations management. Historical application domains include bulk service queues, inventory control, and transportation planning (e.g., vehicle dispatching and shipment consolidation). In this paper, motivated by a fundamental application in shipment consolidation, we revisit the notion of service performance for stochastic clearing system operation. More specifically, our goal is to evaluate and compare service performance of alternative operational policies for clearing decisions, as quantified by a measure of timely service referred to as Average Order Delay (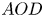$AOD$). All stochastic clearing systems are subject to service delay due to the inherent clearing practice, and 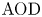$\textrm {AOD}$ can be thought of as a benchmark for evaluating timely service. Although stochastic clearing theory has a long history, the existing literature on the analysis of 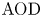$\textrm {AOD}$ as a service measure has several limitations. Hence, we extend the previous analysis by proposing a more general method for a generic analytical derivation of 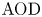$\textrm {AOD}$ for any renewal-type clearing policy, including but not limited to alternative shipment consolidation policies in the previous literature. Our proposed method utilizes a new martingale point of view and lends itself for a generic analytical characterization of 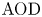$\textrm {AOD}$, leading to a complete comparative analysis of alternative renewal-type clearing policies. Hence, we also close the gaps in the literature on shipment consolidation via a complete set of analytically provable results regarding 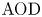$\textrm {AOD}$ which were only illustrated through numerical tests previously.

Keywords

martingalesrenewal-type clearing policiesshipment consolidationstochastic clearing theorytruncated random variables
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 2 , April 2022 , pp. 217 - 236
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K.B. & Lahiri, S.N. (2006). Measure theory and probability theory. New York, NY, USA: Springer Science & Business Media.Google Scholar
Bookbinder, J.H., Cai, Q., & He, Q.-M. (2011). Shipment consolidation by private carrier: the discrete time and discrete quantity case. Stochastic Models 27(4): 664–686.CrossRefGoogle Scholar
Cai, Q., He, Q.M., & Bookbinder, J.H. (2014). A tree-structured Markovian model of the shipment consolidation process. Stochastic Models 30(4): 521–553.CrossRefGoogle Scholar
Çetinkaya, S. (2005). Coordination of inventory and shipment consolidation decisions: a review of premises, models, and justification. In Geunes, J., Akçali, E., Pardalos, P.M., Romejin, H.E., & Shen, Z.J. (eds), Applications of supply chain management and e-commerce research. New York: Springer, pp. 3–51.CrossRefGoogle Scholar
Çetinkaya, S. & Bookbinder, J.H. (2003). Stochastic models for the dispatch of consolidated shipments. Transportation Research Part B: Methodological 37(8): 747–768.CrossRefGoogle Scholar
Çetinkaya, S. & Lee, C.-Y. (2000). Stock replenishment and shipment scheduling for vendor-managed inventory systems. Management Science 46(2): 217–232.CrossRefGoogle Scholar
Çetinkaya, S., Mutlu, F., & Lee, C.-Y. (2006). A comparison of outbound dispatch policies for integrated inventory and transportation decisions. European Journal of Operational Research 171(3): 1094–1112.CrossRefGoogle Scholar
Çetinkaya, S., Tekin, E., & Lee, C.-Y. (2008). A stochastic model for joint inventory and outbound shipment decisions. IIE Transactions 40(3): 324–340.CrossRefGoogle Scholar
Çetinkaya, S., Mutlu, F., & Wei, B. (2014). On the service performance of alternative shipment consolidation policies. Operations Research Letters 42(1): 41–47.CrossRefGoogle Scholar
Cook, R.A. & Lodree, E.J. (2017). Dispatching policies for last-mile distribution with stochastic supply and demand. Transportation Research Part E: Logistics and Transportation Review 106: 353–371.CrossRefGoogle Scholar
Economou, A. & Manou, A. (2013). Equilibrium balking strategies for a clearing queueing system in alternating environment. Annals of Operations Research 208(1): 489–514.CrossRefGoogle Scholar
Higginson, J. & Bookbinder, J.H. (1994). Policy recommendations for a shipment-consolidation program. Journal of Business Logistics 15(1): 87–112.Google Scholar
Kaya, O., Kubalı, D., & Örmeci, L. (2013). Stochastic models for the coordinated production and shipment problem in a supply chain. Computers & Industrial Engineering 64(3): 838–849.CrossRefGoogle Scholar
Kella, O., Perry, D., & Stadje, W. (2003). A stochastic clearing model with a Brownian and a compound Poisson component. Probability in the Engineering and Information Sciences 17: 1–22.CrossRefGoogle Scholar
Lai, M., Weili, X., & Zhao, L. (2016). Cost allocation for cooperative inventory consolidation problems. Operations Research Letters 44(6): 761–765.CrossRefGoogle Scholar
Mutlu, F. & Çetinkaya, S. (2010). An integrated model for stock replenishment and shipment scheduling under common carrier dispatch costs. Transportation Research Part E: Logistics and Transportation Review 46(6): 844–854.CrossRefGoogle Scholar
Mutlu, F., Çetinkaya, S., & Bookbinder, J.H. (2010). An analytical model for computing the optimal time-and-quantity-based policy for consolidated shipments. IIE Transactions 42: 367–377.CrossRefGoogle Scholar
Robin, M. & Tapiero, C.S. (1982). A simple vehicle dispatching policy with non-stationary stochastic arrival rates. Transportation Research Part B 16(6): 449–457.CrossRefGoogle Scholar
Ross, S.M. (1969). Optimal dispatching of a Poisson process. Journal of Applied Probability 6: 692–699.CrossRefGoogle Scholar
Ross, S.M. (1996). Stochastic processes, 2nd ed. New York: John Wiley & Sons.Google Scholar
Satır, B., Erenay, F.S., & Bookbinder, J.H. (2018). Shipment consolidation with two demand classes: rationing the dispatch capacity. European Journal of Operational Research 270(1): 171–184.CrossRefGoogle Scholar
Stidham, S. (1974). Stochastic clearing systems. Stochastic Processes and Their Applications 2: 85–113.CrossRefGoogle Scholar
Stidham, S. (1977). Cost models for stochastic clearing systems. Operations Research 25(1): 100–127.CrossRefGoogle Scholar
Tapiero, C.S. & Zuckerman, D. (1979). Vehicle dispatching with competition. Transportation Research Part B 13: 207–216.CrossRefGoogle Scholar
Ülkü, M.A. & Bookbinder, J.H. (2012). Optimal quoting of delivery time by a third party logistics provider: the impact of shipment consolidation and temporal pricing schemes. European Journal of Operational Research 221(1): 110–117.CrossRefGoogle Scholar
Zuckerman, D. & Tapiero, C.S. (1980). Random vehicle dispatching with options and optimal fleet size. Transportation Research Part B 14: 361–368.CrossRefGoogle Scholar