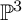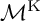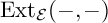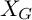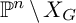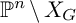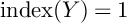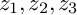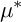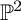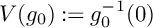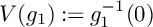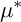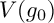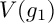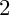Article
NEW MODULI SPACES OF ONE-DIMENSIONAL SHEAVES ON
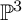 $\mathbb {P}^3$
$\mathbb {P}^3$
- Part of:
-
- Published online by Cambridge University Press:
- 18 September 2023, pp. 265-314
-
- Article
-
- You have access
- HTML
- Export citation
NON-ISOMORPHIC SMOOTH COMPACTIFICATIONS OF THE MODULI SPACE OF CUBIC SURFACES
- Part of:
-
- Published online by Cambridge University Press:
- 03 October 2023, pp. 315-365
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A BALL QUOTIENT PARAMETRIZING TRIGONAL GENUS 4 CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 21 September 2023, pp. 366-378
-
- Article
-
- You have access
- HTML
- Export citation
EXACT SUBCATEGORIES, SUBFUNCTORS OF
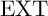 ${\operatorname{EXT}}$, AND SOME APPLICATIONS
${\operatorname{EXT}}$, AND SOME APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 27 September 2023, pp. 379-419
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A COMPARISON BETWEEN DWORK AND RIGID COHOMOLOGIES OF PROJECTIVE COMPLEMENTS
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2023, pp. 420-461
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCAL SECTIONS OF ARITHMETIC FUNDAMENTAL GROUPS OF p-ADIC CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2023, pp. 462-487
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
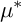 $\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
$\mu ^*$-ZARISKI PAIRS OF SURFACE SINGULARITIES
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2023, pp. 488-497
-
- Article
-
- You have access
- HTML
- Export citation
GENUS
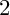 $2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
$2$ CURVES WITH BAD REDUCTION AT ONE ODD PRIME
- Part of:
-
- Published online by Cambridge University Press:
- 29 November 2023, pp. 498-512
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
NMJ volume 254 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 May 2024, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
NMJ volume 254 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation