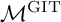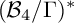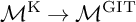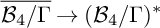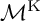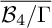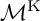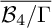1 Introduction
The four-dimensional moduli space
![]() $\mathcal {M}$
of smooth complex cubic surfaces is one of the gems of classical algebraic geometry. As a moduli space of hypersurfaces, it comes with a GIT model
$\mathcal {M}$
of smooth complex cubic surfaces is one of the gems of classical algebraic geometry. As a moduli space of hypersurfaces, it comes with a GIT model
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
, well-studied via the classical invariant theory (see [Reference DolgachevDol
Reference Alexeev3, Chap. 9], [Reference Dolgachev, van Geemen and KondoDvG]). Through an auxiliary construction with cubic threefolds, there is a Hodge-theoretic ball quotient model
${\mathcal {M}}^{\operatorname {GIT}}$
, well-studied via the classical invariant theory (see [Reference DolgachevDol
Reference Alexeev3, Chap. 9], [Reference Dolgachev, van Geemen and KondoDvG]). Through an auxiliary construction with cubic threefolds, there is a Hodge-theoretic ball quotient model
![]() ${\mathcal {B}_4/\Gamma }$
of the moduli space
${\mathcal {B}_4/\Gamma }$
of the moduli space
![]() $\mathcal {M}$
, and its Baily–Borel compactification
$\mathcal {M}$
, and its Baily–Borel compactification
![]() ${(\mathcal {B}_4/\Gamma )^*}$
[Reference Abramovich, Graber and VistoliACT] (see also [Reference du Plessis and WallDvG+] for an alternative construction of the ball quotient model, involving
${(\mathcal {B}_4/\Gamma )^*}$
[Reference Abramovich, Graber and VistoliACT] (see also [Reference du Plessis and WallDvG+] for an alternative construction of the ball quotient model, involving
![]() $K3$
surfaces instead, and [Reference Kudla and RapoportKR], [Reference ZhengZhe] for a construction via abelian varieties of Picard type, which also gives information on the field of definition of the period map). Finally, as cubic surfaces are Fano, there is a K-stable compactification [Reference OlssonOSS]. These three models of
$K3$
surfaces instead, and [Reference Kudla and RapoportKR], [Reference ZhengZhe] for a construction via abelian varieties of Picard type, which also gives information on the field of definition of the period map). Finally, as cubic surfaces are Fano, there is a K-stable compactification [Reference OlssonOSS]. These three models of
![]() $\mathcal {M}$
, each of a totally different nature, turn out to be isomorphic; in particular,
$\mathcal {M}$
, each of a totally different nature, turn out to be isomorphic; in particular,
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
by [Reference Abramovich, Graber and VistoliACT, Th. 3.17].
${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
by [Reference Abramovich, Graber and VistoliACT, Th. 3.17].
The moduli space
![]() $\mathcal {M}$
is open in
$\mathcal {M}$
is open in
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
, and the complement
${\mathcal {M}}^{\operatorname {GIT}}$
, and the complement
![]() ${\mathcal {M}}^{\operatorname {GIT}}-\mathcal {M}$
, which we refer to as the boundary or, equivalently, the discriminant, is an irreducible divisor. All of the points in the boundary, with the exception of one, parameterize cubic surfaces with
${\mathcal {M}}^{\operatorname {GIT}}-\mathcal {M}$
, which we refer to as the boundary or, equivalently, the discriminant, is an irreducible divisor. All of the points in the boundary, with the exception of one, parameterize cubic surfaces with
![]() $A_1$
singularities, which are GIT stable. The remaining point is the unique GIT boundary point
$A_1$
singularities, which are GIT stable. The remaining point is the unique GIT boundary point
![]() $\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
which, from the GIT (and also K-moduli) point of view, corresponds to the unique strictly polystable orbit of cubic surfaces with
$\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
which, from the GIT (and also K-moduli) point of view, corresponds to the unique strictly polystable orbit of cubic surfaces with
![]() $3A_2$
singularities. From the ball quotient perspective, under the identification
$3A_2$
singularities. From the ball quotient perspective, under the identification
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
,
${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
,
![]() $\Delta _{3A_2}$
is the unique cusp
$\Delta _{3A_2}$
is the unique cusp
![]() $c_{3A_2}$
of
$c_{3A_2}$
of
![]() ${(\mathcal {B}_4/\Gamma )^*}$
.
${(\mathcal {B}_4/\Gamma )^*}$
.
For the general GIT setup, in the case where one is taking a GIT quotient of a smooth projective variety, Kirwan has introduced a procedure, usually called the Kirwan blowup of the GIT moduli space, which we denote
![]() ${\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
in our case. The crucial point is that in general a Kirwan blowup is always a desingularization in the sense that it only has finite quotient singularities; alternatively, in the language of stacks, the natural quotient stack structure for the Kirwan blowup gives a smooth Deligne–Mumford stack. Similarly, to improve the singularities of the Baily–Borel compactification, one considers toroidal compactifications. Additionally, in some cases, one can attach modular meaning to some toroidal compactifications (e.g., [Reference Allcock, Carlson and ToledoAle2]). In general, a toroidal compactification depends on some choice of a fan, but for the case of ball quotients, the choice is unique, and we denote the toroidal compactification in our particular case by
${\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
in our case. The crucial point is that in general a Kirwan blowup is always a desingularization in the sense that it only has finite quotient singularities; alternatively, in the language of stacks, the natural quotient stack structure for the Kirwan blowup gives a smooth Deligne–Mumford stack. Similarly, to improve the singularities of the Baily–Borel compactification, one considers toroidal compactifications. Additionally, in some cases, one can attach modular meaning to some toroidal compactifications (e.g., [Reference Allcock, Carlson and ToledoAle2]). In general, a toroidal compactification depends on some choice of a fan, but for the case of ball quotients, the choice is unique, and we denote the toroidal compactification in our particular case by
![]() ${\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
. In our particular situation, it is a coincidence that
${\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
. In our particular situation, it is a coincidence that
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
has only finite quotient singularities. However, it still makes sense to consider the Kirwan blowup
${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
has only finite quotient singularities. However, it still makes sense to consider the Kirwan blowup
![]() ${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
, respectively, in the sense that they have a better chance of having modular interpretations (see, e.g., [Reference ZhangZha] for some related work) that would give rise to natural Deligne–Mumford moduli stacks.
${\overline {\mathcal {B}_4/\Gamma }}$
, respectively, in the sense that they have a better chance of having modular interpretations (see, e.g., [Reference ZhangZha] for some related work) that would give rise to natural Deligne–Mumford moduli stacks.
In our case, both
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are blowups of the same point
${\overline {\mathcal {B}_4/\Gamma }}$
are blowups of the same point
![]() $\Delta _{3A_2}(=c_{3A_2})$
on the same space
$\Delta _{3A_2}(=c_{3A_2})$
on the same space
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
. In [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1], we studied the cohomology of various compactifications for moduli of cubic threefolds and cubic surfaces. In particular, we showed that
${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
. In [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1], we studied the cohomology of various compactifications for moduli of cubic threefolds and cubic surfaces. In particular, we showed that
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
have the same cohomology, and we asked if
${\overline {\mathcal {B}_4/\Gamma }}$
have the same cohomology, and we asked if
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
were in fact isomorphic. This seems very plausible especially in the context of the recent work of Gallardo, Kerr, and Schaffler [Reference Gallardo, Kerr and SchafflerGKS] on the moduli of marked cubic surfaces. Namely, recall that the moduli space of cubic surfaces has a natural
${\overline {\mathcal {B}_4/\Gamma }}$
were in fact isomorphic. This seems very plausible especially in the context of the recent work of Gallardo, Kerr, and Schaffler [Reference Gallardo, Kerr and SchafflerGKS] on the moduli of marked cubic surfaces. Namely, recall that the moduli space of cubic surfaces has a natural
![]() $W(E_6)$
-cover
$W(E_6)$
-cover
![]() $\mathcal {M}_m$
obtained by labeling the
$\mathcal {M}_m$
obtained by labeling the
![]() $27$
lines on the cubic. Naruki [Reference NarukiN] proved that this marked moduli space
$27$
lines on the cubic. Naruki [Reference NarukiN] proved that this marked moduli space
![]() $\mathcal {M}_m$
admits a smooth normal crossing compactification
$\mathcal {M}_m$
admits a smooth normal crossing compactification
![]() $\overline {\mathcal {N}}$
(see also [Reference Hacking, Keel and TevelevHKT] for further modular interpretations attached to
$\overline {\mathcal {N}}$
(see also [Reference Hacking, Keel and TevelevHKT] for further modular interpretations attached to
![]() $\overline {\mathcal {N}}$
). On the other hand, Allcock, Carlson, and Toledo [Reference Abramovich, Graber and VistoliACT] noticed that the ball quotient model
$\overline {\mathcal {N}}$
). On the other hand, Allcock, Carlson, and Toledo [Reference Abramovich, Graber and VistoliACT] noticed that the ball quotient model
![]() ${(\mathcal {B}_4/\Gamma )^*}$
comes with a natural marked cover
${(\mathcal {B}_4/\Gamma )^*}$
comes with a natural marked cover
![]() ${(\mathcal {B}_4/\Gamma _m)^*}$
(with
${(\mathcal {B}_4/\Gamma _m)^*}$
(with
![]() $\Gamma _m\unlhd \Gamma $
and
$\Gamma _m\unlhd \Gamma $
and
![]() $\Gamma /\Gamma _m\cong W(E_6) \times \{ \pm 1 \}$
) and that the associated toroidal compactification
$\Gamma /\Gamma _m\cong W(E_6) \times \{ \pm 1 \}$
) and that the associated toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
behaves similarly to
${\overline {\mathcal {B}_4/\Gamma _m}}$
behaves similarly to
![]() $\overline {\mathcal {N}}$
. This was further clarified by Gallardo, Kerr, and Schaffler [Reference Gallardo, Kerr and SchafflerGKS] (see also Remark 4.7 for a quick alternative proof), who showed that in fact the Naruki and the marked toroidal compactifications agree:
$\overline {\mathcal {N}}$
. This was further clarified by Gallardo, Kerr, and Schaffler [Reference Gallardo, Kerr and SchafflerGKS] (see also Remark 4.7 for a quick alternative proof), who showed that in fact the Naruki and the marked toroidal compactifications agree:
![]() $\overline {\mathcal {N}}\cong {\overline {\mathcal {B}_4/\Gamma _m}}$
. Returning to the unmarked case, the main result of our paper is that, surprisingly,
$\overline {\mathcal {N}}\cong {\overline {\mathcal {B}_4/\Gamma _m}}$
. Returning to the unmarked case, the main result of our paper is that, surprisingly,
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are not isomorphic. Furthermore, we investigate and explain the geometry underlying this phenomenon.
${\overline {\mathcal {B}_4/\Gamma }}$
are not isomorphic. Furthermore, we investigate and explain the geometry underlying this phenomenon.
Theorem 1.1. Neither the birational map
![]() $f:{\mathcal {M}}^{\operatorname {K}}\dashrightarrow {\overline {\mathcal {B}_4/\Gamma }}$
from the Kirwan blowup of the GIT moduli space of cubic surfaces to the toroidal compactification of the ball quotient model, which is the identity on the moduli space
$f:{\mathcal {M}}^{\operatorname {K}}\dashrightarrow {\overline {\mathcal {B}_4/\Gamma }}$
from the Kirwan blowup of the GIT moduli space of cubic surfaces to the toroidal compactification of the ball quotient model, which is the identity on the moduli space
![]() $\mathcal {M}$
of smooth cubic surfaces, nor its inverse
$\mathcal {M}$
of smooth cubic surfaces, nor its inverse
![]() $f^{-1}$
, extends to a morphism of the compactifications.
$f^{-1}$
, extends to a morphism of the compactifications.
We provide a quick proof of this theorem by showing that the strict transform in
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
of the discriminant divisor (the closure of the locus of cubics with an
${\overline {\mathcal {B}_4/\Gamma }}$
of the discriminant divisor (the closure of the locus of cubics with an
![]() $A_1$
singularity) in
$A_1$
singularity) in
![]() ${(\mathcal {B}_4/\Gamma )^*}={\mathcal {M}}^{\operatorname {GIT}}$
meets the exceptional divisor in
${(\mathcal {B}_4/\Gamma )^*}={\mathcal {M}}^{\operatorname {GIT}}$
meets the exceptional divisor in
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
generically transversally, whereas this is not the case in
${\overline {\mathcal {B}_4/\Gamma }}$
generically transversally, whereas this is not the case in
![]() ${\mathcal {M}}^{\operatorname {K}}$
. This shows a priori that the period map f does not extend to an isomorphism. Using straightforward arguments from higher-dimensional birational geometry, using that both
${\mathcal {M}}^{\operatorname {K}}$
. This shows a priori that the period map f does not extend to an isomorphism. Using straightforward arguments from higher-dimensional birational geometry, using that both
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are
${\overline {\mathcal {B}_4/\Gamma }}$
are
![]() $\mathbb {Q}$
-factorial, one can deduce from this that neither the period map f, nor its inverse
$\mathbb {Q}$
-factorial, one can deduce from this that neither the period map f, nor its inverse
![]() $f^{-1}$
, extends to a morphism.
$f^{-1}$
, extends to a morphism.
While Theorem 1.1 shows that the Kirwan and toroidal compactifications are not naturally isomorphic, one could still wonder if the agreement of the Betti numbers, observed in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1], could be explained by an abstract isomorphism as complex projective varieties. To this end, we strengthen Theorem 1.1 by showing that
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are not abstractly isomorphic, and in fact not even K-equivalent.
${\overline {\mathcal {B}_4/\Gamma }}$
are not abstractly isomorphic, and in fact not even K-equivalent.
Recall that two birational normal projective
![]() $\mathbb {Q}$
-Gorenstein varieties X and Y are said to be K-equivalent if there exists a smooth variety Z dominating birationally both of them
$\mathbb {Q}$
-Gorenstein varieties X and Y are said to be K-equivalent if there exists a smooth variety Z dominating birationally both of them

such that
![]() $g^*K_X \sim _{\mathbb {Q}} h^*K_Y$
. Two facts about K-equivalent varieties that motivate our interest in this question are the following. First, it is known that smooth K-equivalent varieties have the same Betti numbers [Reference BatyrevB, Th. 1.1] (see, e.g., [Reference PopaP, Chap. 4, Th. 3.1] for the case where X and Y are not assumed to be Calabi–Yau). Second, birational normal projective
$g^*K_X \sim _{\mathbb {Q}} h^*K_Y$
. Two facts about K-equivalent varieties that motivate our interest in this question are the following. First, it is known that smooth K-equivalent varieties have the same Betti numbers [Reference BatyrevB, Th. 1.1] (see, e.g., [Reference PopaP, Chap. 4, Th. 3.1] for the case where X and Y are not assumed to be Calabi–Yau). Second, birational normal projective
![]() $\mathbb {Q}$
-Gorenstein varieties with canonical singularities, such that their canonical bundles are nef, are known to be K-equivalent (see [Reference KawamataKa, Lem. 4.4]). We are, however, in neither of these situations: first, the Kirwan and toroidal compactifications are singular (with finite quotient singularities), and second, the canonical bundles of the compactifications are far from being nef, as the spaces are birational to the
$\mathbb {Q}$
-Gorenstein varieties with canonical singularities, such that their canonical bundles are nef, are known to be K-equivalent (see [Reference KawamataKa, Lem. 4.4]). We are, however, in neither of these situations: first, the Kirwan and toroidal compactifications are singular (with finite quotient singularities), and second, the canonical bundles of the compactifications are far from being nef, as the spaces are birational to the
![]() $\mathbb {Q}$
-Fano variety
$\mathbb {Q}$
-Fano variety
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
. As it turns out, these two compactifications are not K-equivalent.
${\mathcal {M}}^{\operatorname {GIT}}$
. As it turns out, these two compactifications are not K-equivalent.
Theorem 1.2. The Kirwan compactification
![]() ${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
of the moduli space of smooth cubic surfaces
${\overline {\mathcal {B}_4/\Gamma }}$
of the moduli space of smooth cubic surfaces
![]() $\mathcal {M}$
are not K-equivalent.
$\mathcal {M}$
are not K-equivalent.
We prove Theorem 1.2 by showing that the top self-intersection numbers of the canonical bundles of the two compactifications are different. Clearly, Theorem 1.2 implies Theorem 1.1 (since it implies that f does not extend to an isomorphism). However, we prefer first to give an independent proof of Theorem 1.1 in §4, as this also helps elucidate the geometry of the compactifications. This approach can also be used in other contexts such as cubic threefolds or other Deligne–Mostow spaces. A further major ingredient of our proof is an explicit geometric recipe for computing the canonical class of a Kirwan blowup of a GIT quotient. This works in full generality, so long as the strictly semi-stable locus has codimension at least
![]() $2$
, which we explain in §6, and which may be of independent interest (see also Remark 6.6 regarding the singularities of these spaces).
$2$
, which we explain in §6, and which may be of independent interest (see also Remark 6.6 regarding the singularities of these spaces).
In the absence of odd cohomology (as is the case here), another possible explanation for the equality of Betti numbers of
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${(\mathcal {B}_4/\Gamma )^*}$
could be their
${(\mathcal {B}_4/\Gamma )^*}$
could be their
![]() $\mathbb {L}$
-equivalence in the Grothendieck ring of varieties. We prove that in fact the classes of these compactifications are equal in the Grothendieck ring of varieties.
$\mathbb {L}$
-equivalence in the Grothendieck ring of varieties. We prove that in fact the classes of these compactifications are equal in the Grothendieck ring of varieties.
Theorem 1.3. The Kirwan compactification
![]() ${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
of the moduli space of smooth cubic surfaces
${\overline {\mathcal {B}_4/\Gamma }}$
of the moduli space of smooth cubic surfaces
![]() $\mathcal {M}$
are equivalent in the Grothendieck ring of varieties.
$\mathcal {M}$
are equivalent in the Grothendieck ring of varieties.
The structure of the paper is as follows. We start in §2 by discussing a simple explicit example, for motivation. This example is of two birational surfaces, which are equivalent in the Grothendieck ring, but not K-equivalent. These are obtained as different blowups of
![]() $\mathbb {P}^2$
supported at one point. While this is not a GIT problem, the example demonstrates some of the features similar to our case of the moduli of cubic surfaces, and serves as motivation. In §3, we recall the constructions and the geometry of the compactifications of the moduli space of cubic surfaces, and give the formulas for the discriminant and boundary divisors in local coordinates, as well as the crucial computation of the finite stabilizers of points on them. Some of the proofs are by detailed explicit computations, which are given in the Appendix. In particular, in §3, we obtain the resulting non-transversality results for the Kirwan blowup needed for proving Theorem 1.1. In §4, we discuss the geometry of the ball quotient model in detail, obtain the resulting transversality results for the toroidal compactification, and thereby give a direct proof of Theorem 1.1. In §5, we provide details on the canonical bundles of the ball quotient models.
$\mathbb {P}^2$
supported at one point. While this is not a GIT problem, the example demonstrates some of the features similar to our case of the moduli of cubic surfaces, and serves as motivation. In §3, we recall the constructions and the geometry of the compactifications of the moduli space of cubic surfaces, and give the formulas for the discriminant and boundary divisors in local coordinates, as well as the crucial computation of the finite stabilizers of points on them. Some of the proofs are by detailed explicit computations, which are given in the Appendix. In particular, in §3, we obtain the resulting non-transversality results for the Kirwan blowup needed for proving Theorem 1.1. In §4, we discuss the geometry of the ball quotient model in detail, obtain the resulting transversality results for the toroidal compactification, and thereby give a direct proof of Theorem 1.1. In §5, we provide details on the canonical bundles of the ball quotient models.
Going further, in §6, we develop the general machinery for relating the canonical bundle of a GIT compactification and its Kirwan desingularization. We then specialize to our case, and compute the canonical bundle of
![]() ${\mathcal {M}}^{\operatorname {K}}$
. Finally, we prove our main results in §7, where we establish the non-K-equivalence of the Kirwan blowup
${\mathcal {M}}^{\operatorname {K}}$
. Finally, we prove our main results in §7, where we establish the non-K-equivalence of the Kirwan blowup
![]() ${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
, and in §8, where we show their equivalence in the Grothendieck ring. The first requires a discussion of the top self-intersection numbers of canonical bundles on these varieties, and the second relies on a concrete description of the boundary of the Kirwan blowup as a quotient of a toric variety by a finite group. In the Appendix, we collect a number of results whose proofs are based on explicit computations in the Luna slice.
${\overline {\mathcal {B}_4/\Gamma }}$
, and in §8, where we show their equivalence in the Grothendieck ring. The first requires a discussion of the top self-intersection numbers of canonical bundles on these varieties, and the second relies on a concrete description of the boundary of the Kirwan blowup as a quotient of a toric variety by a finite group. In the Appendix, we collect a number of results whose proofs are based on explicit computations in the Luna slice.
Remark 1.4. One of our motivations for this paper is our systematic investigation of the moduli space of cubic threefolds and its compactifications (e.g., [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1] and the references within). In that case as well, there are a toroidal compactification of a ball quotient model and a Kirwan blowup of the natural GIT quotient. Furthermore, as here, the two models have the same cohomology. Methods similar to those used in the proof of Theorem 1.1 show that for moduli of cubic threefolds, the natural period map does not extend to an isomorphism, either. However, the more refined results (Theorems 1.2 and 1.3) seem at the moment out of reach for cubic threefolds.
We also note that there are other related moduli spaces where these techniques apply, such as the moduli space of cubic surfaces with a line (see Remark 4.3). Again, we will not pursue this here.
2 A motivating example
Before discussing the case of the moduli of cubic surfaces, we present an elementary example that captures some of the essential aspects of our arguments. While we are not aware of a global moduli interpretation of the example discussed here, the motivation and the construction of the example comes from the local study of semi-stable reduction for curves with an
![]() $A_2$
singularity (see esp. [Reference Coskun and Prendergast-SmithCML+2]), and it is at least morally related to the moduli of cubic surfaces discussed here (see, e.g., [Reference Casalaina-Martin and LazaCMG+2, §1]).
$A_2$
singularity (see esp. [Reference Coskun and Prendergast-SmithCML+2]), and it is at least morally related to the moduli of cubic surfaces discussed here (see, e.g., [Reference Casalaina-Martin and LazaCMG+2, §1]).
Namely, consider the pair
![]() $(M,D)$
consisting of
$(M,D)$
consisting of
![]() $M\cong \mathbb {P}^2$
together with a cuspidal cubic D. Let
$M\cong \mathbb {P}^2$
together with a cuspidal cubic D. Let
![]() $o\in D$
be the cusp point. Define
$o\in D$
be the cusp point. Define
![]() $M'$
to be the (standard) blowup of
$M'$
to be the (standard) blowup of
![]() $M\cong \mathbb {P}^2$
at o, with the exceptional divisor
$M\cong \mathbb {P}^2$
at o, with the exceptional divisor
![]() $E'\subseteq M'$
, and let
$E'\subseteq M'$
, and let
![]() $\widehat M$
be the standard log resolution of the cusp, obtained by two further blowups of
$\widehat M$
be the standard log resolution of the cusp, obtained by two further blowups of
![]() $M'$
, with exceptional divisors
$M'$
, with exceptional divisors
![]() $E_1,E_2,E_3$
over M. We label the exceptional divisors on
$E_1,E_2,E_3$
over M. We label the exceptional divisors on
![]() $\widehat M$
in such a way that
$\widehat M$
in such a way that
![]() $(E_i)^2=i-4$
; that is,
$(E_i)^2=i-4$
; that is,
![]() $E_1$
is the strict transform of
$E_1$
is the strict transform of
![]() $E'$
. We contract
$E'$
. We contract
![]() $E_1$
and
$E_1$
and
![]() $E_2$
on
$E_2$
on
![]() $\widehat M$
and obtain
$\widehat M$
and obtain
![]() $\overline M$
, which will have two quotient singularities of types
$\overline M$
, which will have two quotient singularities of types
![]() $\frac {1}{2}(1,1)$
(or equivalently
$\frac {1}{2}(1,1)$
(or equivalently
![]() $A_1$
) and
$A_1$
) and
![]() $\frac {1}{3}(1,1)$
(e.g., simply note that
$\frac {1}{3}(1,1)$
(e.g., simply note that
![]() $E_1^2=-3$
,
$E_1^2=-3$
,
![]() $E_2^2=-2$
, and that
$E_2^2=-2$
, and that
![]() $E_1$
and
$E_1$
and
![]() $E_2$
do not intersect) and we denote by
$E_2$
do not intersect) and we denote by
![]() $\overline E\subseteq \overline M$
the exceptional divisor of the blowdown
$\overline E\subseteq \overline M$
the exceptional divisor of the blowdown
![]() $\overline M\to M$
, so that
$\overline M\to M$
, so that
![]() $\overline E$
is the image of
$\overline E$
is the image of
![]() $E_3\subseteq \widehat M$
. We obtain the following diagram:
$E_3\subseteq \widehat M$
. We obtain the following diagram:

Clearly,
![]() $\overline M$
is a blowup of M at o, and in fact it is a single weighted blowup of M at o. In conclusion, both
$\overline M$
is a blowup of M at o, and in fact it is a single weighted blowup of M at o. In conclusion, both
![]() $M'$
and
$M'$
and
![]() $\overline M$
are blowups of M at o. Both are
$\overline M$
are blowups of M at o. Both are
![]() $\mathbb {Q}$
-factorial with klt singularities, but they are non-isomorphic (e.g.,
$\mathbb {Q}$
-factorial with klt singularities, but they are non-isomorphic (e.g.,
![]() $M'$
is smooth, whereas
$M'$
is smooth, whereas
![]() $\overline M$
is singular). More in line with our arguments, we note that the birational map
$\overline M$
is singular). More in line with our arguments, we note that the birational map
![]() $f:M'\dashrightarrow \overline M$
does not extend to an isomorphism, since the exceptional divisors
$f:M'\dashrightarrow \overline M$
does not extend to an isomorphism, since the exceptional divisors
![]() $E'\subseteq M'$
and
$E'\subseteq M'$
and
![]() $\overline E\subseteq \overline M$
and the strict transforms of D (denote them
$\overline E\subseteq \overline M$
and the strict transforms of D (denote them
![]() $D'\subseteq M'$
and
$D'\subseteq M'$
and
![]() $\overline D\subseteq \overline M$
) are non-transversal in
$\overline D\subseteq \overline M$
) are non-transversal in
![]() $M'$
, but are transversal in
$M'$
, but are transversal in
![]() $\overline M$
. In fact, note that
$\overline M$
. In fact, note that
![]() $(\overline M, \overline D+\overline E)$
is dlt, whereas
$(\overline M, \overline D+\overline E)$
is dlt, whereas
![]() $(M', D'+E')$
is not. This shows that even though
$(M', D'+E')$
is not. This shows that even though
![]() $\overline M$
is singular, when accounting for the discriminant D, the correct resolution of M is in fact
$\overline M$
is singular, when accounting for the discriminant D, the correct resolution of M is in fact
![]() $\overline M$
and not
$\overline M$
and not
![]() $M'$
(which is smooth!). Clearly,
$M'$
(which is smooth!). Clearly,
![]() $M'$
and
$M'$
and
![]() $\overline M$
have the same Betti numbers, and are equal in the Grothendieck ring of varieties. On the other hand, an elementary computation shows that
$\overline M$
have the same Betti numbers, and are equal in the Grothendieck ring of varieties. On the other hand, an elementary computation shows that
![]() $M'$
and
$M'$
and
![]() $\overline M$
are not K-equivalent. Namely,
$\overline M$
are not K-equivalent. Namely,
![]() $K_{M'}^2=8$
(as
$K_{M'}^2=8$
(as
![]() $M'$
is a single regular blowup of
$M'$
is a single regular blowup of
![]() $\mathbb {P}^2$
), whereas
$\mathbb {P}^2$
), whereas
![]() $K_{\overline M}^2=6+\frac {1}{3}$
, since
$K_{\overline M}^2=6+\frac {1}{3}$
, since
![]() $K_{\widehat M}=\bar \pi ^*K_{\overline M}-\frac {1}{3} E_1$
(as the discrepancy of a quotient singularity of type
$K_{\widehat M}=\bar \pi ^*K_{\overline M}-\frac {1}{3} E_1$
(as the discrepancy of a quotient singularity of type
![]() $\frac {1}{n}(1,1)$
is
$\frac {1}{n}(1,1)$
is
![]() $\frac {2-n}{n}$
).
$\frac {2-n}{n}$
).
We note that the weighted blowup
![]() $\overline M\to M$
is motivated by [Reference Coskun and Prendergast-SmithCML+2], which discusses the simultaneous semi-stable reduction for curves with certain singularities. Indeed, locally near the cusp o, the pair
$\overline M\to M$
is motivated by [Reference Coskun and Prendergast-SmithCML+2], which discusses the simultaneous semi-stable reduction for curves with certain singularities. Indeed, locally near the cusp o, the pair
![]() $(M,D)$
can be identified with the versal deformation for
$(M,D)$
can be identified with the versal deformation for
![]() $A_2$
singularities, with D being the discriminant. From this perspective, it is natural to consider (locally near o) the
$A_2$
singularities, with D being the discriminant. From this perspective, it is natural to consider (locally near o) the
![]() $W(A_2)$
cover
$W(A_2)$
cover
![]() $\widetilde M$
of M branched over D. On this cover, the discriminant D pulls back to the
$\widetilde M$
of M branched over D. On this cover, the discriminant D pulls back to the
![]() $A_2$
hyperplane arrangement. The standard blowup
$A_2$
hyperplane arrangement. The standard blowup
![]() $\widehat {\widetilde M}$
at
$\widehat {\widetilde M}$
at
![]() $\widetilde o\in \widetilde M$
(the preimage of o) leads to a normal crossing discriminant (see [Reference Coskun and Prendergast-SmithCML+2] for the general construction and discussion). Clearly,
$\widetilde o\in \widetilde M$
(the preimage of o) leads to a normal crossing discriminant (see [Reference Coskun and Prendergast-SmithCML+2] for the general construction and discussion). Clearly,
![]() $W(A_2)$
acts on
$W(A_2)$
acts on
![]() $\widehat {\widetilde M}$
, and
$\widehat {\widetilde M}$
, and
![]() $\overline M$
can be recovered as the quotient
$\overline M$
can be recovered as the quotient
![]() $\widehat {\widetilde M}/W(A_2)$
(again, the discussion is meant locally near o). The main point of this construction is that it takes into account the monodromy around the discriminant divisor, and thus it leads to a modular resolution
$\widehat {\widetilde M}/W(A_2)$
(again, the discussion is meant locally near o). The main point of this construction is that it takes into account the monodromy around the discriminant divisor, and thus it leads to a modular resolution
![]() $\overline M$
of the pair
$\overline M$
of the pair
![]() $(M,D)$
(see [Reference Coskun and Prendergast-SmithCML+2] for precise statements).
$(M,D)$
(see [Reference Coskun and Prendergast-SmithCML+2] for precise statements).
Similarly, returning to our setup in the current paper, the toroidal compactification of the moduli space of cubic surfaces is a modular blowup of the Baily–Borel compactification, which takes into account the monodromy around the discriminant divisor. In contrast, the Kirwan resolution of the GIT quotient does not see the monodromy, and consequently the Kirwan blowup behaves more like the standard blowup
![]() $M'\to M$
. What we see is that while the GIT compactification and the Baily–Borel compactification for the moduli of cubic surfaces are isomorphic as projective varieties, the natural stack structure (even at certain stable points) is different. Namely, at the generic point of the discriminant divisor, corresponding to a cubic with an
$M'\to M$
. What we see is that while the GIT compactification and the Baily–Borel compactification for the moduli of cubic surfaces are isomorphic as projective varieties, the natural stack structure (even at certain stable points) is different. Namely, at the generic point of the discriminant divisor, corresponding to a cubic with an
![]() $A_1$
singularity, on the GIT side, there are no extra automorphisms (i.e., the stabilizer of the generic point of the discriminant is the diagonal
$A_1$
singularity, on the GIT side, there are no extra automorphisms (i.e., the stabilizer of the generic point of the discriminant is the diagonal
![]() $\mu _4$
in
$\mu _4$
in
![]() $\operatorname {SL}(4,\mathbb {C})$
, which induces the trivial automorphism of the cubic surface), whereas on the Hodge theoretic side, there is an extra automorphism given by the Picard–Lefschetz transformation corresponding to the nodal degenerations (cf. [Reference Odaka, Spotti and SunO, p. 125]).
$\operatorname {SL}(4,\mathbb {C})$
, which induces the trivial automorphism of the cubic surface), whereas on the Hodge theoretic side, there is an extra automorphism given by the Picard–Lefschetz transformation corresponding to the nodal degenerations (cf. [Reference Odaka, Spotti and SunO, p. 125]).
3 The GIT models for the moduli of cubic surfaces
As is the case in general for hypersurfaces, the moduli of cubic surfaces has a natural compact model: the GIT compactification
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
. For cubic surfaces,
${\mathcal {M}}^{\operatorname {GIT}}$
. For cubic surfaces,
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
is well understood via classical invariant theory; in particular,
${\mathcal {M}}^{\operatorname {GIT}}$
is well understood via classical invariant theory; in particular,
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
. Here, we are interested in the Kirwan blowup
${\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
. Here, we are interested in the Kirwan blowup
![]() ${\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
, which is obtained by blowing up the unique GIT strictly polystable boundary point
${\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
, which is obtained by blowing up the unique GIT strictly polystable boundary point
![]() $\Delta \in {\mathcal {M}}^{\operatorname {GIT}}$
according to a general procedure due to Kirwan [Reference KirwanKi1]. After reviewing
$\Delta \in {\mathcal {M}}^{\operatorname {GIT}}$
according to a general procedure due to Kirwan [Reference KirwanKi1]. After reviewing
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
and
${\mathcal {M}}^{\operatorname {GIT}}$
and
![]() ${\mathcal {M}}^{\operatorname {K}}$
, we discuss the local structure of the Kirwan blowup
${\mathcal {M}}^{\operatorname {K}}$
, we discuss the local structure of the Kirwan blowup
![]() ${\mathcal {M}}^{\operatorname {K}}$
along the exceptional divisor
${\mathcal {M}}^{\operatorname {K}}$
along the exceptional divisor
![]() $D_{3A_2}$
. We conclude in Proposition 3.9 that the exceptional divisor
$D_{3A_2}$
. We conclude in Proposition 3.9 that the exceptional divisor
![]() $D_{3A_2}$
and the strict transform
$D_{3A_2}$
and the strict transform
![]() $\widetilde D_{A_1}$
of the discriminant divisor do not meet, even generically, transversally in
$\widetilde D_{A_1}$
of the discriminant divisor do not meet, even generically, transversally in
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
.
${\mathcal {M}}^{\operatorname {GIT}}$
.
3.1 Preliminaries on moduli of cubic surfaces
We denote by
the four-dimensional moduli space of smooth (complex) cubic surfaces, where
![]() $\mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))^\circ $
denotes the locus of smooth cubic surfaces embedded in
$\mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))^\circ $
denotes the locus of smooth cubic surfaces embedded in
![]() $\mathbb {P}^3$
. We denote by
$\mathbb {P}^3$
. We denote by
the GIT compactification, and by
the Kirwan resolution of
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
. The GIT stability for cubic surfaces has been completely described (see, e.g., [Reference MumfordMuk, §7.2(b)]). For a cubic surface
${\mathcal {M}}^{\operatorname {GIT}}$
. The GIT stability for cubic surfaces has been completely described (see, e.g., [Reference MumfordMuk, §7.2(b)]). For a cubic surface
![]() $S\subseteq \mathbb {P}^3$
:
$S\subseteq \mathbb {P}^3$
:
-
• S is stable if and only if it has at worst
 $A_1$
singularities,
$A_1$
singularities, -
• S is semi-stable if and only if it is stable, or has at worst
 $A_2$
singularities, and does not contain the axes of the
$A_2$
singularities, and does not contain the axes of the
 $A_2$
singularities,
$A_2$
singularities, -
• S is strictly polystable if and only if it is projectively equivalent to the so-called
 $3A_2$
cubic surface which has exactly three singular points, each of which is an
$3A_2$
cubic surface which has exactly three singular points, each of which is an
 $A_2$
singularity.
$A_2$
singularity.
It is a classical result (see [Reference du Plessis and WallDvG+, (2.4)]) that the GIT compactification
is a weighted projective space. We will denote by
the so-called discriminant divisor, that is, the closure of the locus of (stable) cubics with an
![]() $A_1$
singularity. This divisor is irreducible, as the locus of corresponding cubics in
$A_1$
singularity. This divisor is irreducible, as the locus of corresponding cubics in
![]() $\mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
is irreducible; the general point is given by the orbit of the locus of cubics of the form
$\mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
is irreducible; the general point is given by the orbit of the locus of cubics of the form
![]() $x_0q(x_1,x_2,x_3)+f(x_1,x_2,x_3)$
with
$x_0q(x_1,x_2,x_3)+f(x_1,x_2,x_3)$
with
![]() $q(x_1,x_2,x_3)$
a smooth quadric, and
$q(x_1,x_2,x_3)$
a smooth quadric, and
![]() $f(x_1,x_2,x_3)$
a cubic.
$f(x_1,x_2,x_3)$
a cubic.
We denote by
the so-called Eckardt divisor, which generically parameterizes smooth cubic surfaces having an Eckardt point—a point that lies on three lines contained in the cubic surface. This divisor is also irreducible, as the corresponding locus in
![]() $\mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
is irreducible; the locus of smooth Eckardt cubics is the orbit of the locus of cubics of the form
$\mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
is irreducible; the locus of smooth Eckardt cubics is the orbit of the locus of cubics of the form
![]() $x_0^2\ell (x_1,x_2,x_3)+f(x_1,x_2,x_3)$
with
$x_0^2\ell (x_1,x_2,x_3)+f(x_1,x_2,x_3)$
with
![]() $\ell (x_1,x_2,x_3)$
a linear form and
$\ell (x_1,x_2,x_3)$
a linear form and
![]() $f(x_1,x_2,x_3)$
a cubic, with the line and cubic meeting transversally. In the coordinates of the previous equation, the point
$f(x_1,x_2,x_3)$
a cubic, with the line and cubic meeting transversally. In the coordinates of the previous equation, the point
![]() $(1:0:0:0)$
is then an Eckardt point, and the three lines through the Eckardt point are the ones determined by the Eckardt point and the intersection
$(1:0:0:0)$
is then an Eckardt point, and the three lines through the Eckardt point are the ones determined by the Eckardt point and the intersection
![]() $\{\ell =f=0\}$
in the hyperplane at infinity. Such an Eckardt cubic in these coordinates has an involution given by
$\{\ell =f=0\}$
in the hyperplane at infinity. Such an Eckardt cubic in these coordinates has an involution given by
![]() $x_0\mapsto -x_0$
. Note that a general smooth cubic surface with an Eckardt point has a unique Eckardt point, and has automorphism group
$x_0\mapsto -x_0$
. Note that a general smooth cubic surface with an Eckardt point has a unique Eckardt point, and has automorphism group
![]() $\mathbb {Z}_2$
, and moreover, the Eckardt divisor R contains the locus of all smooth cubic surfaces that have any nontrivial automorphism (see, e.g., [Reference Dardanelli and van GeemenDD, Table 1 and Fig. 1]).
$\mathbb {Z}_2$
, and moreover, the Eckardt divisor R contains the locus of all smooth cubic surfaces that have any nontrivial automorphism (see, e.g., [Reference Dardanelli and van GeemenDD, Table 1 and Fig. 1]).
From the description of stability given above, it follows that
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
contains a unique strictly polystable point
${\mathcal {M}}^{\operatorname {GIT}}$
contains a unique strictly polystable point
![]() $\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
corresponding to the orbit of the
$\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
corresponding to the orbit of the
![]() $3A_2$
cubic
$3A_2$
cubic
![]() $S_{3A_2}$
, and consequently the Kirwan resolution
$S_{3A_2}$
, and consequently the Kirwan resolution
![]() ${\mathcal {M}}^{\operatorname {K}}$
of
${\mathcal {M}}^{\operatorname {K}}$
of
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
is a blowup with center supported at
${\mathcal {M}}^{\operatorname {GIT}}$
is a blowup with center supported at
![]() $\Delta _{3A_2}$
(see, e.g., [Reference KirwanKi2], [Reference ZhangZha]); we denote by
$\Delta _{3A_2}$
(see, e.g., [Reference KirwanKi2], [Reference ZhangZha]); we denote by
the exceptional divisor, which is irreducible (as is the case for exceptional divisors in Kirwan blowups, being the quotient of an open subset of the blowup of a smooth irreducible subvariety of a smooth irreducible variety). Note that
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() $D_{3A_2}$
are, by construction, smooth up to finite quotient singularities. We will denote by
$D_{3A_2}$
are, by construction, smooth up to finite quotient singularities. We will denote by
![]() $\widetilde {D}_{A_1}\subseteq {\mathcal {M}}^{\operatorname {K}}$
the strict transform of the discriminant divisor
$\widetilde {D}_{A_1}\subseteq {\mathcal {M}}^{\operatorname {K}}$
the strict transform of the discriminant divisor
![]() $D_{A_1}\subseteq {\mathcal {M}}^{\operatorname {GIT}}$
, and by
$D_{A_1}\subseteq {\mathcal {M}}^{\operatorname {GIT}}$
, and by
![]() $\widetilde {R}\subseteq {\mathcal {M}}^{\operatorname {K}}$
the strict transform of the Eckardt divisor
$\widetilde {R}\subseteq {\mathcal {M}}^{\operatorname {K}}$
the strict transform of the Eckardt divisor
![]() $R\subseteq {\mathcal {M}}^{\operatorname {GIT}}$
.
$R\subseteq {\mathcal {M}}^{\operatorname {GIT}}$
.
3.2 Geometry of
 ${\mathcal {M}}^{\operatorname {GIT}}$
as a weighted projective space
${\mathcal {M}}^{\operatorname {GIT}}$
as a weighted projective space
In full generality, consider a weighted projective space
![]() $\mathbb {P}(q_0,\dots , q_n)=\operatorname {Proj}\mathbb {C}[x_0,\dots ,x_n]=(\mathbb {C}^{n+1}-\{0\})/\mathbb {C}^*$
, where the weight of
$\mathbb {P}(q_0,\dots , q_n)=\operatorname {Proj}\mathbb {C}[x_0,\dots ,x_n]=(\mathbb {C}^{n+1}-\{0\})/\mathbb {C}^*$
, where the weight of
![]() $x_i$
(resp. the weight of the action of
$x_i$
(resp. the weight of the action of
![]() $\mathbb {C}^*$
on
$\mathbb {C}^*$
on
![]() $x_i$
) is
$x_i$
) is
![]() $q_i$
for
$q_i$
for
![]() $i=0,\dots ,n$
, where, without loss of generality, we assume that
$i=0,\dots ,n$
, where, without loss of generality, we assume that
![]() $\gcd (q_0,\dots , q_n)=1$
[Reference DolgachevDol
Reference Abramovich, Graber and Vistoli1, Prop. p. 37]. Denoting
$\gcd (q_0,\dots , q_n)=1$
[Reference DolgachevDol
Reference Abramovich, Graber and Vistoli1, Prop. p. 37]. Denoting
![]() , where
, where
![]() $\mu _{\ell }$
is the multiplicative group of roots of unity of order
$\mu _{\ell }$
is the multiplicative group of roots of unity of order
![]() $\ell $
, and letting the group
$\ell $
, and letting the group
![]() $G_{\vec q}$
act diagonally on
$G_{\vec q}$
act diagonally on
![]() $\mathbb {P}^n$
, we can express the weighted projective space as the quotient
$\mathbb {P}^n$
, we can express the weighted projective space as the quotient
with quotient map
This is the map of spaces associated with the identification of the graded ring
![]() $\mathbb {C}[x_0,\dots ,x_n]$
as the subring
$\mathbb {C}[x_0,\dots ,x_n]$
as the subring
![]() $\mathbb {C}[y_0^{q_1},\dots ,y_n^{q_n}]\subseteq \mathbb {C}[y_0,\dots ,y_n]$
of the standard graded polynomial ring, which can be viewed as the invariant ring for the group
$\mathbb {C}[y_0^{q_1},\dots ,y_n^{q_n}]\subseteq \mathbb {C}[y_0,\dots ,y_n]$
of the standard graded polynomial ring, which can be viewed as the invariant ring for the group
![]() $G_{\vec q}$
acting diagonally.
$G_{\vec q}$
acting diagonally.
While
![]() $G_{\vec q}$
need not be cyclic, the weighted projective space is locally a cyclic quotient. It is covered by the open sets
$G_{\vec q}$
need not be cyclic, the weighted projective space is locally a cyclic quotient. It is covered by the open sets
![]() (i.e.,
(i.e.,
![]() $U_i$
is the image of
$U_i$
is the image of
![]() $\{x_i \neq 0\}\subseteq \mathbb {C}^{n+1}-\{0\}$
under the quotient map h), and one has
$\{x_i \neq 0\}\subseteq \mathbb {C}^{n+1}-\{0\}$
under the quotient map h), and one has
where
![]() $\zeta _{q_i}$
is a primitive root of unity of order
$\zeta _{q_i}$
is a primitive root of unity of order
![]() $q_i$
. This identification comes from the identification
$q_i$
. This identification comes from the identification
![]() $U_i=\operatorname {Spec}(\mathbb {C}[x_0,\dots ,x_n]_{(x_i)})$
, where
$U_i=\operatorname {Spec}(\mathbb {C}[x_0,\dots ,x_n]_{(x_i)})$
, where
![]() $\mathbb {C}[x_0,\dots ,x_n]_{(x_i)}$
is the subring of elements of degree
$\mathbb {C}[x_0,\dots ,x_n]_{(x_i)}$
is the subring of elements of degree
![]() $0$
in the localized ring
$0$
in the localized ring
![]() $\mathbb {C}[x_0,\dots ,x_n]_{x_i}$
, and the identification of the ring
$\mathbb {C}[x_0,\dots ,x_n]_{x_i}$
, and the identification of the ring
![]() $\mathbb {C}[x_0,\dots ,x_n]_{(x_i)}$
with the subring of
$\mathbb {C}[x_0,\dots ,x_n]_{(x_i)}$
with the subring of
![]() $\mathbb {C}[z_0,\dots ,z_{i-1},z_{i+1},\dots ,z_n]^{\mu _{q_i}} \subseteq \mathbb {C}[z_0,\dots ,z_{i-1},z_{i+1},\dots ,z_n]$
of invariants for the diagonal action of the cyclic group
$\mathbb {C}[z_0,\dots ,z_{i-1},z_{i+1},\dots ,z_n]^{\mu _{q_i}} \subseteq \mathbb {C}[z_0,\dots ,z_{i-1},z_{i+1},\dots ,z_n]$
of invariants for the diagonal action of the cyclic group
![]() $\mu _{q_i}=\langle (\zeta _{q_i}^{q_0}, \dots ,\zeta _{q_i}^{q_{i-1}}, \zeta _{q_i}^{q_{i+1}}, \dots ,\zeta _{q_i}^{q_{n}}) \rangle $
.
$\mu _{q_i}=\langle (\zeta _{q_i}^{q_0}, \dots ,\zeta _{q_i}^{q_{i-1}}, \zeta _{q_i}^{q_{i+1}}, \dots ,\zeta _{q_i}^{q_{n}}) \rangle $
.
It is now straightforward to apply the Reid–Shepherd-Barron–Tai (RSBT) criterion to
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
, by local computations in these charts.
${\mathcal {M}}^{\operatorname {GIT}}$
, by local computations in these charts.
Lemma 3.1. The space
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
has canonical singularities.
${\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
has canonical singularities.
Proof. We first note that
![]() $U_0 \cong \mathbb {C}^4$
. To explain the other charts, we first treat the chart
$U_0 \cong \mathbb {C}^4$
. To explain the other charts, we first treat the chart
where
There is only one fixed point of this finite group action, namely the origin. Here, the RSBT criterion tells us that we have to check for all nontrivial powers
![]() $g_4^k$
that the inequality
$g_4^k$
that the inequality
holds. Altogether we find one singularity in this chart, namely the point
![]() $P_4=(0:0:0:0:1)$
, that is, the image of the point
$P_4=(0:0:0:0:1)$
, that is, the image of the point
![]() $(0,0,0,0,1)\in \mathbb {C}^{n+1}-\{0\}$
under the quotient map h. The singularity at this point is canonical. The other open sets
$(0,0,0,0,1)\in \mathbb {C}^{n+1}-\{0\}$
under the quotient map h. The singularity at this point is canonical. The other open sets
![]() $U_i$
can be treated similarly. The situation for
$U_i$
can be treated similarly. The situation for
![]() $U_2$
is completely analogous, and we find one further canonical singularity, namely
$U_2$
is completely analogous, and we find one further canonical singularity, namely
![]() $P_2=(0:0:1:0:0)$
. For
$P_2=(0:0:1:0:0)$
. For
![]() $U_3$
, we have to consider
$U_3$
, we have to consider
Once again, we find one canonical singular point, namely
![]() $P_3=(0:0:0:1:0)$
. Finally, in the chart
$P_3=(0:0:0:1:0)$
. Finally, in the chart
we have a one-dimensional fixed locus, namely the line
We also note that
![]() $g_4^2=g_2$
and that
$g_4^2=g_2$
and that
![]() $P_3 \in L$
. Outside
$P_3 \in L$
. Outside
![]() $P_3$
, we have a transversal singularity along L of type
$P_3$
, we have a transversal singularity along L of type
![]() $\mathbb {C}^3/\langle (-1,-1,-1) \rangle $
.
$\mathbb {C}^3/\langle (-1,-1,-1) \rangle $
.
In the proof of the lemma, we have also verified that
as already stated in [Reference du Plessis and WallDvG+, §6.9].
We note that the space
![]() ${\mathcal {M}}^{\operatorname {GIT}}=\mathbb {P}(1,2,3,4,5)$
is
${\mathcal {M}}^{\operatorname {GIT}}=\mathbb {P}(1,2,3,4,5)$
is
![]() $\mathbb {Q}$
-factorial (since it only has finite quotient singularities), and is thus
$\mathbb {Q}$
-factorial (since it only has finite quotient singularities), and is thus
![]() $\mathbb {Q}$
-Gorenstein, but it is not Gorenstein. Indeed, the line bundle
$\mathbb {Q}$
-Gorenstein, but it is not Gorenstein. Indeed, the line bundle
![]() $\mathcal {O}_{\mathbb {P}^n}(1)$
descends under the cover h (3.3) to a
$\mathcal {O}_{\mathbb {P}^n}(1)$
descends under the cover h (3.3) to a
![]() $\mathbb {Q}$
-Cartier divisor on
$\mathbb {Q}$
-Cartier divisor on
![]() $\mathbb {P}(q_0,\dots ,q_n)$
, which by abuse of notation we denote by
$\mathbb {P}(q_0,\dots ,q_n)$
, which by abuse of notation we denote by
![]() $\mathcal {O}_{\mathbb {P}(q_0,\dots ,q_n)}(1)$
. The lowest multiple of
$\mathcal {O}_{\mathbb {P}(q_0,\dots ,q_n)}(1)$
. The lowest multiple of
![]() $\mathcal {O}_{\mathbb {P}(q_0,\dots ,q_n)}(1)$
which is Cartier is then
$\mathcal {O}_{\mathbb {P}(q_0,\dots ,q_n)}(1)$
which is Cartier is then
![]() $\mathcal {O}_{\mathbb {P}(q_0,\dots ,q_n)}\left (\operatorname {lcm}(q_0, \dots ,q_n)\right )$
(e.g., [Reference FultonF, Prop. p. 63] or [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Exams. 4.1.5 and 4.2.11]). For the canonical bundle, using the fact that the weighted projective space is a toric variety, and that the covering map h is ramified along the toric divisors, one obtains the standard formula (e.g., [Reference DolgachevDol
Reference Abramovich, Graber and Vistoli1, Th. 3.3.4])
$\mathcal {O}_{\mathbb {P}(q_0,\dots ,q_n)}\left (\operatorname {lcm}(q_0, \dots ,q_n)\right )$
(e.g., [Reference FultonF, Prop. p. 63] or [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Exams. 4.1.5 and 4.2.11]). For the canonical bundle, using the fact that the weighted projective space is a toric variety, and that the covering map h is ramified along the toric divisors, one obtains the standard formula (e.g., [Reference DolgachevDol
Reference Abramovich, Graber and Vistoli1, Th. 3.3.4])
Thus, in our case,
and its smallest multiple that is Cartier is
![]() $4K_{\mathbb {P}(1,2,3,4,5)}$
.
$4K_{\mathbb {P}(1,2,3,4,5)}$
.
Classical invariant theory for cubic surfaces explicitly identifies the geometric divisors
![]() $D_{A_1}$
(the nodal or discriminant) and R (the Eckardt) divisors inside
$D_{A_1}$
(the nodal or discriminant) and R (the Eckardt) divisors inside
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
. For further use, we review this. By [Reference Dolgachev, van Geemen and KondoDvG, 1.3 and 6.4], the discriminant
${\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
. For further use, we review this. By [Reference Dolgachev, van Geemen and KondoDvG, 1.3 and 6.4], the discriminant
![]() $D_{A_1}$
is given by the equation
$D_{A_1}$
is given by the equation
where
![]() $I_8,I_{16}, I_{24}, I_{32}, I_{40},I_{100}$
are the standard generators of the ring of invariants of the action of
$I_8,I_{16}, I_{24}, I_{32}, I_{40},I_{100}$
are the standard generators of the ring of invariants of the action of
![]() $\operatorname {SL}(4,\mathbb {Z})$
on the space of cubics, and the subscripts denote their degrees. As
$\operatorname {SL}(4,\mathbb {Z})$
on the space of cubics, and the subscripts denote their degrees. As
![]() $I_{100}^2$
is a polynomial in the other invariants listed, these degrees show that we are working with
$I_{100}^2$
is a polynomial in the other invariants listed, these degrees show that we are working with
![]() $\mathbb {P}(8,16,24,32,40)\cong \mathbb {P}(1,2,3,4,5)$
. Moreover, the Eckardt divisor is given by
$\mathbb {P}(8,16,24,32,40)\cong \mathbb {P}(1,2,3,4,5)$
. Moreover, the Eckardt divisor is given by
![]() $I_{100}^2=0$
(e.g., [Reference Dolgachev, van Geemen and KondoDvG, §6.5]).
$I_{100}^2=0$
(e.g., [Reference Dolgachev, van Geemen and KondoDvG, §6.5]).
Pulling back the defining equation (3.6) of
![]() $D_{A_1}$
to
$D_{A_1}$
to
![]() $\mathbb {P}^4$
under the quotient map h given by (3.3), we obtain
$\mathbb {P}^4$
under the quotient map h given by (3.3), we obtain
where
![]() $y_0, \dots , y_4$
are homogeneous coordinates on
$y_0, \dots , y_4$
are homogeneous coordinates on
![]() $\mathbb {P}^4$
. Furthermore, [Reference du Plessis and WallDvG+] gives the coordinates of the point
$\mathbb {P}^4$
. Furthermore, [Reference du Plessis and WallDvG+] gives the coordinates of the point
![]() $\Delta _{3A_2}\in \mathbb {P}(1,2,3,4,5)$
as
$\Delta _{3A_2}\in \mathbb {P}(1,2,3,4,5)$
as
which in particular is a smooth point of
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
. It is also a smooth point of
${\mathcal {M}}^{\operatorname {GIT}}$
. It is also a smooth point of
![]() $D_{A_1}\subseteq \mathbb {P}(1,2,3,4,5)$
, as in the local coordinates on the open chart
$D_{A_1}\subseteq \mathbb {P}(1,2,3,4,5)$
, as in the local coordinates on the open chart
![]() $U_0\cong \mathbb {C}^4$
, the defining equation (3.6) of the discriminant divisor becomes
$U_0\cong \mathbb {C}^4$
, the defining equation (3.6) of the discriminant divisor becomes
![]() $(1-2^6z_1)^2 = 2^{14}(z_3 +2^{-3} z_2)$
, and
$(1-2^6z_1)^2 = 2^{14}(z_3 +2^{-3} z_2)$
, and
![]() $\Delta _{3A_2}$
corresponds to the point
$\Delta _{3A_2}$
corresponds to the point
![]() $(1/8^2,0,0,0)$
, so that taking partial derivatives of this equation at the point
$(1/8^2,0,0,0)$
, so that taking partial derivatives of this equation at the point
![]() $\Delta _{3A_2}$
gives smoothness of
$\Delta _{3A_2}$
gives smoothness of
![]() $D_{A_1}$
at
$D_{A_1}$
at
![]() $\Delta _{3A_2}$
.
$\Delta _{3A_2}$
.
We can perform a similar analysis for the Eckardt divisor. As mentioned above, the Eckardt divisor R is defined by
![]() $I_{100}^2$
, which is an irreducible polynomial in
$I_{100}^2$
, which is an irreducible polynomial in
![]() $I_8,\dots ,I_{40}$
. The exact expression due to Salmon for
$I_8,\dots ,I_{40}$
. The exact expression due to Salmon for
![]() $I_{100}^2$
in terms of
$I_{100}^2$
in terms of
![]() $I_8,\dots ,I_{40}$
no longer seems to be easily accessible in the literature. Dardanelli and van Geemen recently rederived it for their paper [Reference Dolgachev, van Geemen and KondoDvG], and provided us with the expression, which we have omitted to save space; for reference, it is now available on S. Casalaina-Martin’s website. From that description, one can easily see that
$I_8,\dots ,I_{40}$
no longer seems to be easily accessible in the literature. Dardanelli and van Geemen recently rederived it for their paper [Reference Dolgachev, van Geemen and KondoDvG], and provided us with the expression, which we have omitted to save space; for reference, it is now available on S. Casalaina-Martin’s website. From that description, one can easily see that
As already noted,
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
has Picard number
${\mathcal {M}}^{\operatorname {GIT}}$
has Picard number
![]() $1$
. For further reference, we collect here the classes of various Weil divisors on
$1$
. For further reference, we collect here the classes of various Weil divisors on
![]() ${\mathcal {M}}^{\operatorname {GIT}}=\mathbb {P}(1,2,3,4,5)$
:
${\mathcal {M}}^{\operatorname {GIT}}=\mathbb {P}(1,2,3,4,5)$
:
 $$ \begin{align} \begin{aligned}K_{{\mathcal {M}}^{\operatorname{GIT}}}&=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(-15), & \\ D_{A_1}&=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(4)& \text{(Discriminant divisor)},\\ R& =\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)& \text{(Eckardt divisor)}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned}K_{{\mathcal {M}}^{\operatorname{GIT}}}&=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(-15), & \\ D_{A_1}&=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(4)& \text{(Discriminant divisor)},\\ R& =\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)& \text{(Eckardt divisor)}. \end{aligned} \end{align} $$
These come from (3.5), (3.7), and (3.8), respectively. In particular, we note that the following relation holds in
![]() $\operatorname {Pic}({\mathcal {M}}^{\operatorname {GIT}})_{\mathbb {Q}}$
:
$\operatorname {Pic}({\mathcal {M}}^{\operatorname {GIT}})_{\mathbb {Q}}$
:
Remark 3.2. There is an important subtle point that we emphasize here. The divisor
![]() $\mathcal {O}_{\mathbb {P}^{19}}(1)$
on
$\mathcal {O}_{\mathbb {P}^{19}}(1)$
on
![]() $(\mathbb {P}^{19})^{ss}$
descends as a
$(\mathbb {P}^{19})^{ss}$
descends as a
![]() $\mathbb {Q}$
-divisor to the divisor
$\mathbb {Q}$
-divisor to the divisor
![]() $\frac {1}{8}\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(1)$
. The discriminant in
$\frac {1}{8}\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(1)$
. The discriminant in
![]() $(\mathbb {P}^{19})^{ss}$
has degree
$(\mathbb {P}^{19})^{ss}$
has degree
![]() $32$
(the discriminant has degree
$32$
(the discriminant has degree
![]() $(n+2)(d-1)^{n+1}$
for degree d hypersurfaces in
$(n+2)(d-1)^{n+1}$
for degree d hypersurfaces in
![]() $\mathbb {P}^{n+1}$
) and descends to the Weil divisor
$\mathbb {P}^{n+1}$
) and descends to the Weil divisor
![]() $D_{A_1}=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(4)$
on
$D_{A_1}=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(4)$
on
![]() $\mathbb {P}(1,2,3,4,5)$
. Similarly, the Eckardt divisor on
$\mathbb {P}(1,2,3,4,5)$
. Similarly, the Eckardt divisor on
![]() $(\mathbb {P}^{19})^{ss}$
has degree
$(\mathbb {P}^{19})^{ss}$
has degree
![]() $100$
(see, e.g., [Reference Dolgachev, van Geemen and KondoDvG, §6.5], or [Reference Cox, Little and SchenckCPS, Th. 4.1] for an approach that works for more general Eckardt loci) and descends as a
$100$
(see, e.g., [Reference Dolgachev, van Geemen and KondoDvG, §6.5], or [Reference Cox, Little and SchenckCPS, Th. 4.1] for an approach that works for more general Eckardt loci) and descends as a
![]() $\mathbb {Q}$
-divisor to the divisor
$\mathbb {Q}$
-divisor to the divisor
![]() $\frac {1}{2}\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)$
. However, this is not the Eckardt divisor R on
$\frac {1}{2}\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)$
. However, this is not the Eckardt divisor R on
![]() $\mathbb {P}(1,2,3,4,5)$
, which, as explained above, has class
$\mathbb {P}(1,2,3,4,5)$
, which, as explained above, has class
![]() $\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)$
. In other words, it is twice the Eckardt divisor on
$\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)$
. In other words, it is twice the Eckardt divisor on
![]() $(\mathbb {P}^{19})^{ss}$
that descends to the Eckardt divisor R on
$(\mathbb {P}^{19})^{ss}$
that descends to the Eckardt divisor R on
![]() $\mathbb {P}(1,2,3,4,5)$
. One can view this as a reflection of the fact that generic Eckardt cubic surfaces have an extra automorphism, as opposed to the case of generic cubic surfaces with an
$\mathbb {P}(1,2,3,4,5)$
. One can view this as a reflection of the fact that generic Eckardt cubic surfaces have an extra automorphism, as opposed to the case of generic cubic surfaces with an
![]() $A_1$
singularity, which do not have any extra automorphisms.
$A_1$
singularity, which do not have any extra automorphisms.
3.3 Local structure of the Kirwan blowup along the exceptional divisor
We recall some relevant computations from [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, App. C]. First, to employ the Luna Slice Theorem, we will want to understand the stabilizer of the
![]() $3A_2$
cubic surface
$3A_2$
cubic surface
![]() $S_{3A_2}$
, as well as its action on a Luna slice.
$S_{3A_2}$
, as well as its action on a Luna slice.
To begin, given a cubic surface
![]() $S\subseteq \mathbb {P}^3$
, we denote by
$S\subseteq \mathbb {P}^3$
, we denote by
![]() $\operatorname {Aut}(S)$
the automorphisms of S (which are automorphisms of S as a subvariety of
$\operatorname {Aut}(S)$
the automorphisms of S (which are automorphisms of S as a subvariety of
![]() $\mathbb {P}^3$
, and therefore we naturally have
$\mathbb {P}^3$
, and therefore we naturally have
![]() $\operatorname {Aut}(S)\subseteq \operatorname {PGL}(4,\mathbb {C})$
). From our GIT setup, we are also interested in
$\operatorname {Aut}(S)\subseteq \operatorname {PGL}(4,\mathbb {C})$
). From our GIT setup, we are also interested in
![]() $\operatorname {Stab}(S)\subseteq \operatorname {SL}(4,\mathbb {C})$
, the stabilizer subgroup, and, since it is sometimes easier to work with, we will also consider the stabilizer
$\operatorname {Stab}(S)\subseteq \operatorname {SL}(4,\mathbb {C})$
, the stabilizer subgroup, and, since it is sometimes easier to work with, we will also consider the stabilizer
![]() $\operatorname {GL}(S)\subseteq \operatorname {GL}(4,\mathbb {C})$
. We recall from [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, App. C] that the former two of these stabilizer groups for
$\operatorname {GL}(S)\subseteq \operatorname {GL}(4,\mathbb {C})$
. We recall from [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, App. C] that the former two of these stabilizer groups for
![]() $S_{3A_2}$
are two-dimensional, but we also want to work out the finite parts explicitly. To this end, we denote
$S_{3A_2}$
are two-dimensional, but we also want to work out the finite parts explicitly. To this end, we denote
an auxiliary group, and observe that there is an isomorphism
![]() $\mathbb {T}^3\cong D$
given by
$\mathbb {T}^3\cong D$
given by
![]() $(\lambda _1,\lambda _2,\lambda _3)\mapsto \operatorname {diag}(\lambda _1^{-1}\lambda _2^{-1}\lambda _3^3,\lambda _1,\lambda _2,\lambda _3)$
. We also want
$(\lambda _1,\lambda _2,\lambda _3)\mapsto \operatorname {diag}(\lambda _1^{-1}\lambda _2^{-1}\lambda _3^3,\lambda _1,\lambda _2,\lambda _3)$
. We also want
and note the isomorphism
![]() $\mathbb {T}^2\times \mu _4\cong D'$
given by
$\mathbb {T}^2\times \mu _4\cong D'$
given by
![]() $(\lambda _1,\lambda _2,i^j)\mapsto \operatorname {diag}(\lambda _1^{-1}\lambda _2^{-1}i^{3j},\lambda _1,\lambda _2,i^j)$
. To see that this map is an isomorphism, note that this certainly gives an inclusion
$(\lambda _1,\lambda _2,i^j)\mapsto \operatorname {diag}(\lambda _1^{-1}\lambda _2^{-1}i^{3j},\lambda _1,\lambda _2,i^j)$
. To see that this map is an isomorphism, note that this certainly gives an inclusion
![]() $\mathbb {T}^2\times \mu _4\hookrightarrow D'$
, and given
$\mathbb {T}^2\times \mu _4\hookrightarrow D'$
, and given
![]() $\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2,\lambda _3)\in D'$
, the two equations together give
$\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2,\lambda _3)\in D'$
, the two equations together give
![]() $\lambda _3^4=1$
, so that
$\lambda _3^4=1$
, so that
![]() $\lambda _3=i^j$
for some j. Finally, we denote
$\lambda _3=i^j$
for some j. Finally, we denote
and note the isomorphism
![]() $\mathbb {T}^2\cong D"$
given by
$\mathbb {T}^2\cong D"$
given by
![]() $(\lambda _1,\lambda _2)\mapsto \operatorname {diag}(\lambda _1^{-1}\lambda _2^{-1},\lambda _1,\lambda _2,1)$
.
$(\lambda _1,\lambda _2)\mapsto \operatorname {diag}(\lambda _1^{-1}\lambda _2^{-1},\lambda _1,\lambda _2,1)$
.
We use the notation
![]() $\mathbb {S}_3$
for the group of matrices obtained from the group of invertible diagonal
$\mathbb {S}_3$
for the group of matrices obtained from the group of invertible diagonal
![]() $3\times 3$
complex matrices by applying all possible permutations of the columns. The determination of the relevant stabilizer groups is parallel to the case of the
$3\times 3$
complex matrices by applying all possible permutations of the columns. The determination of the relevant stabilizer groups is parallel to the case of the
![]() $3D_4$
cubic threefold, treated in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, Prop. B.6], and proceeds by an explicit computation, which we put in Appendix A.1.
$3D_4$
cubic threefold, treated in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, Prop. B.6], and proceeds by an explicit computation, which we put in Appendix A.1.
Lemma 3.3 (
 $3A_2$
-stabilizer).
$3A_2$
-stabilizer).
We have:
-
1. The group
 $\operatorname {Stab}(S_{3A_2}$
is equal to (3.11)where the
$\operatorname {Stab}(S_{3A_2}$
is equal to (3.11)where the $$ \begin{align} \operatorname{Stab}(S_{3A_2})= \left\{\left( \begin{array}{c|c} \mathbb{S}_3&\\ \hline &\mathbb{C}^*\\ \end{array} \right)\in \operatorname{SL}(4,\mathbb{C}): \lambda_0\lambda_1\lambda_2=\lambda_3^3\right\}, \end{align} $$
$$ \begin{align} \operatorname{Stab}(S_{3A_2})= \left\{\left( \begin{array}{c|c} \mathbb{S}_3&\\ \hline &\mathbb{C}^*\\ \end{array} \right)\in \operatorname{SL}(4,\mathbb{C}): \lambda_0\lambda_1\lambda_2=\lambda_3^3\right\}, \end{align} $$
 $\lambda _i$
is the unique nonzero element in the ith row, and the group
$\lambda _i$
is the unique nonzero element in the ith row, and the group
 $\operatorname {GL}(S_{3A_2})$
is equal to (3.12)
$\operatorname {GL}(S_{3A_2})$
is equal to (3.12) $$ \begin{align} \operatorname{GL}(S_{3A_2}))= \left\{\left( \begin{array}{c|c} \mathbb{S}_3&\\ \hline &\mathbb{C}^*\\ \end{array} \right)\in \operatorname{GL}(4,\mathbb{C}): \lambda_0\lambda_1\lambda_2=\lambda_3^3\right\}. \end{align} $$
$$ \begin{align} \operatorname{GL}(S_{3A_2}))= \left\{\left( \begin{array}{c|c} \mathbb{S}_3&\\ \hline &\mathbb{C}^*\\ \end{array} \right)\in \operatorname{GL}(4,\mathbb{C}): \lambda_0\lambda_1\lambda_2=\lambda_3^3\right\}. \end{align} $$
-
2. There are central extensions
(3.13) $$ \begin{align} 1\to \mu_4\to \operatorname{Stab}(S_{3A_2}) \to \operatorname{Aut}(S_{3A_2})\to 1\,, \end{align} $$
(3.14)
$$ \begin{align} 1\to \mu_4\to \operatorname{Stab}(S_{3A_2}) \to \operatorname{Aut}(S_{3A_2})\to 1\,, \end{align} $$
(3.14) $$ \begin{align} 1\to \mathbb{C}^*\to \operatorname{GL}(S_{3A_2})\to \operatorname{Aut}(S_{3A_2})\to 1\,. \end{align} $$
$$ \begin{align} 1\to \mathbb{C}^*\to \operatorname{GL}(S_{3A_2})\to \operatorname{Aut}(S_{3A_2})\to 1\,. \end{align} $$
-
3. There are short exact sequences
(3.15)
with the second being split, so that there is an isomorphism
(3.16) $$ \begin{align} \operatorname{GL}(S_{3A_2})\cong D\rtimes S_3\,, \end{align} $$
$$ \begin{align} \operatorname{GL}(S_{3A_2})\cong D\rtimes S_3\,, \end{align} $$
where the action of
 $S_3$
on D is to permute the first three entries
$S_3$
on D is to permute the first three entries
 $\lambda _0,\lambda _1,\lambda _2$
.
$\lambda _0,\lambda _1,\lambda _2$
. -
4. The connected components of the groups above are
 $\operatorname {Stab}(S_{3A_2})^\circ = D"\cong \mathbb {T}^2$
,
$\operatorname {Stab}(S_{3A_2})^\circ = D"\cong \mathbb {T}^2$
,
 $\operatorname {GL}(S_{3A_2})^\circ = D\cong \mathbb {T}^3$
, and
$\operatorname {GL}(S_{3A_2})^\circ = D\cong \mathbb {T}^3$
, and
 $\operatorname {Aut}(S_{3A_2})^\circ \cong \mathbb {T}^2$
. There is a short exact sequence (3.17)
$\operatorname {Aut}(S_{3A_2})^\circ \cong \mathbb {T}^2$
. There is a short exact sequence (3.17) $$ \begin{align} 1\to \mu_4\to \operatorname{Stab}(S_{3A_2})/\operatorname{Stab}(S_{3A_2})^\circ \to S_3 \to 1\,, \end{align} $$
$$ \begin{align} 1\to \mu_4\to \operatorname{Stab}(S_{3A_2})/\operatorname{Stab}(S_{3A_2})^\circ \to S_3 \to 1\,, \end{align} $$
and we have
 $\operatorname {GL}(S_{3A_2})/\operatorname {GL}(S_{3A_2})^\circ \cong \operatorname {Aut}(S_{3A_2})/\operatorname {Aut}(S_{3A_2})^\circ \cong S_3$
.
$\operatorname {GL}(S_{3A_2})/\operatorname {GL}(S_{3A_2})^\circ \cong \operatorname {Aut}(S_{3A_2})/\operatorname {Aut}(S_{3A_2})^\circ \cong S_3$
.
We now describe the action of the stabilizer of the
![]() $S_{3A_2}$
cubic on the Luna slice. The description of the Luna slice appears in [Reference ZhangZha, p. 52], but for clarity, particularly for the action of the stabilizer, we include a discussion here as well.
$S_{3A_2}$
cubic on the Luna slice. The description of the Luna slice appears in [Reference ZhangZha, p. 52], but for clarity, particularly for the action of the stabilizer, we include a discussion here as well.
Lemma 3.4 (
 $3A_2$
-Luna slice).
$3A_2$
-Luna slice).
A Luna slice for
![]() $S_{3A_2}$
, normal to the orbit
$S_{3A_2}$
, normal to the orbit
![]() $\operatorname {SL}(4,\mathbb {C})\cdot [S_{3A_2}] \subseteq \mathbb {P}^{19}$
, is isomorphic to
$\operatorname {SL}(4,\mathbb {C})\cdot [S_{3A_2}] \subseteq \mathbb {P}^{19}$
, is isomorphic to
![]() $\mathbb {C}^6$
, spanned by the six monomials
$\mathbb {C}^6$
, spanned by the six monomials
in the tangent space
![]() $H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
.
$H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
.
The Luna slice can be projectively completed to give a
![]() $\mathbb {P}^6$
:
$\mathbb {P}^6$
:
The action of
![]() $\operatorname {Stab}(S_{3A_2})$
and
$\operatorname {Stab}(S_{3A_2})$
and
![]() $\operatorname {GL}(S_{3A2})$
on the projectively completed Luna slice is given by their inclusion into the groups
$\operatorname {GL}(S_{3A2})$
on the projectively completed Luna slice is given by their inclusion into the groups
![]() $\operatorname {SL}(4,\mathbb {C})$
and
$\operatorname {SL}(4,\mathbb {C})$
and
![]() $GL(4,\mathbb {C})$
, respectively, with the given actions of those groups on
$GL(4,\mathbb {C})$
, respectively, with the given actions of those groups on
![]() $H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
from the GIT setup.
$H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))$
from the GIT setup.
The action of
![]() $\operatorname {Stab}(S_{3A_2})$
and
$\operatorname {Stab}(S_{3A_2})$
and
![]() $\operatorname {GL}(S_{3A2})$
on the Luna slice is the natural induced action. In terms of Lemma 3.3(3) and the description in (3.15), the action of an element
$\operatorname {GL}(S_{3A2})$
on the Luna slice is the natural induced action. In terms of Lemma 3.3(3) and the description in (3.15), the action of an element
![]() $\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2,\lambda _3) $
in D or
$\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2,\lambda _3) $
in D or
![]() $D'$
is given by
$D'$
is given by
 $$ \begin{align} \begin{aligned} (\lambda_0,\lambda_1,\lambda_2,\lambda_3)&\cdot (\alpha_0,\alpha_1,\alpha_2,\alpha_{\widehat 0} ,\alpha_{\widehat 1} ,\alpha_{\widehat 2} )=\\ &=\left(\left(\frac{\lambda_0}{\lambda_3}\right)^3\alpha_0,\left(\frac{\lambda_1}{\lambda_3}\right)^3\alpha_1,\left(\frac{\lambda_2}{\lambda_3}\right)^3\alpha_2, \left(\frac{\lambda_0}{\lambda_3}\right)^2\alpha_{\widehat 0} , \left(\frac{\lambda_1}{\lambda_3}\right)^2\alpha_{\widehat 1} , \left(\frac{\lambda_2}{\lambda_3}\right)^2\alpha_{\widehat 2} \right)\,, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\lambda_0,\lambda_1,\lambda_2,\lambda_3)&\cdot (\alpha_0,\alpha_1,\alpha_2,\alpha_{\widehat 0} ,\alpha_{\widehat 1} ,\alpha_{\widehat 2} )=\\ &=\left(\left(\frac{\lambda_0}{\lambda_3}\right)^3\alpha_0,\left(\frac{\lambda_1}{\lambda_3}\right)^3\alpha_1,\left(\frac{\lambda_2}{\lambda_3}\right)^3\alpha_2, \left(\frac{\lambda_0}{\lambda_3}\right)^2\alpha_{\widehat 0} , \left(\frac{\lambda_1}{\lambda_3}\right)^2\alpha_{\widehat 1} , \left(\frac{\lambda_2}{\lambda_3}\right)^2\alpha_{\widehat 2} \right)\,, \end{aligned} \end{align} $$
and the action of
![]() $\sigma \in S_3\subseteq \operatorname {GL}(S_{3A_2})$
is given by
$\sigma \in S_3\subseteq \operatorname {GL}(S_{3A_2})$
is given by
Proof. For
![]() $S_{3A_2}=\lbrace F_{3A_2}=0\rbrace $
, the matrix
$S_{3A_2}=\lbrace F_{3A_2}=0\rbrace $
, the matrix
![]() $DF_{3A_2}$
, whose entries span the tangent space to the orbit of the
$DF_{3A_2}$
, whose entries span the tangent space to the orbit of the
![]() $3A_2$
cubic, is given by (see [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, §4.2.3] for similar computations for the
$3A_2$
cubic, is given by (see [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, §4.2.3] for similar computations for the
![]() $3D_4$
cubic threefold)
$3D_4$
cubic threefold)
 $$ \begin{align*}DF_{3A_2}=\begin{pmatrix} x_0x_1x_2&x_1^2x_2&x_1x_2^2&x_1x_2x_3\\ x_0^2x_2&x_0x_1x_2&x_0x_2^2&x_0x_2x_3\\ x_0^2x_1&x_0x_1^2&x_0x_1x_2&x_0x_1x_3\\ 3x_0x_3^2&3x_1x_3^2&3x_2x_3^2&3x_3^3\\ \end{pmatrix}\,. \end{align*} $$
$$ \begin{align*}DF_{3A_2}=\begin{pmatrix} x_0x_1x_2&x_1^2x_2&x_1x_2^2&x_1x_2x_3\\ x_0^2x_2&x_0x_1x_2&x_0x_2^2&x_0x_2x_3\\ x_0^2x_1&x_0x_1^2&x_0x_1x_2&x_0x_1x_3\\ 3x_0x_3^2&3x_1x_3^2&3x_2x_3^2&3x_3^3\\ \end{pmatrix}\,. \end{align*} $$
Since all entries of this matrix are monomial, the only possible linear relations are pairwise equalities, up to a constant factor. One sees that the only monomial that repeats more than once is
![]() $x_0x_1x_2$
, and thus all linear relations satisfied by the entries of
$x_0x_1x_2$
, and thus all linear relations satisfied by the entries of
![]() $DF_{3A_2}$
are
$DF_{3A_2}$
are
This means that the normal space to the orbit (
![]() $\dim \mathbb {P}^{19}-\dim \text { orbit } = 19-(16-3)=6$
) is spanned by the six monomials
$\dim \mathbb {P}^{19}-\dim \text { orbit } = 19-(16-3)=6$
) is spanned by the six monomials
The given action of the stabilizer on the Luna slice can be seen, for instance, from taking the Luna slice to be the affine space
then using the fact that
![]() $\lambda _0\lambda _1\lambda _2=\lambda _3^3$
, and dividing through the natural action by
$\lambda _0\lambda _1\lambda _2=\lambda _3^3$
, and dividing through the natural action by
![]() $\lambda _3^3$
, to fix the cubic form
$\lambda _3^3$
, to fix the cubic form
![]() $x_0x_1x_2+x_3^3$
in the affine space.
$x_0x_1x_2+x_3^3$
in the affine space.
We now turn to the Eckardt divisor whose generic point parameterizes smooth cubics with a nontrivial automorphism, and determine the multiplicity with which it contains
![]() $S_{3A_2}$
. The proof is by an elaborate lengthy explicit computation using the explicit form of the action on the Luna slice, and is given in Appendix A.2.
$S_{3A_2}$
. The proof is by an elaborate lengthy explicit computation using the explicit form of the action on the Luna slice, and is given in Appendix A.2.
Lemma 3.5. The Eckardt divisor
![]() $R\subseteq \mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))=\mathbb {P}^{19}$
contains the
$R\subseteq \mathbb {P} H^0(\mathbb {P}^3,\mathcal {O}_{\mathbb {P}^3}(3))=\mathbb {P}^{19}$
contains the
![]() $3A_2$
orbit
$3A_2$
orbit
![]() $\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]$
with multiplicity
$\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]$
with multiplicity
![]() $\mu =15$
; that is, if
$\mu =15$
; that is, if
![]() $\tilde \pi : \operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}\to (\mathbb {P}^{19})^{ss}$
is the blowup of the
$\tilde \pi : \operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}\to (\mathbb {P}^{19})^{ss}$
is the blowup of the
![]() $3A_2$
orbit, with exceptional divisor
$3A_2$
orbit, with exceptional divisor
![]() $D_{3A_2}$
, then
$D_{3A_2}$
, then
![]() $\tilde \pi ^*R= \widetilde R+15D_{3A_2}$
, where
$\tilde \pi ^*R= \widetilde R+15D_{3A_2}$
, where
![]() $\widetilde {R}\subset {\overline {\mathcal {B}_4/\Gamma }}$
is the strict transform of R.
$\widetilde {R}\subset {\overline {\mathcal {B}_4/\Gamma }}$
is the strict transform of R.
One can see from the above that for the action of
![]() $\operatorname {Stab}(S_{3A_2})$
on the normal space, the stabilizer of a general line will be trivial. In fact, when we blow up
$\operatorname {Stab}(S_{3A_2})$
on the normal space, the stabilizer of a general line will be trivial. In fact, when we blow up
![]() $(\mathbb {P}^{19})^{ss}$
along the orbit
$(\mathbb {P}^{19})^{ss}$
along the orbit
![]() $\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]$
in the Kirwan blowup process, then in the Luna slice, we are blowing up the origin in
$\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]$
in the Kirwan blowup process, then in the Luna slice, we are blowing up the origin in
![]() $\mathbb {C}^6$
, with exceptional divisor
$\mathbb {C}^6$
, with exceptional divisor
![]() $\mathbb {P}^5$
. The lemma above gives the action of the stabilizer on this
$\mathbb {P}^5$
. The lemma above gives the action of the stabilizer on this
![]() $\mathbb {P}^5$
.
$\mathbb {P}^5$
.
For future use, we first describe the semi-stable locus for this action of the stabilizer on
![]() $\mathbb {P}^5$
.
$\mathbb {P}^5$
.
Lemma 3.6. Denoting by
![]() $(T_0:T_1:T_2:T_{\widehat 0}:T_{\widehat 1}:T_{\widehat 2})$
the homogeneous coordinates on the exceptional divisor
$(T_0:T_1:T_2:T_{\widehat 0}:T_{\widehat 1}:T_{\widehat 2})$
the homogeneous coordinates on the exceptional divisor
![]() $\mathbb {P}^5$
of the Kirwan blowup
$\mathbb {P}^5$
of the Kirwan blowup
![]() $\operatorname {Bl}_0\mathbb {C}^6\to \mathbb {C}^6$
of the Luna slice described above, the unstable locus of the action of
$\operatorname {Bl}_0\mathbb {C}^6\to \mathbb {C}^6$
of the Luna slice described above, the unstable locus of the action of
![]() $\operatorname {GL}(S_{3A_2})$
is the union of the three codimension two loci
$\operatorname {GL}(S_{3A_2})$
is the union of the three codimension two loci
![]() $\lbrace T_0=T_{\widehat 0}=0\rbrace $
,
$\lbrace T_0=T_{\widehat 0}=0\rbrace $
,
![]() $\lbrace T_1=T_{\widehat 1}=0\rbrace $
,
$\lbrace T_1=T_{\widehat 1}=0\rbrace $
,
![]() $\lbrace T_2=T_{\widehat 2}=0\rbrace $
in
$\lbrace T_2=T_{\widehat 2}=0\rbrace $
in
![]() $\mathbb {P}^5$
.
$\mathbb {P}^5$
.
Proof. The action on the Luna slice given by (3.18) gives the following action of
![]() $\mathbb {T}^2\simeq D"=\operatorname {Aut}(S_{3A_2})^\circ $
on the
$\mathbb {T}^2\simeq D"=\operatorname {Aut}(S_{3A_2})^\circ $
on the
![]() $\mathbb {C}^6$
with coordinates T, of which the exceptional divisor is the projectivization:
$\mathbb {C}^6$
with coordinates T, of which the exceptional divisor is the projectivization:
 $$ \begin{align} \begin{aligned} (T_0,T_1,T_2,T_{\widehat 0},T_{\widehat 1},T_{\widehat 2})&\mapsto (\lambda_0^3T_0,\lambda_1^3 T_1,\lambda_2^3 T_2, \lambda_0^2T_{\widehat 0},\lambda_1^2T_{\widehat 1},\lambda_2^2T_{\widehat 2})\\ &=(\lambda_1^{-3}\lambda_2^{-3} T_0,\lambda_1^3 T_1,\lambda_2^3 T_2, \lambda_1^{-2}\lambda_2^{-2}T_{\widehat 0},\lambda_1^2T_{\widehat 1},\lambda_2^2T_{\widehat 2}) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (T_0,T_1,T_2,T_{\widehat 0},T_{\widehat 1},T_{\widehat 2})&\mapsto (\lambda_0^3T_0,\lambda_1^3 T_1,\lambda_2^3 T_2, \lambda_0^2T_{\widehat 0},\lambda_1^2T_{\widehat 1},\lambda_2^2T_{\widehat 2})\\ &=(\lambda_1^{-3}\lambda_2^{-3} T_0,\lambda_1^3 T_1,\lambda_2^3 T_2, \lambda_1^{-2}\lambda_2^{-2}T_{\widehat 0},\lambda_1^2T_{\widehat 1},\lambda_2^2T_{\widehat 2}) \end{aligned} \end{align} $$
(here we are acting by
![]() $\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2,1)$
with
$\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2,1)$
with
![]() $\lambda _0\lambda _1\lambda _2=1$
, and thus expressing
$\lambda _0\lambda _1\lambda _2=1$
, and thus expressing
![]() $\lambda _0=\lambda _1^{-1}\lambda _2^{-1}$
). The action is by multiplying each coordinate by a monomial in
$\lambda _0=\lambda _1^{-1}\lambda _2^{-1}$
). The action is by multiplying each coordinate by a monomial in
![]() $\lambda _1,\lambda _2$
, and thus
$\lambda _1,\lambda _2$
, and thus
![]() $\mathbb {C}^6$
is decomposed into a direct sum of six one-dimensional torus representations. Plotting the weights of each monomial in
$\mathbb {C}^6$
is decomposed into a direct sum of six one-dimensional torus representations. Plotting the weights of each monomial in
![]() $\mathbb {R}^2$
, a point in
$\mathbb {R}^2$
, a point in
![]() $\mathbb {C}^6$
is stable if and only if the convex hull of the set of weights corresponding to nonzero coordinates contains the origin in
$\mathbb {C}^6$
is stable if and only if the convex hull of the set of weights corresponding to nonzero coordinates contains the origin in
![]() $\mathbb {R}^2$
(e.g., [Reference Allcock and FreitagAll, Lem. 3.10] or [Reference DolgachevDol
Reference Alexeev2, Th. 12.2]). The weight diagram consists of two points on each of three rays from the origin. Thus, a convex hull of some subset of these six weights contains the origin if and only if this subset contains at least one weight from each ray. This is to say, a point is stable if and only if at least one of its two coordinates
$\mathbb {R}^2$
(e.g., [Reference Allcock and FreitagAll, Lem. 3.10] or [Reference DolgachevDol
Reference Alexeev2, Th. 12.2]). The weight diagram consists of two points on each of three rays from the origin. Thus, a convex hull of some subset of these six weights contains the origin if and only if this subset contains at least one weight from each ray. This is to say, a point is stable if and only if at least one of its two coordinates
![]() $T_0$
and
$T_0$
and
![]() $T_{\widehat 0}$
is nonzero, and so forth. Thus, the unstable points in
$T_{\widehat 0}$
is nonzero, and so forth. Thus, the unstable points in
![]() $\mathbb {C}^4\subseteq \mathbb {C}^6$
are precisely those given by a pair of equations
$\mathbb {C}^4\subseteq \mathbb {C}^6$
are precisely those given by a pair of equations
![]() $T_i=T_{\widehat i}=0$
for some i.
$T_i=T_{\widehat i}=0$
for some i.
We note that, as is the case for any Kirwan desingularization, there are no strictly semi-stable points on this exceptional divisor. We now describe the finite stabilizers along the exceptional divisor. This is another detailed explicit computation using the stabilizer computed in Lemma 3.3, and we give it in Appendix A.3. We note that the proof actually allows us to determine all possible stabilizers, but we will not need this information.
Proposition 3.7 (Stabilizers along the exceptional divisor).
Let
![]() $x\in D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
be a point in the exceptional divisor, and let
$x\in D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
be a point in the exceptional divisor, and let
![]() $S_x\subseteq \operatorname {Stab}(S_{3A_2})\subseteq \operatorname {SL}(4,\mathbb {C})$
be its stabilizer, that is, the stabilizer of a point in the exceptional divisor of
$S_x\subseteq \operatorname {Stab}(S_{3A_2})\subseteq \operatorname {SL}(4,\mathbb {C})$
be its stabilizer, that is, the stabilizer of a point in the exceptional divisor of
![]() $\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
with orbit corresponding to x.
$\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
with orbit corresponding to x.
-
1. For
 $x\in D_{3A_2}$
general,
$x\in D_{3A_2}$
general,
 $S_x=\mu _4$
(the diagonal subgroup of
$S_x=\mu _4$
(the diagonal subgroup of
 $\operatorname {SL}(4,\mathbb {C})$
).
$\operatorname {SL}(4,\mathbb {C})$
). -
2. For any
 $x\in D_{3A_2}$
, the order of
$x\in D_{3A_2}$
, the order of
 $S_x$
is not divisible by
$S_x$
is not divisible by
 $5$
.
$5$
.
Remark 3.8. The proof of Proposition 3.9, given in Appendix A.4, will provide another proof of the claim (1) of Proposition 3.7 above. There, we will even show that this assertion holds for a general point of the intersection of the strict transform
![]() $\widetilde D_{A_1}$
of the discriminant with the exceptional divisor
$\widetilde D_{A_1}$
of the discriminant with the exceptional divisor
![]() $D_{3A_2}$
. We note also that part (2) above is what will enable us to argue that the top self-intersection numbers of the canonical class on
$D_{3A_2}$
. We note also that part (2) above is what will enable us to argue that the top self-intersection numbers of the canonical class on
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are different.
${\overline {\mathcal {B}_4/\Gamma }}$
are different.
We conclude the section with the following non-transversality result.
Proposition 3.9. At a generic point of the intersection
![]() $\widetilde {D}_{A_1}\cap D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
, these two divisors do not meet transversally.
$\widetilde {D}_{A_1}\cap D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
, these two divisors do not meet transversally.
Proof Outline of the proof
The proof of this is by a detailed computation in local coordinates in charts of the blowup. To help the reader and the flow of the paper, we only summarize the key steps of the arguments here, postponing further details until Appendix A.4, where the proof will also benefit from building upon the explicit setup developed in the Appendix prior to that proof.
We first observe that the three
![]() $A_2$
singularities can be deformed independently. In the Luna slice, the deformation space of each of the
$A_2$
singularities can be deformed independently. In the Luna slice, the deformation space of each of the
![]() $A_2$
singularities is
$A_2$
singularities is
![]() $\mathbb {C}^2$
, within which the discriminant divisor
$\mathbb {C}^2$
, within which the discriminant divisor
![]() $D_{A_1}$
is a cuspidal curve. Thus, altogether in the
$D_{A_1}$
is a cuspidal curve. Thus, altogether in the
![]() $\mathbb {C}^6$
Luna slice near the
$\mathbb {C}^6$
Luna slice near the
![]() $S_{3A_2}$
cubic surface, the discriminant divisor is the product of the three equations of cubics, in three disjoint pairs of coordinates, one of which has the form
$S_{3A_2}$
cubic surface, the discriminant divisor is the product of the three equations of cubics, in three disjoint pairs of coordinates, one of which has the form
![]() $27\alpha _0^2+4\alpha _{\widehat 0} ^3=0$
.
$27\alpha _0^2+4\alpha _{\widehat 0} ^3=0$
.
To determine the local structure of the Kirwan blowup, one considers the blowup
![]() $\operatorname {Bl}_0\mathbb {C}^6$
of the origin in the Luna slice, and then studies the action of
$\operatorname {Bl}_0\mathbb {C}^6$
of the origin in the Luna slice, and then studies the action of
![]() $\mathbb {T}^2$
(the connected component of the stabilizer of
$\mathbb {T}^2$
(the connected component of the stabilizer of
![]() $S_{3A_2}$
on this blowup). Identifying the explicit four-dimensional Luna slice for this action, one writes down the equation of the discriminant divisor in this Luna slice explicitly, in charts on the projective space. In a suitable chart, this discriminant divisor (i.e., of
$S_{3A_2}$
on this blowup). Identifying the explicit four-dimensional Luna slice for this action, one writes down the equation of the discriminant divisor in this Luna slice explicitly, in charts on the projective space. In a suitable chart, this discriminant divisor (i.e., of
![]() $\widetilde {D}_{A_1}\subseteq {\mathcal {M}}^{\operatorname {K}}$
) is locally a union of a number of hypersurfaces, one of which has the form
$\widetilde {D}_{A_1}\subseteq {\mathcal {M}}^{\operatorname {K}}$
) is locally a union of a number of hypersurfaces, one of which has the form
![]() $27t_0^2+4\alpha _{\widehat 0}$
, where
$27t_0^2+4\alpha _{\widehat 0}$
, where
![]() $\alpha _{\widehat 0}=0$
is the local equation of the exceptional divisor of the blowup, that is, of
$\alpha _{\widehat 0}=0$
is the local equation of the exceptional divisor of the blowup, that is, of
![]() $D_{3A_2}$
. This intersection is manifestly non-transverse, except that extra care is needed to take care of the finite part of the stabilizer. Indeed, in principle, a quotient of a non-transverse intersection under a finite group may become transverse, and thus we need to ensure that the finite part of the stabilizer of
$D_{3A_2}$
. This intersection is manifestly non-transverse, except that extra care is needed to take care of the finite part of the stabilizer. Indeed, in principle, a quotient of a non-transverse intersection under a finite group may become transverse, and thus we need to ensure that the finite part of the stabilizer of
![]() $S_{3A_2}$
does not influence this (this is a local computation weaker than what is needed for the proof of Proposition 3.7).
$S_{3A_2}$
does not influence this (this is a local computation weaker than what is needed for the proof of Proposition 3.7).
4 The ball quotient model and the first proof of Theorem 1.1
Allcock, Carlson, and Toledo [Reference Abramovich, Graber and VistoliACT] have constructed a ball quotient model
![]() ${\mathcal {B}_4/\Gamma }$
for the moduli of cubic surfaces. They proved that the Baily–Borel compactification
${\mathcal {B}_4/\Gamma }$
for the moduli of cubic surfaces. They proved that the Baily–Borel compactification
![]() ${(\mathcal {B}_4/\Gamma )^*}$
is isomorphic to the GIT model
${(\mathcal {B}_4/\Gamma )^*}$
is isomorphic to the GIT model
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
and that under this identification the unique cusp of
${\mathcal {M}}^{\operatorname {GIT}}$
and that under this identification the unique cusp of
![]() ${(\mathcal {B}_4/\Gamma )^*}$
corresponds to the GIT boundary point
${(\mathcal {B}_4/\Gamma )^*}$
corresponds to the GIT boundary point
![]() $\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
. By the general theory, one has a toroidal compactification
$\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
. By the general theory, one has a toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
of
${\overline {\mathcal {B}_4/\Gamma }}$
of
![]() ${\mathcal {B}_4/\Gamma }$
, unique in this situation, which can be described as a blowup of
${\mathcal {B}_4/\Gamma }$
, unique in this situation, which can be described as a blowup of
![]() ${(\mathcal {B}_4/\Gamma )^*}$
at the unique cusp. Similarly to the previous section, we study the intersection of the exceptional divisor
${(\mathcal {B}_4/\Gamma )^*}$
at the unique cusp. Similarly to the previous section, we study the intersection of the exceptional divisor
![]() $T_{3A_2}$
of the blowup
$T_{3A_2}$
of the blowup
![]() ${\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
with the strict transform
${\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
with the strict transform
![]() $\widetilde {D}_n\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
of the discriminant (Heegner) divisor
$\widetilde {D}_n\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
of the discriminant (Heegner) divisor
![]() $D_n\subseteq {(\mathcal {B}_4/\Gamma )^*}$
. Here, in contrast with the Kirwan blowup where Proposition 3.9 gives non-transversality, we show in Proposition 4.10 that
$D_n\subseteq {(\mathcal {B}_4/\Gamma )^*}$
. Here, in contrast with the Kirwan blowup where Proposition 3.9 gives non-transversality, we show in Proposition 4.10 that
![]() $T_{3A_2}$
and
$T_{3A_2}$
and
![]() $\widetilde D_n$
meet generically transversally. We thus obtain a first proof of Theorem 1.1 that the isomorphism
$\widetilde D_n$
meet generically transversally. We thus obtain a first proof of Theorem 1.1 that the isomorphism
![]() ${\mathcal {M}}^{\operatorname {GIT}}-\lbrace \Delta _{3A_2}\rbrace \cong {\mathcal {B}_4/\Gamma }$
does not extend to an isomorphism of the compactifications
${\mathcal {M}}^{\operatorname {GIT}}-\lbrace \Delta _{3A_2}\rbrace \cong {\mathcal {B}_4/\Gamma }$
does not extend to an isomorphism of the compactifications
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
, despite both spaces being the blowup of the same point in
${\overline {\mathcal {B}_4/\Gamma }}$
, despite both spaces being the blowup of the same point in
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
.
${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
.
One key differentiating aspect of the ball quotient model (vs. the GIT model) is the functorial behavior with respect to marking all the lines on the cubic surfaces (i.e., with respect to the natural
![]() $W(E_6)$
cover
$W(E_6)$
cover
![]() $\mathcal {M}_m\to \mathcal {M}$
). This allows us to use Naruki’s compactification
$\mathcal {M}_m\to \mathcal {M}$
). This allows us to use Naruki’s compactification
![]() $\overline {\mathcal {N}}$
[Reference NarukiN], which is a smooth normal crossing model for the marked moduli space, in order to understand the structure of
$\overline {\mathcal {N}}$
[Reference NarukiN], which is a smooth normal crossing model for the marked moduli space, in order to understand the structure of
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
, by applying the isomorphism
${\overline {\mathcal {B}_4/\Gamma }}$
, by applying the isomorphism
![]() $\overline {\mathcal {N}}\cong \overline {{\mathcal {B}_4/\Gamma }_m}$
previously established by [Reference Gallardo, Kerr and SchafflerGKS].
$\overline {\mathcal {N}}\cong \overline {{\mathcal {B}_4/\Gamma }_m}$
previously established by [Reference Gallardo, Kerr and SchafflerGKS].
4.1 Preliminaries on the ball quotient model
We will now describe the compactifications of the ball quotient model of the moduli space of cubic surfaces. Before delving into the specifics for cubic surfaces, we first recall the compactification of ball quotients in general, referring to [Reference Ash, Mumford, Rapoport and TaiAMR+] for the general details of the constructions. Let
be an n-dimensional ball. Alternatively, we can realize
![]() $\mathcal {B}_n$
as follows. Let
$\mathcal {B}_n$
as follows. Let
![]() $\mathcal {O}$
be the ring of integers of an imaginary quadratic field
$\mathcal {O}$
be the ring of integers of an imaginary quadratic field
![]() $\mathbb {Q}(\sqrt {d})$
, and let
$\mathbb {Q}(\sqrt {d})$
, and let
![]() $\Lambda $
be a free
$\Lambda $
be a free
![]() $\mathcal {O}$
-module equipped with a Hermitian form h of signature
$\mathcal {O}$
-module equipped with a Hermitian form h of signature
![]() $(1,n)$
. Then
$(1,n)$
. Then
For an arithmetic subgroup
![]() $\Gamma \subseteq \operatorname {SU}(1,n)$
, there is a quotient quasi-projective analytic space
$\Gamma \subseteq \operatorname {SU}(1,n)$
, there is a quotient quasi-projective analytic space
![]() $\mathcal {B}_n/\Gamma $
, which by construction has at worst finite quotient singularities. This quotient admits a projective Baily–Borel compactification
$\mathcal {B}_n/\Gamma $
, which by construction has at worst finite quotient singularities. This quotient admits a projective Baily–Borel compactification
![]() $(\mathcal {B}_n/\Gamma )^*$
defined as the
$(\mathcal {B}_n/\Gamma )^*$
defined as the
![]() $\operatorname {Proj}$
of the ring of automorphic forms with respect to
$\operatorname {Proj}$
of the ring of automorphic forms with respect to
![]() $\Gamma $
. Geometrically, the boundary
$\Gamma $
. Geometrically, the boundary
![]() $(\mathcal {B}_n/\Gamma )^*-\mathcal {B}_n/\Gamma =c_{F_1}\sqcup \dots \sqcup c_{F_r}$
consists of a finite number of points, called cusps. These are in
$(\mathcal {B}_n/\Gamma )^*-\mathcal {B}_n/\Gamma =c_{F_1}\sqcup \dots \sqcup c_{F_r}$
consists of a finite number of points, called cusps. These are in
![]() $1$
-to-
$1$
-to-
![]() $1$
correspondence with the
$1$
correspondence with the
![]() $\Gamma $
-orbits of isotropic lines in
$\Gamma $
-orbits of isotropic lines in
![]() $\Lambda _{\mathbb {Q}(\sqrt {d})}$
. There are no higher-dimensional cusps since the signature is
$\Lambda _{\mathbb {Q}(\sqrt {d})}$
. There are no higher-dimensional cusps since the signature is
![]() $(1,n)$
, implying that no other isotropic subspaces exist.
$(1,n)$
, implying that no other isotropic subspaces exist.
In the case of ball quotients, there exists a unique toroidal compactification
![]() $\overline {\mathcal {B}_n/\Gamma }$
. Uniqueness follows since all tori involved have rank
$\overline {\mathcal {B}_n/\Gamma }$
. Uniqueness follows since all tori involved have rank
![]() $1$
. More precisely, after dividing by the unipotent radical of the parabolic subgroup that stabilizes a given cusp, the quotient locally looks like an open set in
$1$
. More precisely, after dividing by the unipotent radical of the parabolic subgroup that stabilizes a given cusp, the quotient locally looks like an open set in
![]() $D^* \times \mathbb {C}^{n-1} \subseteq \mathbb {C}^* \times \mathbb {C}^{n-1}$
that contains
$D^* \times \mathbb {C}^{n-1} \subseteq \mathbb {C}^* \times \mathbb {C}^{n-1}$
that contains
![]() $\{0\}\times \mathbb {C}^{n-1}$
in its closure, where here
$\{0\}\times \mathbb {C}^{n-1}$
in its closure, where here
![]() $D^*$
is the punctured unit disk. The toroidal compactification is then simply obtained by adding the divisor
$D^*$
is the punctured unit disk. The toroidal compactification is then simply obtained by adding the divisor
![]() $\{0\}\times \mathbb {C}^{n-1}$
. As a result, the boundary
$\{0\}\times \mathbb {C}^{n-1}$
. As a result, the boundary
![]() $\overline {\mathcal {B}_n/\Gamma }-\mathcal {B}_n/\Gamma =T_{F_1}\sqcup \dots \sqcup T_{F_r}$
consists of a finite disjoint union of smooth (up to finite quotient singularities) irreducible divisors, each of which is in fact a finite quotient of an abelian variety. The natural map
$\overline {\mathcal {B}_n/\Gamma }-\mathcal {B}_n/\Gamma =T_{F_1}\sqcup \dots \sqcup T_{F_r}$
consists of a finite disjoint union of smooth (up to finite quotient singularities) irreducible divisors, each of which is in fact a finite quotient of an abelian variety. The natural map
![]() $p:\overline {\mathcal {B}_n/\Gamma }\to (\mathcal {B}_n/\Gamma )^*$
simply contracts each divisor
$p:\overline {\mathcal {B}_n/\Gamma }\to (\mathcal {B}_n/\Gamma )^*$
simply contracts each divisor
![]() $T_{F_i}$
to the cusp
$T_{F_i}$
to the cusp
![]() $c_{F_i}$
(see Theorem 4.6 for a detailed discussion of the case relevant in this paper).
$c_{F_i}$
(see Theorem 4.6 for a detailed discussion of the case relevant in this paper).
With this setup, we return to the case of cubic surfaces, and describe the period map to the ball quotient. Specifically, considering the triple cover of
![]() $\mathbb {P}^3$
branched along a cubic surface, one obtains a cubic threefold, and via the period map for cubic threefolds, taking the
$\mathbb {P}^3$
branched along a cubic surface, one obtains a cubic threefold, and via the period map for cubic threefolds, taking the
![]() $\mathbb {Z}_3$
action into account, one obtains a period map to a four-dimensional ball quotient,
$\mathbb {Z}_3$
action into account, one obtains a period map to a four-dimensional ball quotient,
![]() $\mathcal {M}\rightarrow {\mathcal {B}_4/\Gamma }$
(see [Reference Abramovich, Graber and VistoliACT]). This is an open embedding, and the complement of the image is the Heegner divisor
$\mathcal {M}\rightarrow {\mathcal {B}_4/\Gamma }$
(see [Reference Abramovich, Graber and VistoliACT]). This is an open embedding, and the complement of the image is the Heegner divisor
![]() $D_n=\mathcal {D}_n/\Gamma \subseteq {\mathcal {B}_4/\Gamma }$
. It turns out that in this case the rational period map
$D_n=\mathcal {D}_n/\Gamma \subseteq {\mathcal {B}_4/\Gamma }$
. It turns out that in this case the rational period map
![]() ${\mathcal {M}}^{\operatorname {GIT}}\dashrightarrow {(\mathcal {B}_4/\Gamma )^*}$
to the Baily–Borel compactification extends to an isomorphism, taking the discriminant divisor
${\mathcal {M}}^{\operatorname {GIT}}\dashrightarrow {(\mathcal {B}_4/\Gamma )^*}$
to the Baily–Borel compactification extends to an isomorphism, taking the discriminant divisor
![]() $D_{A_1}\subseteq {\mathcal {M}}^{\operatorname {GIT}}$
to the (closure of the) Heegner divisor
$D_{A_1}\subseteq {\mathcal {M}}^{\operatorname {GIT}}$
to the (closure of the) Heegner divisor
![]() $D_n\subseteq {(\mathcal {B}_4/\Gamma )^*}$
(which is denoted this way for nodal). Under this isomorphism, the unique strictly polystable point
$D_n\subseteq {(\mathcal {B}_4/\Gamma )^*}$
(which is denoted this way for nodal). Under this isomorphism, the unique strictly polystable point
![]() $\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
corresponding to the
$\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
corresponding to the
![]() $3A_2$
cubic is identified with the sole cusp
$3A_2$
cubic is identified with the sole cusp
![]() $c_{3A_2}=\partial {(\mathcal {B}_4/\Gamma )^*}$
. The natural map
$c_{3A_2}=\partial {(\mathcal {B}_4/\Gamma )^*}$
. The natural map
![]() $p:{\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
contracts the irreducible boundary divisor
$p:{\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
contracts the irreducible boundary divisor
![]() $T_{3A_2}$
to
$T_{3A_2}$
to
![]() $c_{3A_2}$
. From now on, we will write
$c_{3A_2}$
. From now on, we will write
![]() $D_{A_1}=D_n$
for the discriminant divisor, where we use
$D_{A_1}=D_n$
for the discriminant divisor, where we use
![]() $D_{A_1}$
when we are thinking of it from the GIT point of view, and
$D_{A_1}$
when we are thinking of it from the GIT point of view, and
![]() $D_n$
when thinking of the ball quotient—to emphasize the context we are in.
$D_n$
when thinking of the ball quotient—to emphasize the context we are in.
In summary, for the case of cubic surfaces, we have a diagram

where f is a birational map that restricts to an isomorphism
In [Reference KirwanKi2] and [Reference ZhangZha], the (intersection) Betti numbers of the spaces
![]() ${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
and
${\mathcal {M}}^{\operatorname {GIT}}\cong {(\mathcal {B}_4/\Gamma )^*}$
and
![]() ${\mathcal {M}}^{\operatorname {K}}$
were computed. In [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, §C.2], the Betti numbers of
${\mathcal {M}}^{\operatorname {K}}$
were computed. In [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, §C.2], the Betti numbers of
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
were computed, and they turned out to be the same as for
${\overline {\mathcal {B}_4/\Gamma }}$
were computed, and they turned out to be the same as for
![]() ${\mathcal {M}}^{\operatorname {K}}$
, which served as motivation for our query as to whether these two compactifications are isomorphic, which is the main subject of the current paper.
${\mathcal {M}}^{\operatorname {K}}$
, which served as motivation for our query as to whether these two compactifications are isomorphic, which is the main subject of the current paper.
4.2 The toroidal compactification via marked cubic surfaces
An indispensable tool in the study of cubic surfaces is the group
![]() $W(E_6)$
, which is the automorphism group for the configuration of the
$W(E_6)$
, which is the automorphism group for the configuration of the
![]() $27$
lines on a smooth cubic. The moduli space of cubic surfaces
$27$
lines on a smooth cubic. The moduli space of cubic surfaces
![]() $\mathcal {M}$
admits a natural
$\mathcal {M}$
admits a natural
![]() $W(E_6)$
cover
$W(E_6)$
cover
![]() $\mathcal {M}_m$
parameterizing marked smooth cubic surfaces, that is, cubics together with a labeling of the
$\mathcal {M}_m$
parameterizing marked smooth cubic surfaces, that is, cubics together with a labeling of the
![]() $27$
lines. Since the automorphism group of a smooth cubic surface acts faithfully on the primitive cohomology, it follows that
$27$
lines. Since the automorphism group of a smooth cubic surface acts faithfully on the primitive cohomology, it follows that
![]() $\mathcal {M}_m$
is in fact smooth. Furthermore, Naruki [Reference NarukiN] constructed a smooth normal crossing compactification
$\mathcal {M}_m$
is in fact smooth. Furthermore, Naruki [Reference NarukiN] constructed a smooth normal crossing compactification
![]() $\overline {\mathcal {N}}$
of
$\overline {\mathcal {N}}$
of
![]() $\mathcal {M}_m$
, which admits various geometric interpretations (see, e.g., [Reference Hacking, Keel and TevelevHKT]). In this section, we use the geometry of the Naruki model
$\mathcal {M}_m$
, which admits various geometric interpretations (see, e.g., [Reference Hacking, Keel and TevelevHKT]). In this section, we use the geometry of the Naruki model
![]() $\overline {\mathcal {N}}$
to get a good hold on the space of interest in our paper,
$\overline {\mathcal {N}}$
to get a good hold on the space of interest in our paper,
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
.
${\overline {\mathcal {B}_4/\Gamma }}$
.
By construction, the marked moduli space
![]() $\mathcal {M}_m$
is a Galois cover of
$\mathcal {M}_m$
is a Galois cover of
![]() $\mathcal {M}$
with Galois group
$\mathcal {M}$
with Galois group
![]() $W(E_6)$
. This cover is compatible with the ball quotient construction of Allcock, Carlson, and Toledo [Reference Abramovich, Graber and VistoliACT]. Specifically, the monodromy group
$W(E_6)$
. This cover is compatible with the ball quotient construction of Allcock, Carlson, and Toledo [Reference Abramovich, Graber and VistoliACT]. Specifically, the monodromy group
![]() $\Gamma $
for cubic surfaces contains a normal subgroup
$\Gamma $
for cubic surfaces contains a normal subgroup
![]() $\Gamma _m\unlhd \Gamma $
with
$\Gamma _m\unlhd \Gamma $
with
(see [Reference Abramovich, Graber and VistoliACT, (3.12)]). We observe that
![]() $-1 $
acts trivially on the ball
$-1 $
acts trivially on the ball
![]() $\mathcal {B}_4$
. This leads to a
$\mathcal {B}_4$
. This leads to a
![]() $W(E_6)$
cover
$W(E_6)$
cover
![]() ${\mathcal {B}_4/\Gamma }_m\rightarrow {\mathcal {B}_4/\Gamma }$
. Furthermore, this cover extends to the Baily–Borel compactifications (cf. [Reference Abramovich, Graber and VistoliACT, Th. 3.17]), and then also to the toroidal compactifications—essentially because in the ball quotient case, the toroidal compactification is canonical, and thus there is an automatic extension. In summary, the following holds:
${\mathcal {B}_4/\Gamma }_m\rightarrow {\mathcal {B}_4/\Gamma }$
. Furthermore, this cover extends to the Baily–Borel compactifications (cf. [Reference Abramovich, Graber and VistoliACT, Th. 3.17]), and then also to the toroidal compactifications—essentially because in the ball quotient case, the toroidal compactification is canonical, and thus there is an automatic extension. In summary, the following holds:
Proposition 4.1. With notation as above, we have the following diagram:

where all the spaces in the top row admit a
![]() $W(E_6)$
action, and the morphisms are
$W(E_6)$
action, and the morphisms are
![]() $W(E_6)$
-equivariant, whereas the spaces in the bottom row are the quotients with respect to this
$W(E_6)$
-equivariant, whereas the spaces in the bottom row are the quotients with respect to this
![]() $W(E_6)$
action.
$W(E_6)$
action.
Remark 4.2. The GIT construction does not admit a natural
![]() $W(E_6)$
cover (e.g., it involves taking a quotient by
$W(E_6)$
cover (e.g., it involves taking a quotient by
![]() $\mathrm {PGL}(4,\mathbb {C})$
, which has no natural connection to
$\mathrm {PGL}(4,\mathbb {C})$
, which has no natural connection to
![]() $W(E_6)$
).
$W(E_6)$
).
Remark 4.3. We note that there is another very natural moduli space
![]() $\mathcal {M}_\ell $
parameterizing smooth cubics together with a chosen line. It is a degree 27 non-Galois cover
$\mathcal {M}_\ell $
parameterizing smooth cubics together with a chosen line. It is a degree 27 non-Galois cover
![]() $\mathcal {M}_\ell \to \mathcal {M}$
, which is in turn covered via
$\mathcal {M}_\ell \to \mathcal {M}$
, which is in turn covered via
![]() $\mathcal {M}_m\to \mathcal {M}_\ell $
. This moduli of cubics with a line is of particular interest as it has a model as a Deligne–Mostow moduli space
$\mathcal {M}_m\to \mathcal {M}_\ell $
. This moduli of cubics with a line is of particular interest as it has a model as a Deligne–Mostow moduli space
![]() $DM(2^5,1^2)$
of points on a line. As such,
$DM(2^5,1^2)$
of points on a line. As such,
![]() $\mathcal {M}_\ell $
has both a GIT compactification, and the corresponding Kirwan blowup, as of a configuration of points, and a toroidal compactification covering
$\mathcal {M}_\ell $
has both a GIT compactification, and the corresponding Kirwan blowup, as of a configuration of points, and a toroidal compactification covering
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
. It seems likely that our methods from this and previous works would make it possible to determine whether the corresponding Kirwan blowup and toroidal compactification are naturally isomorphic, but we will not pursue it here.
${\overline {\mathcal {B}_4/\Gamma }}$
. It seems likely that our methods from this and previous works would make it possible to determine whether the corresponding Kirwan blowup and toroidal compactification are naturally isomorphic, but we will not pursue it here.
It was shown recently that the marked toroidal and Naruki compactifications coincide.
Theorem 4.4 [Reference Gallardo, Kerr and SchafflerGKS].
The Naruki compactification
![]() $\overline {\mathcal {N}}$
is isomorphic to the toroidal compactification
$\overline {\mathcal {N}}$
is isomorphic to the toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
. More precisely, there is a
${\overline {\mathcal {B}_4/\Gamma _m}}$
. More precisely, there is a
![]() $W(E_6)$
-equivariant commutative diagram
$W(E_6)$
-equivariant commutative diagram

Notation 4.5. In what follows, we use freely the identification given by Theorem 4.4. Motivated by the compatibility given by diagram (4.4), we will use for
![]() ${\mathcal {B}_4/\Gamma }_m$
and its compactifications the same notation as for
${\mathcal {B}_4/\Gamma }_m$
and its compactifications the same notation as for
![]() ${\mathcal {B}_4/\Gamma }$
, simply adding the subscript m. In particular, we will consider the divisors
${\mathcal {B}_4/\Gamma }$
, simply adding the subscript m. In particular, we will consider the divisors
![]() $\widetilde D_{n,m}$
and
$\widetilde D_{n,m}$
and
![]() $T_{3A_2,m}$
on
$T_{3A_2,m}$
on
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
. We will informally refer to
${\overline {\mathcal {B}_4/\Gamma _m}}$
. We will informally refer to
![]() $\widetilde D_n$
(and
$\widetilde D_n$
(and
![]() $\widetilde D_{n,m}$
) as the nodal divisor, to
$\widetilde D_{n,m}$
) as the nodal divisor, to
![]() $\widetilde R$
(and
$\widetilde R$
(and
![]() $\widetilde R_m$
on
$\widetilde R_m$
on
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
) as the Eckardt divisor, and to
${\overline {\mathcal {B}_4/\Gamma _m}}$
) as the Eckardt divisor, and to
![]() $T_{3A_2}$
(and
$T_{3A_2}$
(and
![]() $T_{3A_2,m}$
) as the (toroidal) boundary divisor. Note that while
$T_{3A_2,m}$
) as the (toroidal) boundary divisor. Note that while
![]() $\widetilde D_n$
and
$\widetilde D_n$
and
![]() $\widetilde R$
are irreducible divisors in
$\widetilde R$
are irreducible divisors in
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
, the corresponding divisors in the marked case have several irreducible components transitively permuted by the natural
${\overline {\mathcal {B}_4/\Gamma }}$
, the corresponding divisors in the marked case have several irreducible components transitively permuted by the natural
![]() $W(E_6)$
action.
$W(E_6)$
action.
The Naruki compactification has a well-understood structure, mostly due to Naruki [Reference NarukiN], with some further later clarifications by other authors.
Theorem 4.6 (Naruki).
The spaces and maps above have the following descriptions:
-
(0)
 ${\overline {\mathcal {B}_4/\Gamma _m}}(\cong \overline {\mathcal {N}})$
is smooth, and the complement of the locus
${\overline {\mathcal {B}_4/\Gamma _m}}(\cong \overline {\mathcal {N}})$
is smooth, and the complement of the locus
 $\mathcal {M}_m$
of smooth marked cubic surfaces is the simple normal crossing divisor
$\mathcal {M}_m$
of smooth marked cubic surfaces is the simple normal crossing divisor
 $T_{3A_2,m}\cup \widetilde D_{n,m}$
.
$T_{3A_2,m}\cup \widetilde D_{n,m}$
. -
1.
-
(a) The Baily–Borel compactification
 ${(\mathcal {B}_4/\Gamma _m)^*}$
has
${(\mathcal {B}_4/\Gamma _m)^*}$
has
 $40$
cusps, permuted transitively by the
$40$
cusps, permuted transitively by the
 $W(E_6)$
action, each of which lies over the unique cusp
$W(E_6)$
action, each of which lies over the unique cusp
 $c_{3A_2}\in {(\mathcal {B}_4/\Gamma )^*}$
. Near each of the
$c_{3A_2}\in {(\mathcal {B}_4/\Gamma )^*}$
. Near each of the
 $40$
cusps,
$40$
cusps,
 ${(\mathcal {B}_4/\Gamma _m)^*}$
is locally isomorphic to the cone over
${(\mathcal {B}_4/\Gamma _m)^*}$
is locally isomorphic to the cone over
 $(\mathbb {P}^1)^{\times 3}$
embedded in
$(\mathbb {P}^1)^{\times 3}$
embedded in
 $\mathbb {P}^7$
via
$\mathbb {P}^7$
via
 $\mathcal {O}(1,1,1)$
.
$\mathcal {O}(1,1,1)$
. -
(b) The boundary divisor
 $T_{3A_2,m}\subseteq {\overline {\mathcal {B}_4/\Gamma _m}}$
has
$T_{3A_2,m}\subseteq {\overline {\mathcal {B}_4/\Gamma _m}}$
has
 $40$
disjoint irreducible components, each isomorphic to
$40$
disjoint irreducible components, each isomorphic to
 $(\mathbb {P}^1)^{\times 3}$
. The deck transformation group
$(\mathbb {P}^1)^{\times 3}$
. The deck transformation group
 $W(E_6)$
of the cover
$W(E_6)$
of the cover
 ${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
acts transitively on the set of these irreducible components.
${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
acts transitively on the set of these irreducible components.
-
-
2.
-
(a) The
 $W(E_6)$
cover
$W(E_6)$
cover
 ${(\mathcal {B}_4/\Gamma _m)^*}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
is branched along the discriminant divisor
${(\mathcal {B}_4/\Gamma _m)^*}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
is branched along the discriminant divisor
 $D_{A_1}$
and the Eckardt divisor R, with ramification index
$D_{A_1}$
and the Eckardt divisor R, with ramification index
 $2$
along each.
$2$
along each. -
(b) The
 $W(E_6)$
cover
$W(E_6)$
cover
 ${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
is generically étale along the toroidal boundary divisors
${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
is generically étale along the toroidal boundary divisors
 $T_{3A_2,m}$
.
$T_{3A_2,m}$
.
-
-
3. The stabilizer
 $S_{3A_2,m}\subseteq W(E_6)$
of an irreducible component of the divisor
$S_{3A_2,m}\subseteq W(E_6)$
of an irreducible component of the divisor
 $T_{3A_2,m}$
fits in an extension Under the identification of the irreducible component with
$T_{3A_2,m}$
fits in an extension Under the identification of the irreducible component with $$ \begin{align*} 1\to (S_3)^{\times 3}\to S_{3A_2,m}\to S_3\to 1\,. \end{align*} $$
$$ \begin{align*} 1\to (S_3)^{\times 3}\to S_{3A_2,m}\to S_3\to 1\,. \end{align*} $$
 $(\mathbb {P}^1)^{\times 3}$
, the stabilizer
$(\mathbb {P}^1)^{\times 3}$
, the stabilizer
 $S_{3A_2,m}$
acts as follows: the normal subgroup
$S_{3A_2,m}$
acts as follows: the normal subgroup
 $(S_3)^{\times 3}$
acts diagonally on
$(S_3)^{\times 3}$
acts diagonally on
 $(\mathbb {P}^1)^{\times 3}$
, whereas the residual
$(\mathbb {P}^1)^{\times 3}$
, whereas the residual
 $S_3$
acts on the quotient
$S_3$
acts on the quotient
 $(\mathbb {P}^1)^{\times 3}/(S_3)^{\times 3}\cong (\mathbb {P}(2,3))^{\times 3}\cong (\mathbb {P}^1)^{\times 3}$
by permuting the factors.
$(\mathbb {P}^1)^{\times 3}/(S_3)^{\times 3}\cong (\mathbb {P}(2,3))^{\times 3}\cong (\mathbb {P}^1)^{\times 3}$
by permuting the factors.
Proof. Item (0) is the main result of Naruki [Reference NarukiN, Th. 1]. Naruki also proved that the toroidal boundary
![]() $T_{3A_2,m}$
consists of
$T_{3A_2,m}$
consists of
![]() $40$
irreducible components (permuted transitively by
$40$
irreducible components (permuted transitively by
![]() $W(E_6)$
), each isomorphic to
$W(E_6)$
), each isomorphic to
![]() $(\mathbb {P}^1)^{\times 3}$
. The stabilizer of a boundary component and its action are discussed in [Reference NarukiN, p. 22]. In particular, items (1b), (2b), and (3) follow. As an aside, we note that each of the
$(\mathbb {P}^1)^{\times 3}$
. The stabilizer of a boundary component and its action are discussed in [Reference NarukiN, p. 22]. In particular, items (1b), (2b), and (3) follow. As an aside, we note that each of the
![]() $40$
components corresponds to a choice of embedding of the
$40$
components corresponds to a choice of embedding of the
![]() $A_2\times A_2\times A_2$
lattice into the
$A_2\times A_2\times A_2$
lattice into the
![]() $E_6$
lattice, and that intrinsically
$E_6$
lattice, and that intrinsically
![]() $S_{3A_2,m}$
is the normalizer
$S_{3A_2,m}$
is the normalizer
![]() $N_{W(E_6)}(3A_2)$
of such an embedding (recall that
$N_{W(E_6)}(3A_2)$
of such an embedding (recall that
![]() $N_{W(E_6)}(3A_2)$
is the unique, up to conjugacy, index
$N_{W(E_6)}(3A_2)$
is the unique, up to conjugacy, index
![]() $40$
subgroup of
$40$
subgroup of
![]() $W(E_6)$
; cf. [Reference CarterC, Table 9]).
$W(E_6)$
; cf. [Reference CarterC, Table 9]).
The ramification statement (2a) is clear for geometric reasons: the branch divisor consists of the nodal locus (the Picard–Lefschetz transformations act as reflections in
![]() $W(E_6)$
), and the locus of smooth cubics with extra automorphisms, which coincides with the Eckardt divisor. While the occurrence of nodal degenerations is quite general, the presence of the Eckardt component is special to cubic surfaces: it is rare for the locus of objects with extra automorphisms to form a divisor in the moduli space, and second it reflects the fact that the automorphism group of a cubic surface embeds into
$W(E_6)$
), and the locus of smooth cubics with extra automorphisms, which coincides with the Eckardt divisor. While the occurrence of nodal degenerations is quite general, the presence of the Eckardt component is special to cubic surfaces: it is rare for the locus of objects with extra automorphisms to form a divisor in the moduli space, and second it reflects the fact that the automorphism group of a cubic surface embeds into
![]() $W(E_6)$
. The ramification statement is also worked out in detail (from the ball quotient perspective) in [Reference Abramovich, Graber and VistoliACT, Ths. 2.14 and 7.26] for the nodal locus, and [Reference Abramovich, Graber and VistoliACT, §11 and Lem. 11.4] for the Eckardt locus. For the interested reader, we point out that these two types of ramification are associated, respectively, to short and long roots in the Eisenstein lattice used to construct the ball quotient model of [Reference Abramovich, Graber and VistoliACT].
$W(E_6)$
. The ramification statement is also worked out in detail (from the ball quotient perspective) in [Reference Abramovich, Graber and VistoliACT, Ths. 2.14 and 7.26] for the nodal locus, and [Reference Abramovich, Graber and VistoliACT, §11 and Lem. 11.4] for the Eckardt locus. For the interested reader, we point out that these two types of ramification are associated, respectively, to short and long roots in the Eisenstein lattice used to construct the ball quotient model of [Reference Abramovich, Graber and VistoliACT].
Finally, it remains to discuss the structure at the boundary of the Baily–Borel compactification and the relation to the toroidal compactification. First, the Baily–Borel compactification is a contraction of the toroidal boundary
![]() $T_{3A_2,m}$
in
$T_{3A_2,m}$
in
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}(\cong \overline {\mathcal {N}})$
. Thus, (1b) implies that
${\overline {\mathcal {B}_4/\Gamma _m}}(\cong \overline {\mathcal {N}})$
. Thus, (1b) implies that
![]() ${(\mathcal {B}_4/\Gamma _m)^*}$
has
${(\mathcal {B}_4/\Gamma _m)^*}$
has
![]() $40$
cusps (see also [Reference du Plessis and WallDvG+, §8.16], where this fact is proved without reference to the toroidal compactification). Since
$40$
cusps (see also [Reference du Plessis and WallDvG+, §8.16], where this fact is proved without reference to the toroidal compactification). Since
![]() $({\mathcal {B}_4/\Gamma })^*$
has a unique cusp, and the two Baily–Borel compactifications are compatible as in (4.4), the first part of (1a) follows. It remains to determine the local structure near the cusps of
$({\mathcal {B}_4/\Gamma })^*$
has a unique cusp, and the two Baily–Borel compactifications are compatible as in (4.4), the first part of (1a) follows. It remains to determine the local structure near the cusps of
![]() ${(\mathcal {B}_4/\Gamma _m)^*}$
. Naruki [Reference NarukiN, §11] constructed a contraction
${(\mathcal {B}_4/\Gamma _m)^*}$
. Naruki [Reference NarukiN, §11] constructed a contraction
![]() $ \overline {\mathcal {N}}\to \mathcal {N}^*$
of the
$ \overline {\mathcal {N}}\to \mathcal {N}^*$
of the
![]() $40$
irreducible components of
$40$
irreducible components of
![]() $T_{3A_2,m}$
to
$T_{3A_2,m}$
to
![]() $40$
singularities of the type described in (1a). It was then noted in [Reference du Plessis and WallDvG+, §2.9] that
$40$
singularities of the type described in (1a). It was then noted in [Reference du Plessis and WallDvG+, §2.9] that
![]() $\mathcal {N}^*$
coincides with
$\mathcal {N}^*$
coincides with
![]() ${(\mathcal {B}_4/\Gamma _m)^*}$
; this completes the proof.
${(\mathcal {B}_4/\Gamma _m)^*}$
; this completes the proof.
Remark 4.7. The paper [Reference Gallardo, Kerr and SchafflerGKS] proves a stronger statement than Theorem 4.4, namely that both
![]() $\overline {\mathcal N}$
and
$\overline {\mathcal N}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
are isomorphic to an appropriate Hassett moduli space of weighted stable rational curves. However, we note that in fact, Naruki’s [Reference NarukiN] results regarding the Naruki compactification
${\overline {\mathcal {B}_4/\Gamma _m}}$
are isomorphic to an appropriate Hassett moduli space of weighted stable rational curves. However, we note that in fact, Naruki’s [Reference NarukiN] results regarding the Naruki compactification
![]() $\overline {\mathcal N}$
as explained in Theorem 4.6 are enough to provide a short proof of the result of [Reference Gallardo, Kerr and SchafflerGKS] stated in Theorem 4.4. Indeed, as explained in the proof of Theorem 4.6(0) and (1.b), the union of the discriminant and Naruki boundary in
$\overline {\mathcal N}$
as explained in Theorem 4.6 are enough to provide a short proof of the result of [Reference Gallardo, Kerr and SchafflerGKS] stated in Theorem 4.4. Indeed, as explained in the proof of Theorem 4.6(0) and (1.b), the union of the discriminant and Naruki boundary in
![]() $\overline {\mathcal N}$
is a simple normal crossing divisor, and so the rational map
$\overline {\mathcal N}$
is a simple normal crossing divisor, and so the rational map
![]() $\overline {\mathcal {N}}\dashrightarrow {\overline {\mathcal {B}_4/\Gamma _m}}$
extends to a morphism (see [Reference Ash, Mumford, Rapoport and TaiAMR+]). From [Reference Abramovich, Graber and VistoliACT, Th. 3.17], the morphism is an isomorphism over the generic points of the discriminant divisor in
$\overline {\mathcal {N}}\dashrightarrow {\overline {\mathcal {B}_4/\Gamma _m}}$
extends to a morphism (see [Reference Ash, Mumford, Rapoport and TaiAMR+]). From [Reference Abramovich, Graber and VistoliACT, Th. 3.17], the morphism is an isomorphism over the generic points of the discriminant divisor in
![]() $\overline {\mathcal N}$
, mapping the discriminant in
$\overline {\mathcal N}$
, mapping the discriminant in
![]() $\overline {\mathcal N}$
to the discriminant in
$\overline {\mathcal N}$
to the discriminant in
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
. By [Reference AlexeevAF, Prop. 2.1], we know the Satake compactification
${\overline {\mathcal {B}_4/\Gamma _m}}$
. By [Reference AlexeevAF, Prop. 2.1], we know the Satake compactification
![]() ${(\mathcal {B}_4/\Gamma _m)^*}$
has
${(\mathcal {B}_4/\Gamma _m)^*}$
has
![]() $40$
cusps and thus the toroidal boundary consists of
$40$
cusps and thus the toroidal boundary consists of
![]() $40$
disjoint irreducible components. Since Naruki has shown that the Naruki boundary also consists of
$40$
disjoint irreducible components. Since Naruki has shown that the Naruki boundary also consists of
![]() $40$
disjoint irreducible components (see Theorem 4.6(1.b)), the morphism
$40$
disjoint irreducible components (see Theorem 4.6(1.b)), the morphism
![]() $\overline {\mathcal {N}}\rightarrow {\overline {\mathcal {B}_4/\Gamma _m}}$
cannot be a divisorial contraction. At the same time, since the target is
$\overline {\mathcal {N}}\rightarrow {\overline {\mathcal {B}_4/\Gamma _m}}$
cannot be a divisorial contraction. At the same time, since the target is
![]() $\mathbb Q$
-factorial, the morphism cannot be a small contraction. Hence, it is an isomorphism. Note that the reason this type of argument fails in the unmarked case, that is, the reason this type of argument does not imply that
$\mathbb Q$
-factorial, the morphism cannot be a small contraction. Hence, it is an isomorphism. Note that the reason this type of argument fails in the unmarked case, that is, the reason this type of argument does not imply that
![]() ${{\mathcal {M}}^{\operatorname {K}}}$
and
${{\mathcal {M}}^{\operatorname {K}}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are isomorphic, is that we cannot apply the Borel extension theorem since
${\overline {\mathcal {B}_4/\Gamma }}$
are isomorphic, is that we cannot apply the Borel extension theorem since
![]() ${{\mathcal {M}}^{\operatorname {K}}}$
does not have a normal crossing boundary (cf. Proposition 3.9).
${{\mathcal {M}}^{\operatorname {K}}}$
does not have a normal crossing boundary (cf. Proposition 3.9).
With these preliminaries, we can extract a series of immediate consequences on the boundary of
![]() $\mathcal {M}\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
. First, Proposition 4.1 and Theorem 4.6(0) together show that this is a normal crossing compactification in a stack sense.
$\mathcal {M}\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
. First, Proposition 4.1 and Theorem 4.6(0) together show that this is a normal crossing compactification in a stack sense.
Corollary 4.8. The boundary
![]() $\widetilde D_n\cup T_{3A_2}$
in
$\widetilde D_n\cup T_{3A_2}$
in
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
is a normal crossings divisor, up to finite quotients.
${\overline {\mathcal {B}_4/\Gamma }}$
is a normal crossings divisor, up to finite quotients.
For further reference, we also record the structure of the toroidal boundary divisor.
Corollary 4.9. The toroidal boundary divisor
![]() $T_{3A_2}\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
is isomorphic to
$T_{3A_2}\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
is isomorphic to
![]() $\mathbb {P}^3$
.
$\mathbb {P}^3$
.
Proof. The boundary divisor
![]() $T_{3A_2}$
is the quotient of a fixed component of
$T_{3A_2}$
is the quotient of a fixed component of
![]() $T_{3A_2,m}$
by the relevant stabilizer group. Using Theorem 4.6, we get
$T_{3A_2,m}$
by the relevant stabilizer group. Using Theorem 4.6, we get
![]() $T_{3A_2}\cong (\mathbb {P}^1)^{\times 3}/S_{3A_2,m}\cong \operatorname {Sym}^3\mathbb {P}^1\cong \mathbb {P}^3$
.
$T_{3A_2}\cong (\mathbb {P}^1)^{\times 3}/S_{3A_2,m}\cong \operatorname {Sym}^3\mathbb {P}^1\cong \mathbb {P}^3$
.
4.3 Proof of Theorem 1.1
At this point, we are able to establish one of our main results, namely that the period map does not extend to an isomorphism between the Kirwan compactification and the toroidal compactification of the ball quotient model. We have seen by Proposition 3.9 that the nodal and boundary divisors do not meet transversally, even generically, in the Kirwan model, whereas an immediate consequence of the above discussion is that they do so in the toroidal model.
Proposition 4.10. The discriminant
![]() $\widetilde D_n$
and boundary
$\widetilde D_n$
and boundary
![]() $T_{3A_2}$
divisors in
$T_{3A_2}$
divisors in
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
meet generically transversally along an irreducible surface.
${\overline {\mathcal {B}_4/\Gamma }}$
meet generically transversally along an irreducible surface.
Proof. This follows easily from the geometry explicitly described in Theorem 4.6 for the marked case. We first observe that the intersection of
![]() $\widetilde D_n$
and
$\widetilde D_n$
and
![]() $T_{3A_2}$
is irreducible and hence it will be enough to consider a generic point P of some component of the intersection
$T_{3A_2}$
is irreducible and hence it will be enough to consider a generic point P of some component of the intersection
![]() $ \widetilde D_{n,m}\cap T_{3A_2,m}$
. To see this, we recall that, by Theorem 4.6 (1.b), the Weyl group
$ \widetilde D_{n,m}\cap T_{3A_2,m}$
. To see this, we recall that, by Theorem 4.6 (1.b), the Weyl group
![]() $W(E_6)$
acts transitively on the cups and hence the toroidal boundary components. We fix a component T of
$W(E_6)$
acts transitively on the cups and hence the toroidal boundary components. We fix a component T of
![]() $T_{3A_2,m}$
. We claim that the stabilizer
$T_{3A_2,m}$
. We claim that the stabilizer
![]() $S_T(\cong S_{3A_2,m}$
see Theorem 4.6 (3)) of T in
$S_T(\cong S_{3A_2,m}$
see Theorem 4.6 (3)) of T in
![]() $W(E_6)$
permutes all components of
$W(E_6)$
permutes all components of
![]() $T \cap \widetilde D_{n,m}$
. For this, we recall that
$T \cap \widetilde D_{n,m}$
. For this, we recall that
![]() $T\cong (\mathbb {P}^1)^{\times 3}$
and use the description of the action of the stabilizer
$T\cong (\mathbb {P}^1)^{\times 3}$
and use the description of the action of the stabilizer
![]() $S_T$
given in Theorem 4.6(3). This stabilizer contains a normal subgroup isomorphic to
$S_T$
given in Theorem 4.6(3). This stabilizer contains a normal subgroup isomorphic to
![]() $(S_3)^{\times 3}$
acting independently on each
$(S_3)^{\times 3}$
acting independently on each
![]() $\mathbb {P}^1$
factor. There is also a residual
$\mathbb {P}^1$
factor. There is also a residual
![]() $S_3$
factor, which acts by permuting the three copies of
$S_3$
factor, which acts by permuting the three copies of
![]() $\mathbb {P}^1$
in T. The three copies of
$\mathbb {P}^1$
in T. The three copies of
![]() $(S_3)^{\times 3}$
each act on one of the copies of
$(S_3)^{\times 3}$
each act on one of the copies of
![]() $(\mathbb {P}^1)^{\times 3}$
by the projectivization of the standard action of
$(\mathbb {P}^1)^{\times 3}$
by the projectivization of the standard action of
![]() $S_3$
on
$S_3$
on
![]() $\mathbb {C}^2$
, or more intrinsically here, the projectivization of the action of
$\mathbb {C}^2$
, or more intrinsically here, the projectivization of the action of
![]() $W(A_2)$
on
$W(A_2)$
on
![]() $A_2\otimes _{\mathbb {Z}}\mathbb {C}$
, and trivially on the other two factors. Choosing suitable coordinates, we can assume that
$A_2\otimes _{\mathbb {Z}}\mathbb {C}$
, and trivially on the other two factors. Choosing suitable coordinates, we can assume that
![]() $S_3$
permutes the points
$S_3$
permutes the points
![]() $0,1,\infty $
. By [Reference NarukiN, Prop. 11.2’], the intersection
$0,1,\infty $
. By [Reference NarukiN, Prop. 11.2’], the intersection
![]() $T \cap \widetilde D_{n,m}$
consists of nine components, namely the surfaces
$T \cap \widetilde D_{n,m}$
consists of nine components, namely the surfaces
![]() $\{0\} \times (\mathbb {P}^1)^{\times 2}$
,
$\{0\} \times (\mathbb {P}^1)^{\times 2}$
,
![]() $\{1\} \times (\mathbb {P}^1)^{\times 2}$
, and
$\{1\} \times (\mathbb {P}^1)^{\times 2}$
, and
![]() $\{\infty \} \times (\mathbb {P}^1)^{\times 2}$
and their translates under the group
$\{\infty \} \times (\mathbb {P}^1)^{\times 2}$
and their translates under the group
![]() $S_3$
interchanging the three factors of
$S_3$
interchanging the three factors of
![]() $(\mathbb {P}^1)^{\times 3}$
. Clearly, these components are permuted under
$(\mathbb {P}^1)^{\times 3}$
. Clearly, these components are permuted under
![]() $S_{T}$
.
$S_{T}$
.
We can now work with the component
![]() $\{0\} \times (\mathbb {P}^1)^{\times 2}$
and recall that in
$\{0\} \times (\mathbb {P}^1)^{\times 2}$
and recall that in
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
, the divisor
${\overline {\mathcal {B}_4/\Gamma _m}}$
, the divisor
![]() $\widetilde D_{n,m}\cup T_{3A_2,m}$
has simple normal crossings. The stabilizer of a point
$\widetilde D_{n,m}\cup T_{3A_2,m}$
has simple normal crossings. The stabilizer of a point
![]() $P=(0,*_1,*_2)$
with
$P=(0,*_1,*_2)$
with
![]() $*_i \neq 0,1,\infty $
and
$*_i \neq 0,1,\infty $
and
![]() $*_1 \neq *_2$
has order
$*_1 \neq *_2$
has order
![]() $2$
; its nontrivial element is the involution in the first factor of
$2$
; its nontrivial element is the involution in the first factor of
![]() $(S_3)^{\times 3}$
which fixes
$(S_3)^{\times 3}$
which fixes
![]() $0$
and interchanges
$0$
and interchanges
![]() $1$
and
$1$
and
![]() $\infty $
. This defines a reflection in
$\infty $
. This defines a reflection in
![]() $W(E_6)$
whose fixed locus is the component of
$W(E_6)$
whose fixed locus is the component of
![]() $ \widetilde D_{n,m}$
passing through P. This involution also fixes the component T of
$ \widetilde D_{n,m}$
passing through P. This involution also fixes the component T of
![]() $T_{3A_2,m}$
(as a set, not pointwise). Thus, we can choose local analytic coordinates
$T_{3A_2,m}$
(as a set, not pointwise). Thus, we can choose local analytic coordinates
![]() $(x_1,x_2,x_3,x_4)$
on
$(x_1,x_2,x_3,x_4)$
on
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
near P such that
${\overline {\mathcal {B}_4/\Gamma _m}}$
near P such that
![]() $\widetilde D_{n,m}$
and
$\widetilde D_{n,m}$
and
![]() $T_{3A_2,m}$
are the zero loci of coordinates
$T_{3A_2,m}$
are the zero loci of coordinates
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, respectively, and such that the stabilizer acts by
$x_2$
, respectively, and such that the stabilizer acts by
![]() $x_1 \mapsto -x_1$
, leaving all other coordinates fixed. On the quotient, we can therefore take local analytic coordinates
$x_1 \mapsto -x_1$
, leaving all other coordinates fixed. On the quotient, we can therefore take local analytic coordinates
![]() $y_1=x_1^2, y_i=x_i, i= 2,3,4$
. Then locally
$y_1=x_1^2, y_i=x_i, i= 2,3,4$
. Then locally
![]() $\widetilde D_n$
and
$\widetilde D_n$
and
![]() $T_{3A_2}$
are given by
$T_{3A_2}$
are given by
![]() $y_1=0$
and
$y_1=0$
and
![]() $y_2=0$
, respectively, and the claim follows.
$y_2=0$
, respectively, and the claim follows.
Remark 4.11. In Remark 5.5, we shall provide a different proof for the fact that
![]() $W(E_6)$
acts transitively on the components of
$W(E_6)$
acts transitively on the components of
![]() $\widetilde D_{n,m}\cup T_{3A_2,m}$
.
$\widetilde D_{n,m}\cup T_{3A_2,m}$
.
Proof of Theorem 1.1
This follows immediately from Propositions 3.9 and 4.10. Indeed, these propositions show a priori that the period map does not extend to an isomorphism. However, this is enough to show that the period map does not extend to a morphism in either direction. Indeed, since f gives an isomorphism
![]() ${\mathcal {M}}^{\operatorname {K}}-D_{3A_2} \cong {\overline {\mathcal {B}_4/\Gamma }}- T_{3A_2}$
, if f extended to a morphism, it would have to send the irreducible divisor
${\mathcal {M}}^{\operatorname {K}}-D_{3A_2} \cong {\overline {\mathcal {B}_4/\Gamma }}- T_{3A_2}$
, if f extended to a morphism, it would have to send the irreducible divisor
![]() $D_{3A_2}$
to the irreducible divisor
$D_{3A_2}$
to the irreducible divisor
![]() $T_{3A_2}$
. Thus, if f were to extend to a morphism, which was not an isomorphism, it would have to be a small contraction. For a small contraction of complex varieties
$T_{3A_2}$
. Thus, if f were to extend to a morphism, which was not an isomorphism, it would have to be a small contraction. For a small contraction of complex varieties
![]() $f:Y\to X$
, if Y is quasi-projective and X is normal, then X is not
$f:Y\to X$
, if Y is quasi-projective and X is normal, then X is not
![]() $\mathbb {Q}$
-factorial (see, e.g., [Reference KollárKM, Cor. 2.63]). This would contradict the fact that
$\mathbb {Q}$
-factorial (see, e.g., [Reference KollárKM, Cor. 2.63]). This would contradict the fact that
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
is
${\overline {\mathcal {B}_4/\Gamma }}$
is
![]() $\mathbb {Q}$
-factorial, having only finite quotient singularities. A similar argument holds for the rational map
$\mathbb {Q}$
-factorial, having only finite quotient singularities. A similar argument holds for the rational map
![]() $f^{-1}$
, since
$f^{-1}$
, since
![]() ${\mathcal {M}}^{\operatorname {K}}$
is also
${\mathcal {M}}^{\operatorname {K}}$
is also
![]() $\mathbb {Q}$
-factorial.
$\mathbb {Q}$
-factorial.
As a corollary of Theorem 1.1, we have the following result, which contrasts with Corollary 4.8 for the toroidal compactification, and strengthens Proposition 3.9 (which was itself used in the proof of Theorem 1.1) for the Kirwan compactification.
Corollary 4.12. The boundary
![]() $\widetilde D_{A_1}\cup D_{3A_2}$
in
$\widetilde D_{A_1}\cup D_{3A_2}$
in
![]() ${\mathcal {M}}^{\operatorname {K}}$
is not a normal crossings divisor, even up to finite quotients.
${\mathcal {M}}^{\operatorname {K}}$
is not a normal crossings divisor, even up to finite quotients.
Proof. If the boundary
![]() $\widetilde D_{A_1}\cup D_{3A_2}$
in
$\widetilde D_{A_1}\cup D_{3A_2}$
in
![]() ${\mathcal {M}}^{\operatorname {K}}$
were a normal crossings divisor, up to finite quotients, then the standard extension theorems for period maps to toroidal compactifications [Reference Ash, Mumford, Rapoport and TaiAMR+] would imply that the period map
${\mathcal {M}}^{\operatorname {K}}$
were a normal crossings divisor, up to finite quotients, then the standard extension theorems for period maps to toroidal compactifications [Reference Ash, Mumford, Rapoport and TaiAMR+] would imply that the period map
![]() $f:{\mathcal {M}}^{\operatorname {K}}\dashrightarrow {\overline {\mathcal {B}_4/\Gamma }}$
extended to a morphism, contradicting Theorem 1.1.
$f:{\mathcal {M}}^{\operatorname {K}}\dashrightarrow {\overline {\mathcal {B}_4/\Gamma }}$
extended to a morphism, contradicting Theorem 1.1.
Remark 4.13. We emphasize that Corollary 4.12 depends on Theorem 1.1, which in turn depends on Proposition 3.9, so that the proof of Corollary 4.12 does not provide an alternate proof of Proposition 3.9. On the other hand, Theorem 1.1 follows from Theorem 1.2, whose proof is independent of Proposition 3.9. In other words, one can give an alternate proof of Proposition 3.9 by first proving Theorem 1.2, which implies Theorem 1.1, and then proving Corollary 4.12.
5 The canonical bundles of the ball quotient models
While Theorem 1.1 says that the period map does not extend to an isomorphism between
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
, a priori it is possible that
${\overline {\mathcal {B}_4/\Gamma }}$
, a priori it is possible that
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
might be abstractly isomorphic. To distinguish them, we study their canonical classes. We start with a fairly complete discussion of divisor classes (in particular the canonical class) on the ball quotient side. Similar computations occur in [Reference Casalaina-Martin and LazaCML+1, §7] for the ball quotient model for cubic threefolds. However, due to the simpler structure of the moduli of cubic surfaces, we are able to obtain sharper results here.
${\overline {\mathcal {B}_4/\Gamma }}$
might be abstractly isomorphic. To distinguish them, we study their canonical classes. We start with a fairly complete discussion of divisor classes (in particular the canonical class) on the ball quotient side. Similar computations occur in [Reference Casalaina-Martin and LazaCML+1, §7] for the ball quotient model for cubic threefolds. However, due to the simpler structure of the moduli of cubic surfaces, we are able to obtain sharper results here.
5.1 Divisors and relations in
 ${(\mathcal {B}_4/\Gamma )^*}$
${(\mathcal {B}_4/\Gamma )^*}$
The ball quotients come equipped with a natural
![]() $\mathbb {Q}$
-line bundle
$\mathbb {Q}$
-line bundle
![]() $\lambda $
, the so-called Hodge line bundle, that gives the polarization for the Baily–Borel compactification (and pulls back to a big and nef bundle on the toroidal compactification). Since
$\lambda $
, the so-called Hodge line bundle, that gives the polarization for the Baily–Borel compactification (and pulls back to a big and nef bundle on the toroidal compactification). Since
![]() ${(\mathcal {B}_4/\Gamma )^*}\cong {\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
has Picard rank
${(\mathcal {B}_4/\Gamma )^*}\cong {\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
has Picard rank
![]() $1$
, the divisors
$1$
, the divisors
![]() $\lambda $
,
$\lambda $
,
![]() $ D_n,$
and R must all be proportional. It turns out that one can express the classes of these divisors in terms of
$ D_n,$
and R must all be proportional. It turns out that one can express the classes of these divisors in terms of
![]() $\lambda $
as a consequence of the work of Borcherds. Specifically, the following holds.
$\lambda $
as a consequence of the work of Borcherds. Specifically, the following holds.
Theorem 5.1 [Reference AlexeevAF, Th. 4.7].
There is an automorphic form
![]() $\chi _4$
of weight
$\chi _4$
of weight
![]() $4$
whose divisor in
$4$
whose divisor in
![]() $\mathcal {B}_4$
is the sum of all short mirrors, each with multiplicity
$\mathcal {B}_4$
is the sum of all short mirrors, each with multiplicity
![]() $1$
. Similarly, there is an automorphic form
$1$
. Similarly, there is an automorphic form
![]() $\chi _{75}$
of weight
$\chi _{75}$
of weight
![]() $75$
whose divisor in
$75$
whose divisor in
![]() $\mathcal {B}_4$
is the sum of all long mirrors, each with multiplicity
$\mathcal {B}_4$
is the sum of all long mirrors, each with multiplicity
![]() $1$
.
$1$
.
Taking into account the ramification orders
![]() $6$
for the discriminant divisor, which corresponds to the sum of all short mirrors, and
$6$
for the discriminant divisor, which corresponds to the sum of all short mirrors, and
![]() $2$
for the Eckardt divisor, which corresponds to the sum of all long mirrors (see esp. [Reference Abramovich, Graber and VistoliACT, §11]), we obtain the following equalities in
$2$
for the Eckardt divisor, which corresponds to the sum of all long mirrors (see esp. [Reference Abramovich, Graber and VistoliACT, §11]), we obtain the following equalities in
![]() $\operatorname {Pic}_{\mathbb {Q}}({(\mathcal {B}_4/\Gamma )^*})$
:
$\operatorname {Pic}_{\mathbb {Q}}({(\mathcal {B}_4/\Gamma )^*})$
:
Similarly, in the marked case, where the map
![]() $\mathcal {B}_4\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
is only ramified along the nodal locus with index
$\mathcal {B}_4\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
is only ramified along the nodal locus with index
![]() $3$
(e.g., [Reference Abramovich, Graber and VistoliACT, Th. 7.26]), the following holds in
$3$
(e.g., [Reference Abramovich, Graber and VistoliACT, Th. 7.26]), the following holds in
![]() $\operatorname {Pic}_{\mathbb {Q}}(({\mathcal {B}_4/\Gamma }_m)^*)$
:
$\operatorname {Pic}_{\mathbb {Q}}(({\mathcal {B}_4/\Gamma }_m)^*)$
:
Under the identification
![]() ${(\mathcal {B}_4/\Gamma )^*}\cong \mathbb {P}(1,2,3,4,5)$
, we have seen (3.9) that
${(\mathcal {B}_4/\Gamma )^*}\cong \mathbb {P}(1,2,3,4,5)$
, we have seen (3.9) that
![]() $D_n=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(4)$
and
$D_n=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(4)$
and
![]() $R=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)$
(which gives
$R=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(25)$
(which gives
![]() $R=\frac {25}{4} D_n$
, agreeing with (5.1)), either of which combined with (5.1) give the following relation between the natural polarizations on
$R=\frac {25}{4} D_n$
, agreeing with (5.1)), either of which combined with (5.1) give the following relation between the natural polarizations on
![]() ${(\mathcal {B}_4/\Gamma )^*}$
and
${(\mathcal {B}_4/\Gamma )^*}$
and
![]() $\mathbb {P}(1,2,3,4,5)$
:
$\mathbb {P}(1,2,3,4,5)$
:
We now turn to the canonical divisor. By the general theory of ball quotients (e.g., [Reference Mumford, Fogarty and KirwanMum, Prop. 3.4]), this is given by a multiple of the Hodge line bundle
![]() $\lambda $
, adjusted by a contribution due to the ramification (see, e.g., [Reference AllcockAle
Reference Abramovich, Graber and Vistoli1, Th. 3.4]). The relevant multiple of
$\lambda $
, adjusted by a contribution due to the ramification (see, e.g., [Reference AllcockAle
Reference Abramovich, Graber and Vistoli1, Th. 3.4]). The relevant multiple of
![]() $\lambda $
is “
$\lambda $
is “
![]() $\dim +1$
.” We also note that
$\dim +1$
.” We also note that
![]() $\lambda $
is given by the canonical automorphy factor given by the Jacobian, and that modular forms of weight k are exactly the sections of
$\lambda $
is given by the canonical automorphy factor given by the Jacobian, and that modular forms of weight k are exactly the sections of
![]() $\lambda ^{\otimes k}$
. The ramification divisor in our case is the union of the discriminant divisor
$\lambda ^{\otimes k}$
. The ramification divisor in our case is the union of the discriminant divisor
![]() $D_n$
and the Eckardt divisor R, which have branch orders
$D_n$
and the Eckardt divisor R, which have branch orders
![]() $6$
and
$6$
and
![]() $2$
, respectively. Thus, we obtain
$2$
, respectively. Thus, we obtain
By (5.2), we see that
![]() $K_{{(\mathcal {B}_4/\Gamma )^*}}=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(-15)$
, which agrees with the canonical bundle of
$K_{{(\mathcal {B}_4/\Gamma )^*}}=\mathcal {O}_{\mathbb {P}(1,2,3,4,5)}(-15)$
, which agrees with the canonical bundle of
![]() $\mathbb {P}(1,2,3,4,5)$
(e.g., (3.9)). In the marked case, as the map
$\mathbb {P}(1,2,3,4,5)$
(e.g., (3.9)). In the marked case, as the map
![]() $\mathcal {B}_4\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
is only ramified along the nodal locus with index
$\mathcal {B}_4\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
is only ramified along the nodal locus with index
![]() $3$
, we thus obtain
$3$
, we thus obtain
The same general considerations give the formulas for the canonical bundles of the toroidal compactifications.
Proposition 5.2. The following hold:
-
1.
 $K_{{\overline {\mathcal {B}_4/\Gamma }}}=5\lambda - \frac {5}{6} \widetilde {D}_n - \frac {1}{2} \widetilde {R} - T_{3A_2}$
.
$K_{{\overline {\mathcal {B}_4/\Gamma }}}=5\lambda - \frac {5}{6} \widetilde {D}_n - \frac {1}{2} \widetilde {R} - T_{3A_2}$
. -
2.
 $K_{{\overline {\mathcal {B}_4/\Gamma _m}}}=5\lambda _m - \frac {2}{3}\widetilde {D}_{n,m} -T_{3A_2,m}$
.
$K_{{\overline {\mathcal {B}_4/\Gamma _m}}}=5\lambda _m - \frac {2}{3}\widetilde {D}_{n,m} -T_{3A_2,m}$
.
Proof. This is a standard computation, a consequence of Mumford’s Hirzebruch proportionality theorem (see, e.g., [Reference AllcockAle Reference Abramovich, Graber and Vistoli1, Th. 3.4]).
5.2 Computations of discrepancies
In order to enable us to compute the top self-intersection of the canonical class, in this section, we compute how divisors on the Baily–Borel compactifications compare to divisors on the toroidal compactifications.
Corollary 5.3. In the notation above, the canonical class is given by
Proof. By Theorem 4.6, locally near a cusp of
![]() ${(\mathcal {B}_4/\Gamma _m)^*}$
, the map
${(\mathcal {B}_4/\Gamma _m)^*}$
, the map
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
is the standard blowup of the cone over
${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
is the standard blowup of the cone over
![]() $(\mathbb {P}^1)^{\times 3}\hookrightarrow \mathbb {P}^7$
. The claim then follows by a standard computation for the blowup.
$(\mathbb {P}^1)^{\times 3}\hookrightarrow \mathbb {P}^7$
. The claim then follows by a standard computation for the blowup.
To descend to the unmarked case, we need to understand the intersection of the boundary divisor
![]() $T_{3A_2}$
with the two ramification divisors
$T_{3A_2}$
with the two ramification divisors
![]() $\widetilde D_{n,m}$
and
$\widetilde D_{n,m}$
and
![]() $\widetilde R_{m}$
.
$\widetilde R_{m}$
.
Proposition 5.4.
-
1. The normal bundle to the marked toroidal boundary divisor
 $T_{3A_2,m}$
, restricted to each irreducible boundary component, is equal to
$T_{3A_2,m}$
, restricted to each irreducible boundary component, is equal to
 $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(-1,-1,-1)$
.
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(-1,-1,-1)$
. -
2. The restriction
 $\widetilde D_{n,m}|_{T_{3A_2,m}}$
of the marked discriminant divisor to each irreducible component of the marked toroidal boundary divisor is isomorphic to
$\widetilde D_{n,m}|_{T_{3A_2,m}}$
of the marked discriminant divisor to each irreducible component of the marked toroidal boundary divisor is isomorphic to
 $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(3,3,3)$
.
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(3,3,3)$
. -
3. The restriction
 $\widetilde R_{m}|_{T_{3A_2,m}}$
of the marked Eckardt divisor to each irreducible component of the marked toroidal boundary divisor is isomorphic to
$\widetilde R_{m}|_{T_{3A_2,m}}$
of the marked Eckardt divisor to each irreducible component of the marked toroidal boundary divisor is isomorphic to
 $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(12,12,12)$
.
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(12,12,12)$
.
Proof. The same argument as in Corollary 5.3 gives the first item. As discussed in Theorem 4.6, the divisors
![]() $\widetilde D_{n,m}$
and
$\widetilde D_{n,m}$
and
![]() ${T_{3A_2,m}}$
intersect transversely, and [Reference NarukiN, Th. 11.2’] describes this intersection precisely. For a fixed irreducible component
${T_{3A_2,m}}$
intersect transversely, and [Reference NarukiN, Th. 11.2’] describes this intersection precisely. For a fixed irreducible component
![]() $T_0$
of
$T_0$
of
![]() $\widetilde T_{3A_2}$
, which we have seen is isomorphic to
$\widetilde T_{3A_2}$
, which we have seen is isomorphic to
![]() $(\mathbb {P}^1)^{\times 3}$
, the intersection of
$(\mathbb {P}^1)^{\times 3}$
, the intersection of
![]() $\widetilde D_{n,m}$
with it consists of nine irreducible components of type
$\widetilde D_{n,m}$
with it consists of nine irreducible components of type
![]() $\{\textrm {pt}\}\times \mathbb {P}^1\times \mathbb {P}^1\subseteq \mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1$
, and thus of class
$\{\textrm {pt}\}\times \mathbb {P}^1\times \mathbb {P}^1\subseteq \mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1$
, and thus of class
![]() $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,0,0)$
(up to permuting the coordinates). The claim (2) thus follows.
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,0,0)$
(up to permuting the coordinates). The claim (2) thus follows.
The stabilizer
![]() $S_{3A_2,m}\subseteq W(E_6)$
of
$S_{3A_2,m}\subseteq W(E_6)$
of
![]() $T_0$
was identified in Theorem 4.6. Taking
$T_0$
was identified in Theorem 4.6. Taking
![]() $U_m$
to be a suitable invariant neighborhood of
$U_m$
to be a suitable invariant neighborhood of
![]() $T_0$
, locally near
$T_0$
, locally near
![]() $T_0$
, the map
$T_0$
, the map
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
is simply the quotient
${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
is simply the quotient
![]() $U_m\to U_m/S_{3A_2,m}\cong U$
, with U a neighborhood of the toroidal boundary
$U_m\to U_m/S_{3A_2,m}\cong U$
, with U a neighborhood of the toroidal boundary
![]() $T_{3A_2}\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
. Since
$T_{3A_2}\subseteq {\overline {\mathcal {B}_4/\Gamma }}$
. Since
![]() $S_{3A_2,m}$
contains a normal subgroup
$S_{3A_2,m}$
contains a normal subgroup
![]() $(S_3)^{\times 3}$
, we can take the intermediate quotient
$(S_3)^{\times 3}$
, we can take the intermediate quotient
![]() $U'=U_m/(S_3)^{\times 3}$
and obtain a diagram
$U'=U_m/(S_3)^{\times 3}$
and obtain a diagram

compatible with Theorem 4.6(3) and Corollary 4.9. Let
![]() $T'\subseteq U'$
be the quotient
$T'\subseteq U'$
be the quotient
![]() $T_0/((S_3)^{\times 3})\cong (\mathbb {P}(2,3))^{\times 3}\cong (\mathbb {P}^1)^{\times 3}$
.
$T_0/((S_3)^{\times 3})\cong (\mathbb {P}(2,3))^{\times 3}\cong (\mathbb {P}^1)^{\times 3}$
.
To describe
![]() $\widetilde R_{m}\cap T_0$
, first recall that
$\widetilde R_{m}\cap T_0$
, first recall that
![]() $U_m\to U$
is ramified along the Eckardt and nodal loci, with order
$U_m\to U$
is ramified along the Eckardt and nodal loci, with order
![]() $2$
along each. The factorization
$2$
along each. The factorization
![]() $U_m\xrightarrow {\alpha } U'\xrightarrow {\beta } U$
has the property that
$U_m\xrightarrow {\alpha } U'\xrightarrow {\beta } U$
has the property that
![]() $\alpha $
is ramified along the nodal locus, whereas
$\alpha $
is ramified along the nodal locus, whereas
![]() $\beta $
is ramified along the Eckardt locus. Indeed, in the language of [Reference Abramovich, Graber and VistoliACT], the subgroup
$\beta $
is ramified along the Eckardt locus. Indeed, in the language of [Reference Abramovich, Graber and VistoliACT], the subgroup
![]() $(S_3)^{\times 3}\subseteq S_ {3A_2,m}$
is generated by short roots (corresponding to the nine nodal components meeting
$(S_3)^{\times 3}\subseteq S_ {3A_2,m}$
is generated by short roots (corresponding to the nine nodal components meeting
![]() $T_0$
), and the residual
$T_0$
), and the residual
![]() $S_3=S_ {3A_2,m}/(S_3)^{\times 3}$
is generated by classes of long roots (corresponding to the Eckardt locus, and geometrically to cubics with an extra involution). In this description, it is clear that the restriction of the Eckardt locus to
$S_3=S_ {3A_2,m}/(S_3)^{\times 3}$
is generated by classes of long roots (corresponding to the Eckardt locus, and geometrically to cubics with an extra involution). In this description, it is clear that the restriction of the Eckardt locus to
![]() $T'$
is simply the sum of the three small diagonals (each of type
$T'$
is simply the sum of the three small diagonals (each of type
![]() $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,1,0)$
, up to permutation), and thus of class
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,1,0)$
, up to permutation), and thus of class
![]() $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(2,2,2)$
. The pullback via
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(2,2,2)$
. The pullback via
![]() $\alpha _{\mid T_0}$
of this class will be of type
$\alpha _{\mid T_0}$
of this class will be of type
![]() $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(12,12,12)$
. Since
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(12,12,12)$
. Since
![]() $\alpha $
is not ramified along the Eckardt locus, this will be also the class of the reduced divisor
$\alpha $
is not ramified along the Eckardt locus, this will be also the class of the reduced divisor
![]() $\widetilde {R}_{m}|_{T_0}$
.
$\widetilde {R}_{m}|_{T_0}$
.
Remark 5.5. The last two claims in Proposition 5.4 can be obtained also by a purely arithmetic argument. As alluded to in the proofs above, they follow by counting the short and long roots incident to a fixed cusp in
![]() ${(\mathcal {B}_4/\Gamma _m)^*}$
. To explain this, we consider the vector space
${(\mathcal {B}_4/\Gamma _m)^*}$
. To explain this, we consider the vector space
![]() $\mathbb {F}_3^5$
, equipped with the standard orthogonal form of signature
$\mathbb {F}_3^5$
, equipped with the standard orthogonal form of signature
![]() $(4,1)$
. It is well known that the orthogonal group can then be identified as
$(4,1)$
. It is well known that the orthogonal group can then be identified as
An element
![]() $[w] \in \mathbb {P}(\mathbb {F}_3^5)$
is called isotropic, short, or long, depending on whether the norm of w equals
$[w] \in \mathbb {P}(\mathbb {F}_3^5)$
is called isotropic, short, or long, depending on whether the norm of w equals
![]() $0,1$
, or
$0,1$
, or
![]() $2$
(this does not depend on the chosen representative in
$2$
(this does not depend on the chosen representative in
![]() $\mathbb {F}_3^5$
). By [Reference AlexeevAF, §2] (also [Reference Abramovich, Graber and VistoliACT]), these elements enumerate the cusps, the components of the discriminant divisor
$\mathbb {F}_3^5$
). By [Reference AlexeevAF, §2] (also [Reference Abramovich, Graber and VistoliACT]), these elements enumerate the cusps, the components of the discriminant divisor
![]() $\widetilde D_{n,m}$
, and of the Eckardt divisor
$\widetilde D_{n,m}$
, and of the Eckardt divisor
![]() $\widetilde R_{m}$
, respectively. We further know from [Reference AlexeevAF, Prop. 2.1] that there are
$\widetilde R_{m}$
, respectively. We further know from [Reference AlexeevAF, Prop. 2.1] that there are
![]() $40$
isotropic,
$40$
isotropic,
![]() $36$
short, and
$36$
short, and
![]() $45$
long elements in
$45$
long elements in
![]() $ \mathbb {P}(\mathbb {F}_3^5)$
, and that the Weyl group
$ \mathbb {P}(\mathbb {F}_3^5)$
, and that the Weyl group
![]() $W(E_6)$
acts transitively on each of these three sets.
$W(E_6)$
acts transitively on each of these three sets.
Counting the number of components of the discriminant divisor
![]() $\widetilde D_{n,m}$
and of the Eckardt divisor
$\widetilde D_{n,m}$
and of the Eckardt divisor
![]() $\widetilde R_{m}$
intersecting an irreducible component
$\widetilde R_{m}$
intersecting an irreducible component
![]() $T_0$
of
$T_0$
of
![]() $T_{3A_2,m}$
as above is then an easy enumeration. Indeed, the choice of the cusp, and of
$T_{3A_2,m}$
as above is then an easy enumeration. Indeed, the choice of the cusp, and of
![]() $T_0$
, means fixing an isotropic element
$T_0$
, means fixing an isotropic element
![]() $h\in \mathbb {P}(\mathbb {F}_3^5)$
, and a straightforward count shows that there are
$h\in \mathbb {P}(\mathbb {F}_3^5)$
, and a straightforward count shows that there are
![]() $9$
short and
$9$
short and
![]() $18$
long vectors orthogonal to h, which counts the number of irreducible components of
$18$
long vectors orthogonal to h, which counts the number of irreducible components of
![]() $\widetilde {D}_{n,m}$
and
$\widetilde {D}_{n,m}$
and
![]() $\widetilde {R}_m$
that intersect
$\widetilde {R}_m$
that intersect
![]() $T_0$
.
$T_0$
.
To describe the intersection of these components of
![]() $\widetilde D_{n,m}$
and
$\widetilde D_{n,m}$
and
![]() $\widetilde R_{m}$
with
$\widetilde R_{m}$
with
![]() $T_0$
, note that since the stabilizer subgroup of h in
$T_0$
, note that since the stabilizer subgroup of h in
![]() $W(E_6)$
acts transitively on the set of all sort (and also on the set of all long) vectors orthogonal to h, by symmetry it is enough to understand the intersection with
$W(E_6)$
acts transitively on the set of all sort (and also on the set of all long) vectors orthogonal to h, by symmetry it is enough to understand the intersection with
![]() $T_0$
of only one component of
$T_0$
of only one component of
![]() $\widetilde D_{n,m}$
and one component of
$\widetilde D_{n,m}$
and one component of
![]() $\widetilde R_{m}$
with
$\widetilde R_{m}$
with
![]() $T_0$
, which can be seen, for example, from the standard local coordinates near a boundary component. All we need is then to understand the involutions which account for the degree
$T_0$
, which can be seen, for example, from the standard local coordinates near a boundary component. All we need is then to understand the involutions which account for the degree
![]() $2$
ramification along
$2$
ramification along
![]() $\widetilde D_n$
and
$\widetilde D_n$
and
![]() $\widetilde R$
. In the case of the nodal divisor, this is, up to symmetry, an involution on a factor
$\widetilde R$
. In the case of the nodal divisor, this is, up to symmetry, an involution on a factor
![]() $\mathbb {P}^1$
which fixes some point
$\mathbb {P}^1$
which fixes some point
![]() $p\in \mathbb {P}^1$
, and then the restriction of the component of
$p\in \mathbb {P}^1$
, and then the restriction of the component of
![]() $\widetilde D_{n,m}$
to
$\widetilde D_{n,m}$
to
![]() $T_0$
, fixed under this involution, is
$T_0$
, fixed under this involution, is
![]() $p \times (\mathbb {P}^1)^{\times 2}$
, which gives the divisor class
$p \times (\mathbb {P}^1)^{\times 2}$
, which gives the divisor class
![]() $ \mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,0,0)$
. Adding up all nine components of
$ \mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,0,0)$
. Adding up all nine components of
![]() $\widetilde D_{n,m}$
that meet
$\widetilde D_{n,m}$
that meet
![]() $T_0$
, we obtain
$T_0$
, we obtain
![]() $ \mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(3,3,3)$
. In the case of the Eckardt divisor, the involution is given by interchanging two of the factors of
$ \mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(3,3,3)$
. In the case of the Eckardt divisor, the involution is given by interchanging two of the factors of
![]() $(\mathbb {P}^1)^{\times 3}$
, while fixing the third factor. In the case of interchanging the first two factors, the fixed locus is then equal to
$(\mathbb {P}^1)^{\times 3}$
, while fixing the third factor. In the case of interchanging the first two factors, the fixed locus is then equal to
![]() $\Delta _{3A_2,12} \times \mathbb {P}^1$
, and has class
$\Delta _{3A_2,12} \times \mathbb {P}^1$
, and has class
![]() $ \mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,1,0)$
. Summing over all
$ \mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(1,1,0)$
. Summing over all
![]() $18$
components of
$18$
components of
![]() $\widetilde R_m$
which meet
$\widetilde R_m$
which meet
![]() $T_0$
, we obtain
$T_0$
, we obtain
![]() $\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(12,12,12)$
.
$\mathcal {O}_{(\mathbb {P}^1)^{\times 3}}(12,12,12)$
.
We can now compare the discrepancies in the pullbacks of the discriminant and Eckardt divisors for the moduli of marked cubic surfaces.
Corollary 5.6. Let
![]() $p_m^*:{\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
be the natural map. The following hold:
$p_m^*:{\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
be the natural map. The following hold:
-
1.
 $p_m^* D_{n,m} = \widetilde D_{n,m}+3T_{3A_2,m}$
.
$p_m^* D_{n,m} = \widetilde D_{n,m}+3T_{3A_2,m}$
. -
2.
 $p_m^* R_m = \widetilde R_m + 12 T_{3A_2,m}$
.
$p_m^* R_m = \widetilde R_m + 12 T_{3A_2,m}$
.
Proof. This follows immediately from Proposition 5.4, by restricting to
![]() $T_{3A_2,m}$
. Indeed, a priori we have
$T_{3A_2,m}$
. Indeed, a priori we have
![]() $p_m^* D_{n,m} = \widetilde D_{n,m}+aT_{3A_2,m}$
for some a, and restricting to the component
$p_m^* D_{n,m} = \widetilde D_{n,m}+aT_{3A_2,m}$
for some a, and restricting to the component
![]() $T_0$
of
$T_0$
of
![]() $T_{3A_2,m}$
gives
$T_{3A_2,m}$
gives
![]() $0= \widetilde D_{n,m}|_{T_0}+ aT_{3A_2,m}|_{T_0}$
, which gives
$0= \widetilde D_{n,m}|_{T_0}+ aT_{3A_2,m}|_{T_0}$
, which gives
![]() $a=3$
by parts (1) and (2) of Proposition 5.4. The computation for the Eckardt divisor is identical using parts (1) and (3).
$a=3$
by parts (1) and (2) of Proposition 5.4. The computation for the Eckardt divisor is identical using parts (1) and (3).
Remark 5.7. It is interesting to note that the formulas above are compatible with those of Proposition 5.2 that were obtained by general considerations. Specifically, using (5.4) and Corollaries 5.3 and 5.6, we get
 $$ \begin{align*} K_{{\overline{\mathcal {B}_4/\Gamma _m}}}&=p_m^*K_{{(\mathcal {B}_4/\Gamma _m)^*}}+T_{3A_2,m}\\&= 5\lambda -\frac{2}{3} (\widetilde{D}_{n,m}+3T_{3A_2,m})+T_{3A_2,m}\\&= 5\lambda -\frac{2}{3} \widetilde{D}_{n,m}-T_{3A_2,m}\,, \end{align*} $$
$$ \begin{align*} K_{{\overline{\mathcal {B}_4/\Gamma _m}}}&=p_m^*K_{{(\mathcal {B}_4/\Gamma _m)^*}}+T_{3A_2,m}\\&= 5\lambda -\frac{2}{3} (\widetilde{D}_{n,m}+3T_{3A_2,m})+T_{3A_2,m}\\&= 5\lambda -\frac{2}{3} \widetilde{D}_{n,m}-T_{3A_2,m}\,, \end{align*} $$
agreeing indeed with Proposition 5.2(2).
The main result of this section is the computation of the discrepancy of
![]() $p^*:{\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
in the unmarked case, as this coefficient will be crucial for computing the top self-intersection number of
$p^*:{\overline {\mathcal {B}_4/\Gamma }}\rightarrow {(\mathcal {B}_4/\Gamma )^*}$
in the unmarked case, as this coefficient will be crucial for computing the top self-intersection number of
![]() $K_{{\overline {\mathcal {B}_4/\Gamma }}}$
.
$K_{{\overline {\mathcal {B}_4/\Gamma }}}$
.
Proposition 5.8. The canonical bundle of the toroidal compactification of the ball quotient model of the moduli space of cubic surfaces is given by the formula:
Proof. Since in (4.4) we computed the discrepancy for the finite cover
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
, a standard computation (see, e.g., [Reference Kollár and MoriKo
Reference Alexeev2, 2.3]) gives
${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {(\mathcal {B}_4/\Gamma _m)^*}$
, a standard computation (see, e.g., [Reference Kollár and MoriKo
Reference Alexeev2, 2.3]) gives
for
 $$ \begin{align*} a= \frac{1}{r(T_{3A_2,m})}\left((1+\mu_{\widetilde D_{n,m}}+\mu_{\widetilde R_m})+1)\right)-1\,, \end{align*} $$
$$ \begin{align*} a= \frac{1}{r(T_{3A_2,m})}\left((1+\mu_{\widetilde D_{n,m}}+\mu_{\widetilde R_m})+1)\right)-1\,, \end{align*} $$
where
![]() $r(T_{3A_2,m})=1$
is the ramification index for the cover
$r(T_{3A_2,m})=1$
is the ramification index for the cover
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
along the toroidal boundary divisor (Theorem 4.6(4)), and
${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
along the toroidal boundary divisor (Theorem 4.6(4)), and
![]() $\mu _{\widetilde D_{n,m}}=3$
and
$\mu _{\widetilde D_{n,m}}=3$
and
![]() $\mu _{\widetilde R_m}=12 $
are defined so that
$\mu _{\widetilde R_m}=12 $
are defined so that
![]() $p_m^* D_{n,m} = \widetilde D_{n,m}+\mu _{\widetilde D_{n,m}}T_{3A_2,m}$
and
$p_m^* D_{n,m} = \widetilde D_{n,m}+\mu _{\widetilde D_{n,m}}T_{3A_2,m}$
and
![]() $p_m^* R_m = \widetilde R_m + \mu _{\widetilde R_m} T_{3A_2,m}$
(Corollary 5.6). We conclude that
$p_m^* R_m = \widetilde R_m + \mu _{\widetilde R_m} T_{3A_2,m}$
(Corollary 5.6). We conclude that
![]() $a= ((1+3+12) +1)-1=16$
as claimed.
$a= ((1+3+12) +1)-1=16$
as claimed.
Remark 5.9. For completeness, we note that the analog of Corollary 5.6 in the unmarked case is
Similarly to Remark 5.7, these formulas are compatible with Propositions 5.8 and 5.2(1) and (5.3), giving a double check of our computations.
5.3 Self-intersection numbers for the toroidal compactification
Using the fact that the Baily–Borel compactification is a weighted projective space
![]() ${(\mathcal {B}_4/\Gamma )^*}\cong {\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
, and (5.2), we conclude the following.
${(\mathcal {B}_4/\Gamma )^*}\cong {\mathcal {M}}^{\operatorname {GIT}}\cong \mathbb {P}(1,2,3,4,5)$
, and (5.2), we conclude the following.
Corollary 5.10. On
![]() ${(\mathcal {B}_4/\Gamma )^*}$
, the following holds:
${(\mathcal {B}_4/\Gamma )^*}$
, the following holds:
 $$ \begin{align*}\left(K_{{(\mathcal {B}_4/\Gamma )^*}}\right)^4=\frac{(-15)^4}{5!}=\frac{15^3}{2^3}=\frac{3,375}{8}\end{align*} $$
$$ \begin{align*}\left(K_{{(\mathcal {B}_4/\Gamma )^*}}\right)^4=\frac{(-15)^4}{5!}=\frac{15^3}{2^3}=\frac{3,375}{8}\end{align*} $$
and
![]() $\lambda ^4=\frac {1}{5!\cdot 6^4}=\frac {1}{2^73^55}=\frac {1}{155,520}$
.
$\lambda ^4=\frac {1}{5!\cdot 6^4}=\frac {1}{2^73^55}=\frac {1}{155,520}$
.
Using the description of toroidal boundary given by Theorem 4.6, we obtain the following.
Lemma 5.11. The self-intersection numbers of the toroidal boundary divisors are
Proof. By Theorem 4.6, each component of
![]() $T_{3A_2,m}$
is the exceptional divisor of the standard blowup of the cone over the Segre embedding
$T_{3A_2,m}$
is the exceptional divisor of the standard blowup of the cone over the Segre embedding
![]() $(\mathbb {P}^1)^{\times 3}\hookrightarrow \mathbb {P}^7$
. It follows that the self-intersection of each such component in
$(\mathbb {P}^1)^{\times 3}\hookrightarrow \mathbb {P}^7$
. It follows that the self-intersection of each such component in
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}$
is
${\overline {\mathcal {B}_4/\Gamma _m}}$
is
![]() $-6$
. Taking into account that there are
$-6$
. Taking into account that there are
![]() $40$
disjoint such components, the first item follows. The degree of the map
$40$
disjoint such components, the first item follows. The degree of the map
![]() ${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
is
${\overline {\mathcal {B}_4/\Gamma _m}}\rightarrow {\overline {\mathcal {B}_4/\Gamma }}$
is
![]() $51,840=|W(E_6)|$
, and since this covering map is unramified along
$51,840=|W(E_6)|$
, and since this covering map is unramified along
![]() $T_{3A_2}$
, the second claim follows.
$T_{3A_2}$
, the second claim follows.
Finally, we can compute the top degree self-intersection of the canonical class on the toroidal compactification.
Theorem 5.12. The top self-intersection number of the canonical class on
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
is
${\overline {\mathcal {B}_4/\Gamma }}$
is
6 The canonical bundle of Kirwan desingularizations
For addressing the issue of K-equivalence of the compactifications, we now need to perform the computations on the GIT side parallel to the ball quotient computations in the previous section. These turn out to be more involved, and we devote this section to the general setup and results on computing the canonical bundle of the Kirwan resolution of a GIT quotient. This does not seem to be available in the literature, and may be of independent interest. After discussing the general case, we specialize to the case of cubic surfaces in §6.4.
6.1 Setup
We start with the general setup of a GIT triple
![]() $(X,L,G)$
, where X is a scheme of finite type (we will continue to work over
$(X,L,G)$
, where X is a scheme of finite type (we will continue to work over
![]() $\mathbb {C}$
to simplify notation, but the argument works over any algebraically closed field of characteristic zero, and, with minor adjustments, in positive characteristic, as well), L is an ample line bundle on X, and G is a connected reductive linear algebraic group acting on X, with L being G-linearized. We will also make the following assumptions that put us into the setup for Kirwan’s work:
$\mathbb {C}$
to simplify notation, but the argument works over any algebraically closed field of characteristic zero, and, with minor adjustments, in positive characteristic, as well), L is an ample line bundle on X, and G is a connected reductive linear algebraic group acting on X, with L being G-linearized. We will also make the following assumptions that put us into the setup for Kirwan’s work:
-
• X is a smooth quasi-projective variety.
-
•
 $X^s \ne \emptyset $
, that is, the stable locus is nonempty.
$X^s \ne \emptyset $
, that is, the stable locus is nonempty.
Note that from the second condition, and say the Luna Slice Theorem, it follows that there are a Zariski dense open subvariety
![]() $U\subseteq X^s$
and a finite group
$U\subseteq X^s$
and a finite group
![]() $G_X$
such that for all
$G_X$
such that for all
![]() $x\in U$
the stabilizer
$x\in U$
the stabilizer
![]() $G_x\subseteq G$
is isomorphic (although not necessarily equal) to
$G_x\subseteq G$
is isomorphic (although not necessarily equal) to
![]() $G_X$
; that is,
$G_X$
; that is,
![]() $G_X$
is the stabilizer of some general point of X.
$G_X$
is the stabilizer of some general point of X.
We denote by
the GIT quotient.
6.2 Canonical classes for GIT quotients
Since
![]() $X^{ss}$
is normal, so is Y (e.g, [Reference DolgachevDol
Reference Alexeev2, Prop. 3.1, p. 45]), and so canonical classes
$X^{ss}$
is normal, so is Y (e.g, [Reference DolgachevDol
Reference Alexeev2, Prop. 3.1, p. 45]), and so canonical classes
![]() $K_{X^{ss}}$
and
$K_{X^{ss}}$
and
![]() $K_Y$
are defined. Note that while
$K_Y$
are defined. Note that while
![]() $K_{X^{ss}}$
is Cartier, recall that there are elementary examples of quotients of smooth varieties by reductive groups that are not
$K_{X^{ss}}$
is Cartier, recall that there are elementary examples of quotients of smooth varieties by reductive groups that are not
![]() $\mathbb {Q}$
-Gorenstein (e.g., [Reference Braun, Greb, Langlois and MoragaBGL+, Exam.7.1]); in other words,
$\mathbb {Q}$
-Gorenstein (e.g., [Reference Braun, Greb, Langlois and MoragaBGL+, Exam.7.1]); in other words,
![]() $K_Y$
need not be
$K_Y$
need not be
![]() $\mathbb {Q}$
-Cartier.
$\mathbb {Q}$
-Cartier.
6.2.1 The stable locus
Now, let
![]() be the stable locus, and to fix notation, we have the map
be the stable locus, and to fix notation, we have the map
Note that since X is smooth, the Luna Slice Theorem implies that
![]() $Y^s$
is étale locally the quotient of a smooth variety U by some finite group
$Y^s$
is étale locally the quotient of a smooth variety U by some finite group
![]() $G_i$
. In particular,
$G_i$
. In particular,
![]() $Y^s$
is
$Y^s$
is
![]() $\mathbb {Q}$
-factorial, and there is a well-defined pullback
$\mathbb {Q}$
-factorial, and there is a well-defined pullback
![]() $q^{s*}$
for
$q^{s*}$
for
![]() $\mathbb {Q}$
-Weil divisor classes.
$\mathbb {Q}$
-Weil divisor classes.
In this situation, we have the following Riemann–Hurwitz lemma.
Lemma 6.1 (Riemann–Hurwitz for the stable locus).
Let
![]() $R^s$
be the divisorial locus in
$R^s$
be the divisorial locus in
![]() $X^s$
that has a stabilizer strictly containing
$X^s$
that has a stabilizer strictly containing
![]() $G_X$
(i.e., the union of codimension
$G_X$
(i.e., the union of codimension
![]() $1$
irreducible components of the locus of points in
$1$
irreducible components of the locus of points in
![]() $X^s$
where the stabilizer is not isomorphic to
$X^s$
where the stabilizer is not isomorphic to
![]() $G_X$
), let
$G_X$
), let
![]() $R^s=\bigcup R_i^s$
be its decomposition into irreducible components, and let
$R^s=\bigcup R_i^s$
be its decomposition into irreducible components, and let
![]() $G_{R_i}$
be the stabilizer of a general point of
$G_{R_i}$
be the stabilizer of a general point of
![]() $R_i^s$
. Then
$R_i^s$
. Then
Proof. It suffices to check étale locally. The Luna Slice Theorem implies that, up to a smooth factor, the quotient
![]() $q^s:X^s\to Y^s$
is étale locally equivalent to the quotient
$q^s:X^s\to Y^s$
is étale locally equivalent to the quotient
![]() $U\to U/G_i$
for a smooth scheme U and some finite group
$U\to U/G_i$
for a smooth scheme U and some finite group
![]() $G_i$
. Computing the canonical bundles is then a standard computation for the ramified cover
$G_i$
. Computing the canonical bundles is then a standard computation for the ramified cover
![]() $U\to U/G_i$
(see, e.g., [Reference Kollár and MoriKo
Reference Alexeev2, pp. 63–64]).
$U\to U/G_i$
(see, e.g., [Reference Kollár and MoriKo
Reference Alexeev2, pp. 63–64]).
6.2.2 Strictly semi-stable locus of codimension at least
 $2$
$2$
The computations for the stable locus carry over immediately to the general case, as long as the strictly semi-stable locus is of codimension at least
![]() $2$
. From now on, we will thus assume that
$2$
. From now on, we will thus assume that
![]() $X^{ss}-X^{s} \subseteq X^{ss}$
and
$X^{ss}-X^{s} \subseteq X^{ss}$
and
![]() $Y-Y^s\subseteq Y$
are codimension at least
$Y-Y^s\subseteq Y$
are codimension at least
![]() $2$
. Under this assumption, one can define a pullback
$2$
. Under this assumption, one can define a pullback
![]() $q^*$
on
$q^*$
on
![]() $\mathbb {Q}$
-Weil divisor classes by restricting to the stable locus
$\mathbb {Q}$
-Weil divisor classes by restricting to the stable locus
![]() $Y^s$
(which, as noted above, is
$Y^s$
(which, as noted above, is
![]() $\mathbb {Q}$
-factorial), pulling back to
$\mathbb {Q}$
-factorial), pulling back to
![]() $X^s$
, and then extending over the boundary, which is assumed to be of codimension at least
$X^s$
, and then extending over the boundary, which is assumed to be of codimension at least
![]() $2$
. This immediately yields the following.
$2$
. This immediately yields the following.
Corollary 6.2 (Riemann–Hurwitz).
Assume that
![]() $X^{ss}-X^{s} \subseteq X^{ss}$
and
$X^{ss}-X^{s} \subseteq X^{ss}$
and
![]() $Y-Y^s\subseteq Y$
have codimension at least
$Y-Y^s\subseteq Y$
have codimension at least
![]() $2$
. Then the same conclusion as in Lemma 6.1 holds:
$2$
. Then the same conclusion as in Lemma 6.1 holds:
where
![]() $R_i$
is the closure of
$R_i$
is the closure of
![]() $R_i^s$
in
$R_i^s$
in
![]() $X^{ss}$
.
$X^{ss}$
.
Remark 6.3. The codimension at least
![]() $2$
hypothesis above does rule out some standard GIT constructions. For instance, Corollary 6.2 is not applicable in the case of the GIT moduli space of cubic curves
$2$
hypothesis above does rule out some standard GIT constructions. For instance, Corollary 6.2 is not applicable in the case of the GIT moduli space of cubic curves
![]() ${\mathcal {M}}^{\operatorname {GIT}}_{\operatorname {curve}}$
, as the locus of strictly semi-stable cubic curves is the locus of
${\mathcal {M}}^{\operatorname {GIT}}_{\operatorname {curve}}$
, as the locus of strictly semi-stable cubic curves is the locus of
![]() $A_1$
cubic curves, which is a codimension
$A_1$
cubic curves, which is a codimension
![]() $1$
locus in the semi-stable locus in the Hilbert scheme
$1$
locus in the semi-stable locus in the Hilbert scheme
![]() $\mathbb {P}^{9}=\mathbb {P} H^0(\mathbb {P}^2,\mathcal {O}_{\mathbb {P}^2}(3))$
. Of course,
$\mathbb {P}^{9}=\mathbb {P} H^0(\mathbb {P}^2,\mathcal {O}_{\mathbb {P}^2}(3))$
. Of course,
![]() ${\mathcal {M}}^{\operatorname {GIT}}_{\operatorname {curve}}$
is simply equal to
${\mathcal {M}}^{\operatorname {GIT}}_{\operatorname {curve}}$
is simply equal to
![]() $\mathbb {P}^1$
, so this particular situation is trivial.
$\mathbb {P}^1$
, so this particular situation is trivial.
6.3 Canonical bundle of the Kirwan blowup
Here, we consider a step in the Kirwan blowup process:

We refer the reader to Kirwan’s various papers on the topic for the details on Kirwan blowups, or to our paper [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1] for a summary. For the convenience of the reader, recall that this includes the data of
![]() $\operatorname {Stab}^\circ \le G$
, a maximal dimensional connected component of a stabilizer, and the associated locus
$\operatorname {Stab}^\circ \le G$
, a maximal dimensional connected component of a stabilizer, and the associated locus
which is a smooth closed subvariety of
![]() $X^{ss}$
. Note that in Kirwan’s papers and in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1],
$X^{ss}$
. Note that in Kirwan’s papers and in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1],
![]() $\operatorname {Stab}^\circ $
is denoted by “R”; this would conflict with our notation here, that R is the Eckardt (ramification) divisor, and so we use the (possibly) more transparent
$\operatorname {Stab}^\circ $
is denoted by “R”; this would conflict with our notation here, that R is the Eckardt (ramification) divisor, and so we use the (possibly) more transparent
![]() $\operatorname {Stab}^\circ $
in the current paper.
$\operatorname {Stab}^\circ $
in the current paper.
Lemma 6.4. Assume that
![]() $X^{ss}-X^{s} \subseteq X^{ss}$
and
$X^{ss}-X^{s} \subseteq X^{ss}$
and
![]() $Y-Y^s\subseteq Y$
are codimension at least
$Y-Y^s\subseteq Y$
are codimension at least
![]() $2$
. Let
$2$
. Let
![]() $x\in Z_{\operatorname {Stab}^\circ }^{ss}$
be a general point, let
$x\in Z_{\operatorname {Stab}^\circ }^{ss}$
be a general point, let
![]() $\mathcal {N}_x$
be the fiber of the normal bundle to
$\mathcal {N}_x$
be the fiber of the normal bundle to
![]() $G\cdot Z_{\operatorname {Stab}^\circ }^{ss}$
in
$G\cdot Z_{\operatorname {Stab}^\circ }^{ss}$
in
![]() $X^{ss}$
at x, let
$X^{ss}$
at x, let
![]() $\ell _x\subseteq \mathcal {N}_x$
be a general line through the origin, and let
$\ell _x\subseteq \mathcal {N}_x$
be a general line through the origin, and let
![]() $c=\operatorname {codim}_X (G\cdot Z_{\operatorname {Stab}^\circ }^{ss})$
. Denote by
$c=\operatorname {codim}_X (G\cdot Z_{\operatorname {Stab}^\circ }^{ss})$
. Denote by
![]() $\widetilde R_i$
the strict transform of the ramification divisor
$\widetilde R_i$
the strict transform of the ramification divisor
![]() $R_i$
in
$R_i$
in
![]() $X^{ss}$
, denote by
$X^{ss}$
, denote by
![]() $G_{F}\subseteq G_x$
the stabilizer of the general line
$G_{F}\subseteq G_x$
the stabilizer of the general line
![]() $\ell _x$
, and denote by
$\ell _x$
, and denote by
![]() $\mu _i$
the coefficient defined by
$\mu _i$
the coefficient defined by
![]() $\tilde \pi ^* R_i=\widetilde R_i+\mu _i F$
. In terms of these invariants, the canonical bundles admit the following expressions:
$\tilde \pi ^* R_i=\widetilde R_i+\mu _i F$
. In terms of these invariants, the canonical bundles admit the following expressions:
 $$ \begin{align}\hspace{-12pt} K_{\widetilde Y}& = \pi ^*K_Y+\left(\frac{c+\sum (|G_{ R_i}|/|G_X| -1)\mu_i }{|G_F|/|G_X|}-1\right)E, \ \ \ \text{ if } Y \text{ is } \mathbb{Q}\text{-Gorenstein.} \end{align} $$
$$ \begin{align}\hspace{-12pt} K_{\widetilde Y}& = \pi ^*K_Y+\left(\frac{c+\sum (|G_{ R_i}|/|G_X| -1)\mu_i }{|G_F|/|G_X|}-1\right)E, \ \ \ \text{ if } Y \text{ is } \mathbb{Q}\text{-Gorenstein.} \end{align} $$
Proof. The first equality in (6.1) just follows from Corollary 6.2, using that F is the projectivized normal bundle to the orbit
![]() $G\cdot Z^{ss}_{\operatorname {Stab}^\circ }\subseteq X^{ss}$
, and the stabilizer of a generic point of F is therefore the stabilizer of the projectivized normal space at a generic point. The second equality in (6.1) is just the formula for the canonical bundle of the blowup of a smooth variety along a smooth subvariety.
$G\cdot Z^{ss}_{\operatorname {Stab}^\circ }\subseteq X^{ss}$
, and the stabilizer of a generic point of F is therefore the stabilizer of the projectivized normal space at a generic point. The second equality in (6.1) is just the formula for the canonical bundle of the blowup of a smooth variety along a smooth subvariety.
For (6.2), we use (6.1). Indeed, substituting the expressions
![]() $K_{\widetilde Y}= \pi ^*K_Y +a(E,Y,0)E$
and
$K_{\widetilde Y}= \pi ^*K_Y +a(E,Y,0)E$
and
![]() $K_{X^{ss}}= q^* K_Y+ \sum (|G_{ R_I}|/|G_X| -1)R_i$
, we obtain
$K_{X^{ss}}= q^* K_Y+ \sum (|G_{ R_I}|/|G_X| -1)R_i$
, we obtain
 $$ \begin{align*} K_{\widetilde X^{ss}}&= \tilde q^{*}\pi ^*K_{Y}+ a(E,Y,0)\left( |G_F|/|G_X| \right) F+\sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i + (|G_{F}|/|G_X| -1)F\\ &= \tilde q^{*} \pi ^*K_{Y}+ \sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i + \left((a(E,Y,0)+1)|G_{F}|/|G_X| -1\right)F,\\ K_{\widetilde X^{ss}}& = \tilde \pi^* q^*K_{Y} + \sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i +\sum (|G_{ R_i}|/|G_X| -1)\mu_i F+ (c-1) F \\ &= \tilde \pi^* q^*K_{Y} + \sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i + \left(c-1 +\sum (|G_{ R_i}|/|G_X| -1)\mu_i \right)F\,. \end{align*} $$
$$ \begin{align*} K_{\widetilde X^{ss}}&= \tilde q^{*}\pi ^*K_{Y}+ a(E,Y,0)\left( |G_F|/|G_X| \right) F+\sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i + (|G_{F}|/|G_X| -1)F\\ &= \tilde q^{*} \pi ^*K_{Y}+ \sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i + \left((a(E,Y,0)+1)|G_{F}|/|G_X| -1\right)F,\\ K_{\widetilde X^{ss}}& = \tilde \pi^* q^*K_{Y} + \sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i +\sum (|G_{ R_i}|/|G_X| -1)\mu_i F+ (c-1) F \\ &= \tilde \pi^* q^*K_{Y} + \sum (|G_{ R_i}|/|G_X| -1)\widetilde R_i + \left(c-1 +\sum (|G_{ R_i}|/|G_X| -1)\mu_i \right)F\,. \end{align*} $$
Solving for
![]() $a(E,Y,0)$
gives the result.
$a(E,Y,0)$
gives the result.
Remark 6.5. In order to effectively compute invariants on a Kirwan blowup (e.g., cohomology and canonical bundles), it is useful to be able to make computations directly on X, where one in principle has good control of the geometry and group action (as opposed to on the blowups of X). The invariants
![]() $\mu _i$
and
$\mu _i$
and
![]() $|G_F|$
in Lemma 6.4 are chosen for this reason; note that these can be computed at general points of the strata in X in Kirwan’s setup for the Kirwan blowup.
$|G_F|$
in Lemma 6.4 are chosen for this reason; note that these can be computed at general points of the strata in X in Kirwan’s setup for the Kirwan blowup.
Remark 6.6. From (6.2), one can see that
![]() $\mathbb {Q}$
-Gorenstein GIT quotients, in our restricted setup, have klt singularities. This is a special case of a much more general result due to Schoutens [Reference SchoutensS, Th. 2, p. 358]. We also note that one can conclude from this that certain moduli spaces of K-stable Fano manifolds are klt; this is again a special case of much deeper results of Braun et al. [Reference Braun, Greb, Langlois and MoragaBGL+] and [Reference Li, Wang and XuLWX].
$\mathbb {Q}$
-Gorenstein GIT quotients, in our restricted setup, have klt singularities. This is a special case of a much more general result due to Schoutens [Reference SchoutensS, Th. 2, p. 358]. We also note that one can conclude from this that certain moduli spaces of K-stable Fano manifolds are klt; this is again a special case of much deeper results of Braun et al. [Reference Braun, Greb, Langlois and MoragaBGL+] and [Reference Li, Wang and XuLWX].
Remark 6.7 (Kirwan blowups with boundary).
Still under the assumption that
![]() $X^{ss}-X^{s} \subseteq X^{ss}$
and
$X^{ss}-X^{s} \subseteq X^{ss}$
and
![]() $Y-Y^s\subseteq Y$
are codimension at least
$Y-Y^s\subseteq Y$
are codimension at least
![]() $2$
, if we consider the case of a boundary
$2$
, if we consider the case of a boundary
![]() $(Y,\Delta _Y)$
and assume that
$(Y,\Delta _Y)$
and assume that
![]() $K_Y+\Delta _Y$
is
$K_Y+\Delta _Y$
is
![]() $\mathbb {Q}$
-Cartier, then setting
$\mathbb {Q}$
-Cartier, then setting
![]() , and letting
, and letting
![]() $\Delta _{\widetilde Y}$
be the strict transform of
$\Delta _{\widetilde Y}$
be the strict transform of
![]() $\Delta _Y$
in
$\Delta _Y$
in
![]() $\widetilde Y$
, we have
$\widetilde Y$
, we have
 $$ \begin{align} K_{\widetilde Y}+\Delta_{\widetilde Y}& = \pi ^*(K_Y+\Delta_Y)+\left(\frac{a(F,X^{ss},\Delta_{X^{ss}})+1+\sum (|G_{ R_i}|/|G_X| -1)\mu_i }{|G_F|/|G_X|}-1\right)E\,. \end{align} $$
$$ \begin{align} K_{\widetilde Y}+\Delta_{\widetilde Y}& = \pi ^*(K_Y+\Delta_Y)+\left(\frac{a(F,X^{ss},\Delta_{X^{ss}})+1+\sum (|G_{ R_i}|/|G_X| -1)\mu_i }{|G_F|/|G_X|}-1\right)E\,. \end{align} $$
Indeed, setting
![]() $\Delta _{\widetilde X^{ss}}$
to be the strict transform of
$\Delta _{\widetilde X^{ss}}$
to be the strict transform of
![]() $\Delta _{X^{ss}}$
in
$\Delta _{X^{ss}}$
in
![]() $\widetilde X^{ss}$
, we have
$\widetilde X^{ss}$
, we have
![]() $\tilde q^*\Delta _{\widetilde Y}= \Delta _{\widetilde X^{ss}}$
; in our situation, both the strict transform and pullback are defined by restricting to the locus where the morphisms are either isomorphisms or étale, and then taking closures, and so the strict transform and pullback commute. Then the same analysis as above using
$\tilde q^*\Delta _{\widetilde Y}= \Delta _{\widetilde X^{ss}}$
; in our situation, both the strict transform and pullback are defined by restricting to the locus where the morphisms are either isomorphisms or étale, and then taking closures, and so the strict transform and pullback commute. Then the same analysis as above using
gives (6.3). Note that from (6.3), it follows that if
![]() $(X^{ss}, \Delta _{X^{ss}} = q^*\Delta _Y)$
is klt, then so is
$(X^{ss}, \Delta _{X^{ss}} = q^*\Delta _Y)$
is klt, then so is
![]() $(Y,\Delta _Y)$
; we emphasize that we started by assuming
$(Y,\Delta _Y)$
; we emphasize that we started by assuming
![]() $K_Y+\Delta _Y$
was
$K_Y+\Delta _Y$
was
![]() $\mathbb {Q}$
-Cartier.
$\mathbb {Q}$
-Cartier.
6.4 Computation of
 $K_{{\mathcal {M}}^{\operatorname {K}}}$
$K_{{\mathcal {M}}^{\operatorname {K}}}$
We now specialize the general discussion of the previous section to the particular case of the moduli of cubic surfaces. We want to apply Corollary 6.2 to compute
![]() $K_{{\mathcal {M}}^{\operatorname {GIT}}}$
, and then
$K_{{\mathcal {M}}^{\operatorname {GIT}}}$
, and then
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}$
. To do this for
$K_{{\mathcal {M}}^{\operatorname {K}}}$
. To do this for
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
, recall that the locus of unstable points in
${\mathcal {M}}^{\operatorname {GIT}}$
, recall that the locus of unstable points in
![]() $\mathbb {P}^{19}$
has codimension
$\mathbb {P}^{19}$
has codimension
![]() $\ge 2$
, and the locus of strictly semi-stable points has codimension
$\ge 2$
, and the locus of strictly semi-stable points has codimension
![]() $\ge 2$
in the semi-stable locus, both in
$\ge 2$
in the semi-stable locus, both in
![]() $(\mathbb {P}^{19})^{ss}$
as well as in
$(\mathbb {P}^{19})^{ss}$
as well as in
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
. Similarly, for
${\mathcal {M}}^{\operatorname {GIT}}$
. Similarly, for
![]() ${\mathcal {M}}^{\operatorname {K}}$
, the locus of unstable points in the blowup of
${\mathcal {M}}^{\operatorname {K}}$
, the locus of unstable points in the blowup of
![]() $(\mathbb {P}^{19})^{ss}$
has codimension
$(\mathbb {P}^{19})^{ss}$
has codimension
![]() $\ge 2$
, and the locus of strictly semi-stable points has codimension
$\ge 2$
, and the locus of strictly semi-stable points has codimension
![]() $\ge 2$
within the semi-stable locus, both in the blowup of
$\ge 2$
within the semi-stable locus, both in the blowup of
![]() $(\mathbb {P}^{19})^{ss}$
as well as in
$(\mathbb {P}^{19})^{ss}$
as well as in
![]() ${\mathcal {M}}^{\operatorname {K}}$
(see [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1]). We are thus in the setup of the previous section.
${\mathcal {M}}^{\operatorname {K}}$
(see [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1]). We are thus in the setup of the previous section.
Recall from §3 that the locus of cubics in
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
with nontrivial stabilizers is the irreducible Eckardt divisor R, and the cubic surface parameterized by a general point of R has automorphism group
${\mathcal {M}}^{\operatorname {GIT}}$
with nontrivial stabilizers is the irreducible Eckardt divisor R, and the cubic surface parameterized by a general point of R has automorphism group
![]() $\mathbb {Z}_2$
. Thus, the Riemann–Hurwitz formula (Corollary 6.2) in this case gives
$\mathbb {Z}_2$
. Thus, the Riemann–Hurwitz formula (Corollary 6.2) in this case gives
The class of the Eckardt divisor is known (see Remark 3.2).
![]() $R=\mathcal {O}_{\mathbb {P}^{19}}(100)$
, where
$R=\mathcal {O}_{\mathbb {P}^{19}}(100)$
, where
![]() $\mathcal {O}_{\mathbb {P}^{19}}(1)$
is the restriction to
$\mathcal {O}_{\mathbb {P}^{19}}(1)$
is the restriction to
![]() $(\mathbb {P}^{19})^{ss}$
of the hyperplane section in
$(\mathbb {P}^{19})^{ss}$
of the hyperplane section in
![]() $\mathbb {P}^{19}$
. Thus, we have
$\mathbb {P}^{19}$
. Thus, we have
giving
Recall also (e.g., Remark 3.2) that the discriminant has class
![]() $\mathcal {O}_{\mathbb {P}^{19}}(32)$
in our situation. In other words, as the discriminant in
$\mathcal {O}_{\mathbb {P}^{19}}(32)$
in our situation. In other words, as the discriminant in
![]() $(\mathbb {P}^{19})^{ss}$
descends to give the Weil divisor
$(\mathbb {P}^{19})^{ss}$
descends to give the Weil divisor
![]() $D_{A_1}$
on
$D_{A_1}$
on
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
, the divisor
${\mathcal {M}}^{\operatorname {GIT}}$
, the divisor
![]() $\mathcal {O}_{\mathbb {P}^{19}}(1)$
descends to
$\mathcal {O}_{\mathbb {P}^{19}}(1)$
descends to
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
(as a
${\mathcal {M}}^{\operatorname {GIT}}$
(as a
![]() $\mathbb {Q}$
-divisor) to give the
$\mathbb {Q}$
-divisor) to give the
![]() $\mathbb {Q}$
-Cartier divisor
$\mathbb {Q}$
-Cartier divisor
![]() $\frac {1}{32}D_{A_1}$
. This finally gives
$\frac {1}{32}D_{A_1}$
. This finally gives
agreeing with the computation in (3.10).
We now compute
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}$
using the same general machinery. Recall that the Kirwan desingularization for the case of cubic surfaces is obtained by a single blowup, supported at the point
$K_{{\mathcal {M}}^{\operatorname {K}}}$
using the same general machinery. Recall that the Kirwan desingularization for the case of cubic surfaces is obtained by a single blowup, supported at the point
![]() $\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
corresponding to the orbit of the
$\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
corresponding to the orbit of the
![]() $3A_2$
cubic surface
$3A_2$
cubic surface
![]() $S_{3A_2}$
.
$S_{3A_2}$
.
Corollary 6.8.
Proof. As discussed above, we are in a situation where we can employ Lemma 6.4 to compute the canonical bundle of
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}$
via the blowup of
$K_{{\mathcal {M}}^{\operatorname {K}}}$
via the blowup of
![]() $(\mathbb P^{19})^{ss}$
along the orbit of the
$(\mathbb P^{19})^{ss}$
along the orbit of the
![]() $3A_2$
cubic surface. The formula (6.2) of Lemma 6.4 states that
$3A_2$
cubic surface. The formula (6.2) of Lemma 6.4 states that
![]() $K_{{\mathcal {M}}^{\operatorname {K}}} = \pi ^* K_{{\mathcal {M}}^{\operatorname {GIT}}} +\left (\frac {c+|G_{R}|/|G_X| -1)\mu }{|G_{3A_2}|/|G_X|}-1\right )D_{3A_2}$
, where
$K_{{\mathcal {M}}^{\operatorname {K}}} = \pi ^* K_{{\mathcal {M}}^{\operatorname {GIT}}} +\left (\frac {c+|G_{R}|/|G_X| -1)\mu }{|G_{3A_2}|/|G_X|}-1\right )D_{3A_2}$
, where
![]() $G_X=\mu _4$
is the stabilizer of a general point of
$G_X=\mu _4$
is the stabilizer of a general point of
![]() $\mathbb P^{19}$
,
$\mathbb P^{19}$
,
![]() $G_R$
is the stabilizer of a general point of the Eckardt divisor,
$G_R$
is the stabilizer of a general point of the Eckardt divisor,
![]() $G_{3A_2}$
is the stabilizer of a general point of the exceptional divisor, c is the codimension of the
$G_{3A_2}$
is the stabilizer of a general point of the exceptional divisor, c is the codimension of the
![]() $3A_2$
orbit, and
$3A_2$
orbit, and
![]() $\mu $
is the multiplicity of the Eckardt locus along the
$\mu $
is the multiplicity of the Eckardt locus along the
![]() $3A_2$
orbit in the sense of Lemma 6.4. As a general Eckardt cubic surface has a
$3A_2$
orbit in the sense of Lemma 6.4. As a general Eckardt cubic surface has a
![]() $\mathbb Z_2$
automorphism group, we have that
$\mathbb Z_2$
automorphism group, we have that
![]() $|G_{R}|/|G_X|=2$
. Proposition 3.7(1) states that
$|G_{R}|/|G_X|=2$
. Proposition 3.7(1) states that
![]() $G_{3A2}=G_X=\mu _4$
. In other words, we have
$G_{3A2}=G_X=\mu _4$
. In other words, we have
![]() $K_{{\mathcal {M}}^{\operatorname {K}}} = \pi ^* K_{{\mathcal {M}}^{\operatorname {GIT}}} +(c+\mu -1)D_{3A_2}$
. Since we also have
$K_{{\mathcal {M}}^{\operatorname {K}}} = \pi ^* K_{{\mathcal {M}}^{\operatorname {GIT}}} +(c+\mu -1)D_{3A_2}$
. Since we also have
![]() $c=6$
(e.g., Lemma 3.4) and
$c=6$
(e.g., Lemma 3.4) and
![]() $\mu =15$
by Lemma 3.5, the result follows.
$\mu =15$
by Lemma 3.5, the result follows.
Remark 6.9. The coefficient
![]() $20$
for
$20$
for
![]() $D_{3A_2}$
(or at least the fact that the coefficient is divisible by
$D_{3A_2}$
(or at least the fact that the coefficient is divisible by
![]() $5$
) is crucial for our computation and proof of non-K-equivalence. Note that it follows immediately that while
$5$
) is crucial for our computation and proof of non-K-equivalence. Note that it follows immediately that while
![]() $\pi :{\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
is a blowup supported at the smooth point
$\pi :{\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
is a blowup supported at the smooth point
![]() $\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
, it is not the standard blowup of the point, since otherwise
$\Delta _{3A_2}\in {\mathcal {M}}^{\operatorname {GIT}}$
, it is not the standard blowup of the point, since otherwise
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}$
would equal
$K_{{\mathcal {M}}^{\operatorname {K}}}$
would equal
![]() $\pi ^*K_{{\mathcal {M}}^{\operatorname {GIT}}}+3D_{3A_2}$
.
$\pi ^*K_{{\mathcal {M}}^{\operatorname {GIT}}}+3D_{3A_2}$
.
6.5 Intersection numbers for divisors on DM stacks
On DM stacks, the top self-intersection numbers of canonical classes are rational numbers. We need the following statement regarding the denominators that may appear, which is essentially [Reference AlexeevAGV, Prop. 2.1.1].
Proposition 6.10. Let
![]() $\mathcal {X}$
be a smooth proper DM stack over a field K of characteristic
$\mathcal {X}$
be a smooth proper DM stack over a field K of characteristic
![]() $0$
with coarse moduli space
$0$
with coarse moduli space
![]() $\Phi :\mathcal {X}\to X$
of dimension d. For each geometric point
$\Phi :\mathcal {X}\to X$
of dimension d. For each geometric point
![]() ${p:\operatorname {Spec} \overline K \to \mathcal {X}}$
, denote by
${p:\operatorname {Spec} \overline K \to \mathcal {X}}$
, denote by
![]() $e_p$
the exponent of the automorphism group of p, and denote by e the least common multiple of the numbers
$e_p$
the exponent of the automorphism group of p, and denote by e the least common multiple of the numbers
![]() $e_p$
for all geometric points of
$e_p$
for all geometric points of
![]() $\mathcal {X}$
. For any divisor classes
$\mathcal {X}$
. For any divisor classes
![]() $D_1,\dots ,D_d\in \operatorname {CH}_{d-1}(X)$
, we have
$D_1,\dots ,D_d\in \operatorname {CH}_{d-1}(X)$
, we have
Proof. We first recall that for line bundles
![]() $M_1,\dots ,M_d$
on X, with divisor classes
$M_1,\dots ,M_d$
on X, with divisor classes
![]() $[M_1], \dots , [M_d]\in \operatorname {CH}_{d-1}(X)$
, we have by definition
$[M_1], \dots , [M_d]\in \operatorname {CH}_{d-1}(X)$
, we have by definition

Using the fact that X is
![]() $\mathbb {Q}$
-factorial, this allows us to define the intersection number
$\mathbb {Q}$
-factorial, this allows us to define the intersection number
![]() $D_1\cdots D_d$
as a rational number for any divisor classes
$D_1\cdots D_d$
as a rational number for any divisor classes
![]() $D_1,\dots ,D_d\in \operatorname {CH}_{d-1}(X)$
.
$D_1,\dots ,D_d\in \operatorname {CH}_{d-1}(X)$
.
To prove the bound on the denominators, we argue as follows. For any divisor
![]() $D\in \operatorname {CH}_{d-1}(X)$
, the pullback
$D\in \operatorname {CH}_{d-1}(X)$
, the pullback
![]() $\Phi ^*D$
is the divisor class associated with some line bundle
$\Phi ^*D$
is the divisor class associated with some line bundle
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $\mathcal {X}$
(given an étale presentation
$\mathcal {X}$
(given an étale presentation
![]() $P:U\to \mathcal {X}$
, the pullback
$P:U\to \mathcal {X}$
, the pullback
![]() $P^* \Phi ^*D$
is the class of a line bundle on U, which descends to
$P^* \Phi ^*D$
is the class of a line bundle on U, which descends to
![]() $\mathcal {X}$
). The fact that
$\mathcal {X}$
). The fact that
![]() $\mathcal {L}^{\otimes e}$
descends to a line bundle M on X is [Reference AlexeevAGV, Lem. 2.1.2]. Thus, we have
$\mathcal {L}^{\otimes e}$
descends to a line bundle M on X is [Reference AlexeevAGV, Lem. 2.1.2]. Thus, we have
![]() $(eD_1) \cdots (e D_d) \in \mathbb {Z}$
, completing the proof.
$(eD_1) \cdots (e D_d) \in \mathbb {Z}$
, completing the proof.
7 Proof of the non-K-equivalence
We can now conclude that
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are not K-equivalent, which is one of our main results. All the work for this proof has been already done, and we just gather the pieces here. We recall that the top self-intersection numbers of the canonical class on K-equivalent varieties are equal—this follows from say [Reference KollárKo
Reference Abramovich, Graber and Vistoli1, Chap. IV, App., Prop. 2.11, p. 296], which implies that if
${\overline {\mathcal {B}_4/\Gamma }}$
are not K-equivalent, which is one of our main results. All the work for this proof has been already done, and we just gather the pieces here. We recall that the top self-intersection numbers of the canonical class on K-equivalent varieties are equal—this follows from say [Reference KollárKo
Reference Abramovich, Graber and Vistoli1, Chap. IV, App., Prop. 2.11, p. 296], which implies that if
![]() $f:Y\to X$
is a morphism of schemes of dimension d over a field, such that
$f:Y\to X$
is a morphism of schemes of dimension d over a field, such that
![]() $f_*(\mathcal {O}_Y) = \mathcal {O}_X$
, and
$f_*(\mathcal {O}_Y) = \mathcal {O}_X$
, and
![]() $D_i$
are
$D_i$
are
![]() $\mathbb {Q}$
-Cartier divisors on X, then
$\mathbb {Q}$
-Cartier divisors on X, then
![]() $f^*D_1\cdots f^*D_d = D_1\cdots D_d$
. Consequently, given two K-equivalent birational normal projective
$f^*D_1\cdots f^*D_d = D_1\cdots D_d$
. Consequently, given two K-equivalent birational normal projective
![]() $\mathbb {Q}$
-Gorenstein varieties X and Y of dimension d, one has from the definition of K-equivalence that, in the notation of diagram (1.1),
$\mathbb {Q}$
-Gorenstein varieties X and Y of dimension d, one has from the definition of K-equivalence that, in the notation of diagram (1.1),
![]() $K_X^d=g^*K_X^d= K_Z^d=h^*K_Y^d=K_Y^d$
.
$K_X^d=g^*K_X^d= K_Z^d=h^*K_Y^d=K_Y^d$
.
We will thus prove Theorem 1.2 by showing that the top self-intersection numbers of the canonical classes on the Kirwan and toroidal compactifications are not equal to each other. Showing that the top self-intersection numbers of
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}$
and of
$K_{{\mathcal {M}}^{\operatorname {K}}}$
and of
![]() $K_{{\overline {\mathcal {B}_4/\Gamma }}}$
are not equal to each other is greatly simplified by the fact that both of these spaces admit blowdown maps (
$K_{{\overline {\mathcal {B}_4/\Gamma }}}$
are not equal to each other is greatly simplified by the fact that both of these spaces admit blowdown maps (
![]() $\pi $
and p, respectively) to the same space
$\pi $
and p, respectively) to the same space
![]() ${(\mathcal {B}_4/\Gamma )^*}={\mathcal {M}}^{\operatorname {GIT}}$
, with the exceptional divisors of
${(\mathcal {B}_4/\Gamma )^*}={\mathcal {M}}^{\operatorname {GIT}}$
, with the exceptional divisors of
![]() $\pi $
and p both contracted to a single point
$\pi $
and p both contracted to a single point
![]() $\Delta _{3A_2}$
. Thus, as computed above, the canonical class in each case is the pullback of the canonical bundle
$\Delta _{3A_2}$
. Thus, as computed above, the canonical class in each case is the pullback of the canonical bundle
![]() $K_{{\mathcal {M}}^{\operatorname {GIT}}}$
plus the exceptional divisor of the blowup with a suitable multiplicity. Since the exceptional divisors of
$K_{{\mathcal {M}}^{\operatorname {GIT}}}$
plus the exceptional divisor of the blowup with a suitable multiplicity. Since the exceptional divisors of
![]() $\pi $
and p are both contracted to a point, the top self-intersection numbers of
$\pi $
and p are both contracted to a point, the top self-intersection numbers of
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}$
and
$K_{{\mathcal {M}}^{\operatorname {K}}}$
and
![]() $K_{{\overline {\mathcal {B}_4/\Gamma }}}$
will each equal to the top self-intersection number of
$K_{{\overline {\mathcal {B}_4/\Gamma }}}$
will each equal to the top self-intersection number of
![]() $K_{{\mathcal {M}}^{\operatorname {GIT}}}$
plus a suitable multiple of the top self-intersection number of the corresponding exceptional divisor.
$K_{{\mathcal {M}}^{\operatorname {GIT}}}$
plus a suitable multiple of the top self-intersection number of the corresponding exceptional divisor.
Proof of Theorem 1.2
By the above discussion, it suffices to show that
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}^4\ne K_{{\overline {\mathcal {B}_4/\Gamma }}}^4$
. To this end, recall from Corollary 6.8 and Proposition 5.8 that
$K_{{\mathcal {M}}^{\operatorname {K}}}^4\ne K_{{\overline {\mathcal {B}_4/\Gamma }}}^4$
. To this end, recall from Corollary 6.8 and Proposition 5.8 that
 $$ \begin{align*} K_{{\mathcal {M}}^{\operatorname{K}}}& = \pi ^* K_{ {\mathcal {M}}^{\operatorname{GIT}}}+20D_{3A2}\,,\\ K_{{\overline{\mathcal {B}_4/\Gamma }}} & = p^* K_{{\mathcal {M}}^{\operatorname{GIT}}}+16T_{3A_2}\,. \end{align*} $$
$$ \begin{align*} K_{{\mathcal {M}}^{\operatorname{K}}}& = \pi ^* K_{ {\mathcal {M}}^{\operatorname{GIT}}}+20D_{3A2}\,,\\ K_{{\overline{\mathcal {B}_4/\Gamma }}} & = p^* K_{{\mathcal {M}}^{\operatorname{GIT}}}+16T_{3A_2}\,. \end{align*} $$
The top self-intersection number for the latter is then
by Lemma 5.11. We then compute
By Proposition 6.10 we have
![]() $D_{3A_2}^4\in \frac {1}{e}\mathbb {Z}$
for some e that is not divisible by
$D_{3A_2}^4\in \frac {1}{e}\mathbb {Z}$
for some e that is not divisible by
![]() $5$
; indeed,
$5$
; indeed,
![]() $D_{3A_2}^4= (D_{3A_2}|_{D_{3A_2}})^3$
, where we are using that
$D_{3A_2}^4= (D_{3A_2}|_{D_{3A_2}})^3$
, where we are using that
![]() ${\mathcal {M}}^{\operatorname {K}}$
is
${\mathcal {M}}^{\operatorname {K}}$
is
![]() $\mathbb {Q}$
-factorial to define the restriction. By Proposition 3.7, no stabilizers along
$\mathbb {Q}$
-factorial to define the restriction. By Proposition 3.7, no stabilizers along
![]() $D_{3A_2}$
have order divisible by
$D_{3A_2}$
have order divisible by
![]() $5$
. Consequently, the two intersection numbers
$5$
. Consequently, the two intersection numbers
![]() $K_{{\mathcal {M}}^{\operatorname {K}}}^4$
and
$K_{{\mathcal {M}}^{\operatorname {K}}}^4$
and
![]() $K_{{\overline {\mathcal {B}_4/\Gamma }}}^4$
cannot be the same since if we write
$K_{{\overline {\mathcal {B}_4/\Gamma }}}^4$
cannot be the same since if we write
![]() $5^42^8D_{3A_2}^4$
as a product of nonzero powers of distinct primes,
$5^42^8D_{3A_2}^4$
as a product of nonzero powers of distinct primes,
![]() $5$
will appear with positive exponent, while it does not appear with positive exponent in
$5$
will appear with positive exponent, while it does not appear with positive exponent in
![]() $-\tfrac {16^4}{6^3}=-\tfrac {2^{13}}{3^3}$
.
$-\tfrac {16^4}{6^3}=-\tfrac {2^{13}}{3^3}$
.
8 Proof of equality in the Grothendieck ring of varieties
In this section, we show that
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
have the same class in the Grothendieck ring of varieties, which is our last main result to be proven. Due to the fact that moduli spaces of cubic surfaces have no odd degree cohomology, this will turn out to give another, conceptual rather than computational, proof that these two compactifications have the same cohomology (Corollary 8.5).
${\overline {\mathcal {B}_4/\Gamma }}$
have the same class in the Grothendieck ring of varieties, which is our last main result to be proven. Due to the fact that moduli spaces of cubic surfaces have no odd degree cohomology, this will turn out to give another, conceptual rather than computational, proof that these two compactifications have the same cohomology (Corollary 8.5).
Proof of Theorem 1.3
Since
![]() ${\mathcal {M}}^{\operatorname {K}}- D_{3A_2}\cong {\overline {\mathcal {B}_4/\Gamma }}- T_{3A_2}$
, by additivity of the class of the disjoint union of varieties in the Grothendieck ring, it suffices to show that the exceptional divisors
${\mathcal {M}}^{\operatorname {K}}- D_{3A_2}\cong {\overline {\mathcal {B}_4/\Gamma }}- T_{3A_2}$
, by additivity of the class of the disjoint union of varieties in the Grothendieck ring, it suffices to show that the exceptional divisors
![]() $D_{3A_2}$
and
$D_{3A_2}$
and
![]() $T_{3A_2}$
, as varieties, are equivalent in the Grothendieck ring. Since we have seen that
$T_{3A_2}$
, as varieties, are equivalent in the Grothendieck ring. Since we have seen that
![]() $T_{3A_2}$
is isomorphic to
$T_{3A_2}$
is isomorphic to
![]() $\mathbb {P}^3$
, it thus suffices to show that
$\mathbb {P}^3$
, it thus suffices to show that
![]() $D_{3A_2}$
is equivalent to
$D_{3A_2}$
is equivalent to
![]() $\mathbb {P}^3$
in the Grothendieck ring. This is accomplished below in Lemma 8.1 (for an alternative approach and proof, see Lemma 8.2 and Remark 8.4).
$\mathbb {P}^3$
in the Grothendieck ring. This is accomplished below in Lemma 8.1 (for an alternative approach and proof, see Lemma 8.2 and Remark 8.4).
We now describe explicitly the geometry of the exceptional divisor
![]() $D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
, by thinking of it as the GIT quotient of the exceptional divisor
$D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
, by thinking of it as the GIT quotient of the exceptional divisor
![]() $\mathbb {P}^5$
of the blowup of the Luna slice by the group
$\mathbb {P}^5$
of the blowup of the Luna slice by the group
![]() $\operatorname {Aut}(S_{3A_2})$
. Recall that
$\operatorname {Aut}(S_{3A_2})$
. Recall that
![]() $\operatorname {Aut}(S_{3A_2})$
is the semidirect product of
$\operatorname {Aut}(S_{3A_2})$
is the semidirect product of
![]() $\mathbb {T}^2$
and
$\mathbb {T}^2$
and
![]() $S_3$
, as described in Lemma 3.3. Furthermore, the
$S_3$
, as described in Lemma 3.3. Furthermore, the
![]() $\mathbb {C}^6$
Luna slice is described in Lemma 3.4, and the action of
$\mathbb {C}^6$
Luna slice is described in Lemma 3.4, and the action of
![]() $\operatorname {Aut}(S_{3A_2})$
on it is given by (3.18). We are interested in the action of
$\operatorname {Aut}(S_{3A_2})$
on it is given by (3.18). We are interested in the action of
![]() $\operatorname {Aut}(S_{3A_2})$
on the exceptional divisor of the blowup
$\operatorname {Aut}(S_{3A_2})$
on the exceptional divisor of the blowup
![]() $\operatorname {Bl}_0\mathbb {C}^6\to \mathbb {C}^6$
of the Luna slice at the origin. Recall that the action of
$\operatorname {Bl}_0\mathbb {C}^6\to \mathbb {C}^6$
of the Luna slice at the origin. Recall that the action of
![]() $S_3$
on the exceptional
$S_3$
on the exceptional
![]() $\mathbb {P}^5$
is simply by permuting the homogeneous coordinates
$\mathbb {P}^5$
is simply by permuting the homogeneous coordinates
![]() $(T_0:T_1:T_2:T_{\widehat 0}:T_{\widehat 1}:T_{\widehat 2})$
pairwise. Our goal is to describe all semi-stable orbits, up to the action of
$(T_0:T_1:T_2:T_{\widehat 0}:T_{\widehat 1}:T_{\widehat 2})$
pairwise. Our goal is to describe all semi-stable orbits, up to the action of
![]() $S_3$
. Recall that the set of unstable orbits has already been determined in Lemma 3.6.
$S_3$
. Recall that the set of unstable orbits has already been determined in Lemma 3.6.
We will describe sets of various orbits of the same type, where by type we will simply mean which of the homogeneous coordinates T vanish (and we will write
![]() $0$
for them), and which of the coordinates T do not vanish (and we will write
$0$
for them), and which of the coordinates T do not vanish (and we will write
![]() $*$
for an arbitrary nonzero complex number). For such a given type of an orbit, we will parameterize the orbits of such a type by a number of copies of
$*$
for an arbitrary nonzero complex number). For such a given type of an orbit, we will parameterize the orbits of such a type by a number of copies of
![]() $\mathbb {C}^*$
, for the nonzero coordinates, quotiented by a finite group. Indeed, for all orbits of a given type, we can set one of the nonzero (labeled
$\mathbb {C}^*$
, for the nonzero coordinates, quotiented by a finite group. Indeed, for all orbits of a given type, we can set one of the nonzero (labeled
![]() $*$
) homogeneous coordinates T to be equal to 1 by projectivizing, and then set two more of the nonzero homogeneous coordinates to be equal to 1 by acting by
$*$
) homogeneous coordinates T to be equal to 1 by projectivizing, and then set two more of the nonzero homogeneous coordinates to be equal to 1 by acting by
![]() $\mathbb {T}^2\subseteq \operatorname {Aut}(S_{3A_2})$
. However, a given
$\mathbb {T}^2\subseteq \operatorname {Aut}(S_{3A_2})$
. However, a given
![]() $\mathbb {T}^2$
orbit may contain more than one point where these three chosen coordinates are equal to 1, due to finite stabilizers that we will describe in detail in Lemma 8.1.
$\mathbb {T}^2$
orbit may contain more than one point where these three chosen coordinates are equal to 1, due to finite stabilizers that we will describe in detail in Lemma 8.1.
To enumerate possible types of orbits, up to the
![]() $S_3$
action, we will always permute the coordinates
$S_3$
action, we will always permute the coordinates
![]() $T_0,T_1,T_2$
in such a way that all zeros precede all nonzero coordinates. If possible to do so while keeping this condition for
$T_0,T_1,T_2$
in such a way that all zeros precede all nonzero coordinates. If possible to do so while keeping this condition for
![]() $T_0,T_1,T_2$
, we will further permute
$T_0,T_1,T_2$
, we will further permute
![]() $T_{\widehat 0},T_{\widehat 1},T_{\widehat 2}$
to also put all zeros before all the nonzero coordinates. Recalling from Lemma 3.6 that semi-stable points on
$T_{\widehat 0},T_{\widehat 1},T_{\widehat 2}$
to also put all zeros before all the nonzero coordinates. Recalling from Lemma 3.6 that semi-stable points on
![]() $\mathbb {P}^5$
are those where
$\mathbb {P}^5$
are those where
![]() $T_i\ne 0$
or
$T_i\ne 0$
or
![]() $T_{\widehat {i}}\ne 0$
, for each
$T_{\widehat {i}}\ne 0$
, for each
![]() $i=0,1,2$
, we thus enumerate the types of semi-stable (in fact all of them stable)
$i=0,1,2$
, we thus enumerate the types of semi-stable (in fact all of them stable)
![]() $\mathbb {T}^2$
orbits on
$\mathbb {T}^2$
orbits on
![]() $\mathbb {P}^5$
, and their contributions to the class
$\mathbb {P}^5$
, and their contributions to the class
![]() $[D_{3A_2}]$
in the Grothendieck ring of varieties in Table 1 (where we number the types of orbits, for easy reference).
$[D_{3A_2}]$
in the Grothendieck ring of varieties in Table 1 (where we number the types of orbits, for easy reference).
Table 1 Stable
![]() $\mathbb {T}^2$
orbits on
$\mathbb {T}^2$
orbits on
![]() $\mathbb {P}^5$
$\mathbb {P}^5$

Here, we note that the quotient of
![]() $\mathbb {C}^*$
by any finite subgroup is still a
$\mathbb {C}^*$
by any finite subgroup is still a
![]() $\mathbb {C}^*$
, so that contributions from (4) and (6) are equal to
$\mathbb {C}^*$
, so that contributions from (4) and (6) are equal to
![]() $[\mathbb {C}^*]$
. Thus, to compute the class of
$[\mathbb {C}^*]$
. Thus, to compute the class of
![]() $D_{3A_2}$
in the Grothendieck ring of varieties, it remains to compute the classes of the higher-dimensional quotients, for which we need to understand the actions of
$D_{3A_2}$
in the Grothendieck ring of varieties, it remains to compute the classes of the higher-dimensional quotients, for which we need to understand the actions of
![]() $S_2$
and
$S_2$
and
![]() $S_3$
appearing in the orbits of types (1)–(3) above.
$S_3$
appearing in the orbits of types (1)–(3) above.
Lemma 8.1. The divisor
![]() $D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
is equivalent to
$D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
is equivalent to
![]() $\mathbb {P}^3$
in the Grothendieck ring of varieties.
$\mathbb {P}^3$
in the Grothendieck ring of varieties.
Proof. From the table of contributions (Table 1), and referring to the types of orbits by those numbers, we compute the class in the Grothendieck ring to be
where the first three summands denote the classes in the Grothendieck ring of varieties of the orbits of the corresponding types from Table 1. We start with locus (1), noticing first that any
![]() $\mathbb {T}^2$
orbit of any such point contains a point whose homogeneous coordinates are
$\mathbb {T}^2$
orbit of any such point contains a point whose homogeneous coordinates are
![]() $(*:*:*:1:1:1)$
(i.e., such that
$(*:*:*:1:1:1)$
(i.e., such that
![]() $T_{\widehat 0}=T_{\widehat 1}=T_{\widehat 2}=1$
). Moreover, looking at the explicit action of
$T_{\widehat 0}=T_{\widehat 1}=T_{\widehat 2}=1$
). Moreover, looking at the explicit action of
![]() $\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2)\in D"\simeq \mathbb {T}^2$
(with
$\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2)\in D"\simeq \mathbb {T}^2$
(with
![]() $\lambda _0\lambda _1\lambda _2=1$
) given by (3.20), if
$\lambda _0\lambda _1\lambda _2=1$
) given by (3.20), if
![]() $(T_0:T_1:T_2:1:1:1)$
and
$(T_0:T_1:T_2:1:1:1)$
and
![]() $(T^{\prime }_0:T^{\prime }_1:T^{\prime }_2:1:1:1)$
lie on the same
$(T^{\prime }_0:T^{\prime }_1:T^{\prime }_2:1:1:1)$
lie on the same
![]() $\mathbb {T}^2$
orbit, it means that there must exist
$\mathbb {T}^2$
orbit, it means that there must exist
![]() $(\lambda _0,\lambda _1,\lambda _2)\in \mathbb {T}^2$
such that
$(\lambda _0,\lambda _1,\lambda _2)\in \mathbb {T}^2$
such that
![]() $\lambda _0^2=\lambda _1^2=\lambda _2^2$
and such that
$\lambda _0^2=\lambda _1^2=\lambda _2^2$
and such that
![]() $T_i=\lambda _i^3 T^{\prime }_i$
for
$T_i=\lambda _i^3 T^{\prime }_i$
for
![]() $i=0,1,2$
. This means that each of the three
$i=0,1,2$
. This means that each of the three
![]() $\lambda _i$
must be equal to some
$\lambda _i$
must be equal to some
![]() $\sigma _i=\pm 1$
, subject to the condition that the product of the three signs is equal to
$\sigma _i=\pm 1$
, subject to the condition that the product of the three signs is equal to
![]() $+1$
, and the values of
$+1$
, and the values of
![]() $T_i$
and
$T_i$
and
![]() $T_i'$
must then differ by the corresponding signs. Thus, the set of orbits of this form is equal to
$T_i'$
must then differ by the corresponding signs. Thus, the set of orbits of this form is equal to
where G is the subgroup of
![]() $\mu _2\times \mu _2\times \mu _2$
given by the condition
$\mu _2\times \mu _2\times \mu _2$
given by the condition
![]() $\sigma _0\sigma _1\sigma _2=1$
, and the action is by diagonal multiplication. The action of
$\sigma _0\sigma _1\sigma _2=1$
, and the action is by diagonal multiplication. The action of
![]() $S_3$
on
$S_3$
on
![]() $(\mathbb {C}^*)^3/G$
is induced by permuting the coordinates on
$(\mathbb {C}^*)^3/G$
is induced by permuting the coordinates on
![]() $(\mathbb {C}^*)^3$
, and we note that it does not commute with the action of G. For example, acting by signs
$(\mathbb {C}^*)^3$
, and we note that it does not commute with the action of G. For example, acting by signs
![]() $(-1,1,-1)$
maps
$(-1,1,-1)$
maps
![]() $T_0:T_1:T_2$
to
$T_0:T_1:T_2$
to
![]() $-T_0:T_1:-T_2$
, and then permuting
$-T_0:T_1:-T_2$
, and then permuting
![]() $0\leftrightarrow 1$
gives
$0\leftrightarrow 1$
gives
![]() $T_1:-T_0:-T_2$
, while first permuting and then acting by signs gives
$T_1:-T_0:-T_2$
, while first permuting and then acting by signs gives
![]() $-T_1:T_0:-T_2$
.
$-T_1:T_0:-T_2$
.
By taking the squares of the coordinates, we observe that the quotient
![]() $(\mathbb {C}^*)^3/(\mu _2\times \mu _2\times \mu _2)$
, where the action is by multiplication by three independent signs, is isomorphic to
$(\mathbb {C}^*)^3/(\mu _2\times \mu _2\times \mu _2)$
, where the action is by multiplication by three independent signs, is isomorphic to
![]() $(\mathbb {C}^*)^3$
. Furthermore, recall that the quotient
$(\mathbb {C}^*)^3$
. Furthermore, recall that the quotient
![]() $\mathbb {C}^3/S_3$
, under the action that permutes coordinates, is identified with
$\mathbb {C}^3/S_3$
, under the action that permutes coordinates, is identified with
![]() $\mathbb {C}^3$
by taking elementary symmetric polynomials, that is, the bijection
$\mathbb {C}^3$
by taking elementary symmetric polynomials, that is, the bijection
![]() $\mathbb {C}^3/S_3\simeq \mathbb {C}^3$
is given in coordinates by
$\mathbb {C}^3/S_3\simeq \mathbb {C}^3$
is given in coordinates by
By inspection, the image of
![]() $(\mathbb {C}^*)^3\subseteq \mathbb {C}^3$
under this bijection is
$(\mathbb {C}^*)^3\subseteq \mathbb {C}^3$
under this bijection is
![]() $\mathbb {C}^*\times \mathbb {C}^2\simeq (\mathbb {C}^*)^3/S_3$
. Altogether, this means that the map
$\mathbb {C}^*\times \mathbb {C}^2\simeq (\mathbb {C}^*)^3/S_3$
. Altogether, this means that the map
identifies the quotient
![]() $(\mathbb {C}^*)^3/(\mu _2^{\times 3})\rtimes S_3$
with
$(\mathbb {C}^*)^3/(\mu _2^{\times 3})\rtimes S_3$
with
![]() $\mathbb {C}^*\times \mathbb {C}^2$
. The contribution
$\mathbb {C}^*\times \mathbb {C}^2$
. The contribution
![]() $[(1)]$
to the class
$[(1)]$
to the class
![]() $[D_{3A_2}]$
is
$[D_{3A_2}]$
is
![]() $[(\mathbb {C}^*)^3/G\rtimes S_3]$
. We now claim that the double cover
$[(\mathbb {C}^*)^3/G\rtimes S_3]$
. We now claim that the double cover
is étale. Indeed, to prove this, we need to check that no element of
![]() $((\mu _2)^{\times 3}\rtimes S_3)- (G\rtimes S_3)$
stabilizes any point in the domain of this map. Indeed, up to renumbering the coordinates, we need to worry about the permutation being the identity, an involution
$((\mu _2)^{\times 3}\rtimes S_3)- (G\rtimes S_3)$
stabilizes any point in the domain of this map. Indeed, up to renumbering the coordinates, we need to worry about the permutation being the identity, an involution
![]() $0\leftrightarrow 1$
or the cycle
$0\leftrightarrow 1$
or the cycle
![]() $0\mapsto 1\mapsto 2\mapsto 0$
, and the signs can either all be minus, or just one sign can be minus. We thus check case by case that there are no fixed points:
$0\mapsto 1\mapsto 2\mapsto 0$
, and the signs can either all be minus, or just one sign can be minus. We thus check case by case that there are no fixed points:
 $$ \begin{align*}\begin{aligned} (T_0,T_1,T_2)&=(-T_0,T_1,T_2)&\Rightarrow T_0=0,\,\,\\ (T_0,T_1,T_2)&=(-T_0,-T_1,-T_2)&\Rightarrow T_0=T_1=T_2=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,T_0,T_2)&\Rightarrow T_0=-T_1=-T_0\Rightarrow T_0=T_1=0,\,\,\\ (T_0,T_1,T_2)&=(T_1,T_0,-T_2)&\Rightarrow T_2=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,-T_0,-T_2)&\Rightarrow T_2=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,T_2,T_0)&\Rightarrow T_0=-T_1=-T_2=-T_0\Rightarrow T_0=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,-T_2,-T_0)&\Rightarrow T_0=-T_1=T_2=-T_0\Rightarrow T_0=0\,,\\ \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} (T_0,T_1,T_2)&=(-T_0,T_1,T_2)&\Rightarrow T_0=0,\,\,\\ (T_0,T_1,T_2)&=(-T_0,-T_1,-T_2)&\Rightarrow T_0=T_1=T_2=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,T_0,T_2)&\Rightarrow T_0=-T_1=-T_0\Rightarrow T_0=T_1=0,\,\,\\ (T_0,T_1,T_2)&=(T_1,T_0,-T_2)&\Rightarrow T_2=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,-T_0,-T_2)&\Rightarrow T_2=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,T_2,T_0)&\Rightarrow T_0=-T_1=-T_2=-T_0\Rightarrow T_0=0,\,\,\\ (T_0,T_1,T_2)&=(-T_1,-T_2,-T_0)&\Rightarrow T_0=-T_1=T_2=-T_0\Rightarrow T_0=0\,,\\ \end{aligned} \end{align*} $$
so that in each case we deduce that some coordinate must be zero, and thus the fixed point set in
![]() $(\mathbb {C}^*)^3$
is empty. Since the only connected étale double cover of
$(\mathbb {C}^*)^3$
is empty. Since the only connected étale double cover of
![]() $\mathbb {C}^*\times \mathbb {C}^2$
is topologically itself (covering along the
$\mathbb {C}^*\times \mathbb {C}^2$
is topologically itself (covering along the
![]() $\mathbb {C}^*$
factor), it follows that
$\mathbb {C}^*$
factor), it follows that
![]() $[(1)]=[\mathbb {C}^*\times \mathbb {C}^2]$
in the Grothendieck ring.
$[(1)]=[\mathbb {C}^*\times \mathbb {C}^2]$
in the Grothendieck ring.
The contributions to the class in the Grothendieck ring of the orbits of types (2) and (3) are simpler. For (2), similarly to the previous case, we can always find a representative with homogeneous coordinates of the form
![]() $(T_0:T_1:0:1:1:1)$
, and such a point lies on the same
$(T_0:T_1:0:1:1:1)$
, and such a point lies on the same
![]() $\mathbb {T}^2$
orbit as
$\mathbb {T}^2$
orbit as
![]() $(T^{\prime }_0:T^{\prime }_1:0:1:1:1)$
if and only if
$(T^{\prime }_0:T^{\prime }_1:0:1:1:1)$
if and only if
![]() $T_0=\pm T^{\prime }_0$
and
$T_0=\pm T^{\prime }_0$
and
![]() $T_1=\pm T^{\prime }_1$
, with the signs chosen independently (as the signs can be compensated by choosing the suitable sign for
$T_1=\pm T^{\prime }_1$
, with the signs chosen independently (as the signs can be compensated by choosing the suitable sign for
![]() $\lambda _2$
, multiplying by which fixes the zero coordinate
$\lambda _2$
, multiplying by which fixes the zero coordinate
![]() $T_2$
anyway). Thus, the set of such orbits is
$T_2$
anyway). Thus, the set of such orbits is
![]() $(\mathbb {C}^*/\mu _2)^2\simeq (\mathbb {C}^*)^2$
, where the explicit isomorphism is given by squaring each coordinate. Then the action of the coordinate interchange involution
$(\mathbb {C}^*/\mu _2)^2\simeq (\mathbb {C}^*)^2$
, where the explicit isomorphism is given by squaring each coordinate. Then the action of the coordinate interchange involution
![]() $0\leftrightarrow 1$
in these coordinates, as an action on
$0\leftrightarrow 1$
in these coordinates, as an action on
![]() $(\mathbb {C}^*)^2$
, is simply the interchange of the two coordinates, that is, the restriction to
$(\mathbb {C}^*)^2$
, is simply the interchange of the two coordinates, that is, the restriction to
![]() $(\mathbb {C}^*)^2\subseteq \mathbb {C}^2$
of the usual action of
$(\mathbb {C}^*)^2\subseteq \mathbb {C}^2$
of the usual action of
![]() $S_2$
interchanging the two coordinates. Under the bijection
$S_2$
interchanging the two coordinates. Under the bijection
![]() $\mathbb {C}^2/S_2\leftrightarrow \mathbb {C}^2$
given explicitly by
$\mathbb {C}^2/S_2\leftrightarrow \mathbb {C}^2$
given explicitly by
the image of
![]() $(\mathbb {C}^*)^2$
is equal to
$(\mathbb {C}^*)^2$
is equal to
![]() $\mathbb {C}^*\times \mathbb {C}$
, and thus
$\mathbb {C}^*\times \mathbb {C}$
, and thus
![]() $[(2)]=[\mathbb {C}^*\times \mathbb {C}]$
.
$[(2)]=[\mathbb {C}^*\times \mathbb {C}]$
.
Finally, for orbits of type (3), each orbit has a representative of the form
![]() $(T_0:1:T_2:1:0:1)$
(we choose this form as it is preserved by the involution
$(T_0:1:T_2:1:0:1)$
(we choose this form as it is preserved by the involution
![]() $0\leftrightarrow 2$
), and such a point lies on the same
$0\leftrightarrow 2$
), and such a point lies on the same
![]() $\mathbb {T}^2$
orbit as
$\mathbb {T}^2$
orbit as
![]() $(T^{\prime }_0:1:T^{\prime }_2:1:0:1)$
if and only if they are mapped to each other by the action of
$(T^{\prime }_0:1:T^{\prime }_2:1:0:1)$
if and only if they are mapped to each other by the action of
![]() $\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2)$
, which means we must have
$\operatorname {diag}(\lambda _0,\lambda _1,\lambda _2)$
, which means we must have
![]() $\lambda _0\lambda _1\lambda _2=1$
and
$\lambda _0\lambda _1\lambda _2=1$
and
![]() $\lambda _0^2=\lambda _2^2=\lambda _1^3=1$
. This is to say
$\lambda _0^2=\lambda _2^2=\lambda _1^3=1$
. This is to say
![]() $\lambda _0=\lambda _2=\sigma =\pm 1$
and
$\lambda _0=\lambda _2=\sigma =\pm 1$
and
![]() $\lambda _1=1$
, and thus the set of such orbits is
$\lambda _1=1$
, and thus the set of such orbits is
![]() $(\mathbb {C}^*)^2/\mu _2$
, where the action is by multiplying both coordinates by
$(\mathbb {C}^*)^2/\mu _2$
, where the action is by multiplying both coordinates by
![]() $-1$
simultaneously. Similarly to orbits of type (2), this action of
$-1$
simultaneously. Similarly to orbits of type (2), this action of
![]() $\mu _2$
commutes with the action of the coordinate interchange involution, and thus the contribution to the Grothendieck ring of varieties is
$\mu _2$
commutes with the action of the coordinate interchange involution, and thus the contribution to the Grothendieck ring of varieties is
![]() $[(\mathbb {C}^*)^2/\mu _2\times S_2]$
. To determine this class, we first identify, as above,
$[(\mathbb {C}^*)^2/\mu _2\times S_2]$
. To determine this class, we first identify, as above,
![]() $(\mathbb {C}^*)^2/S_2\simeq \mathbb {C}^*\times \mathbb {C}$
by using the elementary symmetric functions. Then
$(\mathbb {C}^*)^2/S_2\simeq \mathbb {C}^*\times \mathbb {C}$
by using the elementary symmetric functions. Then
![]() $\mu _2$
action
$\mu _2$
action
![]() $(x_1,x_2)\mapsto (-x_1,-x_2)$
acts on elementary symmetric polynomials via
$(x_1,x_2)\mapsto (-x_1,-x_2)$
acts on elementary symmetric polynomials via
![]() $(x_1x_2,x_1+x_2)\mapsto (x_1x_2,-x_1-x_2)$
, and thus finally
$(x_1x_2,x_1+x_2)\mapsto (x_1x_2,-x_1-x_2)$
, and thus finally
where
![]() $\mu _2$
acts on
$\mu _2$
acts on
![]() $\mathbb {C}$
by sign, and the quotient is readily identified with
$\mathbb {C}$
by sign, and the quotient is readily identified with
![]() $\mathbb {C}$
by taking the square of the coordinate.
$\mathbb {C}$
by taking the square of the coordinate.
Altogether, we thus compute
 $$ \begin{align*}\begin{aligned} [D_{3A_2}]&=[(1)]+[(2)]+[(3)]+3[\mathbb{C}^*]+4[\mathbb{C}^0] =[\mathbb{C}^*\times\mathbb{C}^2]+2[\mathbb{C}^*\times\mathbb{C}]+3[\mathbb{C}^*]+4[\mathbb{C}^0]\\ &=[\mathbb{C}^*]\cdot \left([\mathbb{C}^*]^2+2[\mathbb{C}^*]+[\mathbb{C}^0]\right)+2[\mathbb{C}^*]\cdot\left([\mathbb{C}^*]+[\mathbb{C}^0]\right)+3[\mathbb{C}^*]+4[\mathbb{C}^0]\\ &=[\mathbb{C}^*]^3+4[\mathbb{C}^*]^2+6[\mathbb{C}^*]+4[\mathbb{C}^0]\,, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} [D_{3A_2}]&=[(1)]+[(2)]+[(3)]+3[\mathbb{C}^*]+4[\mathbb{C}^0] =[\mathbb{C}^*\times\mathbb{C}^2]+2[\mathbb{C}^*\times\mathbb{C}]+3[\mathbb{C}^*]+4[\mathbb{C}^0]\\ &=[\mathbb{C}^*]\cdot \left([\mathbb{C}^*]^2+2[\mathbb{C}^*]+[\mathbb{C}^0]\right)+2[\mathbb{C}^*]\cdot\left([\mathbb{C}^*]+[\mathbb{C}^0]\right)+3[\mathbb{C}^*]+4[\mathbb{C}^0]\\ &=[\mathbb{C}^*]^3+4[\mathbb{C}^*]^2+6[\mathbb{C}^*]+4[\mathbb{C}^0]\,, \end{aligned} \end{align*} $$
which is equal to the class
![]() $[\mathbb {P}^3]$
, as can be seen by decomposing
$[\mathbb {P}^3]$
, as can be seen by decomposing
![]() $\mathbb {P}^3$
in the usual toric way, as it is the toric variety associated with a tetrahedron, which has one highest-dimensional cell, four faces, six edges, and four vertices.
$\mathbb {P}^3$
in the usual toric way, as it is the toric variety associated with a tetrahedron, which has one highest-dimensional cell, four faces, six edges, and four vertices.
One can interpret the computations above as giving a description of the exceptional divisor
![]() $D_{3A_2}$
as the quotient of a toric threefold by the action of
$D_{3A_2}$
as the quotient of a toric threefold by the action of
![]() $S_3$
. Rather than going into the geometry of this action in detail, we sketch an alternative direct toric approach. Using this alternative approach, we can in fact identify the polytope of this toric threefold and the action of
$S_3$
. Rather than going into the geometry of this action in detail, we sketch an alternative direct toric approach. Using this alternative approach, we can in fact identify the polytope of this toric threefold and the action of
![]() $S_3$
explicitly. This gives us the added information that the toric threefold is simplicial, and provides an alternate proof of Theorem 1.3 (see Remark 8.4).
$S_3$
explicitly. This gives us the added information that the toric threefold is simplicial, and provides an alternate proof of Theorem 1.3 (see Remark 8.4).
We first note that by general theory the GIT quotient
![]() $\mathbb {P}^5/\!\!/\mathbb {T}^2$
is itself a toric variety (see [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Chap. 14]). We now describe the polytope giving us this toric variety, and the
$\mathbb {P}^5/\!\!/\mathbb {T}^2$
is itself a toric variety (see [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Chap. 14]). We now describe the polytope giving us this toric variety, and the
![]() $S_3$
action on it.
$S_3$
action on it.
Lemma 8.2 (Toric polytope).
Let
![]() $P_a$
be the polytope in
$P_a$
be the polytope in
![]() $\mathbb {Z}^3\otimes _{\mathbb {Z}}\mathbb {R}$
defined by the columns of the following matrix:
$\mathbb {Z}^3\otimes _{\mathbb {Z}}\mathbb {R}$
defined by the columns of the following matrix:
 $$ \begin{align} P_a \longleftrightarrow \left( \begin{array}{rrrrrrrr} -\frac{3}{8}&0&\frac{3}{8}&0&\frac{3}{7}&0&0&-\frac{3}{7}\\ 1&\frac{1}{7}&-\frac{7}{8}&0&-\frac{8}{7}&-\frac{1}{8}&0&1\\ 2&\frac{20}{7}&\frac{11}{4}&2&\frac{20}{7}&2&3&2\\ \end{array} \right)\ \end{align} $$
$$ \begin{align} P_a \longleftrightarrow \left( \begin{array}{rrrrrrrr} -\frac{3}{8}&0&\frac{3}{8}&0&\frac{3}{7}&0&0&-\frac{3}{7}\\ 1&\frac{1}{7}&-\frac{7}{8}&0&-\frac{8}{7}&-\frac{1}{8}&0&1\\ 2&\frac{20}{7}&\frac{11}{4}&2&\frac{20}{7}&2&3&2\\ \end{array} \right)\ \end{align} $$
and consider the action of
![]() $S_3$
on
$S_3$
on
![]() $\mathbb {Z}^3$
given by the transposition
$\mathbb {Z}^3$
given by the transposition
![]() $\tau $
and the
$\tau $
and the
![]() $3$
-cycle
$3$
-cycle
![]() $\sigma $
:
$\sigma $
:
 $$ \begin{align} \tau=\left(\begin{array}{rrr} -1&0&0\\ 5&1&0\\ -2&0&1\\ \end{array} \right), \ \ \sigma = \left( \begin{array}{rrr} -8&-3&0\\ 19&7&0\\ -16&-6&1\\ \end{array} \right). \end{align} $$
$$ \begin{align} \tau=\left(\begin{array}{rrr} -1&0&0\\ 5&1&0\\ -2&0&1\\ \end{array} \right), \ \ \sigma = \left( \begin{array}{rrr} -8&-3&0\\ 19&7&0\\ -16&-6&1\\ \end{array} \right). \end{align} $$
The polytope
![]() $P_a$
is a combinatorial cube, the associated toric variety
$P_a$
is a combinatorial cube, the associated toric variety
![]() $X_{P_a}$
is simplicial, and the quotient of
$X_{P_a}$
is simplicial, and the quotient of
![]() $X_{P_a}$
by the induced action of
$X_{P_a}$
by the induced action of
![]() $S_3$
is isomorphic to
$S_3$
is isomorphic to
![]() $D_{3A_2}$
; that is,
$D_{3A_2}$
; that is,
Remark 8.3. Strictly speaking, to define
![]() $X_{P_a}$
, we must first clear denominators to obtain a convex lattice polytope, but scaling the polytope does not affect the abstract variety, it only affects the polarization.
$X_{P_a}$
, we must first clear denominators to obtain a convex lattice polytope, but scaling the polytope does not affect the abstract variety, it only affects the polarization.
Proof. From the Kirwan construction, and the Luna Slice Theorem, identifying the exceptional divisor in the blowup of the Luna slice at the origin with
![]() $\mathbb {P}^5$
gives
$\mathbb {P}^5$
gives
![]() $D_{3A_2}\cong \mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(1)}\operatorname {Stab}(S_{3A_2})$
(see Lemmas 3.4 and 3.3). Note that in principle, from the Kirwan construction, one only has that the action of the stabilizer lifts to give a linearization on some positive tensor power of
$D_{3A_2}\cong \mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(1)}\operatorname {Stab}(S_{3A_2})$
(see Lemmas 3.4 and 3.3). Note that in principle, from the Kirwan construction, one only has that the action of the stabilizer lifts to give a linearization on some positive tensor power of
![]() $\mathcal {O}_{\mathbb {P}^5}(1)$
, but the lift of the action to
$\mathcal {O}_{\mathbb {P}^5}(1)$
, but the lift of the action to
![]() $\mathcal {O}_{\mathbb {P}^5}(1)$
is evident from the given explicit formula for the action, and of course which positive tensor power one uses will not change the GIT quotient. From the description of the stabilizer in Lemma 3.3, we can conclude that
$\mathcal {O}_{\mathbb {P}^5}(1)$
is evident from the given explicit formula for the action, and of course which positive tensor power one uses will not change the GIT quotient. From the description of the stabilizer in Lemma 3.3, we can conclude that
![]() $D_{3A_2}\cong (\mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(1)} (\mathbb {C}^*)^2)/S_3$
. In order to keep track of the
$D_{3A_2}\cong (\mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(1)} (\mathbb {C}^*)^2)/S_3$
. In order to keep track of the
![]() $S_3$
action, we prefer to use the linearization on
$S_3$
action, we prefer to use the linearization on
![]() $\mathcal {O}_{\mathbb {P}^5}(3)$
.
$\mathcal {O}_{\mathbb {P}^5}(3)$
.
Our first goal therefore is to describe the toric variety
![]() $\mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(3)} (\mathbb {C}^*)^2$
. To start, we claim that the action of
$\mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(3)} (\mathbb {C}^*)^2$
. To start, we claim that the action of
![]() $(\mathbb {C}^*)^2$
on
$(\mathbb {C}^*)^2$
on
![]() $\mathbb {P}^5$
is induced by the natural action on the Luna slice
$\mathbb {P}^5$
is induced by the natural action on the Luna slice
![]() $\mathbb {C}^6$
, so that fixing the inclusion of tori
$\mathbb {C}^6$
, so that fixing the inclusion of tori
![]() $\mathbb {C}^*\times (\mathbb {C}^*)^2\to (\mathbb {C}^*)^6$
given by the matrix
$\mathbb {C}^*\times (\mathbb {C}^*)^2\to (\mathbb {C}^*)^6$
given by the matrix
 $$ \begin{align*}\gamma= \left( \begin{array}{rrrrrr} 1&1&1&1&1&1\\ -3&3&0&-2&2&0\\ -3&0&3&-2&0&2\\ \end{array} \right)\,, \end{align*} $$
$$ \begin{align*}\gamma= \left( \begin{array}{rrrrrr} 1&1&1&1&1&1\\ -3&3&0&-2&2&0\\ -3&0&3&-2&0&2\\ \end{array} \right)\,, \end{align*} $$
and the character
![]() $\chi :\mathbb {C}^*\times (\mathbb {C}^*)^2\to \mathbb {C}^*$
defined by
$\chi :\mathbb {C}^*\times (\mathbb {C}^*)^2\to \mathbb {C}^*$
defined by
![]() $\chi (t,\lambda _1,\lambda _2)=t^3$
, one has an identification of GIT quotients
$\chi (t,\lambda _1,\lambda _2)=t^3$
, one has an identification of GIT quotients
![]() $\mathbb {C}^6/\!\!/_\chi (\mathbb {C}^*\times (\mathbb {C}^*)^2) = \mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(3)} (\mathbb {C}^*)^2$
(invariant sections of tensor powers of the trivial line bundle
$\mathbb {C}^6/\!\!/_\chi (\mathbb {C}^*\times (\mathbb {C}^*)^2) = \mathbb {P}^5/\!\!/_{\mathcal {O}_{\mathbb {P}^5}(3)} (\mathbb {C}^*)^2$
(invariant sections of tensor powers of the trivial line bundle
![]() $\mathbb {C}^6\times \mathbb {C}$
over
$\mathbb {C}^6\times \mathbb {C}$
over
![]() $\mathbb {C}^6$
with respect to the character
$\mathbb {C}^6$
with respect to the character
![]() $\chi $
are canonically identified with the invariant sections of tensor powers of
$\chi $
are canonically identified with the invariant sections of tensor powers of
![]() $\mathcal {O}_{\mathbb {P}^5}(3)$
; see, e.g., [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Lem. 14.1.1(b)]). Using the technique in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Chap. 14], one sees that
$\mathcal {O}_{\mathbb {P}^5}(3)$
; see, e.g., [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Lem. 14.1.1(b)]). Using the technique in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Chap. 14], one sees that
![]() $\mathbb {C}^6/\!\!/_\chi (\mathbb {C}^*\times (\mathbb {C}^*)^2)$
is the toric variety associated to a three-dimensional polytope obtained in the following way.
$\mathbb {C}^6/\!\!/_\chi (\mathbb {C}^*\times (\mathbb {C}^*)^2)$
is the toric variety associated to a three-dimensional polytope obtained in the following way.
One defines a lattice M by the exact sequence
Then, considering the composition
![]() $\mathbb {C}^*\times (\mathbb {C}^*)^2\to (\mathbb {C}^*)^6 \to \mathbb {C}^*$
, where the first map is the inclusion of tori determined by
$\mathbb {C}^*\times (\mathbb {C}^*)^2\to (\mathbb {C}^*)^6 \to \mathbb {C}^*$
, where the first map is the inclusion of tori determined by
![]() $\gamma $
, and the second map of tori is determined by the matrix
$\gamma $
, and the second map of tori is determined by the matrix
one sees that the composition is the character
![]() $\chi $
given above. From [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Chap. 14], one sees that the quotient
$\chi $
given above. From [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Chap. 14], one sees that the quotient
![]() $\mathbb {C}^6/\!\!/_\chi (\mathbb {C}^*\times (\mathbb {C}^*)^2)$
is the toric variety associated with the lattice M and the polytope
$\mathbb {C}^6/\!\!/_\chi (\mathbb {C}^*\times (\mathbb {C}^*)^2)$
is the toric variety associated with the lattice M and the polytope
where
![]() $e_i$
is the standard dual coordinate and the
$e_i$
is the standard dual coordinate and the
![]() $a_i$
are the entries of the vector a. The
$a_i$
are the entries of the vector a. The
![]() $S_3$
action on
$S_3$
action on
![]() $\mathbb {C}^6$
(see Lemma 3.4) induces the
$\mathbb {C}^6$
(see Lemma 3.4) induces the
![]() $S_3$
action on
$S_3$
action on
![]() $(\mathbb {C}^*)^6$
, and therefore on
$(\mathbb {C}^*)^6$
, and therefore on
![]() $\mathbb {Z}^6$
, and in turn determines an
$\mathbb {Z}^6$
, and in turn determines an
![]() $S_3$
action on M.
$S_3$
action on M.
The columns of the following matrix give an integral basis of M:
 $$ \begin{align*}\left(\!\!\!\!\!\!\begin{array}{rrr} 0&0&1\\ -2&0&1\\ -16& -6&1\\ -3&-1&-1\\ 0&-1&-1\\ 21&8&-1 \end{array} \right) \end{align*} $$
$$ \begin{align*}\left(\!\!\!\!\!\!\begin{array}{rrr} 0&0&1\\ -2&0&1\\ -16& -6&1\\ -3&-1&-1\\ 0&-1&-1\\ 21&8&-1 \end{array} \right) \end{align*} $$
and therefore, identifying M with
![]() $\mathbb {Z}^3$
using this basis, we may identify
$\mathbb {Z}^3$
using this basis, we may identify
![]() $P_a$
as the set of
$P_a$
as the set of
![]() $(a,b,c)\in \mathbb {R}^3$
such that
$(a,b,c)\in \mathbb {R}^3$
such that
 $$ \begin{align*}\begin{array}{rcrcrcr} &&&&c&\ge&2,\\ -2a&&&+&c&\ge&2,\\ -16a&-&6b&+&c&\ge&2,\\ -3a&-&b&-&c&\ge&-3,\\ &&-b&-&c&\ge&-3,\\ 21a&+&8b&-&c&\ge&-3.\\ \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{rcrcrcr} &&&&c&\ge&2,\\ -2a&&&+&c&\ge&2,\\ -16a&-&6b&+&c&\ge&2,\\ -3a&-&b&-&c&\ge&-3,\\ &&-b&-&c&\ge&-3,\\ 21a&+&8b&-&c&\ge&-3.\\ \end{array} \end{align*} $$
From this, one can identify
![]() $P_a$
with the convex hull of eight vertices, given by the columns of the matrix given in (8.1).Footnote
1
$P_a$
with the convex hull of eight vertices, given by the columns of the matrix given in (8.1).Footnote
1
The polytope
![]() $P_a$
is combinatorially a cube; for instance, the first four columns and last four columns give top and bottom faces of the combinatorial cube, respectively, and the vectors with last coordinate equal to
$P_a$
is combinatorially a cube; for instance, the first four columns and last four columns give top and bottom faces of the combinatorial cube, respectively, and the vectors with last coordinate equal to
![]() $2$
give a side face of the cube. Considering the dictionary between polytopes and fans (e.g., [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, p. 75]), it is elementary to check that the toric variety associated with
$2$
give a side face of the cube. Considering the dictionary between polytopes and fans (e.g., [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, p. 75]), it is elementary to check that the toric variety associated with
![]() $P_a$
, being a combinatorial cube, is simplicial.
$P_a$
, being a combinatorial cube, is simplicial.
Finally, in these coordinates, the
![]() $S_3$
action on M, identified with
$S_3$
action on M, identified with
![]() $\mathbb {Z}^3$
, is given by the transposition
$\mathbb {Z}^3$
, is given by the transposition
![]() $\tau $
and
$\tau $
and
![]() $3$
-cycle
$3$
-cycle
![]() $\sigma $
given in (8.2).
$\sigma $
given in (8.2).
Remark 8.4 (Class in the Grothendieck ring).
In the terminology of Lemma 8.2, we note that the vectors
![]() $(0,1,-1)$
,
$(0,1,-1)$
,
![]() $(3,-8,-1)$
, and
$(3,-8,-1)$
, and
![]() $(-3,7,-7)$
define a rank
$(-3,7,-7)$
define a rank
![]() $3$
, index
$3$
, index
![]() $27$
sublattice of
$27$
sublattice of
![]() $\mathbb {Z}^3$
on which
$\mathbb {Z}^3$
on which
![]() $S_3$
acts via
$S_3$
acts via
![]() $\tau $
and
$\tau $
and
![]() $\sigma $
by the standard permutation of vectors. Moreover, one can check directly that the action of
$\sigma $
by the standard permutation of vectors. Moreover, one can check directly that the action of
![]() $S_3$
on the vertices of the combinatorial cube defining
$S_3$
on the vertices of the combinatorial cube defining
![]() $P_a$
corresponds to the standard action of
$P_a$
corresponds to the standard action of
![]() $S_3$
on a cube, fixing two antipodal vertices, and in particular acts by toric automorphisms. In this situation, it is the antipodal vertices
$S_3$
on a cube, fixing two antipodal vertices, and in particular acts by toric automorphisms. In this situation, it is the antipodal vertices
![]() $(0,0,3)$
and
$(0,0,3)$
and
![]() $(0,0,2)$
of
$(0,0,2)$
of
![]() $P_a$
that are fixed. At the same time, taking the basis
$P_a$
that are fixed. At the same time, taking the basis
![]() $(0,0,1)$
,
$(0,0,1)$
,
![]() $(-1,3,0)$
,
$(-1,3,0)$
,
![]() $(1,-2,2)$
for
$(1,-2,2)$
for
![]() $\mathbb {Z}^3$
, we have that the action of
$\mathbb {Z}^3$
, we have that the action of
![]() $S_3$
in these coordinates is given by the matrices
$S_3$
in these coordinates is given by the matrices
 $$ \begin{align*}\tau=\left(\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1\\ \end{array} \right), \ \ \sigma = \left( \begin{array}{rrr} 0&1&0\\ -1&-1&0\\ 0&0&1\\ \end{array} \right). \end{align*} $$
$$ \begin{align*}\tau=\left(\begin{array}{ccc} 0&1&0\\ 1&0&0\\ 0&0&1\\ \end{array} \right), \ \ \sigma = \left( \begin{array}{rrr} 0&1&0\\ -1&-1&0\\ 0&0&1\\ \end{array} \right). \end{align*} $$
From this, using the dictionary between faces of polytopes and torus orbits, one can easily work out the action of
![]() $S_3$
on all the torus orbits of
$S_3$
on all the torus orbits of
![]() $X_{P_a}$
, as well as their quotients, and consequently, re-derive the class of
$X_{P_a}$
, as well as their quotients, and consequently, re-derive the class of
![]() $X_{P_a}/S_3\cong D_{3A_2}$
in the Grothendieck ring. For instance, it is immediate from the action of the matrices above that the quotient of the maximal torus
$X_{P_a}/S_3\cong D_{3A_2}$
in the Grothendieck ring. For instance, it is immediate from the action of the matrices above that the quotient of the maximal torus
![]() $(\mathbb {C}^*)^3/S_3$
is
$(\mathbb {C}^*)^3/S_3$
is
![]() $\mathbb {C}^2\times \mathbb {C}^*$
, and similarly, that the two-dimensional tori contribute
$\mathbb {C}^2\times \mathbb {C}^*$
, and similarly, that the two-dimensional tori contribute
![]() $(\mathbb {C}^*)^2/S_2$
with quotient
$(\mathbb {C}^*)^2/S_2$
with quotient
![]() $\mathbb {C}\times \mathbb {C}^*$
, and that the one-dimensional tori contribute quotients of
$\mathbb {C}\times \mathbb {C}^*$
, and that the one-dimensional tori contribute quotients of
![]() $\mathbb {C}^*$
by subgroups, each giving
$\mathbb {C}^*$
by subgroups, each giving
![]() $\mathbb {C}^*$
. Adding up all of the contributions in the Grothendieck ring gives the same class as
$\mathbb {C}^*$
. Adding up all of the contributions in the Grothendieck ring gives the same class as
![]() $\mathbb {P}^3$
. This gives an alternate proof of Lemma 8.1, and therefore of Theorem 1.3.
$\mathbb {P}^3$
. This gives an alternate proof of Lemma 8.1, and therefore of Theorem 1.3.
It turns out that one can use Theorem 1.3 and Lemma 8.2 to recover the fact that the Betti numbers of
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
are equal. Of course, the Betti numbers of
${\overline {\mathcal {B}_4/\Gamma }}$
are equal. Of course, the Betti numbers of
![]() ${\mathcal {M}}^{\operatorname {K}}$
were already computed in [Reference KirwanKi2] and [Reference ZhangZha] (see also [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, (C.2)] to reconcile the numbers in those two papers), and the Betti numbers of
${\mathcal {M}}^{\operatorname {K}}$
were already computed in [Reference KirwanKi2] and [Reference ZhangZha] (see also [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, (C.2)] to reconcile the numbers in those two papers), and the Betti numbers of
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
were computed in our paper [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, Th. C.1], but the proof of the following corollary helps to give a more intuitive reason for the agreement of the Betti numbers.
${\overline {\mathcal {B}_4/\Gamma }}$
were computed in our paper [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, Th. C.1], but the proof of the following corollary helps to give a more intuitive reason for the agreement of the Betti numbers.
Corollary 8.5. The Kirwan compactification
![]() ${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
${\mathcal {M}}^{\operatorname {K}}$
and the toroidal compactification
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
of the moduli space of smooth cubic surfaces
${\overline {\mathcal {B}_4/\Gamma }}$
of the moduli space of smooth cubic surfaces
![]() $\mathcal {M}$
have the same Betti numbers.
$\mathcal {M}$
have the same Betti numbers.
Proof. First, we claim that
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
have no odd cohomology. This follows from the fact that
${\overline {\mathcal {B}_4/\Gamma }}$
have no odd cohomology. This follows from the fact that
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
has no odd cohomology, together with the decomposition theorem and the fact that the exceptional divisors for
${\mathcal {M}}^{\operatorname {GIT}}$
has no odd cohomology, together with the decomposition theorem and the fact that the exceptional divisors for
![]() $\pi :{\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
and
$\pi :{\mathcal {M}}^{\operatorname {K}}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
and
![]() $p:{\overline {\mathcal {B}_4/\Gamma }}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
are quotients of simplicial toric varieties by finite groups [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Th. 12.3.11] (for
$p:{\overline {\mathcal {B}_4/\Gamma }}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
are quotients of simplicial toric varieties by finite groups [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCLS, Th. 12.3.11] (for
![]() ${\mathcal {M}}^{\operatorname {K}}$
, Lemma 8.2 shows that the exceptional divisor
${\mathcal {M}}^{\operatorname {K}}$
, Lemma 8.2 shows that the exceptional divisor
![]() $D_{3A_2}$
is a finite quotient of a simplicial toric variety, whereas for
$D_{3A_2}$
is a finite quotient of a simplicial toric variety, whereas for
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
, the exceptional divisor
${\overline {\mathcal {B}_4/\Gamma }}$
, the exceptional divisor
![]() $T_{3A_2}$
is simply equal to
$T_{3A_2}$
is simply equal to
![]() $\mathbb {P}^3$
, by Corollary 4.9). The decomposition theorem also gives
$\mathbb {P}^3$
, by Corollary 4.9). The decomposition theorem also gives
![]() $\dim H^2({\mathcal {M}}^{\operatorname {K}})=\dim H^2({\mathcal {M}}^{\operatorname {GIT}})+1= \dim H^2({\overline {\mathcal {B}_4/\Gamma }})$
. Finally, it remains to determine the cohomology in the middle degree 4, and the agreement
$\dim H^2({\mathcal {M}}^{\operatorname {K}})=\dim H^2({\mathcal {M}}^{\operatorname {GIT}})+1= \dim H^2({\overline {\mathcal {B}_4/\Gamma }})$
. Finally, it remains to determine the cohomology in the middle degree 4, and the agreement
![]() $\dim H^4({\mathcal {M}}^{\operatorname {K}})=\dim H^4({\overline {\mathcal {B}_4/\Gamma }})$
then follows from the fact that the topological Euler characteristic for cohomology with compact supports is well-defined on the Grothendieck ring.
$\dim H^4({\mathcal {M}}^{\operatorname {K}})=\dim H^4({\overline {\mathcal {B}_4/\Gamma }})$
then follows from the fact that the topological Euler characteristic for cohomology with compact supports is well-defined on the Grothendieck ring.
Remark 8.6. Note that this also gives a short method of computing the rational cohomology of
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
and
${\overline {\mathcal {B}_4/\Gamma }}$
and
![]() ${\mathcal {M}}^{\operatorname {K}}$
. Indeed,
${\mathcal {M}}^{\operatorname {K}}$
. Indeed,
![]() ${\mathcal {M}}^{\operatorname {GIT}}$
is a weighted projective space, and so has the rational cohomology of
${\mathcal {M}}^{\operatorname {GIT}}$
is a weighted projective space, and so has the rational cohomology of
![]() $\mathbb {P}^4$
. From the decomposition theorem, and the fact that
$\mathbb {P}^4$
. From the decomposition theorem, and the fact that
![]() ${\overline {\mathcal {B}_4/\Gamma }}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
has exceptional divisor equal to
${\overline {\mathcal {B}_4/\Gamma }}\rightarrow {\mathcal {M}}^{\operatorname {GIT}}$
has exceptional divisor equal to
![]() $\mathbb {P}^3$
, it follows that
$\mathbb {P}^3$
, it follows that
![]() $\dim H^0({\overline {\mathcal {B}_4/\Gamma }})=\dim H^8({\overline {\mathcal {B}_4/\Gamma }})= 1$
,
$\dim H^0({\overline {\mathcal {B}_4/\Gamma }})=\dim H^8({\overline {\mathcal {B}_4/\Gamma }})= 1$
,
![]() $\dim H^2({\overline {\mathcal {B}_4/\Gamma }})=\dim H^6({\overline {\mathcal {B}_4/\Gamma }}) = 2$
, and
$\dim H^2({\overline {\mathcal {B}_4/\Gamma }})=\dim H^6({\overline {\mathcal {B}_4/\Gamma }}) = 2$
, and
![]() $\dim H^4({\overline {\mathcal {B}_4/\Gamma }})=2$
. This determines the cohomology of
$\dim H^4({\overline {\mathcal {B}_4/\Gamma }})=2$
. This determines the cohomology of
![]() ${\mathcal {M}}^{\operatorname {K}}$
via Corollary 8.5.
${\mathcal {M}}^{\operatorname {K}}$
via Corollary 8.5.
Appendix A. Luna slice computations for the GIT model for cubic surfaces
In this appendix, we give the detailed proofs of some of the statements from §3. While the results of these computations are crucial for our argument, the method is by explicit computations in local charts on the exceptional divisors, and we have put the calculations here in order not to interrupt the line of thought of our arguments in §3.
A.1 Proof of Lemma 3.3
While this proof is parallel to the case of the
![]() $3D_4$
cubic threefold, which was treated in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, Prop. B.6], we still give the complete details, as the careful identification of the finite groups involved is essential in our argument.
$3D_4$
cubic threefold, which was treated in [Reference Casalaina-Martin, Grushevsky, Hulek and LazaCMG+1, Prop. B.6], we still give the complete details, as the careful identification of the finite groups involved is essential in our argument.
We first determine the stabilizer group
![]() $\operatorname {GL}(S_{3A_2})\subseteq \operatorname {GL}(4,\mathbb {C})$
. To begin, it is clear that the group
$\operatorname {GL}(S_{3A_2})\subseteq \operatorname {GL}(4,\mathbb {C})$
. To begin, it is clear that the group
 $$ \begin{align} \left\{\left( \begin{array}{c|c} \mathbb{S}_3&\\ \hline &\mathbb{C}^*\\ \end{array} \right): \lambda_0\lambda_1\lambda_2=\lambda_3^3\right\}\subseteq \operatorname{GL}(4,\mathbb{C}) \end{align} $$
$$ \begin{align} \left\{\left( \begin{array}{c|c} \mathbb{S}_3&\\ \hline &\mathbb{C}^*\\ \end{array} \right): \lambda_0\lambda_1\lambda_2=\lambda_3^3\right\}\subseteq \operatorname{GL}(4,\mathbb{C}) \end{align} $$
stabilizes
![]() $S_{3A_2}$
. We wish to show that the stabilizer is equal to this group. For this, we observe that any symmetry must permute the three singularities of the cubic
$S_{3A_2}$
. We wish to show that the stabilizer is equal to this group. For this, we observe that any symmetry must permute the three singularities of the cubic
![]() $S_{3A_2}$
, that is, the points
$S_{3A_2}$
, that is, the points
![]() $(1:0:0:0)$
,
$(1:0:0:0)$
,
![]() $(0:1:0:0)$
, and
$(0:1:0:0)$
, and
![]() $(0:0:1:0)$
. This forces a matrix stabilizing
$(0:0:1:0)$
. This forces a matrix stabilizing
![]() $S_{3A_2}$
to be of the form
$S_{3A_2}$
to be of the form
 $$ \begin{align*}\left( \begin{array}{c|c} \mathbb{S}_3&*\\ \hline 0&\lambda_3\\ \end{array} \right)\,. \end{align*} $$
$$ \begin{align*}\left( \begin{array}{c|c} \mathbb{S}_3&*\\ \hline 0&\lambda_3\\ \end{array} \right)\,. \end{align*} $$
Such a transformation sends the monomial
![]() $x_0x_1x_2$
to
$x_0x_1x_2$
to
![]() $(\lambda _0 x_0+*x_3)\cdot (\lambda _1 x_1+*x_3)\cdot (\lambda _2 x_2+*x_3)$
, where all the
$(\lambda _0 x_0+*x_3)\cdot (\lambda _1 x_1+*x_3)\cdot (\lambda _2 x_2+*x_3)$
, where all the
![]() $\lambda $
’s are nonzero, and
$\lambda $
’s are nonzero, and
![]() $*$
are the entries of the unknown
$*$
are the entries of the unknown
![]() $1\times 3$
block of the matrix. Furthermore,
$1\times 3$
block of the matrix. Furthermore,
![]() $x_3$
is sent to
$x_3$
is sent to
![]() $\lambda _3 x_3$
. Thus, all entries
$\lambda _3 x_3$
. Thus, all entries
![]() $*$
must be equal to zero; otherwise applying this transformation to
$*$
must be equal to zero; otherwise applying this transformation to
![]() $S_{3A_2}$
would give a cubic with nonzero coefficient of some monomial
$S_{3A_2}$
would give a cubic with nonzero coefficient of some monomial
![]() $x_ax_b x_3$
with
$x_ax_b x_3$
with
![]() $0\le a<b\le 2$
. Thus, we have deduced that the matrix stabilizing
$0\le a<b\le 2$
. Thus, we have deduced that the matrix stabilizing
![]() $S_{3A_2}$
must actually be of the form
$S_{3A_2}$
must actually be of the form
 $$ \begin{align*}\left( \begin{array}{c|c} \mathbb{S}_3&0\\ \hline 0&\lambda_3\\ \end{array} \right)\,. \end{align*} $$
$$ \begin{align*}\left( \begin{array}{c|c} \mathbb{S}_3&0\\ \hline 0&\lambda_3\\ \end{array} \right)\,. \end{align*} $$
Finally, it is obvious that any element of the stabilizer satisfies the condition
![]() $\lambda _0\lambda _1\lambda _2=\lambda _3^3$
. This completes the proof that the stabilizer group
$\lambda _0\lambda _1\lambda _2=\lambda _3^3$
. This completes the proof that the stabilizer group
![]() $\operatorname {GL}(S_{3A_2}) \subseteq \operatorname {GL}(4,\mathbb {C})$
is as claimed. The description of
$\operatorname {GL}(S_{3A_2}) \subseteq \operatorname {GL}(4,\mathbb {C})$
is as claimed. The description of
![]() $\operatorname {Stab}(S_{3A_2}) \subseteq \operatorname {SL}(4,\mathbb {C})$
follows immediately.
$\operatorname {Stab}(S_{3A_2}) \subseteq \operatorname {SL}(4,\mathbb {C})$
follows immediately.
(2) This is immediate since
![]() $\operatorname {Aut}(S_{3A_2})$
is naturally a subgroup of
$\operatorname {Aut}(S_{3A_2})$
is naturally a subgroup of
![]() $\operatorname {PGL}(4,\mathbb {C})$
.
$\operatorname {PGL}(4,\mathbb {C})$
.
(3) We now want to describe the structure of the stabilizer group
![]() $\operatorname {GL}(S_{3A_2})\subseteq \operatorname {GL}(4,\mathbb {C})$
more precisely. There is clearly a short exact sequence
$\operatorname {GL}(S_{3A_2})\subseteq \operatorname {GL}(4,\mathbb {C})$
more precisely. There is clearly a short exact sequence
where D is the subgroup of diagonal matrices in
![]() $\operatorname {GL}(S_{3A_2})$
, and the map to
$\operatorname {GL}(S_{3A_2})$
, and the map to
![]() $S_3$
is the one taking a generalized permutation matrix to the associated permutation. There is an obvious section
$S_3$
is the one taking a generalized permutation matrix to the associated permutation. There is an obvious section
![]() $S_3\to \operatorname {GL}(S_{3A_2})$
, viewing
$S_3\to \operatorname {GL}(S_{3A_2})$
, viewing
![]() $S_3$
as block diagonal permutation matrices. This gives the identification
$S_3$
as block diagonal permutation matrices. This gives the identification
where the action of
![]() $S_3$
on D is to permute the first three entries. The surjection of
$S_3$
on D is to permute the first three entries. The surjection of
![]() $\operatorname {Stab}(S_{3A_2})$
onto
$\operatorname {Stab}(S_{3A_2})$
onto
![]() $S_3$
can be seen by the matrices
$S_3$
can be seen by the matrices
 $$ \begin{align*}\left( \begin{array}{cccc} 0&1&0&0\\ 1& 0&0&0\\ 0&0&\zeta_8^{3}&0\\ 0&0&0&\zeta_8 \end{array} \right) \qquad \left( \begin{array}{cccc} 0& 0&1&0\\ 1& 0&0&0\\ 0&1&0&0\\ 0&0&0&1 \end{array} \right)\,, \end{align*} $$
$$ \begin{align*}\left( \begin{array}{cccc} 0&1&0&0\\ 1& 0&0&0\\ 0&0&\zeta_8^{3}&0\\ 0&0&0&\zeta_8 \end{array} \right) \qquad \left( \begin{array}{cccc} 0& 0&1&0\\ 1& 0&0&0\\ 0&1&0&0\\ 0&0&0&1 \end{array} \right)\,, \end{align*} $$
where
![]() $\zeta _8$
is a primitive
$\zeta _8$
is a primitive
![]() $8$
th root of unity.
$8$
th root of unity.
(4) The identification
![]() $\operatorname {GL}(S_{3A_2})^\circ = D$
comes from (3.15) and the identification
$\operatorname {GL}(S_{3A_2})^\circ = D$
comes from (3.15) and the identification
![]() $D\cong \mathbb {T}^3$
. We then obtain the isomorphism
$D\cong \mathbb {T}^3$
. We then obtain the isomorphism
![]() $\operatorname {GL}(S_{3A_2})/\operatorname {GL}(S_{3A_2})^\circ \cong S_3$
from (3.15), as well.
$\operatorname {GL}(S_{3A_2})/\operatorname {GL}(S_{3A_2})^\circ \cong S_3$
from (3.15), as well.
The isomorphism
![]() $\operatorname {Aut}(S_{3A_2})/\operatorname {Aut}(S_{3A_2})^\circ \cong S_3$
then comes from (3.14). Indeed, taking connected components of the identity, we have
$\operatorname {Aut}(S_{3A_2})/\operatorname {Aut}(S_{3A_2})^\circ \cong S_3$
then comes from (3.14). Indeed, taking connected components of the identity, we have

The surjection on the right in the top row is standard (say coming from looking at the dimensions of the connected components), and the identification of the kernels of the two rows is elementary in this case since
![]() $\mathbb {C}^*$
is connected. Then one applies the Snake Lemma.
$\mathbb {C}^*$
is connected. Then one applies the Snake Lemma.
The short exact sequence (3.17) follows from (3.15) and the description
![]() $D'\cong \mathbb {T}^2\times \mu _4$
.
$D'\cong \mathbb {T}^2\times \mu _4$
.
A.2 Proof of Lemma 3.5
The Luna Slice Theorem implies that we can compute in the Luna slice. More precisely, we mean the following. First, in order to have shorter, more standard notation (e.g., to match the discussion of the Luna Slice Theorem in [Reference MukaiMFK, p. 198]), let us set
,
,
![]() $x\in X$
the point corresponding to the
$x\in X$
the point corresponding to the
![]() $3A_2$
cubic
$3A_2$
cubic
![]() $S_{3A_2}$
,
$S_{3A_2}$
,
, and
![]() $W\subseteq X$
the Luna slice. Then there is an open affine neighborhood
$W\subseteq X$
the Luna slice. Then there is an open affine neighborhood
![]() $U\subseteq X$
of x such that U is étale equivalent to
$U\subseteq X$
of x such that U is étale equivalent to
![]() $(G\times W)/G_x$
, and since
$(G\times W)/G_x$
, and since
![]() $G\times W\to (G\times W)/G_x$
is a principal
$G\times W\to (G\times W)/G_x$
is a principal
![]() $G_x$
-bundle (e.g., [Reference MukaiMFK, Cor. p. 199]), it follows that, up to a smooth factor, U is étale equivalent to
$G_x$
-bundle (e.g., [Reference MukaiMFK, Cor. p. 199]), it follows that, up to a smooth factor, U is étale equivalent to
![]() $G\times W$
. In other words, we have a diagram
$G\times W$
. In other words, we have a diagram

Since the Eckardt divisor
![]() $R\subseteq X$
is an irreducible effective divisor, preserved by the action of G, it is elementary to check that
$R\subseteq X$
is an irreducible effective divisor, preserved by the action of G, it is elementary to check that
![]() $R|_U$
is the image of
$R|_U$
is the image of
![]() $G\times (R\cap W)$
under the map
$G\times (R\cap W)$
under the map
![]() $G\times W\to U$
, where we take the reduced induced scheme structure on
$G\times W\to U$
, where we take the reduced induced scheme structure on
![]() $R\cap W$
. In other words, up to a smooth factor,
$R\cap W$
. In other words, up to a smooth factor,
![]() $R|_U$
is étale equivalent to
$R|_U$
is étale equivalent to
![]() $G\times (R\cap W)$
. Then, since
$G\times (R\cap W)$
. Then, since
![]() $G\times (R\cap W)$
is, up to a smooth factor, étale equivalent to
$G\times (R\cap W)$
is, up to a smooth factor, étale equivalent to
![]() $R\cap W$
, we conclude that
$R\cap W$
, we conclude that
![]() $\mu $
is the multiplicity of
$\mu $
is the multiplicity of
![]() $R\cap W$
at the origin.
$R\cap W$
at the origin.
We shall now apply this to the Luna slice in our case. We recall from our discussion in §3.1 that the Eckardt divisor is the divisorial locus containing all smooth cubics with an extra automorphism, smooth cubic surfaces with extra automorphisms, so it suffices to describe the locus of cubic surfaces in the Luna slice that have extra automorphisms.
Translating into the action of
![]() $\operatorname {SL}(4,\mathbb {C})$
, it suffices to describe the locus of cubic surfaces in the Luna slice with stabilizer group strictly containing the diagonal
$\operatorname {SL}(4,\mathbb {C})$
, it suffices to describe the locus of cubic surfaces in the Luna slice with stabilizer group strictly containing the diagonal
![]() $\mu _4$
. Since we are only interested in this locus in a neighborhood of the
$\mu _4$
. Since we are only interested in this locus in a neighborhood of the
![]() $3A_2$
cubic surface, we can use the fact from the Luna Slice Theorem that in a neighborhood of the origin in the Luna slice, the stabilizer groups must be subgroups of
$3A_2$
cubic surface, we can use the fact from the Luna Slice Theorem that in a neighborhood of the origin in the Luna slice, the stabilizer groups must be subgroups of
![]() $\operatorname {Stab}(S_{3A_2})$
.
$\operatorname {Stab}(S_{3A_2})$
.
Since the general point of the Eckardt divisor parameterizes cubic surfaces with a
![]() $\mathbb {Z}_2$
automorphism group, we will first describe all subgroups of
$\mathbb {Z}_2$
automorphism group, we will first describe all subgroups of
![]() $\operatorname {Stab}(S_{3A_2})$
whose image in
$\operatorname {Stab}(S_{3A_2})$
whose image in
![]() $\operatorname {PGL}(4,\mathbb {C})$
is of order
$\operatorname {PGL}(4,\mathbb {C})$
is of order
![]() $2$
. Given such a subgroup, there is a matrix A in the group such that the image of A in
$2$
. Given such a subgroup, there is a matrix A in the group such that the image of A in
![]() $\operatorname {PGL}(4,\mathbb {C})$
has order
$\operatorname {PGL}(4,\mathbb {C})$
has order
![]() $2$
. Let us classify these matrices. First, considering the sequence
$2$
. Let us classify these matrices. First, considering the sequence
we have
![]() $\langle A\rangle \cap \mu _4$
is one of
$\langle A\rangle \cap \mu _4$
is one of
![]() $\{Id\}$
,
$\{Id\}$
,
![]() $\{Id,-Id\}$
, or
$\{Id,-Id\}$
, or
![]() $\mu _4$
, so that
$\mu _4$
, so that
Then, considering the diagram

we see that A must map to an element of
![]() $S_3$
of order a power of
$S_3$
of order a power of
![]() $2$
, that is, either the identity or a transposition.
$2$
, that is, either the identity or a transposition.
Thus, there are two cases. We have
 $$ \begin{align*}\text{Case I: }\ \ \ \ A=\left( \begin{array}{cccc} \lambda_0& 0&0&0\\ 0&\lambda_1&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)\ \ \ \ \lambda_0\lambda_1\lambda_2=\lambda_3^3, \ \ \lambda_0\lambda_1\lambda_2\lambda_3=1 \end{align*} $$
$$ \begin{align*}\text{Case I: }\ \ \ \ A=\left( \begin{array}{cccc} \lambda_0& 0&0&0\\ 0&\lambda_1&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)\ \ \ \ \lambda_0\lambda_1\lambda_2=\lambda_3^3, \ \ \lambda_0\lambda_1\lambda_2\lambda_3=1 \end{align*} $$
and, up to changing indices for the transposition,
 $$ \begin{align*}\text{Case II: }\ \ \ \ A=\left( \begin{array}{cccc} 0&\lambda_1&0&0\\ \lambda_0& 0&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)\ \ \ \ \lambda_0\lambda_1\lambda_2=\lambda_3^3, \ \ \lambda_0\lambda_1\lambda_2\lambda_3=-1\,. \end{align*} $$
$$ \begin{align*}\text{Case II: }\ \ \ \ A=\left( \begin{array}{cccc} 0&\lambda_1&0&0\\ \lambda_0& 0&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)\ \ \ \ \lambda_0\lambda_1\lambda_2=\lambda_3^3, \ \ \lambda_0\lambda_1\lambda_2\lambda_3=-1\,. \end{align*} $$
We will first consider Case I. In this case, combining the two equations for the
![]() $\lambda _i$
, we see that
$\lambda _i$
, we see that
![]() $\lambda _3^4=1$
. Now, let us further subdivide Case I by the order
$\lambda _3^4=1$
. Now, let us further subdivide Case I by the order
![]() $|A|$
of A; we will denote by
$|A|$
of A; we will denote by
![]() $\zeta _n$
a primitive nth root of unity. If
$\zeta _n$
a primitive nth root of unity. If
![]() $|A|=2$
, we have (recalling that we are always assuming that A generates a subgroup of
$|A|=2$
, we have (recalling that we are always assuming that A generates a subgroup of
![]() $\operatorname {PGL}(4,\mathbb {C})$
of order
$\operatorname {PGL}(4,\mathbb {C})$
of order
![]() $2$
)
$2$
)
 $$ \begin{align*}\begin{aligned} &|A|=2 \implies A=\left( \begin{array}{cccc} \pm 1& 0&0&0\\ 0&\pm 1&0&0\\ 0&0&\pm 1&0\\ 0&0&0&\pm 1 \end{array} \right)&\text{two entries } 1 \text{ and two entries } -1,\\ &|A|=4 \implies A=\left( \begin{array}{cccc} i^{i_0}& 0&0&0\\ 0&i^{i_1}&0&0\\ 0&0&i^{3i_3-i_0-i_1}&0\\ 0&0&0&i^{i_3} \end{array} \right) &\text{not all entries } i \text{ or all } -i, \text{ not all indices even},\\ &|A|=8 \implies A=\left( \begin{array}{cccc} \zeta_8^{i_0}& 0&0&0\\ 0&\zeta_8^{i_1}&0&0\\ 0&0&\zeta_8^{6i_3-i_0-i_1}&0\\ 0&0&0&\zeta_8^{2i_3} \end{array} \right)&i_0 \text{ and } i_1 \text{ not both even}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} &|A|=2 \implies A=\left( \begin{array}{cccc} \pm 1& 0&0&0\\ 0&\pm 1&0&0\\ 0&0&\pm 1&0\\ 0&0&0&\pm 1 \end{array} \right)&\text{two entries } 1 \text{ and two entries } -1,\\ &|A|=4 \implies A=\left( \begin{array}{cccc} i^{i_0}& 0&0&0\\ 0&i^{i_1}&0&0\\ 0&0&i^{3i_3-i_0-i_1}&0\\ 0&0&0&i^{i_3} \end{array} \right) &\text{not all entries } i \text{ or all } -i, \text{ not all indices even},\\ &|A|=8 \implies A=\left( \begin{array}{cccc} \zeta_8^{i_0}& 0&0&0\\ 0&\zeta_8^{i_1}&0&0\\ 0&0&\zeta_8^{6i_3-i_0-i_1}&0\\ 0&0&0&\zeta_8^{2i_3} \end{array} \right)&i_0 \text{ and } i_1 \text{ not both even}. \end{aligned} \end{align*} $$
In Case II, combining the two equations for the
![]() $\lambda _i$
, we see that
$\lambda _i$
, we see that
![]() $\lambda _3^4=-1$
, so that
$\lambda _3^4=-1$
, so that
![]() $\lambda _3$
must be a primitive
$\lambda _3$
must be a primitive
![]() $8$
th root of unity. Consequently, we can rule out the cases
$8$
th root of unity. Consequently, we can rule out the cases
![]() $|A|=2$
and
$|A|=2$
and
![]() $|A|=4$
, since then
$|A|=4$
, since then
![]() $\lambda _3^4=1$
. Thus, we must have
$\lambda _3^4=1$
. Thus, we must have
![]() $|A|=8$
, and we start by observing
$|A|=8$
, and we start by observing
 $$ \begin{align*}\left( \begin{array}{cccc} 0&\lambda_1&0&0\\ \lambda_0& 0&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)\cdot\left( \begin{array}{cccc} 0&\lambda_1&0&0\\ \lambda_0& 0&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)=\left( \begin{array}{cccc} \lambda_0\lambda_1& 0&0&0\\ 0&\lambda_0\lambda_1&0&0\\ 0&0&\lambda_2^2&0\\ 0&0&0&\lambda_3^2 \end{array} \right)\,. \end{align*} $$
$$ \begin{align*}\left( \begin{array}{cccc} 0&\lambda_1&0&0\\ \lambda_0& 0&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)\cdot\left( \begin{array}{cccc} 0&\lambda_1&0&0\\ \lambda_0& 0&0&0\\ 0&0&\lambda_2&0\\ 0&0&0&\lambda_3 \end{array} \right)=\left( \begin{array}{cccc} \lambda_0\lambda_1& 0&0&0\\ 0&\lambda_0\lambda_1&0&0\\ 0&0&\lambda_2^2&0\\ 0&0&0&\lambda_3^2 \end{array} \right)\,. \end{align*} $$
We know that
![]() $\lambda _3=\zeta _8$
is a primitive
$\lambda _3=\zeta _8$
is a primitive
![]() $8$
th root of unity. The above shows that
$8$
th root of unity. The above shows that
![]() $\lambda _0\lambda _1$
is a
$\lambda _0\lambda _1$
is a
![]() $4$
th root of unity, so we must have
$4$
th root of unity, so we must have
![]() $\lambda _0\lambda _1=\zeta _8^{2n}$
for some n. Combining this with
$\lambda _0\lambda _1=\zeta _8^{2n}$
for some n. Combining this with
![]() $\lambda _0\lambda _1\lambda _2=\lambda _3^3$
, we see that A must be of the form
$\lambda _0\lambda _1\lambda _2=\lambda _3^3$
, we see that A must be of the form
 $$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^{2n}/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{3-2n}&0\\ 0&0&0&\zeta_8 \end{array} \right)\,. \end{align*} $$
$$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^{2n}/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{3-2n}&0\\ 0&0&0&\zeta_8 \end{array} \right)\,. \end{align*} $$
Concretely, we have four options (recalling that we are always assuming that A generates a subgroup of
![]() $\operatorname {PGL}(4,\mathbb {C})$
of order
$\operatorname {PGL}(4,\mathbb {C})$
of order
![]() $2$
):
$2$
):
-
II(i)
 $$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ 1/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{3}&0\\ 0&0&0&\zeta_8 \end{array} \right), \end{align*} $$
$$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ 1/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{3}&0\\ 0&0&0&\zeta_8 \end{array} \right), \end{align*} $$
-
II(ii)
 $$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^2/\lambda_0& 0&0&0\\ 0&0&\zeta_8&0\\ 0&0&0&\zeta_8 \end{array} \right), \end{align*} $$
$$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^2/\lambda_0& 0&0&0\\ 0&0&\zeta_8&0\\ 0&0&0&\zeta_8 \end{array} \right), \end{align*} $$
-
II(iii)
 $$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^4/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{-1}&0\\ 0&0&0&\zeta_8 \end{array} \right), \end{align*} $$
$$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^4/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{-1}&0\\ 0&0&0&\zeta_8 \end{array} \right), \end{align*} $$
-
II(iv)
 $$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^6/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{-3}&0\\ 0&0&0&\zeta_8 \end{array} \right). \end{align*} $$
$$ \begin{align*}A=\left( \begin{array}{cccc} 0&\lambda_0&0&0\\ \zeta_8^6/\lambda_0& 0&0&0\\ 0&0&\zeta_8^{-3}&0\\ 0&0&0&\zeta_8 \end{array} \right). \end{align*} $$
We now consider when there can be a divisor with generic point fixed by any family of the matrices above. In Case I, the matrices A form discrete families and so we must just show that each such A has fixed locus of codimension
![]() $2$
or more. This is a case-by-case analysis. We recall that the action is given by (3.18).
$2$
or more. This is a case-by-case analysis. We recall that the action is given by (3.18).
For the case
![]() $|A|=2$
, in the notation of (3.18) where the action of A is described, the last three coordinates are fixed for the action of A, and because exactly two of the
$|A|=2$
, in the notation of (3.18) where the action of A is described, the last three coordinates are fixed for the action of A, and because exactly two of the
![]() $\lambda _i/\lambda _3$
are equal to
$\lambda _i/\lambda _3$
are equal to
![]() $-1$
, we see that the fixed locus is the intersection of the two coordinate hyperplanes given by those
$-1$
, we see that the fixed locus is the intersection of the two coordinate hyperplanes given by those
![]() $\alpha _i$
being set to zero (where the
$\alpha _i$
being set to zero (where the
![]() $\alpha _i$
are the coordinates used in (3.18)), thus of codimension at least two. For the case
$\alpha _i$
are the coordinates used in (3.18)), thus of codimension at least two. For the case
![]() $|A|=4$
, we have a matrix
$|A|=4$
, we have a matrix
 $$ \begin{align*}A=\left( \begin{array}{cccc} i^{i_0}& 0&0&0\\ 0&i^{i_1}&0&0\\ 0&0&i^{3i_3-i_0-i_1}&0\\ 0&0&0&i^{i_3} \end{array} \right)\,, \end{align*} $$
$$ \begin{align*}A=\left( \begin{array}{cccc} i^{i_0}& 0&0&0\\ 0&i^{i_1}&0&0\\ 0&0&i^{3i_3-i_0-i_1}&0\\ 0&0&0&i^{i_3} \end{array} \right)\,, \end{align*} $$
where exactly two of the entries are real, and two are imaginary. Again, looking at the action, we see that the fixed locus is contained in intersections of more than two coordinate hyperplanes and we are done. The case
![]() $|A|=8$
is similar. Indeed, suppose without loss of generality that
$|A|=8$
is similar. Indeed, suppose without loss of generality that
![]() $i_0$
is odd. Then
$i_0$
is odd. Then
![]() $2i_0\not \equiv 0\quad \mod 4$
, and
$2i_0\not \equiv 0\quad \mod 4$
, and
![]() $3i_0\not \equiv 0\quad \mod 2$
, and thus since
$3i_0\not \equiv 0\quad \mod 2$
, and thus since
![]() $\lambda _3$
is a power of the fourth (not eighths) root of unity, both
$\lambda _3$
is a power of the fourth (not eighths) root of unity, both
![]() $(\lambda _0/\lambda _3)^2$
and
$(\lambda _0/\lambda _3)^2$
and
![]() $(\lambda _0/\lambda _3)^3$
are not equal to identity, so this means the fixed locus must have
$(\lambda _0/\lambda _3)^3$
are not equal to identity, so this means the fixed locus must have
![]() $\alpha _0=\alpha _{\widehat 0} =0$
. In other words, there are no divisors in the Luna slice that have a general point fixed by a matrix A in the form of Case I.
$\alpha _0=\alpha _{\widehat 0} =0$
. In other words, there are no divisors in the Luna slice that have a general point fixed by a matrix A in the form of Case I.
We now consider Case II. Recall that in this case the action (similar to (3.18)) is given by
 $$ \begin{align*}A\cdot (\alpha_0,\alpha_1,\alpha_2,\alpha_{\widehat 0} ,\alpha_{\widehat 1} ,\alpha_{\widehat 2} )=\left(\left(\frac{\lambda_1}{\lambda_3}\right)^3\alpha_1,\left(\frac{\lambda_0}{\lambda_3}\right)^3\alpha_0, \left(\frac{\lambda_2}{\lambda_3}\right)^3\alpha_2, \left(\frac{\lambda_1}{\lambda_3}\right)^2\alpha_{\widehat 1} , \left(\frac{\lambda_0}{\lambda_3}\right)^2\alpha_{\widehat 0} , \left(\frac{\lambda_2}{\lambda_3}\right)^2\alpha_{\widehat 2} \right)\,. \end{align*} $$
$$ \begin{align*}A\cdot (\alpha_0,\alpha_1,\alpha_2,\alpha_{\widehat 0} ,\alpha_{\widehat 1} ,\alpha_{\widehat 2} )=\left(\left(\frac{\lambda_1}{\lambda_3}\right)^3\alpha_1,\left(\frac{\lambda_0}{\lambda_3}\right)^3\alpha_0, \left(\frac{\lambda_2}{\lambda_3}\right)^3\alpha_2, \left(\frac{\lambda_1}{\lambda_3}\right)^2\alpha_{\widehat 1} , \left(\frac{\lambda_0}{\lambda_3}\right)^2\alpha_{\widehat 0} , \left(\frac{\lambda_2}{\lambda_3}\right)^2\alpha_{\widehat 2} \right)\,. \end{align*} $$
Now, assume that we have a general point
![]() $(\alpha _0,\dots ,\alpha _{\widehat 2} )$
of some divisor, fixed by a matrix A in one of the four subcases of Case II. We see that
$(\alpha _0,\dots ,\alpha _{\widehat 2} )$
of some divisor, fixed by a matrix A in one of the four subcases of Case II. We see that
![]() $\alpha _0=0$
if and only if
$\alpha _0=0$
if and only if
![]() $\alpha _1=0$
. Since this is codimension
$\alpha _1=0$
. Since this is codimension
![]() $2$
(and could not sweep out a divisor while moving
$2$
(and could not sweep out a divisor while moving
![]() $\lambda _0$
), we can assume that
$\lambda _0$
), we can assume that
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $\alpha _1$
are nonzero. Then, looking in the first coordinate, we have
$\alpha _1$
are nonzero. Then, looking in the first coordinate, we have
![]() $\alpha _0/\alpha _1=(\lambda _1/\lambda _3)^3$
, and in the second coordinate,
$\alpha _0/\alpha _1=(\lambda _1/\lambda _3)^3$
, and in the second coordinate,
![]() $\alpha _1/\alpha _0=(\lambda _0/\lambda _3)^3$
. Multiplying gives us
$\alpha _1/\alpha _0=(\lambda _0/\lambda _3)^3$
. Multiplying gives us
![]() $\left (\frac {\lambda _1}{\lambda _3}\cdot \frac {\lambda _0}{\lambda _3}\right )^3=1$
, so that
$\left (\frac {\lambda _1}{\lambda _3}\cdot \frac {\lambda _0}{\lambda _3}\right )^3=1$
, so that
![]() $(\lambda _0\lambda _1)^3=\lambda _3^6$
. Looking at the list of cases, Case II(i)–(iv), the only option is Case II(ii). Now, focusing on Case II(ii), we see that
$(\lambda _0\lambda _1)^3=\lambda _3^6$
. Looking at the list of cases, Case II(i)–(iv), the only option is Case II(ii). Now, focusing on Case II(ii), we see that
![]() $\lambda _2/\lambda _3=1$
. Note that one also sees that
$\lambda _2/\lambda _3=1$
. Note that one also sees that
![]() $\alpha _{\widehat 0} /\alpha _{\widehat 1} =(\lambda _1/\lambda _3)^2$
, and
$\alpha _{\widehat 0} /\alpha _{\widehat 1} =(\lambda _1/\lambda _3)^2$
, and
![]() $\alpha _{\widehat 1} /\alpha _{\widehat 0} =(\lambda _0/\lambda _3)^2$
, which would imply that
$\alpha _{\widehat 1} /\alpha _{\widehat 0} =(\lambda _0/\lambda _3)^2$
, which would imply that
![]() $(\lambda _0\lambda _1)^2=\lambda _3^4$
, which also holds for Case II(ii).
$(\lambda _0\lambda _1)^2=\lambda _3^4$
, which also holds for Case II(ii).
In other words, if we have a general point
![]() $(\alpha _0,\dots ,\alpha _{\widehat 2} )$
of some divisor that is fixed by a matrix A in the form of Case II, then we must be in Case II(ii), and we must have
$(\alpha _0,\dots ,\alpha _{\widehat 2} )$
of some divisor that is fixed by a matrix A in the form of Case II, then we must be in Case II(ii), and we must have
Since in Case II(ii) we have
![]() $(\lambda _1/\lambda _3)=(\lambda _0/\lambda _3)^{-1}$
, we see that the above only constitutes two conditions, and cuts out a codimension
$(\lambda _1/\lambda _3)=(\lambda _0/\lambda _3)^{-1}$
, we see that the above only constitutes two conditions, and cuts out a codimension
![]() $2$
locus. As we vary
$2$
locus. As we vary
![]() $\lambda _0$
, this indeed sweeps out a divisor.
$\lambda _0$
, this indeed sweeps out a divisor.
More precisely, consider the following divisor:
that is,
![]() $\left (\frac {\alpha _1}{\alpha _0}\right )^2 = \left (\frac {\alpha _{\widehat 1} }{\alpha _{\widehat 0} }\right )^3$
. Then the general point
$\left (\frac {\alpha _1}{\alpha _0}\right )^2 = \left (\frac {\alpha _{\widehat 1} }{\alpha _{\widehat 0} }\right )^3$
. Then the general point
![]() $(\alpha _0,\alpha _1,\alpha _2,\alpha _{\widehat 0} , \alpha _{\widehat 1} , \alpha _{\widehat 2} )$
of this divisor is stabilized by a matrix of the form
$(\alpha _0,\alpha _1,\alpha _2,\alpha _{\widehat 0} , \alpha _{\widehat 1} , \alpha _{\widehat 2} )$
of this divisor is stabilized by a matrix of the form
 $$ \begin{align*}A_{\lambda_0}=\left( \begin{array}{cccc} 0 & \lambda_0& 0& 0\\ \frac{\zeta_8^2}{\lambda_0}& 0 & 0& 0\\ 0&0&\zeta_8 & 0\\ 0&0&0&\zeta_8 \end{array} \right)\in \operatorname{Stab}(S_{3A_2})\,, \end{align*} $$
$$ \begin{align*}A_{\lambda_0}=\left( \begin{array}{cccc} 0 & \lambda_0& 0& 0\\ \frac{\zeta_8^2}{\lambda_0}& 0 & 0& 0\\ 0&0&\zeta_8 & 0\\ 0&0&0&\zeta_8 \end{array} \right)\in \operatorname{Stab}(S_{3A_2})\,, \end{align*} $$
where
![]() $\zeta _8$
is a primitive
$\zeta _8$
is a primitive
![]() $8$
th root of unity, and
$8$
th root of unity, and
![]() $\lambda _0$
is chosen so that
$\lambda _0$
is chosen so that
![]() $(\frac {\lambda _0}{\zeta _8})^2= \frac {\alpha _{\widehat 1} }{\alpha _{\widehat 0} }$
. There are two choices of
$(\frac {\lambda _0}{\zeta _8})^2= \frac {\alpha _{\widehat 1} }{\alpha _{\widehat 0} }$
. There are two choices of
![]() $\lambda _0$
, and one is also free to choose another primitive
$\lambda _0$
, and one is also free to choose another primitive
![]() $8$
th root of unity, but these matrices generate the same subgroup of
$8$
th root of unity, but these matrices generate the same subgroup of
![]() $\operatorname {Stab}(S_{3A_2})$
; note that since the cyclic group
$\operatorname {Stab}(S_{3A_2})$
; note that since the cyclic group
![]() $\langle A_{\lambda _0}\rangle $
contains the diagonal
$\langle A_{\lambda _0}\rangle $
contains the diagonal
![]() $\mu _4$
, the image of
$\mu _4$
, the image of
![]() $\langle A_{\lambda _0}\rangle $
in
$\langle A_{\lambda _0}\rangle $
in
![]() $\operatorname {PGL}(4,\mathbb {C})$
is isomorphic to
$\operatorname {PGL}(4,\mathbb {C})$
is isomorphic to
![]() $\mathbb {Z}_2$
. In other words, the generic point of the divisor above corresponds to a cubic surface with automorphism group isomorphic to
$\mathbb {Z}_2$
. In other words, the generic point of the divisor above corresponds to a cubic surface with automorphism group isomorphic to
![]() $\mathbb {Z}_2$
.
$\mathbb {Z}_2$
.
Permuting the indices, this gives three divisors of the same type. Each has degree
![]() $5$
, and is a cone through the origin, and so has multiplicity
$5$
, and is a cone through the origin, and so has multiplicity
![]() $5$
at the origin. There are no other divisors in a neighborhood of
$5$
at the origin. There are no other divisors in a neighborhood of
![]() $0$
in the Luna slice parameterizing cubic surfaces with extra automorphisms. This implies that the multiplicity of the restriction of the Eckardt divisor to the Luna slice, as a reduced variety, is
$0$
in the Luna slice parameterizing cubic surfaces with extra automorphisms. This implies that the multiplicity of the restriction of the Eckardt divisor to the Luna slice, as a reduced variety, is
![]() $15$
. This completes the proof.
$15$
. This completes the proof.
Some of the computations below will use related notation to the above. Specifically, we will perform computations in charts on the blowup
![]() $\operatorname {Bl}_0\mathbb {C}^6\to \mathbb {C}^6$
of a Luna slice as above. Recall that the blowup is embedded in
$\operatorname {Bl}_0\mathbb {C}^6\to \mathbb {C}^6$
of a Luna slice as above. Recall that the blowup is embedded in
![]() $\mathbb {C}^6\times \mathbb {P}^5$
, with coordinates
$\mathbb {C}^6\times \mathbb {P}^5$
, with coordinates
![]() $\alpha $
on the
$\alpha $
on the
![]() $\mathbb {C}^6$
and homogeneous coordinates T on the
$\mathbb {C}^6$
and homogeneous coordinates T on the
![]() $\mathbb {P}^5$
. By using the
$\mathbb {P}^5$
. By using the
![]() $S_3$
action on
$S_3$
action on
![]() $\mathbb {C}^6$
and its extension to the blowup, it will be enough to work only with two charts on
$\mathbb {C}^6$
and its extension to the blowup, it will be enough to work only with two charts on
![]() $\operatorname {Bl}_0\mathbb {C}^6$
. The first chart is the chart
$\operatorname {Bl}_0\mathbb {C}^6$
. The first chart is the chart
![]() $U_0$
where
$U_0$
where
![]() $T_0\ne 0$
, and the local coordinates in this chart are then
$T_0\ne 0$
, and the local coordinates in this chart are then
and similarly for the chart
![]() $U_{\widehat 0}$
where
$U_{\widehat 0}$
where
![]() $T_{\widehat 0}\ne 0$
.
$T_{\widehat 0}\ne 0$
.
A.3 Proof of Proposition 3.7
Let
![]() $x\in D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
be a point in the exceptional divisor. We want to compute the stabilizer
$x\in D_{3A_2}\subseteq {\mathcal {M}}^{\operatorname {K}}$
be a point in the exceptional divisor. We want to compute the stabilizer
![]() $S_x\subseteq \operatorname {Stab}(S_{3A_2})\subseteq \operatorname {SL}(4,\mathbb {C})$
, that is, the stabilizer of a point in the exceptional divisor of
$S_x\subseteq \operatorname {Stab}(S_{3A_2})\subseteq \operatorname {SL}(4,\mathbb {C})$
, that is, the stabilizer of a point in the exceptional divisor of
![]() $\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
with orbit corresponding to x. By construction, it suffices to compute the stabilizers of points in the exceptional divisor of the blowup of the Luna slice, with respect to the action of
$\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
with orbit corresponding to x. By construction, it suffices to compute the stabilizers of points in the exceptional divisor of the blowup of the Luna slice, with respect to the action of
![]() $\operatorname {Stab}(S_{3A_2})$
. Indeed, the
$\operatorname {Stab}(S_{3A_2})$
. Indeed, the
![]() $\operatorname {SL}(4,\mathbb {C})$
orbit of each point in the exceptional divisor of
$\operatorname {SL}(4,\mathbb {C})$
orbit of each point in the exceptional divisor of
![]() $\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
intersects the blowup of the Luna slice, and since the blowups are equivariant, one can check that the stabilizer for the
$\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
intersects the blowup of the Luna slice, and since the blowups are equivariant, one can check that the stabilizer for the
![]() $\operatorname {SL}(4,\mathbb {C})$
action on
$\operatorname {SL}(4,\mathbb {C})$
action on
![]() $\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
is just the stabilizer for a corresponding point on the Luna slice, with respect to the action of
$\operatorname {Bl}_{\operatorname {SL}(4,\mathbb {C}) \cdot [S_{3A_2}]}(\mathbb {P}^{19})^{ss}$
is just the stabilizer for a corresponding point on the Luna slice, with respect to the action of
![]() $\operatorname {Stab}(S_{3A_2})$
.
$\operatorname {Stab}(S_{3A_2})$
.
Therefore, we work with the six-dimensional Luna slice from Lemma 3.4. In order to obtain the Kirwan blowup, we have to blow up the Luna slice at the origin, and we denote the exceptional
![]() $\mathbb {P}^5$
by E. The group
$\mathbb {P}^5$
by E. The group
![]() $\operatorname {Stab}(S_{3A_2})$
acts on the blowup, and we have to analyze the stabilizers of the action of
$\operatorname {Stab}(S_{3A_2})$
acts on the blowup, and we have to analyze the stabilizers of the action of
![]() $\operatorname {Stab}(S_{3A_2})$
on the semi-stable locus
$\operatorname {Stab}(S_{3A_2})$
on the semi-stable locus
![]() $E^{ss}$
. For this, we recall that the connected component of
$E^{ss}$
. For this, we recall that the connected component of
![]() $\operatorname {Stab}(S_{3A_2})$
is the torus given by
$\operatorname {Stab}(S_{3A_2})$
is the torus given by
![]() $\operatorname {diag}(\lambda _1, \lambda _2, \lambda _3,1)$
with
$\operatorname {diag}(\lambda _1, \lambda _2, \lambda _3,1)$
with
![]() $\lambda _1 \lambda _2 \lambda _3=1$
. From Lemma 3.3, we have an exact sequence
$\lambda _1 \lambda _2 \lambda _3=1$
. From Lemma 3.3, we have an exact sequence
where
![]() $G(3A_2)$
is a finite group which is an extension of the form
$G(3A_2)$
is a finite group which is an extension of the form
where
![]() $S_3$
acts by permuting the coordinates
$S_3$
acts by permuting the coordinates
![]() $x_0,x_1,x_2$
. We shall now analyze the stabilizers of the action of
$x_0,x_1,x_2$
. We shall now analyze the stabilizers of the action of
![]() $\operatorname {Stab}(S_{3A_2})$
on
$\operatorname {Stab}(S_{3A_2})$
on
![]() $E^{ss}$
.
$E^{ss}$
.
(1) This claim follows from Lemma 3.5. Indeed, E is the projectivization of the Luna slice, and in Lemma 3.5 it is shown that the general point of the Luna slice has stabilizer
![]() $\mu _4$
(more precisely, it is trivial that every point of the Luna slice has stabilizer containing the diagonal
$\mu _4$
(more precisely, it is trivial that every point of the Luna slice has stabilizer containing the diagonal
![]() $\mu _4$
, and in Lemma 3.5 it is shown that there is a neighborhood of the origin so that the points with stabilizer group strictly containing
$\mu _4$
, and in Lemma 3.5 it is shown that there is a neighborhood of the origin so that the points with stabilizer group strictly containing
![]() $\mu _4$
form a divisor in this neighborhood).
$\mu _4$
form a divisor in this neighborhood).
(2) Since the order of the group
![]() $G(3A_2)$
is
$G(3A_2)$
is
![]() $2^3\cdot 3$
, which is not divisible by
$2^3\cdot 3$
, which is not divisible by
![]() $5$
, it is enough to analyze the stabilizers of the connected component
$5$
, it is enough to analyze the stabilizers of the connected component
![]() $D"\cong \mathbb {T}^2$
acting on E, with the action as given in (3.18). There the action is on the Luna slice, but of course this gives the action on the projectivized Luna slice.
$D"\cong \mathbb {T}^2$
acting on E, with the action as given in (3.18). There the action is on the Luna slice, but of course this gives the action on the projectivized Luna slice.
Since it will be convenient in the next proof in this appendix, we prefer to describe the action of the connected component
![]() $\operatorname {Stab}(S_{3A_2})^\circ =D" \cong \mathbb {T}^2$
on affine charts for the blowup of
$\operatorname {Stab}(S_{3A_2})^\circ =D" \cong \mathbb {T}^2$
on affine charts for the blowup of
![]() $\mathbb {C}^6$
at the origin. Using the
$\mathbb {C}^6$
at the origin. Using the
![]() $S_3$
symmetry, we can assume that either
$S_3$
symmetry, we can assume that either
![]() $T_0 \neq 0$
or
$T_0 \neq 0$
or
![]() $T_{\widehat 0} \neq 0$
, and thus only deal with the two charts
$T_{\widehat 0} \neq 0$
, and thus only deal with the two charts
![]() $U_0$
and
$U_0$
and
![]() $U_{\widehat 0}$
on the blowup. We shall start with the chart
$U_{\widehat 0}$
on the blowup. We shall start with the chart
![]() $U_0$
, with coordinates (A.2), and focus on the exceptional divisor
$U_0$
, with coordinates (A.2), and focus on the exceptional divisor
![]() $\alpha _0=0$
within it. In the chart
$\alpha _0=0$
within it. In the chart
![]() $U_0$
, the action (3.18) is given by
$U_0$
, the action (3.18) is given by
 $$ \begin{align} \begin{aligned} (\lambda_0,\lambda_1,\lambda_2,\lambda_3)&\cdot (\alpha_0,t_1,t_2,t_{\widehat 0} , t_{\widehat 1} , t_{\widehat 2} )=\\ &=\left(\left(\frac{\lambda_0}{\lambda_3}\right)^3\alpha_0,\left(\frac{\lambda_1}{\lambda_0}\right)^3t_1,\left(\frac{\lambda_2}{\lambda_0}\right)^3t_2, \left(\frac{\lambda_3}{\lambda_0}\right)t_{\widehat 0} , \left(\frac{\lambda_1^2\lambda_3}{\lambda_0^3}\right) t_{\widehat 1} , \left(\frac{\lambda_2^2\lambda_3}{\lambda_0^3}\right)t_{\widehat 2} \right)&\quad (\mbox{for } D')\,\,\\ &=\left(\lambda_0^3\alpha_0,\lambda_0^{-3}\lambda_1^{3}t_1, \lambda_0^{-6}\lambda_1^{-3}t_2,\lambda_0^{-1}t_{\widehat 0} ,\lambda_0^{-3}\lambda_1^{2}t_{\widehat 1} , \lambda_0^{-5}\lambda_1^{-2}t_{\widehat 2} \right)& (\mbox{for } D")\,, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\lambda_0,\lambda_1,\lambda_2,\lambda_3)&\cdot (\alpha_0,t_1,t_2,t_{\widehat 0} , t_{\widehat 1} , t_{\widehat 2} )=\\ &=\left(\left(\frac{\lambda_0}{\lambda_3}\right)^3\alpha_0,\left(\frac{\lambda_1}{\lambda_0}\right)^3t_1,\left(\frac{\lambda_2}{\lambda_0}\right)^3t_2, \left(\frac{\lambda_3}{\lambda_0}\right)t_{\widehat 0} , \left(\frac{\lambda_1^2\lambda_3}{\lambda_0^3}\right) t_{\widehat 1} , \left(\frac{\lambda_2^2\lambda_3}{\lambda_0^3}\right)t_{\widehat 2} \right)&\quad (\mbox{for } D')\,\,\\ &=\left(\lambda_0^3\alpha_0,\lambda_0^{-3}\lambda_1^{3}t_1, \lambda_0^{-6}\lambda_1^{-3}t_2,\lambda_0^{-1}t_{\widehat 0} ,\lambda_0^{-3}\lambda_1^{2}t_{\widehat 1} , \lambda_0^{-5}\lambda_1^{-2}t_{\widehat 2} \right)& (\mbox{for } D")\,, \end{aligned} \end{align} $$
where in the last equality we are using that in
![]() $\operatorname {Stab}(S_{3A_2})^\circ =D" \cong \mathbb {T}^2$
we have
$\operatorname {Stab}(S_{3A_2})^\circ =D" \cong \mathbb {T}^2$
we have
![]() $\lambda _3=1$
, and
$\lambda _3=1$
, and
![]() $\lambda _2=\lambda _0^{-1}\lambda _1^{-1}$
. We note in passing that this chart for the blowup is not equivariant with respect to the full stabilizer group
$\lambda _2=\lambda _0^{-1}\lambda _1^{-1}$
. We note in passing that this chart for the blowup is not equivariant with respect to the full stabilizer group
![]() $\operatorname {Stab}(S_{3A_2})$
, as any element of
$\operatorname {Stab}(S_{3A_2})$
, as any element of
![]() $S_3$
that does not fix
$S_3$
that does not fix
![]() $0$
would not preserve it.
$0$
would not preserve it.
The proof of (1) now becomes a case-by-case check, determining the group of
![]() $(\lambda _0,\lambda _1)\subseteq \mathbb {T}^2$
that stabilizes a given point on the exceptional divisor, that is, with coordinate
$(\lambda _0,\lambda _1)\subseteq \mathbb {T}^2$
that stabilizes a given point on the exceptional divisor, that is, with coordinate
![]() $\alpha _0=0$
. Recall that Lemma 3.6 described the unstable locus on this exceptional divisor, and we are only interested in semi-stable (which are in fact all stable, as this is the Kirwan blowup) orbits.
$\alpha _0=0$
. Recall that Lemma 3.6 described the unstable locus on this exceptional divisor, and we are only interested in semi-stable (which are in fact all stable, as this is the Kirwan blowup) orbits.
First, we consider the locus where
![]() $t_{\widehat 0}\ne 0$
. Such a point can only be stabilized if
$t_{\widehat 0}\ne 0$
. Such a point can only be stabilized if
![]() $\lambda _0^{-1}=1$
. If all four coordinates
$\lambda _0^{-1}=1$
. If all four coordinates
![]() $t_1,t_2,t_{\widehat 1},t_{\widehat 2}$
are nonzero, then the stabilizer is trivial. If
$t_1,t_2,t_{\widehat 1},t_{\widehat 2}$
are nonzero, then the stabilizer is trivial. If
![]() $t_1=t_2=0$
, then stabilizer consists of
$t_1=t_2=0$
, then stabilizer consists of
![]() $\lambda _1$
such that
$\lambda _1$
such that
![]() $\lambda _1^2=\lambda _1^{-2}=1$
, that is, is the group
$\lambda _1^2=\lambda _1^{-2}=1$
, that is, is the group
![]() $\mathbb {Z}_2$
. If
$\mathbb {Z}_2$
. If
![]() $t_{\widehat 1}=t_{\widehat 2}=0$
, then the stabilizer is
$t_{\widehat 1}=t_{\widehat 2}=0$
, then the stabilizer is
![]() $\mathbb {Z}_3$
.
$\mathbb {Z}_3$
.
We now deal with the points where the coordinate
![]() $t_{\widehat 0}=0$
. For such a point to be stable, Lemma 3.6 implies that one of the following pairs of coordinates must both be nonzero:
$t_{\widehat 0}=0$
. For such a point to be stable, Lemma 3.6 implies that one of the following pairs of coordinates must both be nonzero:
![]() $(t_1,t_2)$
,
$(t_1,t_2)$
,
![]() $(t_1,t_{\widehat 2})$
,
$(t_1,t_{\widehat 2})$
,
![]() $(t_{\widehat 1},t_2)$
, or
$(t_{\widehat 1},t_2)$
, or
![]() $(t_{\widehat 1},t_{\widehat 2})$
. For any pair of nonzero coordinates, the action of
$(t_{\widehat 1},t_{\widehat 2})$
. For any pair of nonzero coordinates, the action of
![]() $\mathbb {T}^2$
on this pair of coordinates is given by multiplying them by
$\mathbb {T}^2$
on this pair of coordinates is given by multiplying them by
![]() $(\lambda _0^a\lambda _1^b,\lambda _0^c\lambda _1^d)$
. If
$(\lambda _0^a\lambda _1^b,\lambda _0^c\lambda _1^d)$
. If
![]() $t_1t_2\ne 0=t_{\widehat 1}=t_{\widehat 2}$
, then the stabilizer must satisfy
$t_1t_2\ne 0=t_{\widehat 1}=t_{\widehat 2}$
, then the stabilizer must satisfy
![]() $\lambda _0^{-3}\lambda _1^3=1$
and
$\lambda _0^{-3}\lambda _1^3=1$
and
![]() $\lambda _0^{-6}\lambda _1^{-3}=1$
. Thus,
$\lambda _0^{-6}\lambda _1^{-3}=1$
. Thus,
![]() $\lambda _0=\lambda _1\rho $
from the first equation, for
$\lambda _0=\lambda _1\rho $
from the first equation, for
![]() $\rho $
a third root of unity, and then the second equation gives
$\rho $
a third root of unity, and then the second equation gives
![]() $\lambda _1^{-6}\lambda _1^{-3}=1$
, so that
$\lambda _1^{-6}\lambda _1^{-3}=1$
, so that
![]() $\lambda _1$
can then be an arbitrary ninth root of unity. Altogether the stabilizer group is then
$\lambda _1$
can then be an arbitrary ninth root of unity. Altogether the stabilizer group is then
![]() $\mathbb {Z}_3\times \mathbb {Z}_9$
.
$\mathbb {Z}_3\times \mathbb {Z}_9$
.
For the other three cases, the powers
![]() $(a,b)$
and
$(a,b)$
and
![]() $(c,d)$
are linearly independent, and at least one of them is a primitive integral vector. Thus, in each of these cases, the stabilizer of the pair where these are the only two coordinates is a cyclic group of order
$(c,d)$
are linearly independent, and at least one of them is a primitive integral vector. Thus, in each of these cases, the stabilizer of the pair where these are the only two coordinates is a cyclic group of order
![]() $|ad-bc|$
. For
$|ad-bc|$
. For
![]() $t_1t_{\widehat 2} \neq 0=t_2=t_{\widehat 1}$
, the powers are
$t_1t_{\widehat 2} \neq 0=t_2=t_{\widehat 1}$
, the powers are
![]() $(-3,3)$
and
$(-3,3)$
and
![]() $(-5,-2)$
, and thus we obtain
$(-5,-2)$
, and thus we obtain
![]() $\mathbb {Z}_{21}$
. For
$\mathbb {Z}_{21}$
. For
![]() $t_{\widehat 1} t_2\ne 0=t_1=t_{\widehat 2}$
, the powers are
$t_{\widehat 1} t_2\ne 0=t_1=t_{\widehat 2}$
, the powers are
![]() $(-6,-3)$
and
$(-6,-3)$
and
![]() $(-3,2)$
, and thus we again obtain
$(-3,2)$
, and thus we again obtain
![]() $\mathbb {Z}_{21}$
(as we should, since the coordinate interchange
$\mathbb {Z}_{21}$
(as we should, since the coordinate interchange
![]() $(t_1,t_{\widehat 1})\leftrightarrow (t_{\widehat 1},t_{\widehat 2})$
interchanges this with the previous case). Finally, for
$(t_1,t_{\widehat 1})\leftrightarrow (t_{\widehat 1},t_{\widehat 2})$
interchanges this with the previous case). Finally, for
![]() $t_{\widehat 1} t_{\widehat 2}\ne 0=t_1=t_2$
, the powers are
$t_{\widehat 1} t_{\widehat 2}\ne 0=t_1=t_2$
, the powers are
![]() $(-3,2)$
and
$(-3,2)$
and
![]() $(-5,-2)$
, and thus we obtain
$(-5,-2)$
, and thus we obtain
![]() $\mathbb {Z}_{16}$
. The stabilizers for any case where more than two of the coordinates are nonzero is a subgroup of one of these listed groups, and thus also has order not divisible by 5.
$\mathbb {Z}_{16}$
. The stabilizers for any case where more than two of the coordinates are nonzero is a subgroup of one of these listed groups, and thus also has order not divisible by 5.
It remains to consider the chart
![]() $U_{\widehat 0}$
where
$U_{\widehat 0}$
where
![]() $T_{\widehat 0} \ne 0$
, so that the coordinates on this chart are
$T_{\widehat 0} \ne 0$
, so that the coordinates on this chart are
![]() $(t_0,t_1,t_2,\alpha _{\widehat 0},t_{\widehat 1},t_{\widehat 2})$
with
$(t_0,t_1,t_2,\alpha _{\widehat 0},t_{\widehat 1},t_{\widehat 2})$
with
![]() $\alpha _i=t_i\alpha _{\widehat 0}$
. Writing down the action (3.18) in these coordinates gives
$\alpha _i=t_i\alpha _{\widehat 0}$
. Writing down the action (3.18) in these coordinates gives
 $$ \begin{align} \begin{aligned} (\lambda_0,\lambda_1,\lambda_2,\lambda_3)&\cdot (t_0,t_1,t_2,\alpha_{\widehat 0} ,t_{\widehat 1} ,t_{\widehat 2} )=\\ &=\left(\tfrac{\lambda_0}{\lambda_3}t_0,\tfrac{\lambda_1^3}{\lambda_0^2\lambda_3}t_1, \tfrac{\lambda_2^3}{\lambda_0^2\lambda_3}t_2,\tfrac{\lambda_0^2}{\lambda_3^2}\alpha_{\widehat 0}, \tfrac{\lambda_1^2}{\lambda_0^2}t_{\widehat 1} , \tfrac{\lambda_2^2}{\lambda_0^2}t_{\widehat 2} \right)&\quad (\mbox{for } D')\,\,\\ &=\left(\lambda_0 t_0,\lambda_0^{-2}\lambda_1^{3}t_1,\lambda_0^{-5}\lambda_1^{-3}t_2,\lambda_0^2\alpha_{\widehat 0} ,\lambda_0^{-2}\lambda_1^{2}t_{\widehat 1} , \lambda_0^{-4}\lambda_1^{-2}t_{\widehat 2} \right)&\quad(\mbox{for } D")\,. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (\lambda_0,\lambda_1,\lambda_2,\lambda_3)&\cdot (t_0,t_1,t_2,\alpha_{\widehat 0} ,t_{\widehat 1} ,t_{\widehat 2} )=\\ &=\left(\tfrac{\lambda_0}{\lambda_3}t_0,\tfrac{\lambda_1^3}{\lambda_0^2\lambda_3}t_1, \tfrac{\lambda_2^3}{\lambda_0^2\lambda_3}t_2,\tfrac{\lambda_0^2}{\lambda_3^2}\alpha_{\widehat 0}, \tfrac{\lambda_1^2}{\lambda_0^2}t_{\widehat 1} , \tfrac{\lambda_2^2}{\lambda_0^2}t_{\widehat 2} \right)&\quad (\mbox{for } D')\,\,\\ &=\left(\lambda_0 t_0,\lambda_0^{-2}\lambda_1^{3}t_1,\lambda_0^{-5}\lambda_1^{-3}t_2,\lambda_0^2\alpha_{\widehat 0} ,\lambda_0^{-2}\lambda_1^{2}t_{\widehat 1} , \lambda_0^{-4}\lambda_1^{-2}t_{\widehat 2} \right)&\quad(\mbox{for } D")\,. \end{aligned} \end{align} $$
The only points in the exceptional divisor in the chart
![]() $U_{\widehat 0}$
whose
$U_{\widehat 0}$
whose
![]() $S_3$
orbit is disjoint from the chart
$S_3$
orbit is disjoint from the chart
![]() $U_0$
are those where
$U_0$
are those where
![]() $t_0=t_1=t_2=0$
. For such a point to be stable, we must then have
$t_0=t_1=t_2=0$
. For such a point to be stable, we must then have
![]() $t_{\widehat 1} t_{\widehat 2}\ne 0$
. In this case, the action is by
$t_{\widehat 1} t_{\widehat 2}\ne 0$
. In this case, the action is by
![]() $\lambda _0^{-2}\lambda _1^2$
and
$\lambda _0^{-2}\lambda _1^2$
and
![]() $\lambda _0^{-4}\lambda _1^{-2}$
. From
$\lambda _0^{-4}\lambda _1^{-2}$
. From
![]() $\lambda _0^{-2}\lambda _1^2=1$
, it then follows that
$\lambda _0^{-2}\lambda _1^2=1$
, it then follows that
![]() $\lambda _0=\lambda _1\sigma $
for some
$\lambda _0=\lambda _1\sigma $
for some
![]() $\sigma \in \pm 1$
, and then from the second equation
$\sigma \in \pm 1$
, and then from the second equation
![]() $\lambda _1$
is a 6th root of unity, so we obtain the stabilizer
$\lambda _1$
is a 6th root of unity, so we obtain the stabilizer
![]() $\mathbb {Z}_2\times \mathbb {Z}_6$
.
$\mathbb {Z}_2\times \mathbb {Z}_6$
.
A.4 Proof of Proposition 3.9
We will work in the Luna slice identified in Lemma 3.4, with the action of the toric part of the stabilizer on the affine space
![]() $\mathbb {C}^6$
with coordinates
$\mathbb {C}^6$
with coordinates
![]() $\alpha _0,\alpha _1,\alpha _2, \alpha _{\widehat 0} ,\alpha _{\widehat 1} ,\alpha _{\widehat 2} $
given by (3.18), and
$\alpha _0,\alpha _1,\alpha _2, \alpha _{\widehat 0} ,\alpha _{\widehat 1} ,\alpha _{\widehat 2} $
given by (3.18), and
![]() $S_3$
permuting pairs of coordinates with the same index.
$S_3$
permuting pairs of coordinates with the same index.
We first claim that in this Luna slice, the discriminant divisor
![]() $D_{A_1}$
locally near the origin is given by the equation
$D_{A_1}$
locally near the origin is given by the equation
More precisely, it is known [Reference Dolgachev and DuncandPW] that the global deformations of the
![]() $3A_2$
cubic surfaces versally (and independently) unfold the three
$3A_2$
cubic surfaces versally (and independently) unfold the three
![]() $A_2$
singularities (i.e., the global-to-local restriction of deformations is surjective). Since the Luna slice is smooth of dimension
$A_2$
singularities (i.e., the global-to-local restriction of deformations is surjective). Since the Luna slice is smooth of dimension
![]() $6$
, it follows that locally analytically (or étale locally) the Luna slice is just a product of three copies of the standard deformation space for the
$6$
, it follows that locally analytically (or étale locally) the Luna slice is just a product of three copies of the standard deformation space for the
![]() $A_2$
singularity (see, e.g., [Reference Casalaina-Martin and LazaCMG+2, §3.4, esp. Fact 3.13]). In particular, it follows that the divisor
$A_2$
singularity (see, e.g., [Reference Casalaina-Martin and LazaCMG+2, §3.4, esp. Fact 3.13]). In particular, it follows that the divisor
![]() $D_{A_1}$
in the Luna slice is locally the union of three (divisorial) components, and we denote it
$D_{A_1}$
in the Luna slice is locally the union of three (divisorial) components, and we denote it
![]() , with
, with
![]() $S_3$
permuting the components. This shows that locally analytically there are some coordinates for the Luna slice so that (A.7) is the equation of the discriminant. We claim that (A.7) is in fact the local equation of the discriminant in our given coordinates from Lemma 3.4. By the discussion above, it suffices to show that the hypersurface in the Luna slice given by the equation
$S_3$
permuting the components. This shows that locally analytically there are some coordinates for the Luna slice so that (A.7) is the equation of the discriminant. We claim that (A.7) is in fact the local equation of the discriminant in our given coordinates from Lemma 3.4. By the discussion above, it suffices to show that the hypersurface in the Luna slice given by the equation
![]() $27\alpha _0^2+4\alpha _{\widehat 0} ^3=0$
in our coordinates is contained in the discriminant. Taking partial derivatives of our family of cubics parameterized by the Luna slice in Lemma 3.4
$27\alpha _0^2+4\alpha _{\widehat 0} ^3=0$
in our coordinates is contained in the discriminant. Taking partial derivatives of our family of cubics parameterized by the Luna slice in Lemma 3.4
one can check that if
![]() $27\alpha _0^2+4\alpha _{\widehat 0} ^3=0$
, then the associated cubic has a singularity at the point
$27\alpha _0^2+4\alpha _{\widehat 0} ^3=0$
, then the associated cubic has a singularity at the point
![]() $(1:0:0:-\tfrac {3\alpha _0}{2\alpha _{\widehat 0}})$
, unless
$(1:0:0:-\tfrac {3\alpha _0}{2\alpha _{\widehat 0}})$
, unless
![]() $\alpha _{\widehat 0}=0$
, in which case
$\alpha _{\widehat 0}=0$
, in which case
![]() $\alpha _0=0$
, and the associated cubic has a singularity at
$\alpha _0=0$
, and the associated cubic has a singularity at
![]() $(1:0:0:0)$
, establishing the claim.
$(1:0:0:0)$
, establishing the claim.
The Kirwan desingularization proceeds by blowing up the origin of this Luna slice
![]() $\mathbb {C}^6$
, and then taking the GIT quotient of the blowup by the stabilizer
$\mathbb {C}^6$
, and then taking the GIT quotient of the blowup by the stabilizer
![]() $\operatorname {Stab}(S_{3A_2})$
given by (3.11). We will determine the strict transform of H in the coordinate charts on the blowup
$\operatorname {Stab}(S_{3A_2})$
given by (3.11). We will determine the strict transform of H in the coordinate charts on the blowup
![]() $\operatorname {Bl}_0\mathbb {C}^6\subseteq \mathbb {C}^6\times \mathbb {P}^5$
. As in the previous proof, by symmetry it is enough to work in the chart
$\operatorname {Bl}_0\mathbb {C}^6\subseteq \mathbb {C}^6\times \mathbb {P}^5$
. As in the previous proof, by symmetry it is enough to work in the chart
![]() $U_0$
given by (A.2), and in the chart
$U_0$
given by (A.2), and in the chart
![]() $U_{\widehat 0} $
where
$U_{\widehat 0} $
where
![]() $t_{\widehat 0} \ne 0$
.
$t_{\widehat 0} \ne 0$
.
We start with the chart
![]() $U_0$
, and use (A.2) to express the proper transform of the divisor H on it as
$U_0$
, and use (A.2) to express the proper transform of the divisor H on it as
In this chart, the exceptional divisor of the blowup is given by
![]() $\alpha _0=0$
, and thus the strict transform of the divisor H just omits the
$\alpha _0=0$
, and thus the strict transform of the divisor H just omits the
![]() $\alpha _0^6$
factor above. To compute the local structure of the Kirwan blowup, we now need the Luna slice for the action of the torus
$\alpha _0^6$
factor above. To compute the local structure of the Kirwan blowup, we now need the Luna slice for the action of the torus
![]() $\mathbb {T}^2\subseteq \operatorname {Stab}(S_{3A_2})$
given by diagonal matrices with
$\mathbb {T}^2\subseteq \operatorname {Stab}(S_{3A_2})$
given by diagonal matrices with
![]() $\lambda _0\lambda _1\lambda _2=1=\lambda _3$
in the chart
$\lambda _0\lambda _1\lambda _2=1=\lambda _3$
in the chart
![]() $U_0$
, which is given in (A.5). One can check directly that the
$U_0$
, which is given in (A.5). One can check directly that the
![]() $\mathbb {C}^4$
given by the two equations
$\mathbb {C}^4$
given by the two equations
![]() $t_1=t_{\widehat 1} =1$
is the Luna slice for the action of
$t_1=t_{\widehat 1} =1$
is the Luna slice for the action of
![]() $\mathbb {T}^2$
in this chart. Thus, the intersection of the strict transform of the divisor H with this Luna slice is given by
$\mathbb {T}^2$
in this chart. Thus, the intersection of the strict transform of the divisor H with this Luna slice is given by
which intersects the exceptional divisor
![]() $\alpha _0=0$
non-transversally. Indeed, the last factor in this strict transform intersects the exceptional divisor as the intersection of the loci
$\alpha _0=0$
non-transversally. Indeed, the last factor in this strict transform intersects the exceptional divisor as the intersection of the loci
![]() $\alpha _0=0$
and
$\alpha _0=0$
and
![]() $27 t_2^2+4\alpha _0 t_{\widehat 2} ^3=0$
, which is non-transversal: they intersect along the codimension 2 space
$27 t_2^2+4\alpha _0 t_{\widehat 2} ^3=0$
, which is non-transversal: they intersect along the codimension 2 space
![]() $\alpha _0=t_2=0$
, but with multiplicity 2. To ascertain the non-transversality in the moduli space, one needs to further check that taking the quotient by
$\alpha _0=t_2=0$
, but with multiplicity 2. To ascertain the non-transversality in the moduli space, one needs to further check that taking the quotient by
![]() $\mathbb {T}^2$
and by
$\mathbb {T}^2$
and by
![]() $S_3$
does not cause the intersection to become transverse. For completeness, and as a cross-check, we will perform this computation in full detail in the chart
$S_3$
does not cause the intersection to become transverse. For completeness, and as a cross-check, we will perform this computation in full detail in the chart
![]() $U_{\widehat 0} $
.
$U_{\widehat 0} $
.
We now work in the chart
![]() $U_{\widehat 0} $
with coordinates
$U_{\widehat 0} $
with coordinates
![]() $t_0,t_1,t_2,\alpha _{\widehat 0} ,t_{\widehat 1} ,t_{\widehat 2} $
, and express
$t_0,t_1,t_2,\alpha _{\widehat 0} ,t_{\widehat 1} ,t_{\widehat 2} $
, and express
![]() $\alpha _i=\alpha _{\widehat 0} t_i$
. Thus, the proper transform of the discriminant divisor H becomes
$\alpha _i=\alpha _{\widehat 0} t_i$
. Thus, the proper transform of the discriminant divisor H becomes
In this chart, the exceptional divisor of the blowup is given by
![]() $\alpha _{\widehat 0} =0$
, and thus the strict transform of the divisor H again just omits the
$\alpha _{\widehat 0} =0$
, and thus the strict transform of the divisor H again just omits the
![]() $\alpha _{\widehat 0} ^6$
factor. To compute the local structure of the Kirwan blowup, we need the Luna slice for the action of the torus
$\alpha _{\widehat 0} ^6$
factor. To compute the local structure of the Kirwan blowup, we need the Luna slice for the action of the torus
![]() $\mathbb {T}^2\subseteq \operatorname {Stab}(S_{3A_2})$
given by diagonal matrices with
$\mathbb {T}^2\subseteq \operatorname {Stab}(S_{3A_2})$
given by diagonal matrices with
![]() $\lambda _0\lambda _1\lambda _2=1=\lambda _3$
in the chart
$\lambda _0\lambda _1\lambda _2=1=\lambda _3$
in the chart
![]() $U_{\widehat 0} $
, where the action is given by (A.6). We claim that the
$U_{\widehat 0} $
, where the action is given by (A.6). We claim that the
![]() $\mathbb {C}^4$
given by the two equations
$\mathbb {C}^4$
given by the two equations
![]() $t_{\widehat 1} =t_{\widehat 2} =1$
is a Luna slice for this action of
$t_{\widehat 1} =t_{\widehat 2} =1$
is a Luna slice for this action of
![]() $\mathbb {T}^2$
on
$\mathbb {T}^2$
on
![]() $U_{\widehat 0} =\mathbb {C}^6$
. Indeed, for any point
$U_{\widehat 0} =\mathbb {C}^6$
. Indeed, for any point
![]() $t_0,t_1,t_2,\alpha _{\widehat 0} ,t_{\widehat 1} ,t_{\widehat 2} \in U_{\widehat 0} $
with
$t_0,t_1,t_2,\alpha _{\widehat 0} ,t_{\widehat 1} ,t_{\widehat 2} \in U_{\widehat 0} $
with
![]() $t_{\widehat 1} t_{\widehat 2} \ne 0$
, there exist
$t_{\widehat 1} t_{\widehat 2} \ne 0$
, there exist
![]() $\lambda _0,\lambda _1$
such that
$\lambda _0,\lambda _1$
such that
![]() $\lambda _0^{-2}\lambda _1^2=t_{\widehat 1}^{-1}$
and
$\lambda _0^{-2}\lambda _1^2=t_{\widehat 1}^{-1}$
and
![]() $\lambda _0^{-4}\lambda _1^{-2}=t_{\widehat 2}^{-1}$
, and thus acting by these
$\lambda _0^{-4}\lambda _1^{-2}=t_{\widehat 2}^{-1}$
, and thus acting by these
![]() $(\lambda _0,\lambda _1)$
shows that the orbit contains a point with
$(\lambda _0,\lambda _1)$
shows that the orbit contains a point with
![]() $t_{\widehat 1}=t_{\widehat 2}=1$
. The same computation also shows that the stabilizer within
$t_{\widehat 1}=t_{\widehat 2}=1$
. The same computation also shows that the stabilizer within
![]() $\mathbb {T}^2$
of any point on this
$\mathbb {T}^2$
of any point on this
![]() $\mathbb {C}^4$
slice is at most finite.
$\mathbb {C}^4$
slice is at most finite.
Restricting the strict transform of the divisor H to this Luna slice for the
![]() $\mathbb {T}^2$
gives
$\mathbb {T}^2$
gives
The intersection of the first factor with the exceptional locus
![]() $\alpha _{\widehat 0}=0$
is along the codimension two locus
$\alpha _{\widehat 0}=0$
is along the codimension two locus
![]() $t_0=\alpha _{\widehat 0} =0$
, along which the first factor intersects the exceptional divisor non-transversally (we observe that by Lemma 3.6 a generic point in the chart
$t_0=\alpha _{\widehat 0} =0$
, along which the first factor intersects the exceptional divisor non-transversally (we observe that by Lemma 3.6 a generic point in the chart
![]() $U_{\widehat 0}$
with coordinates
$U_{\widehat 0}$
with coordinates
![]() $t_0=\alpha _{\widehat 0}=0$
is stable, as indeed
$t_0=\alpha _{\widehat 0}=0$
is stable, as indeed
![]() $T_{\widehat 0}\ne 0$
).
$T_{\widehat 0}\ne 0$
).
What remains to check non-transversality is to handle the finite part of the stabilizer
![]() $\operatorname {Stab}(S_{3A_2})$
, as in principle the quotient of a non-transversal intersection by a finite group may be transversal. We will thus verify that the subgroup of
$\operatorname {Stab}(S_{3A_2})$
, as in principle the quotient of a non-transversal intersection by a finite group may be transversal. We will thus verify that the subgroup of
![]() $\operatorname {Stab}(S_{3A_2})$
that fixes a generic point of the intersection of the strict transform of H in chart
$\operatorname {Stab}(S_{3A_2})$
that fixes a generic point of the intersection of the strict transform of H in chart
![]() $U_{\widehat 0} $
with the exceptional divisor
$U_{\widehat 0} $
with the exceptional divisor
![]() $\alpha _{\widehat 0} =0$
is trivial.
$\alpha _{\widehat 0} =0$
is trivial.
Indeed, such a generic point of intersection has coordinates
![]() $(t_0=0,t_1,t_2,\alpha _{\widehat 0}=0,t_{\widehat 1} ,t_{\widehat 2} )$
, as discussed above. If an element of the group
$(t_0=0,t_1,t_2,\alpha _{\widehat 0}=0,t_{\widehat 1} ,t_{\widehat 2} )$
, as discussed above. If an element of the group
![]() $\operatorname {Stab}(S_{3A_2})$
as described in (3.11) fixes this point, then we claim that the image of this element in
$\operatorname {Stab}(S_{3A_2})$
as described in (3.11) fixes this point, then we claim that the image of this element in
![]() $S_3$
must be either the identity or the involution
$S_3$
must be either the identity or the involution
![]() $1\leftrightarrow 2$
, which permutes coordinates
$1\leftrightarrow 2$
, which permutes coordinates
![]() $(t_1,t_{\widehat 1} )\leftrightarrow (t_2,t_{\widehat 2} )$
(this statement also appears in the proof of Lemma 3.5). To see this, note that at a generic point, the only zero coordinate in
$(t_1,t_{\widehat 1} )\leftrightarrow (t_2,t_{\widehat 2} )$
(this statement also appears in the proof of Lemma 3.5). To see this, note that at a generic point, the only zero coordinate in
![]() $\mathbb {P}^5$
is
$\mathbb {P}^5$
is
![]() $t_0$
, and thus the image in
$t_0$
, and thus the image in
![]() $S_3$
of an element of a stabilizer fixing a generic point must fix
$S_3$
of an element of a stabilizer fixing a generic point must fix
![]() $0\in \lbrace 0,1,2\rbrace $
. For an element of
$0\in \lbrace 0,1,2\rbrace $
. For an element of
![]() $D'\subseteq \operatorname {Stab}(S_{3A_2})$
(so that its image in
$D'\subseteq \operatorname {Stab}(S_{3A_2})$
(so that its image in
![]() $S_3$
is the identity), the action (A.6) on the locus
$S_3$
is the identity), the action (A.6) on the locus
![]() $\alpha _{\widehat 0}=t_0=0$
restricts to
$\alpha _{\widehat 0}=t_0=0$
restricts to
If a general point
![]() $t_1,t_2,t_{\widehat 1} ,t_{\widehat 2} $
is mapped to itself, then from
$t_1,t_2,t_{\widehat 1} ,t_{\widehat 2} $
is mapped to itself, then from
![]() $t_{\widehat 1} $
coordinate being preserved it follows that
$t_{\widehat 1} $
coordinate being preserved it follows that
![]() $\lambda _1=\sigma _1\lambda _0$
for some
$\lambda _1=\sigma _1\lambda _0$
for some
![]() $\sigma _1\in \{\pm 1\}$
, and then from the preservation of
$\sigma _1\in \{\pm 1\}$
, and then from the preservation of
![]() $t_1$
coordinate it follows that
$t_1$
coordinate it follows that
![]() $\lambda _1=\lambda _3$
. Similarly from the preservation of the
$\lambda _1=\lambda _3$
. Similarly from the preservation of the
![]() $t_{\widehat 2} $
coordinate, it follows that
$t_{\widehat 2} $
coordinate, it follows that
![]() $\lambda _2=\sigma _2\lambda _0$
with
$\lambda _2=\sigma _2\lambda _0$
with
![]() $\sigma _2\in \{\pm 1\}$
, and then from the preservation of the
$\sigma _2\in \{\pm 1\}$
, and then from the preservation of the
![]() $t_2$
coordinate, it follows that
$t_2$
coordinate, it follows that
![]() $\lambda _2=\lambda _3$
. Thus, finally,
$\lambda _2=\lambda _3$
. Thus, finally,
![]() $\lambda _1=\lambda _2=\lambda _3=\sigma _1 \lambda _0$
. Furthermore, equation
$\lambda _1=\lambda _2=\lambda _3=\sigma _1 \lambda _0$
. Furthermore, equation
![]() $\lambda _0\lambda _1\lambda _2=\lambda _3^3$
in the description of
$\lambda _0\lambda _1\lambda _2=\lambda _3^3$
in the description of
![]() $\operatorname {Stab}(S_{3A_2})$
in (3.11) gives
$\operatorname {Stab}(S_{3A_2})$
in (3.11) gives
![]() $\sigma _1=1$
, so that finally
$\sigma _1=1$
, so that finally
![]() $\lambda _0=\lambda _1=\lambda _2=\lambda _3$
, and since the matrix is in
$\lambda _0=\lambda _1=\lambda _2=\lambda _3$
, and since the matrix is in
![]() $\operatorname {SL}(4,\mathbb {C})$
, they must all be equal to the same fourth root of unity, so that as an element of
$\operatorname {SL}(4,\mathbb {C})$
, they must all be equal to the same fourth root of unity, so that as an element of
![]() $\operatorname {PGL}(4,\mathbb {C})$
the matrix is equal to the identity.
$\operatorname {PGL}(4,\mathbb {C})$
the matrix is equal to the identity.
Finally, for an element of
![]() $\operatorname {Stab}(S_{3A_2})$
whose image in
$\operatorname {Stab}(S_{3A_2})$
whose image in
![]() $S_3$
is the involution
$S_3$
is the involution
![]() $1\leftrightarrow 2$
, the action is
$1\leftrightarrow 2$
, the action is
If this action preserves a point, then from the coordinate
![]() $t_{\widehat 1} $
being preserved we see that
$t_{\widehat 1} $
being preserved we see that
![]() $\lambda _2^2t_{\widehat 2} =\lambda _0^2 t_{\widehat 1} $
. Fix a square root
$\lambda _2^2t_{\widehat 2} =\lambda _0^2 t_{\widehat 1} $
. Fix a square root
![]() $x=(t_{\widehat 1} /t_{\widehat 2} )^{1/2}$
, so that then
$x=(t_{\widehat 1} /t_{\widehat 2} )^{1/2}$
, so that then
![]() $\lambda _2=\sigma _2\lambda _0 x$
for some
$\lambda _2=\sigma _2\lambda _0 x$
for some
![]() $\sigma _2\in \{\pm 1\}$
. From the coordinate
$\sigma _2\in \{\pm 1\}$
. From the coordinate
![]() $t_{\widehat 2} $
being preserved, we obtain
$t_{\widehat 2} $
being preserved, we obtain
![]() $\lambda _1^2\lambda _0^{-2}t_{\widehat 1} =t_{\widehat 2} $
and thus we see that
$\lambda _1^2\lambda _0^{-2}t_{\widehat 1} =t_{\widehat 2} $
and thus we see that
![]() $\lambda _1=\sigma _1\lambda _0 x^{-1}$
for some
$\lambda _1=\sigma _1\lambda _0 x^{-1}$
for some
![]() $\sigma _1\in \{\pm 1\}$
. From the product of coordinates
$\sigma _1\in \{\pm 1\}$
. From the product of coordinates
![]() $t_1t_2$
being preserved, we see that
$t_1t_2$
being preserved, we see that
![]() $\lambda _2^3\lambda _1^3\lambda _0^{-4}\lambda _3^{-2}=1$
. Substituting here our expressions for
$\lambda _2^3\lambda _1^3\lambda _0^{-4}\lambda _3^{-2}=1$
. Substituting here our expressions for
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
yields
$\lambda _2$
yields
![]() $\sigma _1\sigma _2\lambda _0^2=\lambda _3^2$
, so that
$\sigma _1\sigma _2\lambda _0^2=\lambda _3^2$
, so that
![]() $\lambda _3=\gamma _3\lambda _0$
with
$\lambda _3=\gamma _3\lambda _0$
with
![]() $\gamma _3^2=\sigma _1\sigma _2$
. Furthermore substituting the expressions for all
$\gamma _3^2=\sigma _1\sigma _2$
. Furthermore substituting the expressions for all
![]() $\lambda $
’s in terms of
$\lambda $
’s in terms of
![]() $\lambda _0$
in the condition
$\lambda _0$
in the condition
![]() $\lambda _0\lambda _1\lambda _2=\lambda _3^3$
yields then
$\lambda _0\lambda _1\lambda _2=\lambda _3^3$
yields then
![]() $\sigma _1\sigma _2=\gamma _3^3=\sigma _1\sigma _2\gamma _3$
, so that
$\sigma _1\sigma _2=\gamma _3^3=\sigma _1\sigma _2\gamma _3$
, so that
![]() $\gamma _3=1$
and thus
$\gamma _3=1$
and thus
![]() $\sigma _1\sigma _2=1$
. Finally, computing the determinant, the condition for the matrix to lie in
$\sigma _1\sigma _2=1$
. Finally, computing the determinant, the condition for the matrix to lie in
![]() $\operatorname {SL}(4,\mathbb {C})$
gives
$\operatorname {SL}(4,\mathbb {C})$
gives
![]() $\lambda _0\lambda _1\lambda _2\lambda _3=\lambda _0^4(\sigma _1\sigma _2)=-1$
. (Note that this is indeed a minus, as the matrix is not diagonal, but includes a transposition! Recall furthermore that we are thinking about the action of
$\lambda _0\lambda _1\lambda _2\lambda _3=\lambda _0^4(\sigma _1\sigma _2)=-1$
. (Note that this is indeed a minus, as the matrix is not diagonal, but includes a transposition! Recall furthermore that we are thinking about the action of
![]() $S_3$
, and the involution
$S_3$
, and the involution
![]() $1\leftrightarrow 2$
interchanges two pairs of coordinates,
$1\leftrightarrow 2$
interchanges two pairs of coordinates,
![]() $t_1 \leftrightarrow t_2$
and
$t_1 \leftrightarrow t_2$
and
![]() $t_{\widehat 1} \leftrightarrow t_{\widehat 2}$
.) Thus, finally,
$t_{\widehat 1} \leftrightarrow t_{\widehat 2}$
.) Thus, finally,
![]() $\lambda _0=\lambda _3$
must be some eighth roots of unity, but in this case
$\lambda _0=\lambda _3$
must be some eighth roots of unity, but in this case
![]() $t_1$
is mapped to some eighth root of unity times
$t_1$
is mapped to some eighth root of unity times
![]() $x^3$
times
$x^3$
times
![]() $t_2$
. Since
$t_2$
. Since
![]() $t_1,t_2,t_{\widehat 1} ,t_{\widehat 2} $
, and thus also x, were general,
$t_1,t_2,t_{\widehat 1} ,t_{\widehat 2} $
, and thus also x, were general,
![]() $t_1$
cannot be equal to such a product, and thus there is no stabilizer of this form.
$t_1$
cannot be equal to such a product, and thus there is no stabilizer of this form.
Acknowledgments
We thank Dan Abramovich for asking about the K-equivalence of the moduli spaces. We are grateful to Damiano Fulghesu for a conversation on equivariant Chow rings. We thank John Christian Ottem for asking about the
![]() $\mathbb {L}$
-equivalence of the compactifications
$\mathbb {L}$
-equivalence of the compactifications
![]() ${\mathcal {M}}^{\operatorname {K}}$
and
${\mathcal {M}}^{\operatorname {K}}$
and
![]() ${\overline {\mathcal {B}_4/\Gamma }}$
. We are grateful to David Rydh for discussions and explanations regarding the Kirwan desingularization as a blowup of an Artin stack, which helped to clarify our thinking and to Daniel Allcock for answering questions on the ball quotient picture. Our thanks also go to Bert van Geemen who helped us clear up a question concerning the ring of invariants. We also thank Mathieu Dutour Sikiric for a computation with polytopes. S. Grushevsky thanks the Weizmann Institute of Science for its hospitality in spring 2022 when this paper was finished.
${\overline {\mathcal {B}_4/\Gamma }}$
. We are grateful to David Rydh for discussions and explanations regarding the Kirwan desingularization as a blowup of an Artin stack, which helped to clarify our thinking and to Daniel Allcock for answering questions on the ball quotient picture. Our thanks also go to Bert van Geemen who helped us clear up a question concerning the ring of invariants. We also thank Mathieu Dutour Sikiric for a computation with polytopes. S. Grushevsky thanks the Weizmann Institute of Science for its hospitality in spring 2022 when this paper was finished.