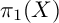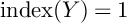0 Introduction/Main results
This paper is motivated by the p-adic analog of the anabelian Grothendieck section conjecture.
Let
![]() $p\ge 2$
be a prime number, let
$p\ge 2$
be a prime number, let
![]() $k/\mathbb {Q}_p$
be a finite extension, and let Y be a proper, smooth, and geometrically connected hyperbolic k-curve. The arithmetic fundamental group
$k/\mathbb {Q}_p$
be a finite extension, and let Y be a proper, smooth, and geometrically connected hyperbolic k-curve. The arithmetic fundamental group
![]() $\pi _1(Y)$
of Y projects onto the Galois group
$\pi _1(Y)$
of Y projects onto the Galois group
![]() $G_k\overset {\text {def}}= \operatorname {Gal} (\bar k/k)$
of k. A k-rational point
$G_k\overset {\text {def}}= \operatorname {Gal} (\bar k/k)$
of k. A k-rational point
![]() $x:\operatorname {Spec} k\to Y$
gives rise, by functoriality of fundamental groups, to a section
$x:\operatorname {Spec} k\to Y$
gives rise, by functoriality of fundamental groups, to a section
![]() $s_x:G_k\to \pi _1(Y)$
of the projection
$s_x:G_k\to \pi _1(Y)$
of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
. We shall refer to such a section
$\pi _1(Y)\twoheadrightarrow G_k$
. We shall refer to such a section
![]() $s_x$
as geometric.
$s_x$
as geometric.
Question A.
Is every section of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
geometric?
$\pi _1(Y)\twoheadrightarrow G_k$
geometric?
In [Reference Saïdi22, Theorem 2 in the Introduction], we established two necessary and sufficient conditions for a group-theoretic section of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
to be geometric. In [Reference Hoshi13], Hoshi constructed a group-theoretic section
$\pi _1(Y)\twoheadrightarrow G_k$
to be geometric. In [Reference Hoshi13], Hoshi constructed a group-theoretic section
![]() $G_k\to \pi _1(Y)^{(p)}$
of the projection
$G_k\to \pi _1(Y)^{(p)}$
of the projection
![]() $\pi _1(Y)^{(p)}\twoheadrightarrow G_k$
for a specific example Y, where
$\pi _1(Y)^{(p)}\twoheadrightarrow G_k$
for a specific example Y, where
![]() $\pi _1(Y)^{(p)}$
is the geometrically pro-p quotient of
$\pi _1(Y)^{(p)}$
is the geometrically pro-p quotient of
![]() $\pi _1(Y)$
, which is not geometric (i.e., does not arise from a scheme morphism
$\pi _1(Y)$
, which is not geometric (i.e., does not arise from a scheme morphism
![]() $x:\operatorname {Spec} k\to Y$
). The author is not aware of any example of a Y as above and a group-theoretic section of the projection
$x:\operatorname {Spec} k\to Y$
). The author is not aware of any example of a Y as above and a group-theoretic section of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
which is not geometric.
$\pi _1(Y)\twoheadrightarrow G_k$
which is not geometric.
Let X be either a geometrically connected affinoid subspace of
![]() $Y^{\operatorname {rig}}$
, the rigid analytic curve associated with Y, or a formal germ of Y, meaning
$Y^{\operatorname {rig}}$
, the rigid analytic curve associated with Y, or a formal germ of Y, meaning
![]() $X=\operatorname {Spec} (\hat {\mathcal {O}}_{{\mathcal {Y}},y}\otimes _{{\mathcal {O}}_k}k)$
is geometrically connected, where
$X=\operatorname {Spec} (\hat {\mathcal {O}}_{{\mathcal {Y}},y}\otimes _{{\mathcal {O}}_k}k)$
is geometrically connected, where
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}$
is the completion of the local ring
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}$
is the completion of the local ring
![]() ${\mathcal {O}}_{{\mathcal {Y}},y}$
of a model
${\mathcal {O}}_{{\mathcal {Y}},y}$
of a model
![]() ${\mathcal {Y}}$
of Y over the ring of valuation
${\mathcal {Y}}$
of Y over the ring of valuation
![]() ${\mathcal {O}}_k$
of k at a closed point
${\mathcal {O}}_k$
of k at a closed point
![]() $y\in {\mathcal {Y}}^{\operatorname {cl}}$
(cf. Notations). Let
$y\in {\mathcal {Y}}^{\operatorname {cl}}$
(cf. Notations). Let
![]() $\pi _1(X)$
be the étale fundamental group of X which sits in the exact sequence (cf. Notations)
$\pi _1(X)$
be the étale fundamental group of X which sits in the exact sequence (cf. Notations)
A section
![]() $s:G_k\to \pi _1(X)$
of the projection
$s:G_k\to \pi _1(X)$
of the projection
![]() $\pi _1(X)\twoheadrightarrow G_k$
induces a section
$\pi _1(X)\twoheadrightarrow G_k$
induces a section
![]() $s_Y:G_k\to \pi _1(Y)$
of the projection
$s_Y:G_k\to \pi _1(Y)$
of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
(cf. Notations, diagram (0.1)) which we shall refer to as a local section of the projection
$\pi _1(Y)\twoheadrightarrow G_k$
(cf. Notations, diagram (0.1)) which we shall refer to as a local section of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
. A geometric section is necessarily a local section as one easily verifies. This prompts the following question, which motivates our study in this paper of local sections of arithmetic fundamental groups of p-adic curves.
$\pi _1(Y)\twoheadrightarrow G_k$
. A geometric section is necessarily a local section as one easily verifies. This prompts the following question, which motivates our study in this paper of local sections of arithmetic fundamental groups of p-adic curves.
Question B.
Is every local section of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
geometric?
$\pi _1(Y)\twoheadrightarrow G_k$
geometric?
Motivated by Questions A and B, we investigate sections of arithmetic fundamental groups of affinoid k-curves and formal p-adic germs of curves.
Let X be either a smooth and geometrically connected k-affinoid curve or a formal p-adic germ (cf. Notations for precise definitions). Let
![]() $\pi _1(X)^{\operatorname {geo},\operatorname {ab}}$
be the maximal abelian quotient of
$\pi _1(X)^{\operatorname {geo},\operatorname {ab}}$
be the maximal abelian quotient of
![]() $\pi _1(X)^{\operatorname {geo}}$
, and let
$\pi _1(X)^{\operatorname {geo}}$
, and let
![]() $\pi _1(X)^{(\operatorname {ab})}$
be the geometrically abelian quotient of
$\pi _1(X)^{(\operatorname {ab})}$
be the geometrically abelian quotient of
![]() $\pi _1(X)$
which sits in the exact sequence
$\pi _1(X)$
which sits in the exact sequence
Similarly, let
![]() $G_X\overset {\text {def}} = \operatorname {Gal} (\overline L/L)$
be the absolute Galois group of the function field L of X (see Notations for the definition of L) which sits in the exact sequence (cf. §1)
$G_X\overset {\text {def}} = \operatorname {Gal} (\overline L/L)$
be the absolute Galois group of the function field L of X (see Notations for the definition of L) which sits in the exact sequence (cf. §1)
Let
![]() $G_X^{\operatorname {geo},\operatorname {ab}}$
be the maximal abelian quotient of
$G_X^{\operatorname {geo},\operatorname {ab}}$
be the maximal abelian quotient of
![]() $G_X^{\operatorname {geo}}$
, and let
$G_X^{\operatorname {geo}}$
, and let
![]() $G_X^{(\operatorname {ab})}$
be the geometrically abelian quotient of
$G_X^{(\operatorname {ab})}$
be the geometrically abelian quotient of
![]() $G_X$
which sits in the exact sequence
$G_X$
which sits in the exact sequence
We have an exact sequence
where
![]() $\widetilde {\mathcal {H}}_X \overset {\text {def}} = \operatorname {Ker} [G_X^{(\operatorname {ab})}\twoheadrightarrow \pi _1(X)^{(\operatorname {ab})}]$
. In §1, we investigate the structure of the
$\widetilde {\mathcal {H}}_X \overset {\text {def}} = \operatorname {Ker} [G_X^{(\operatorname {ab})}\twoheadrightarrow \pi _1(X)^{(\operatorname {ab})}]$
. In §1, we investigate the structure of the
![]() $G_k$
-module
$G_k$
-module
![]() $\widetilde {\mathcal {H}}_X$
. We prove in Proposition 1.4 that
$\widetilde {\mathcal {H}}_X$
. We prove in Proposition 1.4 that
![]() $\widetilde {\mathcal {H}}_X$
is (canonically) isomorphic to
$\widetilde {\mathcal {H}}_X$
is (canonically) isomorphic to
![]() $\prod _{x\in X^{\operatorname {cl}}} \operatorname {Ind} _{k(x)}^k \hat {\mathbb {Z}}(1)$
where the product is over all closed points of X and
$\prod _{x\in X^{\operatorname {cl}}} \operatorname {Ind} _{k(x)}^k \hat {\mathbb {Z}}(1)$
where the product is over all closed points of X and
![]() $k(x)$
is the residue field at x.
$k(x)$
is the residue field at x.
The Galois group
![]() $G_X$
sits in an exact sequence
$G_X$
sits in an exact sequence
where
![]() ${\mathcal {H}}_X\overset {\text {def}} = \operatorname {Ker} [G_X\twoheadrightarrow \pi _1(X)]$
. Let
${\mathcal {H}}_X\overset {\text {def}} = \operatorname {Ker} [G_X\twoheadrightarrow \pi _1(X)]$
. Let
![]() ${\mathcal {H}}_X^{\operatorname {ab}}$
be the maximal abelian quotient of
${\mathcal {H}}_X^{\operatorname {ab}}$
be the maximal abelian quotient of
![]() ${\mathcal {H}}_X$
, and let
${\mathcal {H}}_X$
, and let
![]() $G_X^{(\text c-\operatorname {ab})}$
be the geometrically cuspidally abelian quotient of
$G_X^{(\text c-\operatorname {ab})}$
be the geometrically cuspidally abelian quotient of
![]() $G_X$
which sits in the exact sequence
$G_X$
which sits in the exact sequence
In §2, we investigate, in the framework of the theory of cuspidalization of sections of arithmetic fundamental groups (cf. [Reference Saïdi19], [Reference Saïdi22]), sections
![]() $s:G_k\to \pi _1(X)$
of the projection
$s:G_k\to \pi _1(X)$
of the projection
![]() $\pi _1(X)\twoheadrightarrow G_k$
. Let Y be a k-compactification of X, and let
$\pi _1(X)\twoheadrightarrow G_k$
. Let Y be a k-compactification of X, and let
![]() $s_Y:G_k\to \pi _1(Y)$
be the induced local section of the projection
$s_Y:G_k\to \pi _1(Y)$
be the induced local section of the projection
![]() $\pi _1(Y)\twoheadrightarrow G_k$
(cf. Notations for precise definitions and the diagram (0.1) therein). One of our main results is the following (cf. Theorems 2.4 and 3.1(ii)).
$\pi _1(Y)\twoheadrightarrow G_k$
(cf. Notations for precise definitions and the diagram (0.1) therein). One of our main results is the following (cf. Theorems 2.4 and 3.1(ii)).
Theorem A (Lifting of sections to cuspidally abelian Galois groups)
Let
![]() $s:G_k\to \pi _1(X)$
be a section of the projection
$s:G_k\to \pi _1(X)$
be a section of the projection
![]() $\pi _1(X)\twoheadrightarrow G_k$
. The followings hold.
$\pi _1(X)\twoheadrightarrow G_k$
. The followings hold.
(i) There exists a section
![]() $s^{\text c-\operatorname {ab}}:G_k\to G_X^{(\text c-\operatorname {ab})}$
of the projection
$s^{\text c-\operatorname {ab}}:G_k\to G_X^{(\text c-\operatorname {ab})}$
of the projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:

where the right vertical map is the natural projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(X)$
. In particular, the set of sections of the projection
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(X)$
. In particular, the set of sections of the projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
![]() ${\mathcal {H}}_X^{\operatorname {ab}}$
) a torsor under
${\mathcal {H}}_X^{\operatorname {ab}}$
) a torsor under
![]() $H^1(G_k,{\mathcal {H}}_X^{\operatorname {ab}})$
.
$H^1(G_k,{\mathcal {H}}_X^{\operatorname {ab}})$
.
(ii) Assume Y is hyperbolic. Then the section
![]() $s_Y:G_k\to \pi _1(Y)$
induced by s is uniformly orthogonal to
$s_Y:G_k\to \pi _1(Y)$
induced by s is uniformly orthogonal to
![]() $\operatorname {Pic}$
in the sense of [Reference Saïdi19, Definition 1.4.1].
$\operatorname {Pic}$
in the sense of [Reference Saïdi19, Definition 1.4.1].
The section s is uniformly orthogonal to
![]() $\operatorname {Pic}$
(as in (ii) above) means that the retraction map
$\operatorname {Pic}$
(as in (ii) above) means that the retraction map
![]() $s^{*}:H^2(\pi _1(Y),\hat {\mathbb {Z}}(1))\overset \sim \to H^2_{\operatorname {et}}(Y,\hat {\mathbb {Z}}(1))\to H^2(G_k,\hat {\mathbb {Z}}(1))$
, which is induced by the section s, annihilates the Picard part of
$s^{*}:H^2(\pi _1(Y),\hat {\mathbb {Z}}(1))\overset \sim \to H^2_{\operatorname {et}}(Y,\hat {\mathbb {Z}}(1))\to H^2(G_k,\hat {\mathbb {Z}}(1))$
, which is induced by the section s, annihilates the Picard part of
![]() $H^2_{\operatorname {et}}(Y,\hat {\mathbb {Z}}(1))$
, and similarly for every neighborhood
$H^2_{\operatorname {et}}(Y,\hat {\mathbb {Z}}(1))$
, and similarly for every neighborhood
![]() $Y'\to Y$
of the section s.
$Y'\to Y$
of the section s.
Theorem A(ii) implies that local sections of arithmetic fundamental groups of hyperbolic p-adic curves satisfy condition (i) in [Reference Saïdi22, Theorem 2 in the Introduction]. In this sense, local sections are close to being geometric. Establishing Theorem A(ii) was one of the main motivations for the author to investigate local sections of arithmetic fundamental groups of p-adic curves. Apart from local sections, and geometric sections, the author is not aware (for the time being) of any examples of group-theoretic sections of arithmetic fundamental groups of hyperbolic p-adic curves which are orthogonal to
![]() $\operatorname {Pic}$
.
$\operatorname {Pic}$
.
As a consequence of Theorem A, and an observation of Esnault and Wittenberg on geometrically abelian sections of p-adic curves, we deduce the following (cf. Theorem 2.5).
Theorem B. Assume that X admits a k-compactification Y (cf. Notations). If the projection
![]() $\pi _1(X)\twoheadrightarrow G_k$
splits, then
$\pi _1(X)\twoheadrightarrow G_k$
splits, then
![]() $\operatorname {index} (Y)=1$
.
$\operatorname {index} (Y)=1$
.
Theorem B asserts that the existence of local sections of arithmetic fundamental groups of p-adic curves implies the existence of degree
![]() $1$
rational divisors. The link between sections of geometrically abelian Galois groups and the existence of degree
$1$
rational divisors. The link between sections of geometrically abelian Galois groups and the existence of degree
![]() $1$
rational divisors has been investigated in [Reference Esnault and Wittenberg5].
$1$
rational divisors has been investigated in [Reference Esnault and Wittenberg5].
In §3, we assume that X admits a k-compactification Y (cf. Notations). Let
![]() $\Pi _Y [X]$
be the étale fundamental group which classifies finite covers
$\Pi _Y [X]$
be the étale fundamental group which classifies finite covers
![]() $Y'\to Y$
which only ramify at points of Y not in X (cf. 3.3, as well as Notations for the meaning of not in X). A section
$Y'\to Y$
which only ramify at points of Y not in X (cf. 3.3, as well as Notations for the meaning of not in X). A section
![]() $s:G_k\to \pi _1(X)$
of the projection
$s:G_k\to \pi _1(X)$
of the projection
![]() $\pi _1(X)\twoheadrightarrow G_k$
induces naturally a section
$\pi _1(X)\twoheadrightarrow G_k$
induces naturally a section
![]() $s^{\dagger }:G_k\to \Pi _Y[X]$
of the projection
$s^{\dagger }:G_k\to \Pi _Y[X]$
of the projection
![]() $\Pi _Y[ X]\twoheadrightarrow G_k$
. We say that the section s is geometric (relative to Y) if the image
$\Pi _Y[ X]\twoheadrightarrow G_k$
. We say that the section s is geometric (relative to Y) if the image
![]() $s^{\dagger }(G_k)$
is contained in a decomposition group
$s^{\dagger }(G_k)$
is contained in a decomposition group
![]() $D_x\subset \Pi _Y[X]$
associated with a rational point
$D_x\subset \Pi _Y[X]$
associated with a rational point
![]() $x\in Y(k)$
(cf. Definition 3.3.2). Further, we say that s is admissible (relative to Y) (cf. Definition 3.5.1) if for every open subgroup
$x\in Y(k)$
(cf. Definition 3.3.2). Further, we say that s is admissible (relative to Y) (cf. Definition 3.5.1) if for every open subgroup
![]() $H\subset \Pi _Y[X]$
with
$H\subset \Pi _Y[X]$
with
![]() $s^{\dagger }(G_k)\subset H$
, corresponding to (a possibly ramified) cover
$s^{\dagger }(G_k)\subset H$
, corresponding to (a possibly ramified) cover
![]() $Y'\to Y$
, the following holds. Let
$Y'\to Y$
, the following holds. Let
![]() $G_{Y'}^{(1/p^2-\operatorname {sol})}$
be the geometrically cuspidally
$G_{Y'}^{(1/p^2-\operatorname {sol})}$
be the geometrically cuspidally
![]() $1/p^2$
-solvable Galois group of
$1/p^2$
-solvable Galois group of
![]() $Y'$
: that is, the maximal quotient
$Y'$
: that is, the maximal quotient
![]() $G_{Y'}\twoheadrightarrow H\twoheadrightarrow \pi _1(Y')$
of the absolute Galois group
$G_{Y'}\twoheadrightarrow H\twoheadrightarrow \pi _1(Y')$
of the absolute Galois group
![]() $G_{Y'}$
of
$G_{Y'}$
of
![]() $Y'$
such that
$Y'$
such that
![]() $\operatorname {Ker} [H\twoheadrightarrow \pi _1(Y')]$
is abelian annihilated by
$\operatorname {Ker} [H\twoheadrightarrow \pi _1(Y')]$
is abelian annihilated by
![]() $p^2$
(cf. [Reference Saïdi22, 3.1]). There exists a section
$p^2$
(cf. [Reference Saïdi22, 3.1]). There exists a section
![]() $\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
(such a section exists unconditionally [see discussion in 3.5]) satisfying the following property:
$G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
(such a section exists unconditionally [see discussion in 3.5]) satisfying the following property:
For each open subgroup
![]() $F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
with
$F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
with
![]() $\tilde s_{Y'}(G_k)\subset F$
, corresponding to a (possibly ramified) cover
$\tilde s_{Y'}(G_k)\subset F$
, corresponding to a (possibly ramified) cover
![]() $Y"\to Y'$
with
$Y"\to Y'$
with
![]() $Y"$
geometrically connected, the class of
$Y"$
geometrically connected, the class of
![]() $\operatorname {Pic}^1_{Y"}$
in
$\operatorname {Pic}^1_{Y"}$
in
![]() $H^1(G_k,\operatorname {Pic}^0_{Y"})$
is divisible by p.
$H^1(G_k,\operatorname {Pic}^0_{Y"})$
is divisible by p.
Our main result in §3 is the following (cf. Theorem 3.5.2).
Theorem C. The section
![]() $s:G_k\to \pi _1(X)$
is geometric (relative to Y) if and only if s is admissible (relative to Y).
$s:G_k\to \pi _1(X)$
is geometric (relative to Y) if and only if s is admissible (relative to Y).
One of the key ingredients used in the proofs of the above results is the fact that
![]() $\operatorname {Pic} (X)$
is finite. In the case where X is a formal p-adic germ, this is established in [Reference Saïdi22, Proposition 5.4], as a consequence of a result of Shuji Saito (cf. [Reference Saïdi22, Proposition 5.4]). In case X is affinoid, this is proven in §4 (cf. Proposition 4.1) and may be of interest independently of the topics discussed in this paper. More precisely, we prove the following.
$\operatorname {Pic} (X)$
is finite. In the case where X is a formal p-adic germ, this is established in [Reference Saïdi22, Proposition 5.4], as a consequence of a result of Shuji Saito (cf. [Reference Saïdi22, Proposition 5.4]). In case X is affinoid, this is proven in §4 (cf. Proposition 4.1) and may be of interest independently of the topics discussed in this paper. More precisely, we prove the following.
Theorem D (Picard groups of affinoid p-adic curves)
Let k be a p-adic local field (i.e.,
![]() $k/\mathbb {Q}_p$
is a finite extension), and let
$k/\mathbb {Q}_p$
is a finite extension), and let
![]() $X=\operatorname {Sp}(A)$
be a smooth and geometrically connected k-affinoid curve. Then the Picard group
$X=\operatorname {Sp}(A)$
be a smooth and geometrically connected k-affinoid curve. Then the Picard group
![]() $\operatorname {Pic}(X)$
is finite.
$\operatorname {Pic}(X)$
is finite.
Finally, in §5, we prove (cf. Proposition 5.1) a compactification result for two-dimensional complete local p-adic rings which is used in the proofs of Propositions 1.2 and 2.2.
The results in §4 and §5 are used in this paper in §2 and §3; none of the results in §2 and §3 is used in §4 and §5.
In this paper, we worked with full arithmetic fundamental groups. Instead, one could consider a similar setting and work with geometrically pro-p arithmetic fundamental groups and Galois groups as in [Reference Saïdi22] (where one considers geometrically pro-
![]() $\Sigma $
arithmetic fundamental groups and Galois groups,
$\Sigma $
arithmetic fundamental groups and Galois groups,
![]() $\Sigma $
being a set of primes containing p). In this geometrically pro-p (pro-
$\Sigma $
being a set of primes containing p). In this geometrically pro-p (pro-
![]() $\Sigma $
) setting, one can prove analogs of Theorems A and C.
$\Sigma $
) setting, one can prove analogs of Theorems A and C.
Notations. The following notations will be used throughout this paper (unless we specify otherwise).
-
•
 $p\ge 2$
is a prime number, and k is a p-adic local field (i.e.,
$p\ge 2$
is a prime number, and k is a p-adic local field (i.e.,
 $k/\mathbb {Q}_p$
is a finite extension) with ring of valuation
$k/\mathbb {Q}_p$
is a finite extension) with ring of valuation
 ${\mathcal {O}}_k$
, uniformizer
${\mathcal {O}}_k$
, uniformizer
 $\pi $
, and residue field F. Thus, F is a finite field of characteristic p.
$\pi $
, and residue field F. Thus, F is a finite field of characteristic p. -
• A proper, smooth, and geometrically connected k-curve Y is hyperbolic if
 $\text {genus} (Y)\ge 2$
.
$\text {genus} (Y)\ge 2$
. -
• For a profinite group H, we denote by
 $H^{\operatorname {ab}}$
the maximal abelian quotient of H.
$H^{\operatorname {ab}}$
the maximal abelian quotient of H. -
• Let
be an exact sequence of profinite groups. We will refer to a continuous homomorphism
 $s:G\to H$
such that
$s:G\to H$
such that
 $\operatorname {pr} \circ s=\operatorname {id}_{G}$
as a (group-theoretic) section of the above sequence, or simply a section of the projection
$\operatorname {pr} \circ s=\operatorname {id}_{G}$
as a (group-theoretic) section of the above sequence, or simply a section of the projection
 $\operatorname {pr} : H\twoheadrightarrow G$
.
$\operatorname {pr} : H\twoheadrightarrow G$
.
-
• All scheme cohomology groups considered in this paper are étale cohomology groups.
0.1 Affinoid p-adic curves
-
•
 $X=\operatorname {Sp} A$
is a smooth and geometrically connected affinoid k-curve. On occasions, we will write, if there is no risk of confusion,
$X=\operatorname {Sp} A$
is a smooth and geometrically connected affinoid k-curve. On occasions, we will write, if there is no risk of confusion,
 $X=\operatorname {Spec} A$
for the corresponding affine k-scheme.
$X=\operatorname {Spec} A$
for the corresponding affine k-scheme. -
• One can embed X into a proper, smooth, and geometrically connected rigid analytic curve
 $Y^{\operatorname {rig}}: X\hookrightarrow Y^{\operatorname {rig}}$
so that X is an open affinoid subspace of
$Y^{\operatorname {rig}}: X\hookrightarrow Y^{\operatorname {rig}}$
so that X is an open affinoid subspace of
 $Y^{\operatorname {rig}}$
(cf. [Reference Fresnel and Matignon6, 2.6, Corollaire 2]). Write Y for the algebraization of
$Y^{\operatorname {rig}}$
(cf. [Reference Fresnel and Matignon6, 2.6, Corollaire 2]). Write Y for the algebraization of
 $Y^{\operatorname {rig}}$
via the rigid GAGA functor, which is a proper, smooth, and geometrically connected algebraic k-curve. We will refer to X as a p-adic affinoid curve (or simply an affinoid) and Y a k-compactification of X.
$Y^{\operatorname {rig}}$
via the rigid GAGA functor, which is a proper, smooth, and geometrically connected algebraic k-curve. We will refer to X as a p-adic affinoid curve (or simply an affinoid) and Y a k-compactification of X.
0.2 Formal p-adic germs
-
• A is a normal two-dimensional complete local ring containing
 ${\mathcal {O}}_k$
with maximal ideal
${\mathcal {O}}_k$
with maximal ideal
 ${\mathfrak {m}}_A$
containing
${\mathfrak {m}}_A$
containing
 $\pi $
and residue field
$\pi $
and residue field
 $F=A/{\mathfrak {m}}_A$
. Write
$F=A/{\mathfrak {m}}_A$
. Write
 $A_k\overset {\text {def}} = A\otimes _{{\mathcal {O}}_k}k=A[\frac {1}{\pi }]$
and
$A_k\overset {\text {def}} = A\otimes _{{\mathcal {O}}_k}k=A[\frac {1}{\pi }]$
and
 $X\overset {\text {def}} = \operatorname {Spec} A_k$
. We assume X is geometrically connected and refer to X as a formal p-adic germ.
$X\overset {\text {def}} = \operatorname {Spec} A_k$
. We assume X is geometrically connected and refer to X as a formal p-adic germ. -
• A (k-)compactification of
 $\operatorname {Spec} A$
is a proper and flat relative
$\operatorname {Spec} A$
is a proper and flat relative
 ${\mathcal {O}}_k$
-curve
${\mathcal {O}}_k$
-curve
 ${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_k$
with
${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_k$
with
 ${\mathcal {Y}}$
normal,
${\mathcal {Y}}$
normal,
 $Y\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} {\mathcal {O}}_k}\operatorname {Spec} k$
geometrically connected,
$Y\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} {\mathcal {O}}_k}\operatorname {Spec} k$
geometrically connected,
 $y\in {\mathcal {Y}}^{\operatorname {cl}}$
is a closed point,
$y\in {\mathcal {Y}}^{\operatorname {cl}}$
is a closed point,
 ${\mathcal {O}}_{{\mathcal {Y}},y}$
is the local ring of
${\mathcal {O}}_{{\mathcal {Y}},y}$
is the local ring of
 ${\mathcal {Y}}$
at y,
${\mathcal {Y}}$
at y,
 $\hat {\mathcal {O}}_{{\mathcal {Y}},y}$
its completion, with an isomorphism
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}$
its completion, with an isomorphism
 $\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
. We have a natural scheme morphism
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
. We have a natural scheme morphism
 $X\to Y$
. We shall refer to Y as a k-compactification of X. In §5, we prove the existence of such a compactification
$X\to Y$
. We shall refer to Y as a k-compactification of X. In §5, we prove the existence of such a compactification
 $X\to Y$
after possibly a finite extension of k (cf. Proposition 5.1).
$X\to Y$
after possibly a finite extension of k (cf. Proposition 5.1).
In what follows, X is either an affinoid p-adic curve or a formal p-adic germ.
-
• We say that X is hyperbolic if there exists a finite extension
 $k'/k$
such that
$k'/k$
such that
 $X_{k'}\overset {\text {def}} = \operatorname {Spec}(A\otimes _k k')$
(resp.
$X_{k'}\overset {\text {def}} = \operatorname {Spec}(A\otimes _k k')$
(resp.
 $X_{k'}\overset {\text {def}} = \operatorname {Sp} (A\otimes _k k')$
if X is affinoid) possesses a
$X_{k'}\overset {\text {def}} = \operatorname {Sp} (A\otimes _k k')$
if X is affinoid) possesses a
 $k'$
-compactification Y with Y hyperbolic. There exist a finite extension
$k'$
-compactification Y with Y hyperbolic. There exist a finite extension
 $k'/k$
and a finite geometric étale cover
$k'/k$
and a finite geometric étale cover
 $X'\to X_{k'}$
with
$X'\to X_{k'}$
with
 $X'$
geometrically connected and hyperbolic. This is Proposition 5.3 in case X is a formal p-adic germ and follows from [Reference Saïdi21. Theorem A] in case X is affinoid.
$X'$
geometrically connected and hyperbolic. This is Proposition 5.3 in case X is a formal p-adic germ and follows from [Reference Saïdi21. Theorem A] in case X is affinoid. -
•
 $\eta $
is a fixed choice of a geometric point of X with values in its generic point. Thus,
$\eta $
is a fixed choice of a geometric point of X with values in its generic point. Thus,
 $\eta $
determines algebraic closures
$\eta $
determines algebraic closures
 $\bar k$
,
$\bar k$
,
 $\overline L$
, of k, and
$\overline L$
, of k, and
 $L\overset {\text {def}} = \operatorname {Fr}(A)$
, respectively. We have an exact sequence of fundamental groups where
$L\overset {\text {def}} = \operatorname {Fr}(A)$
, respectively. We have an exact sequence of fundamental groups where
 $\pi _1(X,\eta )$
is the étale fundamental group of X with geometric point
$\pi _1(X,\eta )$
is the étale fundamental group of X with geometric point
 $\eta $
(cf. [Reference Saïdi21, 2.1] for more details on the definition of
$\eta $
(cf. [Reference Saïdi21, 2.1] for more details on the definition of
 $\pi _1(X,\eta )$
in case X is an affinoid),
$\pi _1(X,\eta )$
in case X is an affinoid),
 $\pi _1(X,\eta )^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Ker}[\pi _1(X,\eta )\twoheadrightarrow G_k]$
, and
$\pi _1(X,\eta )^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Ker}[\pi _1(X,\eta )\twoheadrightarrow G_k]$
, and
 $G_k\overset {\text {def}} = \operatorname {Gal} (\bar k/k)$
is the absolute Galois group of k.
$G_k\overset {\text {def}} = \operatorname {Gal} (\bar k/k)$
is the absolute Galois group of k.
In what follows, Y is a k-compactification of X.
-
• We have a commutative diagram of exact sequences of arithmetic fundamental groups
(0.2)where
 $\pi _1(Y,\eta )$
(resp.
$\pi _1(Y,\eta )$
(resp.
 $\pi _1(Y_{\bar k},\bar \eta )$
) is the étale fundamental group of Y (resp.
$\pi _1(Y_{\bar k},\bar \eta )$
) is the étale fundamental group of Y (resp.
 $Y_{\bar k}\overset {\text {def}} = Y\times _{\operatorname {Spec} k}{\operatorname {Spec} \bar k}$
) with geometric point
$Y_{\bar k}\overset {\text {def}} = Y\times _{\operatorname {Spec} k}{\operatorname {Spec} \bar k}$
) with geometric point
 $\eta $
(resp.
$\eta $
(resp.
 $\bar \eta $
which is induced by
$\bar \eta $
which is induced by
 $\eta $
). In case X is an affinoid (resp. a formal p-adic germ), the middle vertical map is induced by the rigid analytic morphism
$\eta $
). In case X is an affinoid (resp. a formal p-adic germ), the middle vertical map is induced by the rigid analytic morphism
 $X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor (resp. the scheme morphism
$X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor (resp. the scheme morphism
 $X\to Y$
).
$X\to Y$
).
-
• We write
 $X^{\operatorname {cl}}$
(resp.
$X^{\operatorname {cl}}$
(resp.
 $Y^{\operatorname {cl}}$
) for the set of closed points of X (resp. Y). For a closed point x of X (resp. Y), we write
$Y^{\operatorname {cl}}$
) for the set of closed points of X (resp. Y). For a closed point x of X (resp. Y), we write
 $k(x)$
for the residue field at x. Thus,
$k(x)$
for the residue field at x. Thus,
 $k(x)$
is a finite extension of k.
$k(x)$
is a finite extension of k. -
• We say that
 $x\in Y^{\operatorname {cl}}$
is not in X if x is not in the image of the scheme morphism
$x\in Y^{\operatorname {cl}}$
is not in X if x is not in the image of the scheme morphism
 $X\to Y$
if X is a formal p-adic germ or
$X\to Y$
if X is a formal p-adic germ or
 $x\notin X^{\operatorname {cl}}$
in case X is affinoid. In case
$x\notin X^{\operatorname {cl}}$
in case X is affinoid. In case
 $X=\operatorname {Spec} ({\mathcal {O}}_{{\mathcal {Y}},y}\otimes _{{\mathcal {O}}_k}k)$
is a formal p-adic germ, the set of closed points of Y not in X is in one-to-one correspondence with the set of closed points of Y which do not specialize in y (cf. [Reference Liu16, §10, Proposition 1.40(a)]).
$X=\operatorname {Spec} ({\mathcal {O}}_{{\mathcal {Y}},y}\otimes _{{\mathcal {O}}_k}k)$
is a formal p-adic germ, the set of closed points of Y not in X is in one-to-one correspondence with the set of closed points of Y which do not specialize in y (cf. [Reference Liu16, §10, Proposition 1.40(a)]).
Throughout §§1–3, X will denote either an affinoid p-adic curve or a formal p-adic germ. In §3, we will assume X admits a k-compactification Y which is hyperbolic and fix a choice of such a compactification throughout.
1 Geometrically abelian arithmetic fundamental groups
In this section, we investigate the structure of various geometrically abelian arithmetic fundamental groups and absolute Galois group associated with X. Let
be the geometrically abelian fundamental group of X (here,
![]() $\pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}$
denotes the maximal abelian quotient of
$\pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}$
denotes the maximal abelian quotient of
![]() $\pi _1(X,\eta )^{\operatorname {geo}}$
).
$\pi _1(X,\eta )^{\operatorname {geo}}$
).
Proposition 1.1. We use the above notations. The followings hold.
-
(i) Assume X is an affinoid. For each prime number
 $\ell $
, the pro-
$\ell $
, the pro-
 $\ell $
-Sylow subgroup of
$\ell $
-Sylow subgroup of
 $\pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}$
is pro-
$\pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}$
is pro-
 $\ell $
abelian free, of infinite rank if
$\ell $
abelian free, of infinite rank if
 $\ell =p$
, and finite (computable) rank otherwise (see [Reference Saïdi21, Theorem A] for the precise value of this rank in case
$\ell =p$
, and finite (computable) rank otherwise (see [Reference Saïdi21, Theorem A] for the precise value of this rank in case
 $\ell \neq p$
).
$\ell \neq p$
). -
(ii) Assume X is a formal p-adic germ. For each prime number
 $\ell \neq p$
, the pro-
$\ell \neq p$
, the pro-
 $\ell $
-Sylow subgroup of
$\ell $
-Sylow subgroup of
 $\pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}$
is pro-
$\pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}$
is pro-
 $\ell $
abelian free of finite computable rank (see [Reference Saïdi23, Theorem A] for the precise value of this rank).
$\ell $
abelian free of finite computable rank (see [Reference Saïdi23, Theorem A] for the precise value of this rank).
Proof. Assertion (i) follows from [Reference Saïdi21, Theorem A]. (Note that the assumption in [Reference Saïdi21, Theorem A] that X is the complement in a proper rigid analytic k-curve of the disjoint union of finitely many k-rational open disks is satisfied after a finite extension of k [cf. [Reference Fresnel and Matignon6, 2.6, Théorème 6 and Corollaire 1]].) Assertion (ii) follows from [Reference Saïdi23, Theorem A].
Let
![]() $S\overset {\text {def}} = \{x_1,\ldots ,x_n\}\subset X^{\operatorname {cl}}$
be a finite set of closed points and write
$S\overset {\text {def}} = \{x_1,\ldots ,x_n\}\subset X^{\operatorname {cl}}$
be a finite set of closed points and write
![]() $U\overset {\text {def}} = X\setminus S$
viewed as an open subscheme of X (resp.
$U\overset {\text {def}} = X\setminus S$
viewed as an open subscheme of X (resp.
![]() $X=\operatorname {Spec} A$
in case X is an affinoid). Let
$X=\operatorname {Spec} A$
in case X is an affinoid). Let
![]() $\pi _1(U,\eta )$
be the étale fundamental group of U with geometric point
$\pi _1(U,\eta )$
be the étale fundamental group of U with geometric point
![]() $\eta $
(cf. [Reference Saïdi21, 2.1] for the definition of
$\eta $
(cf. [Reference Saïdi21, 2.1] for the definition of
![]() $\pi _1(U,\eta )$
in case X is affinoid) which sits in the exact sequence
$\pi _1(U,\eta )$
in case X is affinoid) which sits in the exact sequence
where
![]() $\pi _1(U,\eta )^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Ker}[\pi _1(U,\eta ) \twoheadrightarrow G_k]$
(cf. [Reference Saïdi21, 2.1] in case X is affinoid). Let
$\pi _1(U,\eta )^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Ker}[\pi _1(U,\eta ) \twoheadrightarrow G_k]$
(cf. [Reference Saïdi21, 2.1] in case X is affinoid). Let
be the geometrically abelian fundamental group of U (here,
![]() $\pi _1(U,\eta )^{\operatorname {geo},\operatorname {ab}}$
is the maximal abelian quotient of
$\pi _1(U,\eta )^{\operatorname {geo},\operatorname {ab}}$
is the maximal abelian quotient of
![]() $\pi _1(U,\eta )^{\operatorname {geo}}$
). We have an exact sequence
$\pi _1(U,\eta )^{\operatorname {geo}}$
). We have an exact sequence
where
![]() $\widetilde {\Delta }_U\overset {\text {def}} = \operatorname {Ker} [\pi _1(U,\eta )^{(\operatorname {ab})} \twoheadrightarrow \pi _1(X,\eta )^{(\operatorname {ab})}]=\operatorname {Ker} [\pi _1(U,\eta )^{\operatorname {geo},\operatorname {ab}} \twoheadrightarrow \pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}]$
and the (surjective) map
$\widetilde {\Delta }_U\overset {\text {def}} = \operatorname {Ker} [\pi _1(U,\eta )^{(\operatorname {ab})} \twoheadrightarrow \pi _1(X,\eta )^{(\operatorname {ab})}]=\operatorname {Ker} [\pi _1(U,\eta )^{\operatorname {geo},\operatorname {ab}} \twoheadrightarrow \pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}]$
and the (surjective) map
![]() $\pi _1(U,\eta )^{(\operatorname {ab})} \twoheadrightarrow \pi _1(X,\eta )^{(\operatorname {ab})}$
is induced by the natural projection
$\pi _1(U,\eta )^{(\operatorname {ab})} \twoheadrightarrow \pi _1(X,\eta )^{(\operatorname {ab})}$
is induced by the natural projection
![]() $\pi _1(U,\eta )\twoheadrightarrow \pi _1(X,\eta )$
. Note that
$\pi _1(U,\eta )\twoheadrightarrow \pi _1(X,\eta )$
. Note that
![]() $\widetilde {\Delta }_U$
has a natural structure of
$\widetilde {\Delta }_U$
has a natural structure of
![]() $G_k$
-module.
$G_k$
-module.
Proposition 1.2. We use the above notations. There exists a natural isomorphism
 $$ \begin{align*}\prod_{i=1}^n \operatorname{Ind} _{k(x_i)}^k \hat{\mathbb{Z}}(1)\overset \sim \to \widetilde{\Delta}_U\end{align*} $$
$$ \begin{align*}\prod_{i=1}^n \operatorname{Ind} _{k(x_i)}^k \hat{\mathbb{Z}}(1)\overset \sim \to \widetilde{\Delta}_U\end{align*} $$
of
![]() $G_k$
-modules where the
$G_k$
-modules where the
![]() $(1)$
is a Tate twist.
$(1)$
is a Tate twist.
Proof. We have a natural surjective homomorphism
![]() $\prod _{i=1}^n \operatorname {Ind} _{k(x_i)}^k \hat {\mathbb {Z}}(1)\twoheadrightarrow \widetilde {\Delta }_U$
of
$\prod _{i=1}^n \operatorname {Ind} _{k(x_i)}^k \hat {\mathbb {Z}}(1)\twoheadrightarrow \widetilde {\Delta }_U$
of
![]() $G_k$
-modules mapping
$G_k$
-modules mapping
![]() $\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1)$
onto the inertia subgroup [of
$\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1)$
onto the inertia subgroup [of
![]() $\pi _1(U,\eta )^{(\operatorname {ab})}$
] at
$\pi _1(U,\eta )^{(\operatorname {ab})}$
] at
![]() $x_i$
, as follows from the structure of inertia groups of Galois extensions of Henselian discrete valuation rings of residue characteristic zero. We show this map is an isomorphism. To this end, we can, without loss of generality, assume that X admits a k-compactification Y (cf. Notations). Indeed, this holds for X affinoid (cf. [Reference Saïdi21, 2.1]), and holds after possibly replacing k by a finite field extension in case X is a formal p-adic germ (cf. Proposition 5.1) which does not alter the structure of
$x_i$
, as follows from the structure of inertia groups of Galois extensions of Henselian discrete valuation rings of residue characteristic zero. We show this map is an isomorphism. To this end, we can, without loss of generality, assume that X admits a k-compactification Y (cf. Notations). Indeed, this holds for X affinoid (cf. [Reference Saïdi21, 2.1]), and holds after possibly replacing k by a finite field extension in case X is a formal p-adic germ (cf. Proposition 5.1) which does not alter the structure of
![]() $\widetilde {\Delta }_U$
. We have a commutative diagram of exact sequences
$\widetilde {\Delta }_U$
. We have a commutative diagram of exact sequences

where
![]() $\pi _1(Y,\eta )^{(\operatorname {ab})}\overset {\text {def}} = \pi _1(Y,\eta )/\operatorname {Ker}[\pi _1(Y_{\bar k},\bar \eta )\twoheadrightarrow \pi _1(Y_{\bar k},\bar \eta )^{\operatorname {ab}}]$
and the middle vertical map is induced by the natural homomorphism
$\pi _1(Y,\eta )^{(\operatorname {ab})}\overset {\text {def}} = \pi _1(Y,\eta )/\operatorname {Ker}[\pi _1(Y_{\bar k},\bar \eta )\twoheadrightarrow \pi _1(Y_{\bar k},\bar \eta )^{\operatorname {ab}}]$
and the middle vertical map is induced by the natural homomorphism
![]() $\pi _1(X,\eta )\to \pi _1(Y,\eta )$
(cf. Notations, diagram (0.1)).
$\pi _1(X,\eta )\to \pi _1(Y,\eta )$
(cf. Notations, diagram (0.1)).
Denote by
![]() $x_i'$
the image of
$x_i'$
the image of
![]() $x_i$
in Y,
$x_i$
in Y,
![]() $\forall 1\le i\le n$
(note that
$\forall 1\le i\le n$
(note that
![]() $k(x_i)=k(x_i')$
). Let
$k(x_i)=k(x_i')$
). Let
![]() $x_0'\in Y^{\operatorname {cl}} \setminus \{x_1',\ldots ,x_n'\}$
be a closed point which is not in the image of X (cf. Notations). Write
$x_0'\in Y^{\operatorname {cl}} \setminus \{x_1',\ldots ,x_n'\}$
be a closed point which is not in the image of X (cf. Notations). Write
![]() $S'\overset {\text {def}} = \{x_0',x_1',\ldots ,x_n'\}\subset Y^{\operatorname {cl}}$
and
$S'\overset {\text {def}} = \{x_0',x_1',\ldots ,x_n'\}\subset Y^{\operatorname {cl}}$
and
![]() $V\overset {\text {def}} = Y\setminus S'$
which is an affine k-curve. Let
$V\overset {\text {def}} = Y\setminus S'$
which is an affine k-curve. Let
![]() $\pi _1(V,\eta )$
be the étale fundamental group of V with geometric point
$\pi _1(V,\eta )$
be the étale fundamental group of V with geometric point
![]() $\eta $
which sits in the exact sequence
$\eta $
which sits in the exact sequence
![]() $1\to \pi _1(V_{\bar k},\bar \eta )\to \pi _1(V,\eta )\to G_k \to 1,$
where
$1\to \pi _1(V_{\bar k},\bar \eta )\to \pi _1(V,\eta )\to G_k \to 1,$
where
![]() $\pi _1(V_{\bar k},\bar \eta )$
is the étale fundamental group of
$\pi _1(V_{\bar k},\bar \eta )$
is the étale fundamental group of
![]() $V_{\bar k}\overset {\text {def}} = V\times _{k}\bar k$
with geometric point
$V_{\bar k}\overset {\text {def}} = V\times _{k}\bar k$
with geometric point
![]() $\bar \eta $
which is induced by
$\bar \eta $
which is induced by
![]() $\eta $
. Let
$\eta $
. Let
![]() $\pi _1(V,\eta )^{(\operatorname {ab})}\overset {\text {def}} = \pi _1(V,\eta )/\operatorname {Ker} [\pi _1(V_{\bar k},\bar \eta )\twoheadrightarrow \pi _1(V_{\bar k},\bar \eta )^{\operatorname {ab}}]$
be the geometrically abelian fundamental group of V. We have a commutative diagram of exact sequences
$\pi _1(V,\eta )^{(\operatorname {ab})}\overset {\text {def}} = \pi _1(V,\eta )/\operatorname {Ker} [\pi _1(V_{\bar k},\bar \eta )\twoheadrightarrow \pi _1(V_{\bar k},\bar \eta )^{\operatorname {ab}}]$
be the geometrically abelian fundamental group of V. We have a commutative diagram of exact sequences

where
![]() $\widetilde {\Delta }_V\overset {\text {def}} = \operatorname {Ker}[\pi _1(V,\eta )^{(\operatorname {ab})}\twoheadrightarrow \pi _1(Y,\eta )^{(\operatorname {ab})}]$
. The middle vertical map in diagram (1.3) is induced by the natural homomorphism
$\widetilde {\Delta }_V\overset {\text {def}} = \operatorname {Ker}[\pi _1(V,\eta )^{(\operatorname {ab})}\twoheadrightarrow \pi _1(Y,\eta )^{(\operatorname {ab})}]$
. The middle vertical map in diagram (1.3) is induced by the natural homomorphism
![]() $\pi _1(U,\eta )\to \pi _1(V,\eta )$
, which is induced by the scheme morphism
$\pi _1(U,\eta )\to \pi _1(V,\eta )$
, which is induced by the scheme morphism
![]() $X\to Y$
in case X is a formal p-adic germ, and by the rigid analytic morphism
$X\to Y$
in case X is a formal p-adic germ, and by the rigid analytic morphism
![]() $X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor in case X is affinoid (here, we use the fact that
$X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor in case X is affinoid (here, we use the fact that
![]() $x_0'$
is not in the image of X). The right vertical map in diagram (1.3) is the middle vertical map in diagram (1.2).
$x_0'$
is not in the image of X). The right vertical map in diagram (1.3) is the middle vertical map in diagram (1.2).
One has an exact sequence of
![]() $G_k$
-modules (as follows from the well-known structure of
$G_k$
-modules (as follows from the well-known structure of
![]() $\pi _1(V,\eta )^{(\operatorname {ab})}$
; see, e.g., the discussion in [Reference Saïdi24, §0])
$\pi _1(V,\eta )^{(\operatorname {ab})}$
; see, e.g., the discussion in [Reference Saïdi24, §0])
 $$ \begin{align*}0\to \hat{\mathbb{Z}}(1)\to \prod_{i=0}^n\operatorname{Ind}_{k(x_i')}^k \hat{\mathbb{Z}}(1)\to \widetilde{\Delta}_V\to 0.\end{align*} $$
$$ \begin{align*}0\to \hat{\mathbb{Z}}(1)\to \prod_{i=0}^n\operatorname{Ind}_{k(x_i')}^k \hat{\mathbb{Z}}(1)\to \widetilde{\Delta}_V\to 0.\end{align*} $$
Consider the composite homomorphism
![]() $\tau :\prod _{i=1}^n\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1)\to \widetilde {\Delta }_V$
of
$\tau :\prod _{i=1}^n\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1)\to \widetilde {\Delta }_V$
of
![]() $G_k$
-modules:
$G_k$
-modules:
 $$ \begin{align*}\prod_{i=1}^n\operatorname{Ind}_{k(x_i')}^k \hat{\mathbb{Z}}(1)\hookrightarrow \prod_{i=0}^n\operatorname{Ind}_{k(x_i')}^k \hat{\mathbb{Z}}(1)\twoheadrightarrow \widetilde{\Delta}_V,\end{align*} $$
$$ \begin{align*}\prod_{i=1}^n\operatorname{Ind}_{k(x_i')}^k \hat{\mathbb{Z}}(1)\hookrightarrow \prod_{i=0}^n\operatorname{Ind}_{k(x_i')}^k \hat{\mathbb{Z}}(1)\twoheadrightarrow \widetilde{\Delta}_V,\end{align*} $$
where the first map is the natural embedding:
![]() $(\beta _1,\ldots ,\beta _n)\mapsto (0,\beta _1,\ldots ,\beta _n)$
and the second map is as in the above exact sequence. Thus,
$(\beta _1,\ldots ,\beta _n)\mapsto (0,\beta _1,\ldots ,\beta _n)$
and the second map is as in the above exact sequence. Thus,
![]() $\tau $
is injective (cf. above exact sequence). Consider the following commutative diagram:
$\tau $
is injective (cf. above exact sequence). Consider the following commutative diagram:

where the right vertical map is the one in diagram (1.3). The left vertical and lower horizontal maps are as explained above; hence, their composite is the map
![]() $\tau $
. The upper horizontal map is the natural projection
$\tau $
. The upper horizontal map is the natural projection
![]() $\prod _{i=1}^n\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1) \twoheadrightarrow \widetilde {\Delta }_U$
mentioned at the start of the proof. This map is an isomorphism since it is onto and it is injective as
$\prod _{i=1}^n\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1) \twoheadrightarrow \widetilde {\Delta }_U$
mentioned at the start of the proof. This map is an isomorphism since it is onto and it is injective as
![]() $\tau $
is.
$\tau $
is.
Remark 1.3. With the notations in Proposition 1.2 and the proof therein, assume that
![]() $x^{\prime }_0\in Y(k)$
is a k-rational point. In this case
$x^{\prime }_0\in Y(k)$
is a k-rational point. In this case
![]() $\tau (\prod _{i=1}^n\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1) )=\widetilde {\Delta }_V$
, the map
$\tau (\prod _{i=1}^n\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1) )=\widetilde {\Delta }_V$
, the map
![]() $\widetilde {\Delta }_U\to \widetilde {\Delta }_V$
is an isomorphism, and the right square in diagram (1.3) (cf. proof of Proposition 1.2) is cartesian.
$\widetilde {\Delta }_U\to \widetilde {\Delta }_V$
is an isomorphism, and the right square in diagram (1.3) (cf. proof of Proposition 1.2) is cartesian.
Let
![]() $G_X\overset {\text {def}} = \operatorname {Gal} (\overline L/L)$
(recall
$G_X\overset {\text {def}} = \operatorname {Gal} (\overline L/L)$
(recall
![]() $L\overset {\text {def}} = \operatorname {Fr}(A)$
) which sits in the exact sequences
$L\overset {\text {def}} = \operatorname {Fr}(A)$
) which sits in the exact sequences
where
![]() $G_{X}^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Gal} (\overline L/L\bar k)$
, and
$G_{X}^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Gal} (\overline L/L\bar k)$
, and
where
![]() ${\mathcal {H}}_X\overset {\text {def}} = \operatorname {Ker} [G_X\twoheadrightarrow \pi _1(X,\eta )]$
. Let
${\mathcal {H}}_X\overset {\text {def}} = \operatorname {Ker} [G_X\twoheadrightarrow \pi _1(X,\eta )]$
. Let
which we shall refer to as the geometrically abelian Galois group of X (here,
![]() $G_{X}^{\operatorname {geo},\operatorname {ab}}$
is the maximal abelian quotient of
$G_{X}^{\operatorname {geo},\operatorname {ab}}$
is the maximal abelian quotient of
![]() $G_{X}^{\operatorname {geo}}$
). We have an exact sequence
$G_{X}^{\operatorname {geo}}$
). We have an exact sequence
where
![]() $\widetilde {\mathcal {H}}_X\overset {\text {def}} = \operatorname {Ker} [G_X^{(\operatorname {ab})}\twoheadrightarrow \pi _1(X,\eta )^{(\operatorname {ab})}]=\operatorname {Ker} [G_{X}^{\operatorname {geo},\operatorname {ab}}\twoheadrightarrow \pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}]$
. Note that
$\widetilde {\mathcal {H}}_X\overset {\text {def}} = \operatorname {Ker} [G_X^{(\operatorname {ab})}\twoheadrightarrow \pi _1(X,\eta )^{(\operatorname {ab})}]=\operatorname {Ker} [G_{X}^{\operatorname {geo},\operatorname {ab}}\twoheadrightarrow \pi _1(X,\eta )^{\operatorname {geo},\operatorname {ab}}]$
. Note that
![]() $\widetilde {\mathcal {H}}_X$
has a natural structure of
$\widetilde {\mathcal {H}}_X$
has a natural structure of
![]() $G_k$
-module.
$G_k$
-module.
Proposition 1.4. We use the above notations. There exists a natural isomorphism of
![]() $G_k$
-modules
$G_k$
-modules
 $$ \begin{align*}\prod _{x\in X^{\operatorname{cl}}} \operatorname{Ind} _{k(x)}^k \hat{\mathbb{Z}}(1)\overset \sim \to \widetilde {\mathcal{H}}_X,\end{align*} $$
$$ \begin{align*}\prod _{x\in X^{\operatorname{cl}}} \operatorname{Ind} _{k(x)}^k \hat{\mathbb{Z}}(1)\overset \sim \to \widetilde {\mathcal{H}}_X,\end{align*} $$
where the product is over all closed points
![]() $x\in X^{\operatorname {cl}}$
.
$x\in X^{\operatorname {cl}}$
.
Proof. This follows from Proposition 1.2 and the fact that
![]() $\widetilde {\mathcal {H}}_X\overset \sim \to \varprojlim _{U}\widetilde {\Delta } _U$
where
$\widetilde {\mathcal {H}}_X\overset \sim \to \varprojlim _{U}\widetilde {\Delta } _U$
where
![]() $U=X\setminus S$
; S runs over all finite subsets of
$U=X\setminus S$
; S runs over all finite subsets of
![]() $X^{\operatorname {cl}}$
, and
$X^{\operatorname {cl}}$
, and
![]() $\widetilde {\Delta }_U$
is as in the proof of Proposition 1.2. (Note that
$\widetilde {\Delta }_U$
is as in the proof of Proposition 1.2. (Note that
![]() $G_X^{(\operatorname {ab})}\overset \sim \to \varprojlim _{U} \pi _1(U,\eta )^{(\operatorname {ab})}$
where the limit runs over all U as above.)
$G_X^{(\operatorname {ab})}\overset \sim \to \varprojlim _{U} \pi _1(U,\eta )^{(\operatorname {ab})}$
where the limit runs over all U as above.)
2 Cuspidally abelian arithmetic fundamental groups
In this section, we investigate the problem of cuspidalization of sections of the projection
![]() $\pi _1(X,\eta )\twoheadrightarrow G_k$
. This problem has been investigated in the case of proper and smooth hyperbolic p-adic curves in [Reference Saïdi19], [Reference Saïdi22]. We use the notations in §0 and §1.
$\pi _1(X,\eta )\twoheadrightarrow G_k$
. This problem has been investigated in the case of proper and smooth hyperbolic p-adic curves in [Reference Saïdi19], [Reference Saïdi22]. We use the notations in §0 and §1.
Let
![]() $S\overset {\text {def}} = \{x_1,\ldots ,x_n\}\subset X^{\operatorname {cl}}$
be a finite set of closed points, and let
$S\overset {\text {def}} = \{x_1,\ldots ,x_n\}\subset X^{\operatorname {cl}}$
be a finite set of closed points, and let
![]() $U\overset {\text {def}} = X\setminus S$
(cf. §1). Consider the exact sequence
$U\overset {\text {def}} = X\setminus S$
(cf. §1). Consider the exact sequence
where
![]() $\Delta _U\overset {\text {def}} = \operatorname {Ker} [ \pi _1(U,\eta )^{\operatorname {geo}}\twoheadrightarrow \pi _1(X,\eta )^{\operatorname {geo}}]$
. The maximal abelian quotient
$\Delta _U\overset {\text {def}} = \operatorname {Ker} [ \pi _1(U,\eta )^{\operatorname {geo}}\twoheadrightarrow \pi _1(X,\eta )^{\operatorname {geo}}]$
. The maximal abelian quotient
![]() $\Delta _U^{\operatorname {ab}}$
of
$\Delta _U^{\operatorname {ab}}$
of
![]() $\Delta _U$
is a
$\Delta _U$
is a
![]() $\pi _1(X,\eta )^{\operatorname {geo}}$
-module. Let
$\pi _1(X,\eta )^{\operatorname {geo}}$
-module. Let
![]() $\Delta _U^{\operatorname {cn}}$
be the maximal quotient of
$\Delta _U^{\operatorname {cn}}$
be the maximal quotient of
![]() $\Delta _{U}^{\operatorname {ab}}$
on which
$\Delta _{U}^{\operatorname {ab}}$
on which
![]() $\pi _1(X,\eta )^{\operatorname {geo}}$
acts trivially. Define
$\pi _1(X,\eta )^{\operatorname {geo}}$
acts trivially. Define
and
We shall refer to
![]() $\pi _1(U,\eta )^{\operatorname {geo},\text c-\operatorname {ab}}$
(resp.
$\pi _1(U,\eta )^{\operatorname {geo},\text c-\operatorname {ab}}$
(resp.
![]() $\pi _1(U,\eta )^{\operatorname {geo},\text c-\operatorname {cn}}$
) as the cuspidally abelian (resp. cuspidally central) quotient of
$\pi _1(U,\eta )^{\operatorname {geo},\text c-\operatorname {cn}}$
) as the cuspidally abelian (resp. cuspidally central) quotient of
![]() $\pi _1(U,\eta )^{\operatorname {geo}}$
. Further, define
$\pi _1(U,\eta )^{\operatorname {geo}}$
. Further, define
and
We shall refer to
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
(resp.
$\pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
(resp.
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
) as the (geometrically) cuspidally abelian (resp. [geometrically] cuspidally central) quotient of
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
) as the (geometrically) cuspidally abelian (resp. [geometrically] cuspidally central) quotient of
![]() $\pi _1(U,\eta )$
. We have the following commutative diagram of exact sequences:
$\pi _1(U,\eta )$
. We have the following commutative diagram of exact sequences:

where the middle vertical maps are surjective, and the middle vertical map in the lower diagram is induced by the natural surjective map
![]() $\pi _1(U,\eta )^{\operatorname {geo},\text c-\operatorname {ab}}\twoheadrightarrow \pi _1(U,\eta )^{\operatorname {geo},\operatorname {ab}}$
. (Note that
$\pi _1(U,\eta )^{\operatorname {geo},\text c-\operatorname {ab}}\twoheadrightarrow \pi _1(U,\eta )^{\operatorname {geo},\operatorname {ab}}$
. (Note that
![]() $\pi _1(X,\eta )^{\operatorname {geo}}$
acts trivially on the quotient
$\pi _1(X,\eta )^{\operatorname {geo}}$
acts trivially on the quotient
![]() $\widetilde {\Delta }_U$
of
$\widetilde {\Delta }_U$
of
![]() $\Delta _U^{\operatorname {ab}}$
.)
$\Delta _U^{\operatorname {ab}}$
.)
Lemma 2.1. We use the above notations. The homomorphism
![]() $\Delta _U^{\operatorname {cn}}\to \widetilde {\Delta }_U$
in diagram (2.1) is an isomorphism of
$\Delta _U^{\operatorname {cn}}\to \widetilde {\Delta }_U$
in diagram (2.1) is an isomorphism of
![]() $G_k$
-modules. In particular, the lower right square in diagram (2.1) is Cartesian.
$G_k$
-modules. In particular, the lower right square in diagram (2.1) is Cartesian.
Proof. The proof follows from Proposition 1.2 and the various definitions. More precisely, there exists a natural surjective homomorphism
![]() $\prod _{i=1}^n\operatorname {Ind}_{k(x_i)}^k \hat {\mathbb {Z}}(1)\twoheadrightarrow \Delta _U^{\operatorname {cn}}$
(mapping
$\prod _{i=1}^n\operatorname {Ind}_{k(x_i)}^k \hat {\mathbb {Z}}(1)\twoheadrightarrow \Delta _U^{\operatorname {cn}}$
(mapping
![]() $\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1)$
onto the inertia subgroup of
$\operatorname {Ind}_{k(x_i')}^k \hat {\mathbb {Z}}(1)$
onto the inertia subgroup of
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
at
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
at
![]() $x_i$
, as follows from the structure of inertia groups of Galois extensions of Henselian discrete valuation rings of residue characteristic zero) which composed with the projection
$x_i$
, as follows from the structure of inertia groups of Galois extensions of Henselian discrete valuation rings of residue characteristic zero) which composed with the projection
![]() $\Delta _U^{\operatorname {cn}} \twoheadrightarrow \widetilde {\Delta }_U$
is the isomorphism
$\Delta _U^{\operatorname {cn}} \twoheadrightarrow \widetilde {\Delta }_U$
is the isomorphism
![]() $\prod _{i=1}^n \operatorname {Ind} _{k(x_i)}^k \hat {\mathbb {Z}}(1)\overset \sim \to \widetilde {\Delta }_U$
in Proposition 1.2 hence our assertion.
$\prod _{i=1}^n \operatorname {Ind} _{k(x_i)}^k \hat {\mathbb {Z}}(1)\overset \sim \to \widetilde {\Delta }_U$
in Proposition 1.2 hence our assertion.
Let
![]() $s:G_k\to \pi _1(X,\eta )$
be a section of the projection
$s:G_k\to \pi _1(X,\eta )$
be a section of the projection
![]() $\pi _1(X,\eta )\twoheadrightarrow G_k$
.
$\pi _1(X,\eta )\twoheadrightarrow G_k$
.
Proposition 2.2 (Lifting of sections to cuspidally central arithmetic fundamental groups)
We use the above notations. There exists a section
![]() $s_U^{\text c-\operatorname {cn}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
of the projection
$s_U^{\text c-\operatorname {cn}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
of the projection
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:

where the right vertical map is the natural projection
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})} \twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})} \twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
![]() $\Delta _U^{\operatorname {cn}}$
) a torsor under
$\Delta _U^{\operatorname {cn}}$
) a torsor under
![]() $H^1(G_k,\Delta _U^{\operatorname {cn}})$
.
$H^1(G_k,\Delta _U^{\operatorname {cn}})$
.
Proof. Consider the commutative diagram of exact sequences

where the right square is Cartesian. Thus, the group extension
![]() $E_U$
is the pullback of the group extension
$E_U$
is the pullback of the group extension
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
by the section s. The set of (possible) splittings of the group extension
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
by the section s. The set of (possible) splittings of the group extension
![]() $E_U$
is in one-to-one correspondence with the set of sections of the projection
$E_U$
is in one-to-one correspondence with the set of sections of the projection
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})}\twoheadrightarrow G_k$
which lift the section s. We show that the group extension
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})}\twoheadrightarrow G_k$
which lift the section s. We show that the group extension
![]() $E_U$
splits.
$E_U$
splits.
To this end, we can replace k by a finite extension over which the points
![]() $\{x_i\}_{i=1}^n$
are rational, and we can also assume
$\{x_i\}_{i=1}^n$
are rational, and we can also assume
![]() $n=1$
(see the argument at the start of the proof of Lemma 2.3.1 in [Reference Saïdi19]). Further, we can replace X by a neighborhood
$n=1$
(see the argument at the start of the proof of Lemma 2.3.1 in [Reference Saïdi19]). Further, we can replace X by a neighborhood
![]() $X'$
of the section s: that is, an étale cover
$X'$
of the section s: that is, an étale cover
![]() $X'\to X$
corresponding to an open subgroup
$X'\to X$
corresponding to an open subgroup
![]() $H=\pi _1(X',\eta )\subset \pi _1(X,\eta )$
containing the image
$H=\pi _1(X',\eta )\subset \pi _1(X,\eta )$
containing the image
![]() $s(G_k)$
of s. Indeed, if
$s(G_k)$
of s. Indeed, if
![]() $U'\overset {\text {def}} = U\times _XX'$
, there exists a commutative diagram of natural homomorphisms
$U'\overset {\text {def}} = U\times _XX'$
, there exists a commutative diagram of natural homomorphisms

where the upper horizontal map is induced by the natural map
![]() $\pi _1(U',\eta ) \to \pi _1(U,\eta )$
(note
$\pi _1(U',\eta ) \to \pi _1(U,\eta )$
(note
![]() $\Delta _{U'}=\Delta _U$
and
$\Delta _{U'}=\Delta _U$
and
![]() $\pi _1(X',\eta )^{\operatorname {geo}}$
acts trivially on
$\pi _1(X',\eta )^{\operatorname {geo}}$
acts trivially on
![]() $\Delta _U^{\operatorname {cn}}$
), and the various maps in this diagram commute with the projections onto
$\Delta _U^{\operatorname {cn}}$
), and the various maps in this diagram commute with the projections onto
![]() $G_k$
. The section s induces a section
$G_k$
. The section s induces a section
![]() $\tilde s:G_k\to \pi _1(X',\eta )$
of the projection
$\tilde s:G_k\to \pi _1(X',\eta )$
of the projection
![]() $\pi _1(X',\eta )\twoheadrightarrow G_k$
, and a lifting
$\pi _1(X',\eta )\twoheadrightarrow G_k$
, and a lifting
![]() $\tilde s_{U'}^{\text c-\operatorname {cn}}:G_k\to \pi _1(U',\eta )^{(\text c-\operatorname {cn})}$
of
$\tilde s_{U'}^{\text c-\operatorname {cn}}:G_k\to \pi _1(U',\eta )^{(\text c-\operatorname {cn})}$
of
![]() $\tilde s$
(as in the statement of Proposition 2.2) induces a lifting
$\tilde s$
(as in the statement of Proposition 2.2) induces a lifting
![]() $s_U^{\text c-\operatorname {cn}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
of s as required (cf. above diagram). Now, it follows from [Reference Saïdi21, Theorem A] in case X is an affinoid, and Proposition 5.3 in this paper (cf. §5) in case X is a formal p-adic germ, that there exists (after possibly a finite extension of k) a neighborhood
$s_U^{\text c-\operatorname {cn}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
of s as required (cf. above diagram). Now, it follows from [Reference Saïdi21, Theorem A] in case X is an affinoid, and Proposition 5.3 in this paper (cf. §5) in case X is a formal p-adic germ, that there exists (after possibly a finite extension of k) a neighborhood
![]() $X'\to X$
of s with
$X'\to X$
of s with
![]() $X'$
hyperbolic (cf. Notations). We can thus assume, without loss of generality, that X possesses a k-compactification Y with Y hyperbolic and the set
$X'$
hyperbolic (cf. Notations). We can thus assume, without loss of generality, that X possesses a k-compactification Y with Y hyperbolic and the set
![]() $S\overset {\text {def}} = \{x\}\subset X(k)$
consists of a single k-rational point, in which case
$S\overset {\text {def}} = \{x\}\subset X(k)$
consists of a single k-rational point, in which case
![]() $\Delta _U^{\operatorname {cn}}\overset \sim \to \hat {\mathbb {Z}}(1)$
as a
$\Delta _U^{\operatorname {cn}}\overset \sim \to \hat {\mathbb {Z}}(1)$
as a
![]() $\pi _1(X,\eta )$
-module (cf. Lemma 2.1 and Proposition 1.2).
$\pi _1(X,\eta )$
-module (cf. Lemma 2.1 and Proposition 1.2).
Consider the following maps (here,
![]() $X=\operatorname {Spec} A$
in case X is affinoid):
$X=\operatorname {Spec} A$
in case X is affinoid):
where the map
![]() $H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1)) \hookrightarrow H^2(X,\hat {\mathbb {Z}}(1))$
arises from the Cartan–Leray spectral sequence and is injective (cf. [Reference Serre25, Proof of Proposition 1]), and the map
$H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1)) \hookrightarrow H^2(X,\hat {\mathbb {Z}}(1))$
arises from the Cartan–Leray spectral sequence and is injective (cf. [Reference Serre25, Proof of Proposition 1]), and the map
![]() $\operatorname {Pic}(X)\rightarrow H^2(X,\hat {\mathbb {Z}}(1))$
is the cycle class map arising from the Kummer exact sequence in étale topology. Let
$\operatorname {Pic}(X)\rightarrow H^2(X,\hat {\mathbb {Z}}(1))$
is the cycle class map arising from the Kummer exact sequence in étale topology. Let
![]() $[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]\in H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1))$
be the class of the group extension
$[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]\in H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1))$
be the class of the group extension
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
. The image of
$\pi _1(U,\eta )^{(\text c-\operatorname {cn})}$
. The image of
![]() $[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
in
$[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
in
![]() $H^2(X,\hat {\mathbb {Z}}(1))$
coincides with the image of the line bundle
$H^2(X,\hat {\mathbb {Z}}(1))$
coincides with the image of the line bundle
![]() ${\mathcal {O}}(x)\in \operatorname {Pic}(X)$
via the Kummer map
${\mathcal {O}}(x)\in \operatorname {Pic}(X)$
via the Kummer map
![]() $\operatorname {Pic} (X) \rightarrow H^2(X,\hat {\mathbb {Z}}(1))$
. Indeed, this follows from the following commutative diagram:
$\operatorname {Pic} (X) \rightarrow H^2(X,\hat {\mathbb {Z}}(1))$
. Indeed, this follows from the following commutative diagram:

where the right and middle vertical maps are induced by the scheme morphism
![]() $X\to Y$
if X is a formal p-adic germ, and the rigid morphism
$X\to Y$
if X is a formal p-adic germ, and the rigid morphism
![]() $X\to Y^{\operatorname {rig}}$
and the comparison theorems between étale cohomology and rigid analytic étale cohomology in case X is affinoid (cf. [Reference Hansen11, Theorem 1.8 and Theorem 1.9]). The right horizontal maps are the cycle class maps arising from the Kummer exact sequence in étale topology, and the left lower horizontal map is an isomorphism arising from the Cartan–Leray spectral sequence (cf. [Reference Mochizuki17, Proposition 1.1]). The pullback of the class
$X\to Y^{\operatorname {rig}}$
and the comparison theorems between étale cohomology and rigid analytic étale cohomology in case X is affinoid (cf. [Reference Hansen11, Theorem 1.8 and Theorem 1.9]). The right horizontal maps are the cycle class maps arising from the Kummer exact sequence in étale topology, and the left lower horizontal map is an isomorphism arising from the Cartan–Leray spectral sequence (cf. [Reference Mochizuki17, Proposition 1.1]). The pullback of the class
![]() $[\pi _1(V,\eta )^{(\text c-\operatorname {cn})}]\in H^2(\pi _1(Y,\eta ),\hat {\mathbb {Z}}(1))$
in
$[\pi _1(V,\eta )^{(\text c-\operatorname {cn})}]\in H^2(\pi _1(Y,\eta ),\hat {\mathbb {Z}}(1))$
in
![]() $H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1))$
, where V is the complement in Y of the image of
$H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1))$
, where V is the complement in Y of the image of
![]() $S=\{x\}$
(cf. [Reference Saïdi19, 2.1.1] for the definition of
$S=\{x\}$
(cf. [Reference Saïdi19, 2.1.1] for the definition of
![]() $\pi _1(V,\eta )^{(\text c-\operatorname {cn})}$
), coincides with the class
$\pi _1(V,\eta )^{(\text c-\operatorname {cn})}$
), coincides with the class
![]() $[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
(this follows from Lemma 2.1 and the various definitions). The class
$[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
(this follows from Lemma 2.1 and the various definitions). The class
![]() $[\pi _1(V,\eta )^{(\text c-\operatorname {cn})}]\in H^2(\pi _1(Y,\eta ),\hat {\mathbb {Z}}(1))\overset \sim \to H^2(Y,\hat {\mathbb {Z}}(1))$
coincides with the image of the Chern class of the line bundle
$[\pi _1(V,\eta )^{(\text c-\operatorname {cn})}]\in H^2(\pi _1(Y,\eta ),\hat {\mathbb {Z}}(1))\overset \sim \to H^2(Y,\hat {\mathbb {Z}}(1))$
coincides with the image of the Chern class of the line bundle
![]() ${\mathcal {O}}(y)\in \operatorname {Pic}(Y)$
where
${\mathcal {O}}(y)\in \operatorname {Pic}(Y)$
where
![]() $y\in Y(k)$
is the image of x (cf. [Reference Saïdi19, Proof of Lemma 2.3.1]). Thus, the image of
$y\in Y(k)$
is the image of x (cf. [Reference Saïdi19, Proof of Lemma 2.3.1]). Thus, the image of
![]() $[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
in
$[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
in
![]() $H^2(X,\hat {\mathbb {Z}}(1))$
coincides with the image of the line bundle
$H^2(X,\hat {\mathbb {Z}}(1))$
coincides with the image of the line bundle
![]() ${\mathcal {O}}(x)\in \operatorname {Pic}(X)$
via the cycle class map
${\mathcal {O}}(x)\in \operatorname {Pic}(X)$
via the cycle class map
![]() $\operatorname {Pic} (X)\rightarrow H^2(X,\hat {\mathbb {Z}}(1))$
as claimed.
$\operatorname {Pic} (X)\rightarrow H^2(X,\hat {\mathbb {Z}}(1))$
as claimed.
The Picard group
![]() $\operatorname {Pic}(X)$
is finite (cf. Proposition 4.1 in this paper in case X is affinoid and [Reference Saïdi22, Proposition 5.4] in case X is a formal p-adic germ). In particular, the image of
$\operatorname {Pic}(X)$
is finite (cf. Proposition 4.1 in this paper in case X is affinoid and [Reference Saïdi22, Proposition 5.4] in case X is a formal p-adic germ). In particular, the image of
![]() $[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
in
$[\pi _1(U,\eta )^{(\text c-\operatorname {cn})}]$
in
![]() $H^2(X,\hat {\mathbb {Z}}(1))$
and hence the class
$H^2(X,\hat {\mathbb {Z}}(1))$
and hence the class
![]() $[\pi _1(U,\eta )^{(\text {c}-\operatorname {cn})}]$
is a torsion element of
$[\pi _1(U,\eta )^{(\text {c}-\operatorname {cn})}]$
is a torsion element of
![]() $H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1))$
. The class
$H^2(\pi _1(X,\eta ),\hat {\mathbb {Z}}(1))$
. The class
![]() $[E_U]\in H^2(G_k,\hat {\mathbb {Z}}(1))$
of the group extension
$[E_U]\in H^2(G_k,\hat {\mathbb {Z}}(1))$
of the group extension
![]() $E_U$
is the image of
$E_U$
is the image of
![]() $[\pi _1(U,\eta )^{(\text {c}-\operatorname {cn})}]$
under the retraction map
$[\pi _1(U,\eta )^{(\text {c}-\operatorname {cn})}]$
under the retraction map ![]() induced by s. Hence, the class
induced by s. Hence, the class
![]() $[E_U]$
is trivial since
$[E_U]$
is trivial since
![]() $\hat {\mathbb {Z}}$
is torsion-free, and the group extension
$\hat {\mathbb {Z}}$
is torsion-free, and the group extension
![]() $E_U$
splits.
$E_U$
splits.
Theorem 2.3 (Lifting of sections to cuspidally abelian arithmetic fundamental groups)
We use the above notations. There exists a section
![]() $s_U^{\operatorname {ab}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
of the projection
$s_U^{\operatorname {ab}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
of the projection
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:
$\pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:

where the right vertical map is the natural projection
![]() $ \pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
$ \pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
$\pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
![]() $\Delta _U^{\operatorname {ab}}$
) a torsor under
$\Delta _U^{\operatorname {ab}}$
) a torsor under
![]() $H^1(G_k,\Delta _U^{\operatorname {ab}})$
.
$H^1(G_k,\Delta _U^{\operatorname {ab}})$
.
Proof. Let
![]() $\{H\}_{i\in I}$
be a projective system of open subgroups of
$\{H\}_{i\in I}$
be a projective system of open subgroups of
![]() $\pi _1(X,\eta )$
containing
$\pi _1(X,\eta )$
containing
![]() $s(G_k)$
such that
$s(G_k)$
such that
![]() $s(G_k)=\bigcap _{i\in I}H_i$
. Thus, for
$s(G_k)=\bigcap _{i\in I}H_i$
. Thus, for
![]() $i\in I$
, the open subgroup
$i\in I$
, the open subgroup
![]() $H_i$
corresponds to an étale finite cover
$H_i$
corresponds to an étale finite cover
![]() $X_i\to X$
with
$X_i\to X$
with
![]() $X_i$
geometrically connected and
$X_i$
geometrically connected and
![]() $H_i$
is identified with
$H_i$
is identified with
![]() $\pi _1(X_i,\eta )$
which sits in the exact sequence
$\pi _1(X_i,\eta )$
which sits in the exact sequence
![]() $1\to \pi _1(X_{i},\eta )^{\operatorname {geo}}\to \pi _1(X_i,\eta )\to G_k\to 1$
(the geometric point; denote also
$1\to \pi _1(X_{i},\eta )^{\operatorname {geo}}\to \pi _1(X_i,\eta )\to G_k\to 1$
(the geometric point; denote also
![]() $\eta $
, of
$\eta $
, of
![]() $X_i$
is induced by the geometric point
$X_i$
is induced by the geometric point
![]() $\eta $
of X). Further, the section s induces a section
$\eta $
of X). Further, the section s induces a section
![]() $s_i:G_k\to \pi _1(X_i,\eta )$
of the projection
$s_i:G_k\to \pi _1(X_i,\eta )$
of the projection
![]() $\pi _1(X_i,\eta )\twoheadrightarrow G_k$
. Let
$\pi _1(X_i,\eta )\twoheadrightarrow G_k$
. Let
![]() $U_i\overset {\text {def}} = U\times _XX_i$
, and let
$U_i\overset {\text {def}} = U\times _XX_i$
, and let
![]() $\pi _1(U_i,\eta )^{(\text c-\operatorname {cn})}$
be the (geometrically) cuspidally central arithmetic fundamental group of
$\pi _1(U_i,\eta )^{(\text c-\operatorname {cn})}$
be the (geometrically) cuspidally central arithmetic fundamental group of
![]() $U_i$
which sits in the exact sequence
$U_i$
which sits in the exact sequence
![]() $1\to \Delta _{U_i}^{\operatorname {cn}}\to \pi _1(U_i,\eta )^{(\text c-\operatorname {cn})}\to \pi _1(X_i,\eta )\to 1$
.
$1\to \Delta _{U_i}^{\operatorname {cn}}\to \pi _1(U_i,\eta )^{(\text c-\operatorname {cn})}\to \pi _1(X_i,\eta )\to 1$
.
Consider the following commutative diagrams:

and for
![]() $i\in I$
$i\in I$

where the right squares are Cartesian. Thus,
![]() ${\mathcal {E}}_U$
(resp.
${\mathcal {E}}_U$
(resp.
![]() $E_{U_i}$
) is the pullback of the group extension
$E_{U_i}$
) is the pullback of the group extension
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
(resp.
$\pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
(resp.
![]() $\pi _1(U_i,\eta )^{(\text c-\operatorname {cn})}$
) by the section s (resp.
$\pi _1(U_i,\eta )^{(\text c-\operatorname {cn})}$
) by the section s (resp.
![]() $s_i$
). There is a natural isomorphism
$s_i$
). There is a natural isomorphism
![]() $\Delta _U^{\operatorname {ab}}=\varprojlim _{i\in I}\Delta _{U_i}^{\operatorname {cn}}$
as follows from the facts that
$\Delta _U^{\operatorname {ab}}=\varprojlim _{i\in I}\Delta _{U_i}^{\operatorname {cn}}$
as follows from the facts that
![]() $\Delta _U=\Delta _{U_i}$
,
$\Delta _U=\Delta _{U_i}$
,
![]() $\forall i\in I$
, and given a finite quotient
$\forall i\in I$
, and given a finite quotient
![]() $\Delta _U^{\operatorname {ab}}\twoheadrightarrow H$
, there exists
$\Delta _U^{\operatorname {ab}}\twoheadrightarrow H$
, there exists
![]() $i\in I$
such that
$i\in I$
such that
![]() $\pi _1(X_i,\eta )^{\operatorname {geo}}$
acts trivially on H. Further, there is a natural isomorphism
$\pi _1(X_i,\eta )^{\operatorname {geo}}$
acts trivially on H. Further, there is a natural isomorphism
![]() ${\mathcal {E}}_U\overset \sim \to \varprojlim _{i\in I} E_{U_i}$
(the transition maps in the projective limit being surjective). The existence of a section
${\mathcal {E}}_U\overset \sim \to \varprojlim _{i\in I} E_{U_i}$
(the transition maps in the projective limit being surjective). The existence of a section
![]() $s_U^{\text c-\operatorname {ab}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
of the projection
$s_U^{\text c-\operatorname {ab}}:G_k\to \pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
of the projection
![]() $\pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s is equivalent to the splitting of the group extension
$\pi _1(U,\eta )^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s is equivalent to the splitting of the group extension
![]() ${\mathcal {E}}_U$
, and the set of those (possible) liftings
${\mathcal {E}}_U$
, and the set of those (possible) liftings
![]() $s_U^{\text c-\operatorname {ab}}$
is in one-to-one correspondence with the set of sections of the projection
$s_U^{\text c-\operatorname {ab}}$
is in one-to-one correspondence with the set of sections of the projection
![]() ${\mathcal {E}}_U\twoheadrightarrow G_k$
. The natural projection
${\mathcal {E}}_U\twoheadrightarrow G_k$
. The natural projection
![]() $E_{U_i}\twoheadrightarrow G_k$
splits for all
$E_{U_i}\twoheadrightarrow G_k$
splits for all
![]() $i\in I$
(see the proof of Proposition 2.2). We show that the group extension
$i\in I$
(see the proof of Proposition 2.2). We show that the group extension
![]() ${\mathcal {E}}_U$
splits.
${\mathcal {E}}_U$
splits.
Let
![]() $(P_j)_{j\in J}$
be a projective system of quotients
$(P_j)_{j\in J}$
be a projective system of quotients
![]() ${\mathcal {E}}_U \twoheadrightarrow P_j$
, where
${\mathcal {E}}_U \twoheadrightarrow P_j$
, where
![]() $P_j$
sits in an exact sequence
$P_j$
sits in an exact sequence
![]() $1\to F_j\to P_j\to G_k\to 1$
with
$1\to F_j\to P_j\to G_k\to 1$
with
![]() $F_j$
finite, and
$F_j$
finite, and
![]() ${\mathcal {E}}_U=\varprojlim _{j\in J}P_j$
. (More precisely, write
${\mathcal {E}}_U=\varprojlim _{j\in J}P_j$
. (More precisely, write
![]() ${\mathcal {E}}_U$
as a projective limit of finite groups
${\mathcal {E}}_U$
as a projective limit of finite groups
![]() $\{\tilde P_j\}_{j\in J}$
where
$\{\tilde P_j\}_{j\in J}$
where
![]() $\tilde P_j$
sits in an exact sequence
$\tilde P_j$
sits in an exact sequence
![]() $1\to F_j\to \tilde P_j\to G_j\to 1$
with
$1\to F_j\to \tilde P_j\to G_j\to 1$
with
![]() $G_j$
a quotient of
$G_j$
a quotient of
![]() $G_k$
and
$G_k$
and
![]() $F_j$
a quotient of
$F_j$
a quotient of
![]() $\operatorname {Ker}({\mathcal {E}}_U\twoheadrightarrow G_k)$
. Let
$\operatorname {Ker}({\mathcal {E}}_U\twoheadrightarrow G_k)$
. Let
![]() $1\to F_j\to P_j\to G_k\to 1$
be the pullback of the group extension
$1\to F_j\to P_j\to G_k\to 1$
be the pullback of the group extension
![]() $1\to F_j\to \tilde P_j\to G_j\to 1$
by
$1\to F_j\to \tilde P_j\to G_j\to 1$
by
![]() $G_k\twoheadrightarrow G_j$
. Then
$G_k\twoheadrightarrow G_j$
. Then
![]() ${\mathcal {E}}_U=\varprojlim _{j\in J}P_j$
.) The set
${\mathcal {E}}_U=\varprojlim _{j\in J}P_j$
.) The set
![]() $\operatorname {Sect}(G_k,{\mathcal {E}}_U)$
of group-theoretic sections of the projection
$\operatorname {Sect}(G_k,{\mathcal {E}}_U)$
of group-theoretic sections of the projection
![]() ${\mathcal {E}}_U\twoheadrightarrow G_k$
is naturally identified with the projective limit
${\mathcal {E}}_U\twoheadrightarrow G_k$
is naturally identified with the projective limit
![]() $\varprojlim _{j\in J}\operatorname {Sect}(G_k,P_j)$
of the sets
$\varprojlim _{j\in J}\operatorname {Sect}(G_k,P_j)$
of the sets
![]() $\operatorname {Sect}(G_k,P_j)$
of group-theoretic sections of the projections
$\operatorname {Sect}(G_k,P_j)$
of group-theoretic sections of the projections
![]() $P_j\twoheadrightarrow G_k$
,
$P_j\twoheadrightarrow G_k$
,
![]() $j\in J$
. The set
$j\in J$
. The set
![]() $\operatorname {Sect}(G_k,P_j)$
is non-empty,
$\operatorname {Sect}(G_k,P_j)$
is non-empty,
![]() $\forall j\in J$
. Indeed,
$\forall j\in J$
. Indeed,
![]() $P_j$
(being a quotient of
$P_j$
(being a quotient of
![]() ${\mathcal {E}}_U$
) is a quotient of
${\mathcal {E}}_U$
) is a quotient of
![]() $E_{U_i}$
for some
$E_{U_i}$
for some
![]() $i\in I$
, this quotient
$i\in I$
, this quotient
![]() $E_{U_i}\twoheadrightarrow P_j$
commutes with the projections onto
$E_{U_i}\twoheadrightarrow P_j$
commutes with the projections onto
![]() $G_k$
, and we know the projection
$G_k$
, and we know the projection
![]() $E_{U_i}\twoheadrightarrow G_k$
splits, and hence the projection
$E_{U_i}\twoheadrightarrow G_k$
splits, and hence the projection
![]() $P_j\twoheadrightarrow G_k$
splits. Moreover, the set
$P_j\twoheadrightarrow G_k$
splits. Moreover, the set
![]() $\operatorname {Sect} (G_k,P_j)$
is, up to conjugation by the elements of
$\operatorname {Sect} (G_k,P_j)$
is, up to conjugation by the elements of
![]() $F_j$
, a torsor under the group
$F_j$
, a torsor under the group
![]() $H^1(G_k,F_j)$
which is finite since k is a p-adic local field (cf. [Reference Neukirch, Schmidt and Wingberg18, (7.1.8) Theorem (iii)]). Thus,
$H^1(G_k,F_j)$
which is finite since k is a p-adic local field (cf. [Reference Neukirch, Schmidt and Wingberg18, (7.1.8) Theorem (iii)]). Thus,
![]() $\operatorname {Sect} (G_k,P_j)$
is a non-empty finite set. The set
$\operatorname {Sect} (G_k,P_j)$
is a non-empty finite set. The set
![]() $\operatorname {Sect} (G_k,{\mathcal {E}}_U)$
is non-empty being the projective limit of non-empty finite sets. This finishes the proof of Theorem 2.3.
$\operatorname {Sect} (G_k,{\mathcal {E}}_U)$
is non-empty being the projective limit of non-empty finite sets. This finishes the proof of Theorem 2.3.
Next, let
(cf. exact sequence (1.4) for the definition of
![]() ${\mathcal {H}}_X$
). Thus,
${\mathcal {H}}_X$
). Thus,
![]() $G_X^{(\text c-\operatorname {ab})}=\varprojlim _U \pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
where U runs over all subschemes of X as in Theorem 2.3.
$G_X^{(\text c-\operatorname {ab})}=\varprojlim _U \pi _1(U,\eta )^{(\text c-\operatorname {ab})}$
where U runs over all subschemes of X as in Theorem 2.3.
Theorem 2.4 (Lifting of sections to cuspidally abelian Galois groups)
We use the above notations. There exists a section
![]() $s^{\text c-\operatorname {ab}}:G_k\to G_X^{(\text c-\operatorname {ab})}$
of the projection
$s^{\text c-\operatorname {ab}}:G_k\to G_X^{(\text c-\operatorname {ab})}$
of the projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s, that is, which inserts in the following commutative diagram:

where the right vertical map is the natural projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
![]() ${\mathcal {H}}_X^{\operatorname {ab}}$
) a torsor under
${\mathcal {H}}_X^{\operatorname {ab}}$
) a torsor under
![]() $H^1(G_k,{\mathcal {H}}_X^{\operatorname {ab}})$
.
$H^1(G_k,{\mathcal {H}}_X^{\operatorname {ab}})$
.
Proof. The proof follows, using the natural identification
![]() $G_X^{\text c-\operatorname {ab}}\overset \sim \to \varprojlim _{U} \pi _1(U,\eta )^{\text c-\operatorname {ab}}$
(where U runs over all subschemes of X as in Theorem 2.3), from Theorem 2.3 and a similar argument in our context to the one used in the proof of Theorem 2.3.5 in [Reference Saïdi19]. Alternatively, one can use Theorem 2.3 and a similar argument to the one used at the end of the proof of Theorem 2.3.
$G_X^{\text c-\operatorname {ab}}\overset \sim \to \varprojlim _{U} \pi _1(U,\eta )^{\text c-\operatorname {ab}}$
(where U runs over all subschemes of X as in Theorem 2.3), from Theorem 2.3 and a similar argument in our context to the one used in the proof of Theorem 2.3.5 in [Reference Saïdi19]. Alternatively, one can use Theorem 2.3 and a similar argument to the one used at the end of the proof of Theorem 2.3.
The following is one of our main results in this section.
Theorem 2.5. Assume that X admits a k-compactification Y (cf. Notations). If the projection
![]() $\pi _1(X,\eta )\twoheadrightarrow G_k$
splits, then
$\pi _1(X,\eta )\twoheadrightarrow G_k$
splits, then
![]() $\operatorname {index} (Y)=1$
.
$\operatorname {index} (Y)=1$
.
Proof. Assume that the projection
![]() $\pi _1(X,\eta )\twoheadrightarrow G_k$
splits and let
$\pi _1(X,\eta )\twoheadrightarrow G_k$
splits and let
![]() $s:G_k\to \pi _1(X,\eta )$
be a section of this projection. By Theorem 2.4, there exists a section
$s:G_k\to \pi _1(X,\eta )$
be a section of this projection. By Theorem 2.4, there exists a section
![]() $s^{\text c-\operatorname {ab}}:G_k\to G_X^{(\text c-\operatorname {ab})}$
of the projection
$s^{\text c-\operatorname {ab}}:G_k\to G_X^{(\text c-\operatorname {ab})}$
of the projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s. The section
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section s. The section
![]() $s^{\text c-\operatorname {ab}}$
induces naturally a section
$s^{\text c-\operatorname {ab}}$
induces naturally a section
![]() $\tilde s:G_k\to G_X^{(\operatorname {ab})}$
of the projection
$\tilde s:G_k\to G_X^{(\operatorname {ab})}$
of the projection
![]() $G_X^{(\operatorname {ab})}\twoheadrightarrow G_k$
(see §1 for the definition of
$G_X^{(\operatorname {ab})}\twoheadrightarrow G_k$
(see §1 for the definition of
![]() $G_X^{(\operatorname {ab})}$
and note that
$G_X^{(\operatorname {ab})}$
and note that
![]() $G_X^{(\operatorname {ab})}$
is a quotient of
$G_X^{(\operatorname {ab})}$
is a quotient of
![]() $G_X^{(\text c-\operatorname {ab})}$
). Let
$G_X^{(\text c-\operatorname {ab})}$
). Let
![]() $G_Y\overset {\text {def}} = \operatorname {Gal} (\overline K/K)$
be the absolute Galois group of the function field K of Y, and let
$G_Y\overset {\text {def}} = \operatorname {Gal} (\overline K/K)$
be the absolute Galois group of the function field K of Y, and let
![]() $G_Y^{(\operatorname {ab})}\overset {\text {def}} = G_Y/\operatorname {Ker} [ \operatorname {Gal} (\overline K/K\bar k)\twoheadrightarrow \operatorname {Gal} (\overline K/K\bar k)^{\operatorname {ab}} ]$
be its geometrically abelian quotient. We have a commutative diagram
$G_Y^{(\operatorname {ab})}\overset {\text {def}} = G_Y/\operatorname {Ker} [ \operatorname {Gal} (\overline K/K\bar k)\twoheadrightarrow \operatorname {Gal} (\overline K/K\bar k)^{\operatorname {ab}} ]$
be its geometrically abelian quotient. We have a commutative diagram

where the left vertical map is induced by the natural map
![]() $G_X\to G_Y$
, which is induced by the scheme morphism
$G_X\to G_Y$
, which is induced by the scheme morphism
![]() $X\to Y$
in case X is a formal p-adic germ, and by the rigid analytic morphism
$X\to Y$
in case X is a formal p-adic germ, and by the rigid analytic morphism
![]() $X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor in case X is affinoid. The section
$X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor in case X is affinoid. The section
![]() $\tilde s:G_k\to G_X^{(\operatorname {ab})}$
induces a section
$\tilde s:G_k\to G_X^{(\operatorname {ab})}$
induces a section
![]() $s^{\dagger }:G_k\to G_Y^{(\operatorname {ab})}$
of the projection
$s^{\dagger }:G_k\to G_Y^{(\operatorname {ab})}$
of the projection
![]() $G_Y^{(\operatorname {ab})}\twoheadrightarrow G_k$
(cf. above diagram). The existence of the section
$G_Y^{(\operatorname {ab})}\twoheadrightarrow G_k$
(cf. above diagram). The existence of the section
![]() $s^{\dagger }$
implies that
$s^{\dagger }$
implies that
![]() $\operatorname {index} (Y)=1$
as was observed by Esnault and Wittenberg (see [Reference Esnault and Wittenberg5, Remark 2.3(ii)] and [Reference Saïdi24, Theorem A] for a more general result).
$\operatorname {index} (Y)=1$
as was observed by Esnault and Wittenberg (see [Reference Esnault and Wittenberg5, Remark 2.3(ii)] and [Reference Saïdi24, Theorem A] for a more general result).
3 Geometric sections of arithmetic fundamental groups
We investigate geometric sections of the projection
![]() $\pi _1(X,\eta )\twoheadrightarrow G_k$
(relative to a fixed compactification of X). We use the notations in §§0–2. We further assume that X possesses a k-compactification Y with Y hyperbolic (cf. Notations) which is fixed throughout §3.
$\pi _1(X,\eta )\twoheadrightarrow G_k$
(relative to a fixed compactification of X). We use the notations in §§0–2. We further assume that X possesses a k-compactification Y with Y hyperbolic (cf. Notations) which is fixed throughout §3.
Let
be a section of the projection
![]() $\pi _1(X,\eta )\twoheadrightarrow G_k$
fixed throughout §3, which induces a (local) section
$\pi _1(X,\eta )\twoheadrightarrow G_k$
fixed throughout §3, which induces a (local) section
of the projection
![]() $\pi _1(Y,\eta )\twoheadrightarrow G_k$
(cf. diagram (0.1) and §0).
$\pi _1(Y,\eta )\twoheadrightarrow G_k$
(cf. diagram (0.1) and §0).
We have an exact sequence
where
![]() $G_Y=\operatorname {Gal} (\overline K/K)$
is the absolute Galois group of the function field K of Y and
$G_Y=\operatorname {Gal} (\overline K/K)$
is the absolute Galois group of the function field K of Y and
![]() ${\mathcal {I}}_Y\overset {\text {def}} = \operatorname {Ker}[G_Y\twoheadrightarrow \pi _1(Y,\eta )]$
. Let
${\mathcal {I}}_Y\overset {\text {def}} = \operatorname {Ker}[G_Y\twoheadrightarrow \pi _1(Y,\eta )]$
. Let
Thus,
![]() $G_Y^{(\text c-\operatorname {ab})}=\varprojlim _V \pi _1(V,\eta )^{(\text c-\operatorname {ab})}$
where V runs over all open subschemes of Y (cf. [Reference Saïdi19, 2.1.1] for the definition of
$G_Y^{(\text c-\operatorname {ab})}=\varprojlim _V \pi _1(V,\eta )^{(\text c-\operatorname {ab})}$
where V runs over all open subschemes of Y (cf. [Reference Saïdi19, 2.1.1] for the definition of
![]() $\pi _1(V,\eta )^{(\text c-\operatorname {ab})}$
).
$\pi _1(V,\eta )^{(\text c-\operatorname {ab})}$
).
Theorem 3.1 (Lifting of sections to cuspidally abelian Galois groups)
We use the above notations. The followings hold.
(i) There exists a section
![]() $s_Y^{\text c-\operatorname {ab}}:G_k\to G_Y^{(\text c-\operatorname {ab})}$
of the projection
$s_Y^{\text c-\operatorname {ab}}:G_k\to G_Y^{(\text c-\operatorname {ab})}$
of the projection
![]() $G_Y^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section
$G_Y^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lifts the section
![]() $s_Y:G_k\to \pi _1(Y,\eta )$
, that is, which inserts in the following commutative diagram:
$s_Y:G_k\to \pi _1(Y,\eta )$
, that is, which inserts in the following commutative diagram:

where the right vertical map is the natural projection
![]() $G_Y^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(Y,\eta )$
. In particular, the set of sections of the projection
$G_Y^{(\text c-\operatorname {ab})}\twoheadrightarrow \pi _1(Y,\eta )$
. In particular, the set of sections of the projection
![]() $G_Y^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section
$G_Y^{(\text c-\operatorname {ab})}\twoheadrightarrow G_k$
which lift the section
![]() $s_Y$
is non-empty, and is (up to conjugation by elements of
$s_Y$
is non-empty, and is (up to conjugation by elements of
![]() ${\mathcal {I}}_Y^{\operatorname {ab}}$
) a torsor under
${\mathcal {I}}_Y^{\operatorname {ab}}$
) a torsor under
![]() $H^1(G_k,{\mathcal {I}}_Y^{\operatorname {ab}})$
.
$H^1(G_k,{\mathcal {I}}_Y^{\operatorname {ab}})$
.
(ii) The (local) section
![]() $s_Y:G_k\to \pi _1(Y,\eta )$
is uniformly orthogonal to
$s_Y:G_k\to \pi _1(Y,\eta )$
is uniformly orthogonal to
![]() $\operatorname {Pic}$
in the sense of [Reference Saïdi19, Definition 1.4.1].
$\operatorname {Pic}$
in the sense of [Reference Saïdi19, Definition 1.4.1].
Proof. Assertion (i) follows from Theorem 2.4 and the fact that there exists a natural homomorphism
![]() $G_X^{(\text c-\operatorname {ab})}\to G_Y^{(\text c-\operatorname {ab})}$
, induced by the natural homomorphism
$G_X^{(\text c-\operatorname {ab})}\to G_Y^{(\text c-\operatorname {ab})}$
, induced by the natural homomorphism
![]() $G_X\to G_Y$
, which commutes with the projections to
$G_X\to G_Y$
, which commutes with the projections to
![]() $G_k$
. Assertion (ii) follows from assertion (i) and Theorem 2.3.5 in [Reference Saïdi19].
$G_k$
. Assertion (ii) follows from assertion (i) and Theorem 2.3.5 in [Reference Saïdi19].
Consider the following push-out diagram:

where
![]() ${\mathcal {H}}_{X,1/p^2}$
is the maximal
${\mathcal {H}}_{X,1/p^2}$
is the maximal
![]() $1/p^2$
-th solvable quotient of
$1/p^2$
-th solvable quotient of
![]() ${\mathcal {H}}_X$
and
${\mathcal {H}}_X$
and
![]() $G_X ^{(1/p^2-\operatorname {sol})}\overset {\text {def}} = G_X/\operatorname {Ker} ( {\mathcal {H}}_X \twoheadrightarrow {\mathcal {H}}_{X,1/p^2})$
. Thus,
$G_X ^{(1/p^2-\operatorname {sol})}\overset {\text {def}} = G_X/\operatorname {Ker} ( {\mathcal {H}}_X \twoheadrightarrow {\mathcal {H}}_{X,1/p^2})$
. Thus,
![]() ${\mathcal {H}}_{X,1/p^2}$
is the maximal quotient of
${\mathcal {H}}_{X,1/p^2}$
is the maximal quotient of
![]() ${\mathcal {H}}_X$
which is abelian and annihilated by
${\mathcal {H}}_X$
which is abelian and annihilated by
![]() $p^2$
(cf. [Reference Saïdi22, 1.2] for more details). We have a commutative diagram of exact sequences
$p^2$
(cf. [Reference Saïdi22, 1.2] for more details). We have a commutative diagram of exact sequences

which is induced by the natural homomorphism
![]() $G_X\to G_Y$
, where
$G_X\to G_Y$
, where
![]() $G_{Y}^{(1/p^2-\operatorname {sol})}$
is defined in a similar way to
$G_{Y}^{(1/p^2-\operatorname {sol})}$
is defined in a similar way to
![]() $G_{X}^{(1/p^2-\operatorname {sol})}$
. More precisely,
$G_{X}^{(1/p^2-\operatorname {sol})}$
. More precisely,
![]() ${\mathcal {I}}_{Y,1/p^2}$
is the maximal quotient of
${\mathcal {I}}_{Y,1/p^2}$
is the maximal quotient of
![]() ${\mathcal {I}}_Y$
which is abelian and annihilated by
${\mathcal {I}}_Y$
which is abelian and annihilated by
![]() $p^2$
and
$p^2$
and
![]() $G_Y ^{(1/p^2-\operatorname {sol})}\overset {\text {def}} = G_Y/\operatorname {Ker} ( {\mathcal {I}}_Y \twoheadrightarrow {\mathcal {I}}_{Y,1/p^2})$
is the geometrically cuspidally
$G_Y ^{(1/p^2-\operatorname {sol})}\overset {\text {def}} = G_Y/\operatorname {Ker} ( {\mathcal {I}}_Y \twoheadrightarrow {\mathcal {I}}_{Y,1/p^2})$
is the geometrically cuspidally
![]() $1/p^2$
-th step solvable quotient of
$1/p^2$
-th step solvable quotient of
![]() $G_Y$
(cf. [Reference Saïdi22, 3.1]; recall the exact sequence
$G_Y$
(cf. [Reference Saïdi22, 3.1]; recall the exact sequence
![]() $1 \to {\mathcal {I}}_{Y} \to G_Y \to \pi _1(Y,\eta ) \to 1$
).
$1 \to {\mathcal {I}}_{Y} \to G_Y \to \pi _1(Y,\eta ) \to 1$
).
The following Proposition 3.2, item (i), is weaker than (and follows from) Theorem 2.4, and we state it in connection with Theorem 3.5.2 in this section.
Proposition 3.2 (Lifting of sections to cuspidally
 $1/p^2$
-th step solvable Galois groups)
$1/p^2$
-th step solvable Galois groups)
We use the above notations. The followings hold.
(i) There exists a section
![]() $\tilde s:G_k\to G_X^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s:G_k\to G_X^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_X^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
which lifts the section
$G_X^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
which lifts the section
![]() $s:G_k\to \pi _1(X,\eta )$
, that is, which inserts in the following commutative diagram:
$s:G_k\to \pi _1(X,\eta )$
, that is, which inserts in the following commutative diagram:

where the right vertical map is the natural projection
![]() $G_X^{(1/p^2-\operatorname {sol})}\twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
$G_X^{(1/p^2-\operatorname {sol})}\twoheadrightarrow \pi _1(X,\eta )$
. In particular, the set of sections of the projection
![]() $G_X^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
$G_X^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
which lift the section s is non-empty, and is (up to conjugation by elements of
![]() ${\mathcal {H}}_{X,1/p^2}$
) a torsor under
${\mathcal {H}}_{X,1/p^2}$
) a torsor under
![]() $H^1(G_k,{\mathcal {H}}_{X,1/p^2})$
.
$H^1(G_k,{\mathcal {H}}_{X,1/p^2})$
.
(ii) The section
![]() $\tilde s:G_k\to G_X^{(1/p^2-\operatorname {sol})}$
in (i) induces a section
$\tilde s:G_k\to G_X^{(1/p^2-\operatorname {sol})}$
in (i) induces a section
![]() $\tilde s_Y:G_k\to G_Y^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s_Y:G_k\to G_Y^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_Y^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
which lifts the section
$G_Y^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
which lifts the section
![]() $s_Y:G_k\to \pi _1(Y,\eta )$
. In particular, the (local) section
$s_Y:G_k\to \pi _1(Y,\eta )$
. In particular, the (local) section
![]() $s_Y:G_k\to \pi _1(Y,\eta )$
is uniformly orthogonal to
$s_Y:G_k\to \pi _1(Y,\eta )$
is uniformly orthogonal to
![]() $\operatorname {Pic}$
mod-
$\operatorname {Pic}$
mod-
![]() $p^2$
in the sense of [Reference Saïdi22, Definition 3.4.1].
$p^2$
in the sense of [Reference Saïdi22, Definition 3.4.1].
Proof. Assertion (i) follows from Theorem 2.4 and the fact that there exists a natural projection
![]() $G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_X^{(1/p^2-\operatorname {sol})}$
which commutes with the projections onto
$G_X^{(\text c-\operatorname {ab})}\twoheadrightarrow G_X^{(1/p^2-\operatorname {sol})}$
which commutes with the projections onto
![]() $G_k$
. Assertion (ii) follows from (i) and the fact that there exists a natural homomorphism
$G_k$
. Assertion (ii) follows from (i) and the fact that there exists a natural homomorphism
![]() $G_X^{(1/p^2-\operatorname {sol})}\to G_Y^{(1/p^2-\operatorname {sol})}$
, induced by the homomorphism
$G_X^{(1/p^2-\operatorname {sol})}\to G_Y^{(1/p^2-\operatorname {sol})}$
, induced by the homomorphism
![]() $G_X\to G_Y$
, which commutes with the projections onto
$G_X\to G_Y$
, which commutes with the projections onto
![]() $G_k$
(cf. diagram (3.1) and [Reference Saïdi22, Theorem 3.4.4]).
$G_k$
(cf. diagram (3.1) and [Reference Saïdi22, Theorem 3.4.4]).
3.3
Write
 $$ \begin{align*}\Pi_Y[X]\overset{\text{def}}= \varprojlim _{T\subset Y\setminus X}\pi_1(Y\setminus T,\eta)\end{align*} $$
$$ \begin{align*}\Pi_Y[X]\overset{\text{def}}= \varprojlim _{T\subset Y\setminus X}\pi_1(Y\setminus T,\eta)\end{align*} $$
and
 $$ \begin{align*}\Pi_Y[X]^{\operatorname{geo}}\overset{\text{def}}= \varprojlim _{T\subset Y\setminus X}\pi_1(Y\setminus T,\eta)^{\operatorname{geo}},\end{align*} $$
$$ \begin{align*}\Pi_Y[X]^{\operatorname{geo}}\overset{\text{def}}= \varprojlim _{T\subset Y\setminus X}\pi_1(Y\setminus T,\eta)^{\operatorname{geo}},\end{align*} $$
where the limits are over all subsets T consisting of finitely many closed points of Y not in X (cf. Notations),
![]() $Y\setminus T$
is the corresponding (affine if T is non-empty) curve, and
$Y\setminus T$
is the corresponding (affine if T is non-empty) curve, and
![]() $\pi _1(Y\setminus T,\eta )^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Ker} [\pi _1(Y\setminus T,\eta )\twoheadrightarrow G_k]$
. We have the following commutative diagram of exact sequences:
$\pi _1(Y\setminus T,\eta )^{\operatorname {geo}}\overset {\text {def}} = \operatorname {Ker} [\pi _1(Y\setminus T,\eta )\twoheadrightarrow G_k]$
. We have the following commutative diagram of exact sequences:

where the middle upper map is induced by the rigid analytic morphism
![]() $X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor in case X is affinoid, and the scheme morphism
$X\to Y^{\operatorname {rig}}$
and the rigid GAGA functor in case X is affinoid, and the scheme morphism
![]() $X\to Y$
in case X is a formal p-adic germ. The left and middle lower vertical maps are the natural projections (they are surjective).
$X\to Y$
in case X is a formal p-adic germ. The left and middle lower vertical maps are the natural projections (they are surjective).
Proposition 3.3.1. We use the above notations. The left and middle upper vertical maps in diagram (3.2) are injective in the case X is affinoid.
Proof. The first assertion follows from Theorem A in [Reference Saïdi21] (see the comments in the proof of Proposition 1.1). The second assertion follows from the first and the commutativity of the upper part in diagram (3.2).
The section
![]() $s:G_k\to \pi _1(X,\eta )$
induces a section (denoted also s)
$s:G_k\to \pi _1(X,\eta )$
induces a section (denoted also s)
of the projections
![]() $\Pi _Y[X] \twoheadrightarrow G_k$
(cf. diagram (3.2)).
$\Pi _Y[X] \twoheadrightarrow G_k$
(cf. diagram (3.2)).
Definition 3.3.2. We say that the section s is geometric, relative to Y, if the image
![]() $s(G_k)$
of the section
$s(G_k)$
of the section
![]() $s:G_k\to \Pi _Y[X]$
is contained in a decomposition group
$s:G_k\to \Pi _Y[X]$
is contained in a decomposition group
![]() $D_x\subset \Pi _Y[X]$
associated with a rational point
$D_x\subset \Pi _Y[X]$
associated with a rational point
![]() $x\in Y(k)$
.
$x\in Y(k)$
.
Note that if s is geometric in the above sense, associated with
![]() $x\in Y(k)$
, then the (local) section
$x\in Y(k)$
, then the (local) section
![]() $s_Y:G_k\to \pi _1(Y,\eta )$
of the projection
$s_Y:G_k\to \pi _1(Y,\eta )$
of the projection
![]() $\pi _1(Y,\eta )\twoheadrightarrow G_k$
induced by s is geometric and is associated with
$\pi _1(Y,\eta )\twoheadrightarrow G_k$
induced by s is geometric and is associated with
![]() $x\in Y(k)$
, that is,
$x\in Y(k)$
, that is,
![]() $s_Y(G_k)$
is contained in (hence equal to) a decomposition group
$s_Y(G_k)$
is contained in (hence equal to) a decomposition group
![]() $D_x\subset \pi _1(Y,\eta )$
associated to x.
$D_x\subset \pi _1(Y,\eta )$
associated to x.
3.4
In this subsection, we assume that
![]() $X=\operatorname {Spec} (A\otimes _{{\mathcal {O}}_k}k)$
is a formal p-adic germ.
$X=\operatorname {Spec} (A\otimes _{{\mathcal {O}}_k}k)$
is a formal p-adic germ.
Let
![]() ${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_k$
be a model of Y, let
${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_k$
be a model of Y, let
![]() $y\in {\mathcal {Y}}^{\operatorname {cl}}$
be a closed point, and let
$y\in {\mathcal {Y}}^{\operatorname {cl}}$
be a closed point, and let
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
be an isomorphism. Let
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
be an isomorphism. Let
![]() ${\mathcal {Y}}_F\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} {\mathcal {O}}_k}\operatorname {Spec} F$
be the special fiber of
${\mathcal {Y}}_F\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} {\mathcal {O}}_k}\operatorname {Spec} F$
be the special fiber of
![]() ${\mathcal {Y}}$
. Consider the following assumption (*):
${\mathcal {Y}}$
. Consider the following assumption (*):
(*) The gcd of the total multiplicities of the irreducible components of
![]() ${\mathcal {Y}}_F$
is
${\mathcal {Y}}_F$
is
![]() $1$
.
$1$
.
Let
![]() $\xi $
be a geometric point of
$\xi $
be a geometric point of
![]() ${\mathcal {Y}}_F$
with values in the generic point of an irreducible component
${\mathcal {Y}}_F$
with values in the generic point of an irreducible component
![]() $Y_{i_0}$
of
$Y_{i_0}$
of
![]() ${\mathcal {Y}}_F$
. Thus,
${\mathcal {Y}}_F$
. Thus,
![]() $\xi $
determines an algebraic closure
$\xi $
determines an algebraic closure
![]() $\overline F$
of F. We have the following commutative diagram of exact sequences:
$\overline F$
of F. We have the following commutative diagram of exact sequences:

where the middle upper map is induced by the scheme morphism
![]() $X\to Y$
, the lower middle map (which is defined up to conjugation) is a specialization map,
$X\to Y$
, the lower middle map (which is defined up to conjugation) is a specialization map,
![]() $\pi _1({\mathcal {Y}}_F,\xi )$
(resp.
$\pi _1({\mathcal {Y}}_F,\xi )$
(resp.
![]() $\pi _1({\mathcal {Y}}_{\overline F},\bar \xi )$
) is the fundamental group of
$\pi _1({\mathcal {Y}}_{\overline F},\bar \xi )$
) is the fundamental group of
![]() ${\mathcal {Y}}$
(resp.
${\mathcal {Y}}$
(resp.
![]() ${\mathcal {Y}}_{\overline F}\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} {\mathcal {O}}_k}\operatorname {Spec} \overline F$
) with geometric point
${\mathcal {Y}}_{\overline F}\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} {\mathcal {O}}_k}\operatorname {Spec} \overline F$
) with geometric point
![]() $\xi $
(resp.
$\xi $
(resp.
![]() $\bar \xi $
which is induced by
$\bar \xi $
which is induced by
![]() $\xi $
),
$\xi $
),
![]() $G_F\overset {\text {def}} = \operatorname {Gal} (\overline F/F)$
, and the lower right vertical map is the natural projection
$G_F\overset {\text {def}} = \operatorname {Gal} (\overline F/F)$
, and the lower right vertical map is the natural projection
![]() $G_k\twoheadrightarrow G_F$
(cf. [Reference Saïdi20, diagram 0.1] and the discussion thereafter). The left (hence also the middle) lower vertical map in diagram (3.3) is surjective under the assumption (*) (cf. [Reference Saïdi20, diagram 0.1] and the references therein).
$G_k\twoheadrightarrow G_F$
(cf. [Reference Saïdi20, diagram 0.1] and the discussion thereafter). The left (hence also the middle) lower vertical map in diagram (3.3) is surjective under the assumption (*) (cf. [Reference Saïdi20, diagram 0.1] and the references therein).
The section
![]() $s:G_k\to \pi _1(X,\eta )$
induces the (local) section
$s:G_k\to \pi _1(X,\eta )$
induces the (local) section
![]() $s_Y:G_k\to \pi _1(Y,\eta )$
of the projection
$s_Y:G_k\to \pi _1(Y,\eta )$
of the projection
![]() $\pi _1(Y,\eta )\twoheadrightarrow G_k$
, as well as a homomorphism
$\pi _1(Y,\eta )\twoheadrightarrow G_k$
, as well as a homomorphism
obtained by composing the section
![]() $s_Y:G_k\to \pi _1(Y,\eta )$
with the specialization map
$s_Y:G_k\to \pi _1(Y,\eta )$
with the specialization map
![]() $\pi _1(Y,\eta )\twoheadrightarrow \pi _1({\mathcal {Y}}_F,\xi )$
in diagram (3.3).
$\pi _1(Y,\eta )\twoheadrightarrow \pi _1({\mathcal {Y}}_F,\xi )$
in diagram (3.3).
Lemma 3.4.1. We use the above notations. The followings hold.
-
(i) The closed point
 $y\in {\mathcal {Y}}^{\operatorname {cl}}$
is an F-rational point.
$y\in {\mathcal {Y}}^{\operatorname {cl}}$
is an F-rational point. -
(ii) The section
 $s_Y$
is unramified: the homomorphism
$s_Y$
is unramified: the homomorphism
 $\tilde s:G_k\to \pi _1({\mathcal {Y}}_F,\xi )$
factors through
$\tilde s:G_k\to \pi _1({\mathcal {Y}}_F,\xi )$
factors through
 $G_F$
and induces a section
$G_F$
and induces a section
 $\bar s_Y:G_F\to \pi _1({\mathcal {Y}}_F,\xi )$
of the natural projection
$\bar s_Y:G_F\to \pi _1({\mathcal {Y}}_F,\xi )$
of the natural projection
 $\pi _1({\mathcal {Y}}_F,\xi )\twoheadrightarrow G_F$
.
$\pi _1({\mathcal {Y}}_F,\xi )\twoheadrightarrow G_F$
. -
(iii) The section
 $\bar s_Y:G_F\to \pi _1({\mathcal {Y}}_F,\xi )$
in (ii) is geometric and arises from the rational point y, that is, arises from the scheme-theoretic morphism
$\bar s_Y:G_F\to \pi _1({\mathcal {Y}}_F,\xi )$
in (ii) is geometric and arises from the rational point y, that is, arises from the scheme-theoretic morphism
 $y:\operatorname {Spec} F\to {\mathcal {Y}}_F$
.
$y:\operatorname {Spec} F\to {\mathcal {Y}}_F$
. -
(iv) Assume that
 ${\mathcal {Y}}$
is regular. Then condition (*) holds.
${\mathcal {Y}}$
is regular. Then condition (*) holds.
Proof. Assertion (i) is clear (recall
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
); it also follows from (ii). We prove (ii).
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
); it also follows from (ii). We prove (ii).
We have a commutative diagram of scheme morphisms

where the lower horizontal morphism is induced by the closed point y of
![]() ${\mathcal {Y}}_F$
, and the lower vertical morphisms are closed immersions. This diagram gives rise to a commutative diagram of homomorphisms between fundamental groups
${\mathcal {Y}}_F$
, and the lower vertical morphisms are closed immersions. This diagram gives rise to a commutative diagram of homomorphisms between fundamental groups

where the lower horizontal map is a section of the projection
![]() $\pi _1({\mathcal {Y}}_F,\xi )\twoheadrightarrow G_F$
arising from the F-rational point
$\pi _1({\mathcal {Y}}_F,\xi )\twoheadrightarrow G_F$
arising from the F-rational point
![]() $y\in {\mathcal {Y}}_F$
, and is defined up to conjugation, the lower vertical maps are induced by the lower vertical maps in diagram (3.4) (they are defined up to conjugation) and are isomorphisms (cf. [Reference Grothendieck8, Exposé X, Théorème 2.1] for the right vertical map
$y\in {\mathcal {Y}}_F$
, and is defined up to conjugation, the lower vertical maps are induced by the lower vertical maps in diagram (3.4) (they are defined up to conjugation) and are isomorphisms (cf. [Reference Grothendieck8, Exposé X, Théorème 2.1] for the right vertical map
![]() $\sigma $
being an isomorphism). Further, the composite
$\sigma $
being an isomorphism). Further, the composite ![]() is the composite of the middle vertical maps in diagram (3.3) as follows from the definition of the specialization map
is the composite of the middle vertical maps in diagram (3.3) as follows from the definition of the specialization map
![]() $\pi _1(Y,\eta )\to \pi _1({\mathcal {Y}}_F,\xi )$
: this map is the composite of the maps
$\pi _1(Y,\eta )\to \pi _1({\mathcal {Y}}_F,\xi )$
: this map is the composite of the maps ![]() . In particular, the homomorphism
. In particular, the homomorphism
![]() $\tilde s:G_k\to \pi _1({\mathcal {Y}}_F,\xi )$
factors through
$\tilde s:G_k\to \pi _1({\mathcal {Y}}_F,\xi )$
factors through
![]() $G_F$
and induces a section
$G_F$
and induces a section
![]() $\bar s_Y:G_F\to \pi _1({\mathcal {Y}}_F,\xi )$
of the natural projection
$\bar s_Y:G_F\to \pi _1({\mathcal {Y}}_F,\xi )$
of the natural projection
![]() $\pi _1({\mathcal {Y}}_F,\xi )\twoheadrightarrow G_F$
. This shows (ii). The section
$\pi _1({\mathcal {Y}}_F,\xi )\twoheadrightarrow G_F$
. This shows (ii). The section
![]() $\bar s_Y$
coincides (up to conjugation) with the section
$\bar s_Y$
coincides (up to conjugation) with the section ![]() in diagram (3.5), hence is geometric and arises from the F-rational point y as claimed in (iii). The last assertion follows from Theorem 2.5 and the well-known fact that if
in diagram (3.5), hence is geometric and arises from the F-rational point y as claimed in (iii). The last assertion follows from Theorem 2.5 and the well-known fact that if
![]() ${\mathcal {Y}}$
is regular, then the gcd of the total multiplicities of the irreducible components of
${\mathcal {Y}}$
is regular, then the gcd of the total multiplicities of the irreducible components of
![]() ${\mathcal {Y}}_F$
divides
${\mathcal {Y}}_F$
divides
![]() $\operatorname {index} (Y)$
(cf., e.g., [Reference Gabber, Liu and Lorenzini7, Theorem 8.2 and Remark 8.6]).
$\operatorname {index} (Y)$
(cf., e.g., [Reference Gabber, Liu and Lorenzini7, Theorem 8.2 and Remark 8.6]).
Remark 3.4.2. Assume that the morphism
![]() ${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_k$
is smooth. If s is geometric, and arises from the rational point
${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_k$
is smooth. If s is geometric, and arises from the rational point
![]() $x\in Y(k)$
(cf. Definition 3.3.2), it follows from Lemma 3.4.1(iii) and the fact that
$x\in Y(k)$
(cf. Definition 3.3.2), it follows from Lemma 3.4.1(iii) and the fact that
![]() ${\mathcal {Y}}_F$
is hyperbolic that the point x specializes in y necessarily (cf. [Reference Tamagawa27, Proposition (2.8)(i)]). In particular, the point x is the image of a (unique) k-rational point
${\mathcal {Y}}_F$
is hyperbolic that the point x specializes in y necessarily (cf. [Reference Tamagawa27, Proposition (2.8)(i)]). In particular, the point x is the image of a (unique) k-rational point
![]() $\tilde x\in X(k)$
via the morphism
$\tilde x\in X(k)$
via the morphism
![]() $X\to Y$
. The fact that
$X\to Y$
. The fact that
![]() $s_Y(G_k)=D_x\subset \pi _1(Y,\eta )$
does not imply a priori that the image
$s_Y(G_k)=D_x\subset \pi _1(Y,\eta )$
does not imply a priori that the image
![]() $s(G_k)$
via the section
$s(G_k)$
via the section
![]() $s:G_k\to \pi _1(X,\eta )$
is contained in a decomposition group
$s:G_k\to \pi _1(X,\eta )$
is contained in a decomposition group
![]() $D_{\tilde x}\subset \pi _1(X,\eta )$
associated with
$D_{\tilde x}\subset \pi _1(X,\eta )$
associated with
![]() $\tilde x$
.
$\tilde x$
.
3.5
Let
![]() $H\subset \Pi _Y[X]$
be an open subgroup with
$H\subset \Pi _Y[X]$
be an open subgroup with
![]() $s(G_k)\subset H$
[recall
$s(G_k)\subset H$
[recall
![]() $s:G_k\to \Pi _Y[X]$
is the section induced by
$s:G_k\to \Pi _Y[X]$
is the section induced by
![]() $s:G_k\to \pi _1(X,\eta )$
]. Thus, H corresponds to a (possibly ramified) finite cover
$s:G_k\to \pi _1(X,\eta )$
]. Thus, H corresponds to a (possibly ramified) finite cover
![]() $Y'\to Y$
with
$Y'\to Y$
with
![]() $Y'$
geometrically connected. Let
$Y'$
geometrically connected. Let
![]() $H' \subset \pi _1(X,\eta )$
be the inverse image of H via the homomorphism
$H' \subset \pi _1(X,\eta )$
be the inverse image of H via the homomorphism
![]() $\pi _1(X,\eta )\to \Pi _Y[X]$
(cf. diagram (3.2)). Thus,
$\pi _1(X,\eta )\to \Pi _Y[X]$
(cf. diagram (3.2)). Thus,
![]() $H'$
is an open subgroup of
$H'$
is an open subgroup of
![]() $\pi _1(X,\eta )$
containing the image of the section
$\pi _1(X,\eta )$
containing the image of the section
![]() $s:G_k\to \pi _1(X,\eta )$
and corresponds to an étale cover
$s:G_k\to \pi _1(X,\eta )$
and corresponds to an étale cover
![]() $X'\to X$
with
$X'\to X$
with
![]() $X'$
geometrically connected. There is a natural morphism
$X'$
geometrically connected. There is a natural morphism
![]() $X'\to (Y')^{\operatorname {rig}}$
of rigid analytic spaces in case X is affinoid, and a natural scheme morphism
$X'\to (Y')^{\operatorname {rig}}$
of rigid analytic spaces in case X is affinoid, and a natural scheme morphism
![]() $X'\to Y'$
in case X is a formal p-adic germ. The generic point
$X'\to Y'$
in case X is a formal p-adic germ. The generic point
![]() $\eta $
induces naturally a generic point (denoted also
$\eta $
induces naturally a generic point (denoted also
![]() $\eta $
) of
$\eta $
) of
![]() $X'$
and
$X'$
and
![]() $Y'$
. Further, we have a natural identification
$Y'$
. Further, we have a natural identification
![]() $H'=\pi _1(X',\eta )$
and a natural homomorphism
$H'=\pi _1(X',\eta )$
and a natural homomorphism
![]() $\pi _1(X',\eta )\to \pi _1(Y',\eta )$
which commutes with the projections onto
$\pi _1(X',\eta )\to \pi _1(Y',\eta )$
which commutes with the projections onto
![]() $G_k$
.
$G_k$
.
The section
![]() $s:G_k\to \pi _1(X,\eta )$
induces naturally sections
$s:G_k\to \pi _1(X,\eta )$
induces naturally sections
![]() $s':G_k\to \pi _1(X',\eta )$
and
$s':G_k\to \pi _1(X',\eta )$
and
![]() $s_{Y'}:G_k\to \pi _1(Y',\eta )$
of the natural projections
$s_{Y'}:G_k\to \pi _1(Y',\eta )$
of the natural projections
![]() $\pi _1(X',\eta )\twoheadrightarrow G_k$
and
$\pi _1(X',\eta )\twoheadrightarrow G_k$
and
![]() $\pi _1(Y',\eta )\twoheadrightarrow G_k$
, respectively. The section
$\pi _1(Y',\eta )\twoheadrightarrow G_k$
, respectively. The section
![]() $s':G_k\to \pi _1(X',\eta )$
lifts to a section
$s':G_k\to \pi _1(X',\eta )$
lifts to a section
![]() $\tilde s':G_k\to G_{X'}^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s':G_k\to G_{X'}^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_{X'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
and induces a section
$G_{X'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
and induces a section
![]() $\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
(cf. Proposition 3.2). Let
$G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
(cf. Proposition 3.2). Let
![]() $F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
be an open subgroup with
$F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
be an open subgroup with
![]() $\tilde s_{Y'}(G_k)\subset F$
. Thus, F corresponds to a (possibly ramified) finite cover
$\tilde s_{Y'}(G_k)\subset F$
. Thus, F corresponds to a (possibly ramified) finite cover
![]() $Y"\to Y'$
with
$Y"\to Y'$
with
![]() $Y"$
geometrically connected. The generic point
$Y"$
geometrically connected. The generic point
![]() $\eta $
induces naturally a generic point (denoted also
$\eta $
induces naturally a generic point (denoted also
![]() $\eta $
) of
$\eta $
) of
![]() $Y"$
. Write
$Y"$
. Write
![]() $\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}$
for the geometrically
$\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}$
for the geometrically
![]() $1/p$
-th step solvable quotient of
$1/p$
-th step solvable quotient of
![]() $\pi _1(Y",\eta )$
which sits in the following exact sequence:
$\pi _1(Y",\eta )$
which sits in the following exact sequence:
where
![]() $\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )_{1/p}$
is the maximal
$\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )_{1/p}$
is the maximal
![]() $1/p$
-th step solvable quotient of
$1/p$
-th step solvable quotient of
![]() $\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )$
(cf. [Reference Saïdi22, 1.2]) and the generic point
$\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )$
(cf. [Reference Saïdi22, 1.2]) and the generic point
![]() $\bar \eta $
is induced by
$\bar \eta $
is induced by
![]() $\eta $
. Thus,
$\eta $
. Thus,
![]() $\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )_{1/p}$
is the maximal quotient of
$\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )_{1/p}$
is the maximal quotient of
![]() $\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )$
which is abelian and annihilated by p (cf. [Reference Saïdi22, 1.2]).
$\pi _1(Y^{\prime \prime }_{\bar k},\bar \eta )$
which is abelian and annihilated by p (cf. [Reference Saïdi22, 1.2]).
Definition 3.5.1. We use the above notations. We say that the section s is admissible, relative to Y, if for every open subgroup
![]() $H\subset \Pi _Y[X]$
with
$H\subset \Pi _Y[X]$
with
![]() $s(G_k)\subset H$
, corresponding to (a possibly ramified) cover
$s(G_k)\subset H$
, corresponding to (a possibly ramified) cover
![]() $Y'\to Y$
, the following holds. There exists a section
$Y'\to Y$
, the following holds. There exists a section
![]() $\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
(such a section exists unconditionally [see above discussion]) satisfying the following property: for each open subgroup
$G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
(such a section exists unconditionally [see above discussion]) satisfying the following property: for each open subgroup
![]() $F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
with
$F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
with
![]() $\tilde s_{Y'}(G_k)\subset F$
, corresponding to a (possibly ramified) cover
$\tilde s_{Y'}(G_k)\subset F$
, corresponding to a (possibly ramified) cover
![]() $Y"\to Y'$
with
$Y"\to Y'$
with
![]() $Y"$
geometrically connected, the natural projection
$Y"$
geometrically connected, the natural projection
![]() $\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}\twoheadrightarrow G_k$
splits (cf. above discussion). Note that this latter condition is equivalent to (cf. [Reference Saïdi22, Lemma 3.4.8]): the class of
$\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}\twoheadrightarrow G_k$
splits (cf. above discussion). Note that this latter condition is equivalent to (cf. [Reference Saïdi22, Lemma 3.4.8]): the class of
![]() $\operatorname {Pic}^1_{Y"}$
in
$\operatorname {Pic}^1_{Y"}$
in
![]() $H^1(G_k,\operatorname {Pic}^0_{Y"})$
is divisible by p.
$H^1(G_k,\operatorname {Pic}^0_{Y"})$
is divisible by p.
Our main result in this section is the following.
Theorem 3.5.2. We use the above notations. The section
![]() $s:G_k\to \pi _1(X,\eta )$
is geometric relative to Y (cf. Definition 3.3.2) if and only if s is admissible relative to Y (cf. Definition 3.5.1).
$s:G_k\to \pi _1(X,\eta )$
is geometric relative to Y (cf. Definition 3.3.2) if and only if s is admissible relative to Y (cf. Definition 3.5.1).
Proof. Assume first that the section
![]() $s:G_k\to \pi _1(X,\eta )$
is admissible (relative to Y). We prove that s is geometric (relative to Y). Using a well-known limit argument due to Tamagawa (cf. [Reference Tamagawa27, Proposition 2.8(iv)]), it suffices to show the following. For every open subgroup
$s:G_k\to \pi _1(X,\eta )$
is admissible (relative to Y). We prove that s is geometric (relative to Y). Using a well-known limit argument due to Tamagawa (cf. [Reference Tamagawa27, Proposition 2.8(iv)]), it suffices to show the following. For every open subgroup
![]() $H\subset \Pi _Y[X]$
with
$H\subset \Pi _Y[X]$
with
![]() $s(G_k)\subset H$
, corresponding to (a possibly ramified) cover
$s(G_k)\subset H$
, corresponding to (a possibly ramified) cover
![]() $Y'\to Y$
with
$Y'\to Y$
with
![]() $Y'$
hyperbolic,
$Y'$
hyperbolic,
![]() $Y'(k)\neq \emptyset $
holds. By assumption, there exists a section
$Y'(k)\neq \emptyset $
holds. By assumption, there exists a section
![]() $\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
satisfying the condition in Definition 3.5.1. In [Reference Saïdi22, 3.3], we defined a certain quotient
$G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
satisfying the condition in Definition 3.5.1. In [Reference Saïdi22, 3.3], we defined a certain quotient
![]() $G_{Y'}\twoheadrightarrow G_{Y'}^{(p,2)}\twoheadrightarrow G_{Y'}^{(1/p^2-\operatorname {sol})}$
of
$G_{Y'}\twoheadrightarrow G_{Y'}^{(p,2)}\twoheadrightarrow G_{Y'}^{(1/p^2-\operatorname {sol})}$
of
![]() $G_{Y'}$
(we refer to [Reference Saïdi22, 3.3] for more details on the definition of
$G_{Y'}$
(we refer to [Reference Saïdi22, 3.3] for more details on the definition of
![]() $G_{Y'}^{(p,2)}$
). Let
$G_{Y'}^{(p,2)}$
). Let
![]() $F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
be an open subgroup with
$F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
be an open subgroup with
![]() $\tilde s_{Y'}(G_k)\subset F$
corresponding to a (possibly ramified) cover
$\tilde s_{Y'}(G_k)\subset F$
corresponding to a (possibly ramified) cover
![]() $Y"\to Y'$
with
$Y"\to Y'$
with
![]() $Y"$
geometrically connected. By assumption, the natural projection
$Y"$
geometrically connected. By assumption, the natural projection
![]() $\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}\twoheadrightarrow G_k$
splits (cf. Definition 3.5.1). This latter condition (for every F as above) implies that (in fact is equivalent to) the section
$\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}\twoheadrightarrow G_k$
splits (cf. Definition 3.5.1). This latter condition (for every F as above) implies that (in fact is equivalent to) the section
![]() $\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
lifts to a section
$\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
lifts to a section
![]() $s_{Y'}^{\dagger }:G_k\to G_{Y'}^{(p,2)}$
of the projection
$s_{Y'}^{\dagger }:G_k\to G_{Y'}^{(p,2)}$
of the projection
![]() $G_{Y'}^{(p,2)}\twoheadrightarrow G_k$
(cf. [Reference Saïdi22, Theorem 3.4.10 and Lemma 3.4.8]). Further, the existence of the section
$G_{Y'}^{(p,2)}\twoheadrightarrow G_k$
(cf. [Reference Saïdi22, Theorem 3.4.10 and Lemma 3.4.8]). Further, the existence of the section
![]() $s_{Y'}^{\dagger }:G_k\to G_{Y'}^{(p,2)}$
as above implies that
$s_{Y'}^{\dagger }:G_k\to G_{Y'}^{(p,2)}$
as above implies that
![]() $Y'(k)\neq \emptyset $
by [Reference Saïdi22, Proposition 4.6], as required.
$Y'(k)\neq \emptyset $
by [Reference Saïdi22, Proposition 4.6], as required.
Next, we assume that s is geometric (relative to Y) and prove that s is admissible (relative to Y). By assumption
![]() $s(G_k)$
is contained in
$s(G_k)$
is contained in
![]() $D_x\subset \Pi _Y[X]$
where
$D_x\subset \Pi _Y[X]$
where
![]() $D_x$
is a decomposition group associated with a rational point
$D_x$
is a decomposition group associated with a rational point
![]() $x\in Y(k)$
. Let
$x\in Y(k)$
. Let
![]() $H\subset \Pi _Y[X]$
be an open subgroup with
$H\subset \Pi _Y[X]$
be an open subgroup with
![]() $s(G_k)\subset H$
corresponding to (a possibly ramified) cover
$s(G_k)\subset H$
corresponding to (a possibly ramified) cover
![]() $Y'\to Y$
. Then
$Y'\to Y$
. Then
![]() $Y'(k)\neq \emptyset $
. A rational point
$Y'(k)\neq \emptyset $
. A rational point
![]() $x'\in Y'(k)$
gives rise to a section
$x'\in Y'(k)$
gives rise to a section
![]() $\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
$\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
of the projection
![]() $G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
. Let
$G_{Y'}^{(1/p^2-\operatorname {sol})}\twoheadrightarrow G_k$
. Let
![]() $F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
be an open subgroup with
$F\subset G_{Y'}^{(1/p^2-\operatorname {sol})}$
be an open subgroup with
![]() $\tilde s_{Y'}(G_k)\subset F$
corresponding to a (possibly ramified) cover
$\tilde s_{Y'}(G_k)\subset F$
corresponding to a (possibly ramified) cover
![]() $Y"\to Y'$
with
$Y"\to Y'$
with
![]() $Y"$
geometrically connected. Then
$Y"$
geometrically connected. Then
![]() $Y"(k)\neq \emptyset $
holds since the section
$Y"(k)\neq \emptyset $
holds since the section
![]() $\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
arises from the rational point
$\tilde s_{Y'}:G_k\to G_{Y'}^{(1/p^2-\operatorname {sol})}$
arises from the rational point
![]() $x'$
and
$x'$
and
![]() $\tilde s_{Y'}(G_k)\subset F$
. In particular, the natural projection
$\tilde s_{Y'}(G_k)\subset F$
. In particular, the natural projection
![]() $\pi _1(Y",\eta )\twoheadrightarrow G_k$
, and a fortiori the projection
$\pi _1(Y",\eta )\twoheadrightarrow G_k$
, and a fortiori the projection
![]() $\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}\twoheadrightarrow G_k$
, splits. Thus, s is admissible as required.
$\pi _1(Y",\eta )^{(1/p-\operatorname {sol})}\twoheadrightarrow G_k$
, splits. Thus, s is admissible as required.
4 Picard groups of affinoid p-adic curves
The following is our main result in this section; it may be of interest independently of the topics discussed in §§1–3.
Proposition 4.1. Let
![]() $X=\operatorname {Sp}(A)$
be a smooth and geometrically connected k-affinoid curve. Then the Picard group
$X=\operatorname {Sp}(A)$
be a smooth and geometrically connected k-affinoid curve. Then the Picard group
![]() $\operatorname {Pic}(X)$
is finite.
$\operatorname {Pic}(X)$
is finite.
The rest of this section is devoted to the proof of Proposition 4.1.
Let
![]() ${\mathcal {X}}=\operatorname {Spf} B$
be an excellent normal
${\mathcal {X}}=\operatorname {Spf} B$
be an excellent normal
![]() ${\mathcal {O}}_k$
-formal scheme of finite type with generic fiber X, that is,
${\mathcal {O}}_k$
-formal scheme of finite type with generic fiber X, that is,
![]() $A=B\otimes _R k$
. Write
$A=B\otimes _R k$
. Write
![]() ${\mathcal {X}}^{\operatorname {reg}}$
for the set of regular points of
${\mathcal {X}}^{\operatorname {reg}}$
for the set of regular points of
![]() ${\mathcal {X}}$
. Thus,
${\mathcal {X}}$
. Thus,
![]() ${\mathcal {X}}\setminus {\mathcal {X}}^{\operatorname {reg}}=\{z_1,\ldots ,z_t\}$
consists of finitely many closed points of
${\mathcal {X}}\setminus {\mathcal {X}}^{\operatorname {reg}}=\{z_1,\ldots ,z_t\}$
consists of finitely many closed points of
![]() ${\mathcal {X}}$
. By Lipman’s theorem of resolution of singularities for excellent two-dimensional schemes, there exists a birational and proper morphism
${\mathcal {X}}$
. By Lipman’s theorem of resolution of singularities for excellent two-dimensional schemes, there exists a birational and proper morphism
![]() $\lambda :{\mathcal {S}}\to {\mathcal {X}}$
with
$\lambda :{\mathcal {S}}\to {\mathcal {X}}$
with
![]() ${\mathcal {S}}$
regular and
${\mathcal {S}}$
regular and
![]() $\lambda ^{-1}({\mathcal {X}}^{\operatorname {reg}})\to {\mathcal {X}}^{\operatorname {reg}}$
an isomorphism (cf. [Reference Lipman15]; here, we view
$\lambda ^{-1}({\mathcal {X}}^{\operatorname {reg}})\to {\mathcal {X}}^{\operatorname {reg}}$
an isomorphism (cf. [Reference Lipman15]; here, we view
![]() ${\mathcal {X}}$
as the ordinary affine scheme
${\mathcal {X}}$
as the ordinary affine scheme
![]() $\operatorname {Spec} B$
). For
$\operatorname {Spec} B$
). For
![]() $n\ge 1$
, write
$n\ge 1$
, write
![]() $B_n\overset {\text {def}} = B/(\pi ^n)$
,
$B_n\overset {\text {def}} = B/(\pi ^n)$
,
![]() ${\mathcal {X}}_n\overset {\text {def}} = \operatorname {Spec} B_n$
, and
${\mathcal {X}}_n\overset {\text {def}} = \operatorname {Spec} B_n$
, and
![]() ${\mathcal {S}}_n\overset {\text {def}} = {\mathcal {S}}\times _{{\mathcal {X}}}{\mathcal {X}}_n$
. Further, denote
${\mathcal {S}}_n\overset {\text {def}} = {\mathcal {S}}\times _{{\mathcal {X}}}{\mathcal {X}}_n$
. Further, denote
![]() ${\mathcal {X}}_0\overset {\text {def}} = {\mathcal {X}}_n^{\operatorname {red}}$
and
${\mathcal {X}}_0\overset {\text {def}} = {\mathcal {X}}_n^{\operatorname {red}}$
and
![]() ${\mathcal {S}}_0\overset {\text {def}} = {\mathcal {S}}_n^{\operatorname {red}}$
. Thus,
${\mathcal {S}}_0\overset {\text {def}} = {\mathcal {S}}_n^{\operatorname {red}}$
. Thus,
![]() ${\mathcal {X}}_0$
and
${\mathcal {X}}_0$
and
![]() ${\mathcal {S}}_0$
are one-dimensional reduced schemes over F. Further, there exists a morphism
${\mathcal {S}}_0$
are one-dimensional reduced schemes over F. Further, there exists a morphism
![]() $\lambda :{\mathcal {S}}\to {\mathcal {X}}$
as above with
$\lambda :{\mathcal {S}}\to {\mathcal {X}}$
as above with
![]() $S_0$
a divisor with strict normal crossings (cf. [Reference Cossart, Jannsen and Saito3, Corollary 0.4]), which we assume from now on.
$S_0$
a divisor with strict normal crossings (cf. [Reference Cossart, Jannsen and Saito3, Corollary 0.4]), which we assume from now on.
We have a surjective homomorphism
![]() $\operatorname {Pic}({\mathcal {X}}^{\operatorname {reg}})\twoheadrightarrow \operatorname {Pic}(X)$
. To prove
$\operatorname {Pic}({\mathcal {X}}^{\operatorname {reg}})\twoheadrightarrow \operatorname {Pic}(X)$
. To prove
![]() $\operatorname {Pic}(X)$
is finite, it suffices to prove that
$\operatorname {Pic}(X)$
is finite, it suffices to prove that
![]() $\operatorname {Pic}({\mathcal {X}}^{\operatorname {reg}})$
is finite. For each singular point
$\operatorname {Pic}({\mathcal {X}}^{\operatorname {reg}})$
is finite. For each singular point
![]() $z_i$
of
$z_i$
of
![]() ${\mathcal {X}}$
, let
${\mathcal {X}}$
, let
![]() $E_i\overset {\text {def}} = \lambda ^{-1}(z_i)^{\operatorname {red}}$
and let
$E_i\overset {\text {def}} = \lambda ^{-1}(z_i)^{\operatorname {red}}$
and let
![]() $\{D_{i,j}\}_{1\le j\le n_i}$
be the set of irreducible components of
$\{D_{i,j}\}_{1\le j\le n_i}$
be the set of irreducible components of
![]() $E_i$
,
$E_i$
,
![]() $1\le i\le t$
. Thus,
$1\le i\le t$
. Thus,
![]() $E_i$
is a reduced proper curve over the residue field
$E_i$
is a reduced proper curve over the residue field
![]() $k(z_i)$
at
$k(z_i)$
at
![]() $z_i$
which is a finite field. We have an exact sequence
$z_i$
which is a finite field. We have an exact sequence
where
![]() $\beta $
maps the copy of
$\beta $
maps the copy of
![]() $\mathbb {Z}$
indexed by the pair
$\mathbb {Z}$
indexed by the pair
![]() $(i,j)$
to the class of the divisor
$(i,j)$
to the class of the divisor
![]() $D_{i,j}$
. Further, we have an isomorphism
$D_{i,j}$
. Further, we have an isomorphism
(cf. [Reference Grothendieck and Dieudonné9, première partie, Corollaire 5.1.6]).
Lemma 4.2. We use notations as above. To prove that
![]() $\operatorname {Pic}({\mathcal {X}}^{\operatorname {reg}})$
is finite, it suffices to prove the following two assertions:
$\operatorname {Pic}({\mathcal {X}}^{\operatorname {reg}})$
is finite, it suffices to prove the following two assertions:
(A) The cokernel of the composite map
is finite for
![]() $n\ge 1$
.
$n\ge 1$
.
(B) There exists
![]() $n_0>0$
such that the map
$n_0>0$
such that the map
is an isomorphism for
![]() $n>n_0$
.
$n>n_0$
.
Proof of Lemma 4.2
Follows from the above discussion and the fact that we have an exact sequence
where the first map is induced by the maps
![]() $\phi _n:M\to \operatorname {Pic} ({\mathcal {S}}_n)$
,
$\phi _n:M\to \operatorname {Pic} ({\mathcal {S}}_n)$
,
![]() $n\ge 1$
, and
$n\ge 1$
, and
![]() $\varprojlim _{n\ge 1} \text {coker}(\phi _n)$
is finite if assertions (A) and (B) are satisfied.
$\varprojlim _{n\ge 1} \text {coker}(\phi _n)$
is finite if assertions (A) and (B) are satisfied.
This finishes the proof of Lemma 4.2.
The rest of this section is devoted to the proofs of assertions (A) and (B).
Proof of assertion (A)
Let
![]() $\{\eta _r\}_{r=1}^s$
be the generic points of
$\{\eta _r\}_{r=1}^s$
be the generic points of
![]() ${\mathcal {X}}_0$
, let
${\mathcal {X}}_0$
, let
![]() $\rho :{\mathcal {S}}_0^{\text {nor}}\to {\mathcal {S}}_0$
be the morphism of normalization, let
$\rho :{\mathcal {S}}_0^{\text {nor}}\to {\mathcal {S}}_0$
be the morphism of normalization, let
![]() $\widetilde E_i\overset {\text {def}} = \rho ^{-1}(E_i)$
,
$\widetilde E_i\overset {\text {def}} = \rho ^{-1}(E_i)$
,
![]() $1\le i\le t$
, and let
$1\le i\le t$
, and let
![]() $H_r=\overline {\{\eta _r\}}$
be the closure in
$H_r=\overline {\{\eta _r\}}$
be the closure in
![]() ${\mathcal {S}}_0^{\text {nor}}$
of the (inverse image in
${\mathcal {S}}_0^{\text {nor}}$
of the (inverse image in
![]() ${\mathcal {S}}_0$
of the) generic point
${\mathcal {S}}_0$
of the) generic point
![]() $\eta _r$
of
$\eta _r$
of
![]() ${\mathcal {X}}_0$
,
${\mathcal {X}}_0$
,
![]() $1\le r\le s$
. Thus,
$1\le r\le s$
. Thus,
![]() $H_r$
is a connected affine normal one-dimensional scheme over F. Let
$H_r$
is a connected affine normal one-dimensional scheme over F. Let
be the composite map where the first map is the pullback of line bundles via the normalization morphism
![]() $\rho :{\mathcal {S}}_0^{\text {nor}}\to {\mathcal {S}}_0$
, and the map
$\rho :{\mathcal {S}}_0^{\text {nor}}\to {\mathcal {S}}_0$
, and the map
![]() $\text {deg}$
is obtained by taking the degree of a line bundle on each irreducible component
$\text {deg}$
is obtained by taking the degree of a line bundle on each irreducible component
![]() $D_{i,j}$
of
$D_{i,j}$
of
![]() $E_i$
.
$E_i$
.
Claim 1.
![]() $\text {ker}(d)$
is finite.
$\text {ker}(d)$
is finite.
Proof of Claim 1
We have a commutative diagram of exact sequences

where
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are defined so that the above sequences are exact, and
$A_2$
are defined so that the above sequences are exact, and
![]() $A_2$
is finite as follows from the facts that the sheaf
$A_2$
is finite as follows from the facts that the sheaf
![]() $\rho _{*}({\mathcal {O}}_{S_0^{\text {nor}}} ^{\times })/{\mathcal {O}}_{S_0}^{\times }$
is a skyscraper sheaf and the residue fields at closed points of
$\rho _{*}({\mathcal {O}}_{S_0^{\text {nor}}} ^{\times })/{\mathcal {O}}_{S_0}^{\times }$
is a skyscraper sheaf and the residue fields at closed points of
![]() ${\mathcal {S}}_0$
are finite fields. The kernel
${\mathcal {S}}_0$
are finite fields. The kernel
![]() $\text {ker}(\text {deg})=\oplus _{r=1}^s \operatorname {Pic} (H_r) \oplus (\oplus _{i=1}^t \operatorname {Pic}^0 (\widetilde E_i))$
of the right lower vertical map is finite:
$\text {ker}(\text {deg})=\oplus _{r=1}^s \operatorname {Pic} (H_r) \oplus (\oplus _{i=1}^t \operatorname {Pic}^0 (\widetilde E_i))$
of the right lower vertical map is finite:
![]() $\operatorname {Pic}^0 (\widetilde E_i)$
is finite since
$\operatorname {Pic}^0 (\widetilde E_i)$
is finite since
![]() $\widetilde E_i$
is a proper and non-singular curve over a finite field, and for
$\widetilde E_i$
is a proper and non-singular curve over a finite field, and for
![]() $1\le r\le s$
it holds
$1\le r\le s$
it holds
![]() $\operatorname {Pic}(H_r)$
is finite since
$\operatorname {Pic}(H_r)$
is finite since
![]() $H_r$
is an affine and normal one-dimensional scheme of finite type over the finite field F. Indeed, assume for simplicity that
$H_r$
is an affine and normal one-dimensional scheme of finite type over the finite field F. Indeed, assume for simplicity that
![]() $H_r$
is geometrically connected over F. Let
$H_r$
is geometrically connected over F. Let
![]() $\ell /F$
be a finite extension such that
$\ell /F$
be a finite extension such that
![]() $U_r\overset {\text {def}} = H_r\times _{\operatorname {Spec} F}\operatorname {Spec} \ell $
admits a smooth and connected compactification
$U_r\overset {\text {def}} = H_r\times _{\operatorname {Spec} F}\operatorname {Spec} \ell $
admits a smooth and connected compactification
![]() $C_r$
with
$C_r$
with
![]() $(C_r\setminus U_r) (\ell )\neq \emptyset $
. Let
$(C_r\setminus U_r) (\ell )\neq \emptyset $
. Let
![]() $U_r\to H_r$
be the canonical morphism, and let
$U_r\to H_r$
be the canonical morphism, and let
![]() $\operatorname {Pic}(H_r)\to \operatorname {Pic} (U_r)$
be the induced map of pullback of line bundles. Then
$\operatorname {Pic}(H_r)\to \operatorname {Pic} (U_r)$
be the induced map of pullback of line bundles. Then
![]() $\operatorname {Ker} [ \operatorname {Pic}(H_r)\to \operatorname {Pic} (U_r)]$
is finite (cf. [Reference Guralnick, Jaffe and Raskind10, Theorem 1.8]). Further, the map
$\operatorname {Ker} [ \operatorname {Pic}(H_r)\to \operatorname {Pic} (U_r)]$
is finite (cf. [Reference Guralnick, Jaffe and Raskind10, Theorem 1.8]). Further, the map
![]() $\operatorname {Pic}^0(C_r)\to \operatorname {Pic} (U_r)$
obtained by restricting a degree
$\operatorname {Pic}^0(C_r)\to \operatorname {Pic} (U_r)$
obtained by restricting a degree
![]() $0$
line bundle on
$0$
line bundle on
![]() $C_r$
to
$C_r$
to
![]() $U_r$
is surjective (if
$U_r$
is surjective (if
![]() $x\in (C_r \setminus U_r)(\ell )$
and
$x\in (C_r \setminus U_r)(\ell )$
and
![]() $D\in \operatorname {Pic} (U_r)$
has degree m then
$D\in \operatorname {Pic} (U_r)$
has degree m then
![]() $D-mx\in \operatorname {Pic}^0(C_r)$
restricts to D on
$D-mx\in \operatorname {Pic}^0(C_r)$
restricts to D on
![]() $U_r$
); hence,
$U_r$
); hence,
![]() $\operatorname {Pic} (U_r)$
is finite since
$\operatorname {Pic} (U_r)$
is finite since
![]() $\operatorname {Pic} ^0(C_r)$
is finite. From the above, it follows that
$\operatorname {Pic} ^0(C_r)$
is finite. From the above, it follows that
![]() $\operatorname {Pic}(H_r)$
is finite.
$\operatorname {Pic}(H_r)$
is finite.
This finishes the proof of Claim 1.
Consider the composite map
Claim 2.
![]() $\text {ker}(\psi _n)$
is finite.
$\text {ker}(\psi _n)$
is finite.
Proof of Claim 2
First, we prove that the kernel of the map
![]() $\operatorname {Pic} ({\mathcal {S}}_n)\to \operatorname {Pic} ({\mathcal {S}}_{n-1})$
is finite for
$\operatorname {Pic} ({\mathcal {S}}_n)\to \operatorname {Pic} ({\mathcal {S}}_{n-1})$
is finite for
![]() $n\ge 2$
. Write
$n\ge 2$
. Write
![]() ${\mathcal {I}}_n$
for the sheaf of ideals of
${\mathcal {I}}_n$
for the sheaf of ideals of
![]() ${\mathcal {O}}_{{\mathcal {S}}}$
defining
${\mathcal {O}}_{{\mathcal {S}}}$
defining
![]() ${\mathcal {S}}_n$
. We have an exact sequence of sheaves on
${\mathcal {S}}_n$
. We have an exact sequence of sheaves on
![]() ${\mathcal {S}}_n$
:
${\mathcal {S}}_n$
:
which induces an exact sequence in cohomology
Further, the truncated exponential map
![]() $\alpha \mapsto 1+\alpha $
induces an isomorphism of sheaves
$\alpha \mapsto 1+\alpha $
induces an isomorphism of sheaves
![]() ${\mathcal {I}}_{n-1}/{\mathcal {I}}_n\overset \sim \to 1+({\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
[
${\mathcal {I}}_{n-1}/{\mathcal {I}}_n\overset \sim \to 1+({\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
[
![]() $({\mathcal {I}}_{n-1}/{\mathcal {I}}_n)^2=0$
]; hence,
$({\mathcal {I}}_{n-1}/{\mathcal {I}}_n)^2=0$
]; hence,
![]() $H^2({\mathcal {S}}_n,1+{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)=0$
and the map
$H^2({\mathcal {S}}_n,1+{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)=0$
and the map
![]() $\operatorname {Pic}({\mathcal {S}}_n)\to \operatorname {Pic}({\mathcal {S}}_{n-1})$
is surjective. Moreover,
$\operatorname {Pic}({\mathcal {S}}_n)\to \operatorname {Pic}({\mathcal {S}}_{n-1})$
is surjective. Moreover,
![]() $H^1({\mathcal {S}}_n,{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
is finite. Indeed,
$H^1({\mathcal {S}}_n,{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
is finite. Indeed,
![]() $H^1({\mathcal {S}}_n,{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
is a finitely generated
$H^1({\mathcal {S}}_n,{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
is a finitely generated
![]() $B_n$
-module with finite support since the morphism
$B_n$
-module with finite support since the morphism
![]() $\lambda _n^{-1}({\mathcal {Z}}_n\setminus \{z_1,\ldots ,z_t\})\to {\mathcal {Z}}_n\setminus \{z_1,\ldots ,z_t\}$
is affine and
$\lambda _n^{-1}({\mathcal {Z}}_n\setminus \{z_1,\ldots ,z_t\})\to {\mathcal {Z}}_n\setminus \{z_1,\ldots ,z_t\}$
is affine and
![]() $R^1(\pi _n)_{*}({\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
is the sheaf associated with the
$R^1(\pi _n)_{*}({\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
is the sheaf associated with the
![]() $B_n$
-module
$B_n$
-module
![]() $H^1({\mathcal {S}}_n,{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
; here,
$H^1({\mathcal {S}}_n,{\mathcal {I}}_{n-1}/{\mathcal {I}}_n)$
; here,
![]() $\lambda _n:{\mathcal {S}}_n\to {\mathcal {Z}}_n$
is the proper morphism induced by
$\lambda _n:{\mathcal {S}}_n\to {\mathcal {Z}}_n$
is the proper morphism induced by
![]() $\lambda $
. This shows that the kernel of the map
$\lambda $
. This shows that the kernel of the map
![]() $\operatorname {Pic} ({\mathcal {S}}_n)\to \operatorname {Pic} ({\mathcal {S}}_{n-1})$
is finite for all
$\operatorname {Pic} ({\mathcal {S}}_n)\to \operatorname {Pic} ({\mathcal {S}}_{n-1})$
is finite for all
![]() $n\ge 2$
. A similar argument shows that the kernel of the map
$n\ge 2$
. A similar argument shows that the kernel of the map
![]() $\operatorname {Pic} ({\mathcal {S}}_1)\to \operatorname {Pic} ({\mathcal {S}}_{0})$
is finite. Hence, using Claim 1,
$\operatorname {Pic} ({\mathcal {S}}_1)\to \operatorname {Pic} ({\mathcal {S}}_{0})$
is finite. Hence, using Claim 1,
![]() $\text {ker}(\psi _n)$
is finite.
$\text {ker}(\psi _n)$
is finite.
This finishes the proof of Claim 2.
In light of Claim 2, and in order to prove assertion (A), it suffices to prove that the cokernel of the composite map
is finite. The latter follows from the nondegeneracy of the intersection pairing
![]() $(\oplus _{j=1}^{n_i}\mathbb {Z})\times (\oplus _{j=1}^{n_i}\mathbb {Z})\to \mathbb {Z}$
on each fiber
$(\oplus _{j=1}^{n_i}\mathbb {Z})\times (\oplus _{j=1}^{n_i}\mathbb {Z})\to \mathbb {Z}$
on each fiber
![]() $E_i$
(cf. [Reference Shafarevich26, Lemma on page 69 and the discussion on page 71 after this lemma]),
$E_i$
(cf. [Reference Shafarevich26, Lemma on page 69 and the discussion on page 71 after this lemma]),
![]() $1\le i\le t$
.
$1\le i\le t$
.
This finishes the proof of assertion (A).
Proof of assertion (B)
Let
![]() ${\mathcal {J}}$
be an ample invertible
${\mathcal {J}}$
be an ample invertible
![]() ${\mathcal {O}}_S$
-ideal such that
${\mathcal {O}}_S$
-ideal such that
![]() $\text {Supp} ({\mathcal {O}}_S/{\mathcal {J}})={\mathcal {S}}_0$
. The existence of such
$\text {Supp} ({\mathcal {O}}_S/{\mathcal {J}})={\mathcal {S}}_0$
. The existence of such
![]() ${\mathcal {J}}$
follows from the facts that
${\mathcal {J}}$
follows from the facts that
![]() $H_r$
is affine (cf. Proof of Assertion A),
$H_r$
is affine (cf. Proof of Assertion A),
![]() $1\le r\le s$
, the intersection pairing
$1\le r\le s$
, the intersection pairing
![]() $(\oplus _{j=1}^{n_i}\mathbb {Z})\times (\oplus _{j=1}^{n_i}\mathbb {Z})\to \mathbb {Z}$
on each fiber
$(\oplus _{j=1}^{n_i}\mathbb {Z})\times (\oplus _{j=1}^{n_i}\mathbb {Z})\to \mathbb {Z}$
on each fiber
![]() $E_i$
is negative definite (cf. [Reference Shafarevich26, Lemma on page 69 and the discussion on page 71 after this lemma]), and the numerical criterion of ampleness on curves. More precisely,
$E_i$
is negative definite (cf. [Reference Shafarevich26, Lemma on page 69 and the discussion on page 71 after this lemma]), and the numerical criterion of ampleness on curves. More precisely,
![]() $\forall \ 1\le i\le t$
, one can find a divisor
$\forall \ 1\le i\le t$
, one can find a divisor
![]() $D=\sum _{ j=1}^{n_i}m_{ij} D_{i,j}$
with
$D=\sum _{ j=1}^{n_i}m_{ij} D_{i,j}$
with
![]() $m_{i,j}<0$
and
$m_{i,j}<0$
and
![]() $D.D_{i,j}> 0$
for all
$D.D_{i,j}> 0$
for all
![]() $1\le j \le n_j$
.
$1\le j \le n_j$
.
For
![]() $m\ge 1$
, let
$m\ge 1$
, let
![]() ${\mathcal {S}}^{\prime }_m$
be the closed subscheme of
${\mathcal {S}}^{\prime }_m$
be the closed subscheme of
![]() ${\mathcal {S}}$
defined by the sheaf of ideals
${\mathcal {S}}$
defined by the sheaf of ideals
![]() ${\mathcal {J}}^m$
. To prove Assertion B, it suffices to prove that there exists
${\mathcal {J}}^m$
. To prove Assertion B, it suffices to prove that there exists
![]() $m_0>0$
such that the map
$m_0>0$
such that the map
is an isomorphism for any
![]() $m>m_0$
. We have an exact sequence of shaves on
$m>m_0$
. We have an exact sequence of shaves on
![]() ${\mathcal {S}}^{\prime }_{m+1}$
:
${\mathcal {S}}^{\prime }_{m+1}$
:
where the map
![]() ${\mathcal {J}}^{m}/{\mathcal {J}}^{m+1}\to {\mathcal {O}}_{S^{\prime }_{m+1}}^{\times }$
maps a local section
${\mathcal {J}}^{m}/{\mathcal {J}}^{m+1}\to {\mathcal {O}}_{S^{\prime }_{m+1}}^{\times }$
maps a local section
![]() $\alpha $
to
$\alpha $
to
![]() $1+\alpha $
, which induces an exact sequence in cohomology
$1+\alpha $
, which induces an exact sequence in cohomology
Now, there exists
![]() $m_0>0$
such that
$m_0>0$
such that
![]() $H^1({\mathcal {S}}^{\prime }_{m+1},{\mathcal {J}}^{m}/{\mathcal {J}}^{m+1})=0$
if
$H^1({\mathcal {S}}^{\prime }_{m+1},{\mathcal {J}}^{m}/{\mathcal {J}}^{m+1})=0$
if
![]() $m\ge m_0$
by [Reference Grothendieck and Dieudonné9, première partie, Proposition 2.2.1].
$m\ge m_0$
by [Reference Grothendieck and Dieudonné9, première partie, Proposition 2.2.1].
This finishes the proof of assertion (B).
This finishes the proof of Proposition 4.1.
5 Compactification of formal germs of p-adic curves
In this section, we use the following notations: K is a complete discrete valuation field with valuation ring R, uniformizing parameter
![]() $\pi $
, and with perfect residue field
$\pi $
, and with perfect residue field
![]() $\ell \overset {\text {def}} = R/\pi R$
. Further, A is a two-dimensional normal complete local ring containing R with maximal ideal
$\ell \overset {\text {def}} = R/\pi R$
. Further, A is a two-dimensional normal complete local ring containing R with maximal ideal
![]() ${\mathfrak {m}}_A$
containing
${\mathfrak {m}}_A$
containing
![]() $\pi $
and residue field
$\pi $
and residue field
![]() $\ell =A/{{\mathfrak {m}}}_A$
. We assume that
$\ell =A/{{\mathfrak {m}}}_A$
. We assume that
![]() $X\overset {\text {def}} = \operatorname {Spec} (A\otimes _RK)$
is geometrically connected. Given a finite extension
$X\overset {\text {def}} = \operatorname {Spec} (A\otimes _RK)$
is geometrically connected. Given a finite extension
![]() $L/K$
, we write
$L/K$
, we write
![]() ${\mathcal {O}}_L$
for the valuation ring of L,
${\mathcal {O}}_L$
for the valuation ring of L,
![]() $A_L\overset {\text {def}} = A\otimes _{{\mathcal {O}}_L}L$
,
$A_L\overset {\text {def}} = A\otimes _{{\mathcal {O}}_L}L$
,
![]() $A_{{\mathcal {O}}_L}\overset {\text {def}} = A\otimes _R{{\mathcal {O}}_L}$
, and
$A_{{\mathcal {O}}_L}\overset {\text {def}} = A\otimes _R{{\mathcal {O}}_L}$
, and
![]() $A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
the normalization of
$A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
the normalization of
![]() $A_{{\mathcal {O}}_L}$
in its total ring of fractions.
$A_{{\mathcal {O}}_L}$
in its total ring of fractions.
Proposition 5.1 (Compactification of formal germs of p-adic curves)
We use the above notations. There exists a finite extension
![]() $L/K$
, a flat, proper, connected, and normal
$L/K$
, a flat, proper, connected, and normal
![]() ${\mathcal {O}}_L$
-relative curve
${\mathcal {O}}_L$
-relative curve
![]() ${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_L$
, a closed point
${\mathcal {Y}}\to \operatorname {Spec} {\mathcal {O}}_L$
, a closed point
![]() $y\in {\mathcal {Y}}$
, and an isomorphism
$y\in {\mathcal {Y}}$
, and an isomorphism
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
where
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
where
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}$
is the completion of the local ring
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}$
is the completion of the local ring
![]() ${\mathcal {O}}_{{\mathcal {Y}},y}$
of
${\mathcal {O}}_{{\mathcal {Y}},y}$
of
![]() ${\mathcal {Y}}$
at y.
${\mathcal {Y}}$
at y.
Proof. By the main result in [Reference Epp4, Introduction], there exists a finite extension
![]() $L/K$
with uniformizing parameter
$L/K$
with uniformizing parameter
![]() $\pi _L$
such that
$\pi _L$
such that
![]() $A_{{\mathcal {O}}_L}^{\operatorname {nor}}/\pi _LA_{{\mathcal {O}}_L}^{\operatorname {nor}}$
is reduced. Note that
$A_{{\mathcal {O}}_L}^{\operatorname {nor}}/\pi _LA_{{\mathcal {O}}_L}^{\operatorname {nor}}$
is reduced. Note that
![]() $A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
is a normal two-dimensional complete local ring with perfect residue field (cf. [Reference Bourbaki2, Chap. IX, §4, Lemma 1] and our assumption that X is geometrically connected). Without loss of generality, we will assume that
$A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
is a normal two-dimensional complete local ring with perfect residue field (cf. [Reference Bourbaki2, Chap. IX, §4, Lemma 1] and our assumption that X is geometrically connected). Without loss of generality, we will assume that
![]() $A/\pi A$
is reduced. We show that there exist a proper, flat, connected, and normal relative R-curve
$A/\pi A$
is reduced. We show that there exist a proper, flat, connected, and normal relative R-curve
![]() ${\mathcal {Y}}\to \operatorname {Spec} R$
, a closed point
${\mathcal {Y}}\to \operatorname {Spec} R$
, a closed point
![]() $y\in {\mathcal {Y}}$
, and an isomorphism
$y\in {\mathcal {Y}}$
, and an isomorphism
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
.
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
.
First,
![]() $A/\pi A$
is a (reduced) one-dimensional complete local ring with residue field
$A/\pi A$
is a (reduced) one-dimensional complete local ring with residue field
![]() $\ell $
, hence is isomorphic to a quotient
$\ell $
, hence is isomorphic to a quotient
![]() $\ell [[x_1,\ldots ,x_t]]/{\mathfrak {a}}$
of a formal power series ring
$\ell [[x_1,\ldots ,x_t]]/{\mathfrak {a}}$
of a formal power series ring
![]() $\ell [[x_1,\ldots ,x_t]]$
over
$\ell [[x_1,\ldots ,x_t]]$
over
![]() $\ell $
(cf. [Reference Bourbaki2, chapitre IX, §3]). It then follows from [Reference Artin1, Theorem 3.8] and basic facts on the theory of algebraic curves, that there exist a proper and reduced connected (but not necessarily irreducible)
$\ell $
(cf. [Reference Bourbaki2, chapitre IX, §3]). It then follows from [Reference Artin1, Theorem 3.8] and basic facts on the theory of algebraic curves, that there exist a proper and reduced connected (but not necessarily irreducible)
![]() $\ell $
-curve Z, a closed point
$\ell $
-curve Z, a closed point
![]() $y\in Z$
, and an isomorphism
$y\in Z$
, and an isomorphism
![]() $\hat {\mathcal {O}}_{Z,y}\overset \sim \to A/\pi A$
where
$\hat {\mathcal {O}}_{Z,y}\overset \sim \to A/\pi A$
where
![]() $\hat {\mathcal {O}}_{Z,y}$
is the completion of the local ring
$\hat {\mathcal {O}}_{Z,y}$
is the completion of the local ring
![]() ${\mathcal {O}}_{Z,y}$
of Z at y. Moreover, Z is non-singular outside y. There exists a rational function f on Z which defines a finite generically separable morphism
${\mathcal {O}}_{Z,y}$
of Z at y. Moreover, Z is non-singular outside y. There exists a rational function f on Z which defines a finite generically separable morphism
![]() $f:Z\to \Bbb P^1_{\ell }$
such that
$f:Z\to \Bbb P^1_{\ell }$
such that
![]() $y=f^{-1}(\infty )$
(cf. [Reference Harbater and Stevenson12, Proof of Theorem 3]). Thus, by considering the completion of the morphism f above
$y=f^{-1}(\infty )$
(cf. [Reference Harbater and Stevenson12, Proof of Theorem 3]). Thus, by considering the completion of the morphism f above
![]() $\infty $
, we obtain a finite generically separable morphism
$\infty $
, we obtain a finite generically separable morphism
![]() $\bar g:\operatorname {Spec} (A/\pi A)\to \operatorname {Spec} (\ell [[t]])$
where t is a local parameter at
$\bar g:\operatorname {Spec} (A/\pi A)\to \operatorname {Spec} (\ell [[t]])$
where t is a local parameter at
![]() $\infty $
. This morphism lifts to a finite morphism
$\infty $
. This morphism lifts to a finite morphism
![]() $g:\operatorname {Spf} A\to \operatorname {Spf} (R[[T]])$
of formal schemes (cf. [Reference Harbater and Stevenson12, Lemma 2]). Let
$g:\operatorname {Spf} A\to \operatorname {Spf} (R[[T]])$
of formal schemes (cf. [Reference Harbater and Stevenson12, Lemma 2]). Let
![]() $\widetilde Z\to Z$
be the morphism of normalization, and let
$\widetilde Z\to Z$
be the morphism of normalization, and let
![]() $\{x_1,\ldots ,x_m\}\subset \widetilde Z$
be the pre-image of y. There is a one-to-one correspondence between the set
$\{x_1,\ldots ,x_m\}\subset \widetilde Z$
be the pre-image of y. There is a one-to-one correspondence between the set
![]() $\{\mathfrak {p}_1,\ldots ,\mathfrak {p}_m\}\subset \operatorname {Spec} A$
of prime ideals of height
$\{\mathfrak {p}_1,\ldots ,\mathfrak {p}_m\}\subset \operatorname {Spec} A$
of prime ideals of height
![]() $1$
containing
$1$
containing
![]() $\pi $
and the set
$\pi $
and the set
![]() $\{x_1,\ldots ,x_m\}$
,
$\{x_1,\ldots ,x_m\}$
,
![]() $\mathfrak {p}_i$
corresponds to
$\mathfrak {p}_i$
corresponds to
![]() $x_i$
,
$x_i$
,
![]() $1\le i\le m$
. The composite morphism
$1\le i\le m$
. The composite morphism
![]() $\widetilde Z\to Z\to \Bbb P^1_{\ell }$
induces, by completion above
$\widetilde Z\to Z\to \Bbb P^1_{\ell }$
induces, by completion above
![]() $\infty $
, finite separable morphisms
$\infty $
, finite separable morphisms
![]() $\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
where
$\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
where
![]() $\operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})$
is the fraction field of the completion
$\operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})$
is the fraction field of the completion
![]() $\hat {\mathcal {O}}_{\widetilde Z,x_i}$
of the local ring
$\hat {\mathcal {O}}_{\widetilde Z,x_i}$
of the local ring
![]() ${\mathcal {O}}_{\widetilde Z,x_i}$
of
${\mathcal {O}}_{\widetilde Z,x_i}$
of
![]() $\widetilde Z$
at
$\widetilde Z$
at
![]() $x_i$
,
$x_i$
,
![]() $1\le i\le m$
(with the above notations
$1\le i\le m$
(with the above notations
![]() $t=T \quad\mod \pi $
).
$t=T \quad\mod \pi $
).
Consider the formal closed unit disk
![]() $D=\operatorname {Spf} R<\frac {1}{T}>$
with parameter
$D=\operatorname {Spf} R<\frac {1}{T}>$
with parameter
![]() $\frac {1}{T}$
and its special fiber
$\frac {1}{T}$
and its special fiber
![]() $D_{\ell }=\operatorname {Spec} \ell [\frac {1}{t}]$
(
$D_{\ell }=\operatorname {Spec} \ell [\frac {1}{t}]$
(
![]() $D_{\ell } \overset \sim \to \Bbb A^1_{\ell }$
). By a result of Gabber and Katz (cf. [Reference Katz14, Main Theorem 1.4.1]), there exists, for
$D_{\ell } \overset \sim \to \Bbb A^1_{\ell }$
). By a result of Gabber and Katz (cf. [Reference Katz14, Main Theorem 1.4.1]), there exists, for
![]() $1\le i\le m$
, a finite cover
$1\le i\le m$
, a finite cover
![]() $\bar h_i:C_i\to D_{\ell }$
with
$\bar h_i:C_i\to D_{\ell }$
with
![]() $C_i$
connected, which only (tamely) ramifies above the point
$C_i$
connected, which only (tamely) ramifies above the point
![]() $\frac {1}{t}=0$
and such that the completion of
$\frac {1}{t}=0$
and such that the completion of
![]() $\bar h_i$
above
$\bar h_i$
above
![]() $t=0$
is generically isomorphic to the cover
$t=0$
is generically isomorphic to the cover
![]() $\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
. Using formal patching techniques (cf. [Reference Saïdi23, 1.2]), one can lift the covers
$\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
. Using formal patching techniques (cf. [Reference Saïdi23, 1.2]), one can lift the covers
![]() $\bar h_i$
to finite covers
$\bar h_i$
to finite covers
![]() $h_i:Y_i\to D$
which only ramify above the point
$h_i:Y_i\to D$
which only ramify above the point
![]() $\frac {1}{T}=0$
,
$\frac {1}{T}=0$
,
![]() $1\le i\le m$
. (Outside
$1\le i\le m$
. (Outside
![]() $\frac {1}{T}=0$
, the existence of such a lifting follows from the theorems of lifting of étale covers [cf. [Reference Grothendieck8, Exposé I, Corollaire 8.4]]. In a formal neighborhood of
$\frac {1}{T}=0$
, the existence of such a lifting follows from the theorems of lifting of étale covers [cf. [Reference Grothendieck8, Exposé I, Corollaire 8.4]]. In a formal neighborhood of
![]() $\frac {1}{T}=0$
, such a lifting is possible under the tameness condition: étale locally near
$\frac {1}{T}=0$
, such a lifting is possible under the tameness condition: étale locally near
![]() $\frac {1}{t}$
the cover
$\frac {1}{t}$
the cover
![]() $\bar h_i$
is defined by an equation
$\bar h_i$
is defined by an equation
![]() $y^s=\frac {1}{t^e}$
, where
$y^s=\frac {1}{t^e}$
, where
![]() $s\ge 1$
is an integer prime to the characteristic of
$s\ge 1$
is an integer prime to the characteristic of
![]() $\ell $
, and one lifts to the cover defined by
$\ell $
, and one lifts to the cover defined by
![]() $Y^s=\frac {1}{T^e}$
.) For
$Y^s=\frac {1}{T^e}$
.) For
![]() $1\le i\le m$
, let
$1\le i\le m$
, let
![]() $\hat A_{\mathfrak {p}_i}$
be the completion of the localization
$\hat A_{\mathfrak {p}_i}$
be the completion of the localization
![]() $A_{\mathfrak {p}_i}$
of A at
$A_{\mathfrak {p}_i}$
of A at
![]() ${\mathfrak {p}}_i$
. Thus,
${\mathfrak {p}}_i$
. Thus,
![]() $\hat A_{\mathfrak {p}_i}$
is a complete discrete valuation ring with uniformizing parameter
$\hat A_{\mathfrak {p}_i}$
is a complete discrete valuation ring with uniformizing parameter
![]() $\pi $
(recall
$\pi $
(recall
![]() $A/\pi A$
is reduced) and residue field
$A/\pi A$
is reduced) and residue field
![]() $\operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})$
. Let B be the completion of the localization of
$\operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})$
. Let B be the completion of the localization of
![]() $R[[T]]$
at
$R[[T]]$
at
![]() $\pi $
. Thus, B is a complete discrete valuation ring with residue field
$\pi $
. Thus, B is a complete discrete valuation ring with residue field
![]() $\ell ((t))$
. The finite cover
$\ell ((t))$
. The finite cover
![]() $g:\operatorname {Spf} A\to \operatorname {Spf} (R[[T]])$
induces, by pullback to
$g:\operatorname {Spf} A\to \operatorname {Spf} (R[[T]])$
induces, by pullback to
![]() $\operatorname {Spf} B$
, finite covers
$\operatorname {Spf} B$
, finite covers
![]() $g_i:\operatorname {Spf} \hat A_{\mathfrak {p}_i}\to \operatorname {Spf} B$
which (by construction) lift the covers
$g_i:\operatorname {Spf} \hat A_{\mathfrak {p}_i}\to \operatorname {Spf} B$
which (by construction) lift the covers
![]() $\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
,
$\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
,
![]() $1\le i\le m$
. Further, the cover
$1\le i\le m$
. Further, the cover
![]() $h_i:Y_i\to D$
induces, by pullback to
$h_i:Y_i\to D$
induces, by pullback to
![]() $\operatorname {Spf} B$
, a finite cover
$\operatorname {Spf} B$
, a finite cover
![]() $\tilde h_i:\operatorname {Spf} B_i\to \operatorname {Spf} B$
which by construction lifts the cover
$\tilde h_i:\operatorname {Spf} B_i\to \operatorname {Spf} B$
which by construction lifts the cover
![]() $\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
. Thus, the covers
$\bar g_i:\operatorname {Spec} \operatorname {Fr} (\hat {\mathcal {O}}_{\widetilde Z,x_i})\to \operatorname {Spec} \ell ((t))$
. Thus, the covers
![]() $\tilde h_i:\operatorname {Spf} B_i\to \operatorname {Spf} B$
and
$\tilde h_i:\operatorname {Spf} B_i\to \operatorname {Spf} B$
and
![]() $g_i:\operatorname {Spf} \hat A_{\mathfrak {p}_i}\to \operatorname {Spf} B$
are isomorphic since
$g_i:\operatorname {Spf} \hat A_{\mathfrak {p}_i}\to \operatorname {Spf} B$
are isomorphic since
![]() $\bar g_i$
is generically separable. Using formal patching techniques (cf. [Reference Grothendieck8, Exposé I, Corollaire 8.4]), one can patch the covers
$\bar g_i$
is generically separable. Using formal patching techniques (cf. [Reference Grothendieck8, Exposé I, Corollaire 8.4]), one can patch the covers
![]() $g:\operatorname {Spf} A\to \operatorname {Spf} (R[[T]])$
and
$g:\operatorname {Spf} A\to \operatorname {Spf} (R[[T]])$
and
![]() $h_i:Y_i\to D$
,
$h_i:Y_i\to D$
,
![]() $1\le i\le m$
, to construct a finite cover
$1\le i\le m$
, to construct a finite cover
![]() ${\mathcal {Y}}\to \Bbb P^1_{R}$
in the category of formal schemes with
${\mathcal {Y}}\to \Bbb P^1_{R}$
in the category of formal schemes with
![]() ${\mathcal {Y}}$
normal, connected, proper, and flat over
${\mathcal {Y}}$
normal, connected, proper, and flat over
![]() $\operatorname {Spf} R$
. The special fiber
$\operatorname {Spf} R$
. The special fiber
![]() ${\mathcal {Y}}_{\ell }\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} R}\operatorname {Spec} \ell $
of
${\mathcal {Y}}_{\ell }\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} R}\operatorname {Spec} \ell $
of
![]() ${\mathcal {Y}}$
consists of m irreducible components which intersect at the point y and is (by construction) non-singular outside y. The formal curve
${\mathcal {Y}}$
consists of m irreducible components which intersect at the point y and is (by construction) non-singular outside y. The formal curve
![]() ${\mathcal {Y}}$
is algebraic by formal GAGA and (by construction)
${\mathcal {Y}}$
is algebraic by formal GAGA and (by construction)
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
as required.
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
as required.
Remark 5.2. Proposition 5.1 asserts the existence, after possibly a finite extension of K, of a proper R-curve
![]() ${\mathcal {Y}}$
and a closed point
${\mathcal {Y}}$
and a closed point
![]() $y\in {\mathcal {Y}}^{\operatorname {cl}}$
such that
$y\in {\mathcal {Y}}^{\operatorname {cl}}$
such that
![]() $\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
. The special fiber
$\hat {\mathcal {O}}_{{\mathcal {Y}},y}\overset \sim \to A$
. The special fiber
![]() ${\mathcal {Y}}_{\ell }\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} R}\operatorname {Spec} \ell $
of
${\mathcal {Y}}_{\ell }\overset {\text {def}} = {\mathcal {Y}}\times _{\operatorname {Spec} R}\operatorname {Spec} \ell $
of
![]() ${\mathcal {Y}}$
consists of
${\mathcal {Y}}$
consists of
![]() $m_y\overset {\text {def}} = m$
(cf. the proof of Proposition 5.1 for the definition of m) irreducible components
$m_y\overset {\text {def}} = m$
(cf. the proof of Proposition 5.1 for the definition of m) irreducible components
![]() $\{C_1,\ldots ,C_m\}$
which intersect at y,
$\{C_1,\ldots ,C_m\}$
which intersect at y,
![]() ${\mathcal {Y}}_{\ell }$
is non-singular outside y, and the normalization morphism
${\mathcal {Y}}_{\ell }$
is non-singular outside y, and the normalization morphism
![]() $C_i^{\operatorname {nor}}\to C_i$
is a homeomorphism,
$C_i^{\operatorname {nor}}\to C_i$
is a homeomorphism,
![]() $1\le i\le m$
. In fact, one can, assuming the existence of a compactification of
$1\le i\le m$
. In fact, one can, assuming the existence of a compactification of
![]() $\operatorname {Spec} A$
as in Proposition 5.1, construct such a compactification
$\operatorname {Spec} A$
as in Proposition 5.1, construct such a compactification
![]() ${\mathcal {Y}}$
of
${\mathcal {Y}}$
of
![]() $\operatorname {Spec} A$
with the additional property that
$\operatorname {Spec} A$
with the additional property that
![]() $C_i^{\operatorname {nor}}\overset \sim \to \Bbb P^1_{\ell }$
,
$C_i^{\operatorname {nor}}\overset \sim \to \Bbb P^1_{\ell }$
,
![]() $\forall 1\le i\le m$
(cf. [Reference Saïdi23, Remark 3.1]).
$\forall 1\le i\le m$
(cf. [Reference Saïdi23, Remark 3.1]).
Proposition 5.3. We use the above notations. There exist a finite extension
![]() $L/K$
and a finite morphism
$L/K$
and a finite morphism
![]() $\operatorname {Spec} B\to \operatorname {Spec} A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
with B local, normal, hyperbolic (cf. Notations), and the morphism
$\operatorname {Spec} B\to \operatorname {Spec} A_{{\mathcal {O}}_L}^{\operatorname {nor}}$
with B local, normal, hyperbolic (cf. Notations), and the morphism
![]() $\operatorname {Spec} B_L\to \operatorname {Spec} A_L$
is geometric and étale.
$\operatorname {Spec} B_L\to \operatorname {Spec} A_L$
is geometric and étale.
Proof. This follows easily from Proposition 5.1, Remark 5.2, and Theorem 3 in [Reference Saïdi23].
Acknowledgments
I would like to thank Akio Tamagawa for several discussions we had on the topic of this paper. I would like to thank the referee for his/her careful reading of the paper and comments.