Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-08T03:26:20.647Z Has data issue: false hasContentIssue false
  • English
  • Français

Topics on symbolic Rees algebras for space monomial curves

Published online by Cambridge University Press:  22 January 2016

Shiro Goto ,
Koji Nishida  and
Yasuhiro Shimoda
Shiro Goto
Affiliation:
Department of Mathematics, School of Science and Technology Meiji University, Higashimita, Tama-ku Kawasaki-shi 214, Japan
Koji Nishida
Affiliation:
Department of Mathematics, Faculty of Science Chiba University, Yayoi-cho, Chiba-shi 260, Japan
Yasuhiro Shimoda
Affiliation:
College of Liberal Arts and Sciences Kitasato University, Kitasato, Sagamihara-shi 228, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

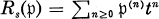Let A be a regular local ring of dim A = 3 and p a prime ideal in A of dim A/p = 1. We put Rs(p) = (here t denotes an indeterminate over A) and call it the symbolic Rees algebra of p. With this notation the authors [5, 6] investigated the condition under which the A-algebra Rs(p) is Cohen-Macaulay and gave a criterion for Rs(p) to be a Gorenstein ring in terms of the elements f and g in Huneke’s condition [11, Theorem 3.1] of Rs(p) being Noetherian. They furthermore explored the prime ideals p = p(n1, n2, n3) in the formal power series ring A = k[X, Y, Z] over a field k defining space monomial curves 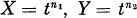and Z = 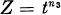with GCD(n1, n2, nz) = 1 and proved that Rs(p) are Gorenstein rings for certain prime ideals p = p(n1 n2, n3). In the present research, similarly as in [5, 6], we are interested in the ring-theoretic properties of Rs(p) mainly for p = p(n1 n2) nz) and the results of [5, 6] will play key roles in this paper.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 124 , December 1991 , pp. 99 - 132
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1991

References

[ 1 ] Buchsbaum, D. A. and Eisenbud, D., What makes a complex exact?, J. Alg., 25 (1973), 259–268.Google Scholar
[ 2 ] Buchsbaum, D. A. and Eisenbud, D., Algebra structures for finite free resolutions and structure theorems for ideals of codimension 3, Amer. J. Math., 99 (1977), 447–485.CrossRefGoogle Scholar
[ 3 ] Burch, L., Codimension and analytic spread, Proc. Camb. Phil. Soc, 72 (1972), 369–373.CrossRefGoogle Scholar
[ 4 ] Goto, S., Herrmann, M., Nishida, K. and Villamayor, O., On the structure of Noetherian symbolic Rees algebras, manuscripta math., 67 (1990), 197–225.Google Scholar
[ 5 ] Goto, S., Nishida, K. and Shimoda, Y., The Gorensteinness of symbolic Rees algebras for space curves, J. Math. Soc. Japan, 43 (1991), 465–481.Google Scholar
[ 6 ] Goto, S., Nishida, K. and Shimoda, Y., The Gorensteinness of the symbolic blow-ups for certain space monomial curves, to appear in Trans. Amer. Math. Soc.Google Scholar
[ 7 ] Herzog, J., Generators and relations of abelian semigroups and semigroup rings, manuscripta math., 3 (1970), 175–193.CrossRefGoogle Scholar
[ 8 ] Herzog, J. and Kunz, E., Der kanonische Modul eines Cohen-Macaulay-Rings, Lecture Notes in Math., 238, Springer (1971).CrossRefGoogle Scholar
[ 9 ] Herzog, J. and Ulrich, B., Self-linked curve singularities, Nagoya Math. J., 120 (1990), 129–153.Google Scholar
[10] Huckaba, S., Analytic spread modulo an element and symbolic Rees algebras, J. Algebra, 128 (1990), 306–320.CrossRefGoogle Scholar
[11] Huneke, C., Hilbert functions and symbolic powers, Michigan Math. J., 34 (1987), 293–318.CrossRefGoogle Scholar
[12] Huneke, C, The primary components of and integral closures of ideals in 3-dimensional regular local rings, Math. Ann., 275 (1986), 617–635.CrossRefGoogle Scholar
[13] Huneke, C, On the finite generation of symbolic blow-ups, Math. Z., 179 (1982), 465–472.Google Scholar
[14] McAdam, S., Asymptotic prime divisors, Lecture Notes in Math., 1023, Springer (1983).Google Scholar
[15] Morimoto, M. and Goto, S., Non-Cohen-Macaulay symbolic blow-ups for space monomial curves, to appear in Proc. Amer. Math. Soc.Google Scholar
[16] Peskine, C. and Szpiro, L., Liaison des variétés algébliques. I., Invent Math., 26 (1975), 271–302.Google Scholar
[17] Sally, J., Numbers of generators of ideals in local rings, Lecture Notes in Pure and Appl. Math., 35, Marcel Dekker (1978).Google Scholar
[18] Serre, J. P., Algèbre Locale: Multiplicités (third edition), Lecture Notes in Math., 11, Springer Verlag (1975).Google Scholar
[19] Schenzel, P., Examples of Noetherian symbolic blow-up rings, Rev. Roumaine Math. Pures Appl., 33 (1988), 4, 375–383.Google Scholar
[20] Simis, A. and Trung, N. V., The divisor class group of ordinary and symbolic blow-ups, Math. Z., 198 (1988), 479–491.CrossRefGoogle Scholar
[21] Valla, G., On the symmetric and Rees algebras of an ideal, manuscripta math., 30 (1980), 239–255.CrossRefGoogle Scholar