Research Article
Rees algebras of non-singular equimultiple prime ideals*
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-12
-
- Article
-
- You have access
- Export citation
Modified defect relations for the gauss map of minimal surfaces, III
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-40
-
- Article
-
- You have access
- Export citation
3-dimensional affine hypersurfaces in ℝ4 with parallel cubic form
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-53
-
- Article
-
- You have access
- Export citation
Lattice path proof of the ribbon determinant formula for Schur functions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 55-59
-
- Article
-
- You have access
- Export citation
The stationary phase method with an estimate of the remainder term on a space of large dimension
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 61-97
-
- Article
-
- You have access
- Export citation
Topics on symbolic Rees algebras for space monomial curves
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 99-132
-
- Article
-
- You have access
- Export citation
On S-class number relations of algebraic tori in Galois extensions of global fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 133-144
-
- Article
-
- You have access
- Export citation
Mansfield and Solovay type results on covering plane sets by lines
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 145-155
-
- Article
-
- You have access
- Export citation
On determining certain real quadratic fields with class number one and relating this property to continued fractions and primality properties
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 157-180
-
- Article
-
- You have access
- Export citation
The fundamental unit and bounds for class numbers of real quadratic fields
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 181-197
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 124 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 124 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

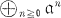 of an equimultiple ideal
of an equimultiple ideal 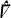 of the affine metric
of the affine metric 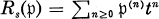 (here
(here 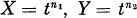 and
and 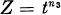 with GCD(
with GCD(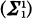 set
set