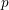1 Introduction
Fix a prime number
![]() $p$
. Let
$p$
. Let
![]() $W$
denote the usual,
$W$
denote the usual,
![]() $p$
-typical Witt vector functor. Let
$p$
-typical Witt vector functor. Let
![]() $R$
be a ring in which
$R$
be a ring in which
![]() $p$
is nilpotent, and write
$p$
is nilpotent, and write
![]() $S=\operatorname{Spec}R$
. Let
$S=\operatorname{Spec}R$
. Let
![]() $W_{n}(S)$
denote
$W_{n}(S)$
denote
![]() $\operatorname{Spec}W_{n}(R)$
, and let
$\operatorname{Spec}W_{n}(R)$
, and let
![]() $W(S)$
denote the direct limit
$W(S)$
denote the direct limit
![]() $\operatorname{colim}_{n}W_{n}(S)$
. We take this limit in the category of sheaves of sets on the category of affine schemes with respect to the étale topology. One could say that
$\operatorname{colim}_{n}W_{n}(S)$
. We take this limit in the category of sheaves of sets on the category of affine schemes with respect to the étale topology. One could say that
![]() $W(S)$
is the correct version of
$W(S)$
is the correct version of
![]() $\operatorname{Spec}W(R)$
, a construction which, as we discuss below, does not have good properties.
$\operatorname{Spec}W(R)$
, a construction which, as we discuss below, does not have good properties.
We say an elliptic curve
![]() $E$
over
$E$
over
![]() $S$
is ordinary when all fibers of
$S$
is ordinary when all fibers of
![]() $E$
, necessarily over points of residue characteristic
$E$
, necessarily over points of residue characteristic
![]() $p$
, are ordinary. For any morphism
$p$
, are ordinary. For any morphism
![]() $f:S^{\prime }\rightarrow S$
, we write
$f:S^{\prime }\rightarrow S$
, we write
![]() $E_{S^{\prime }}$
, or
$E_{S^{\prime }}$
, or
![]() $f^{\ast }(E)$
, for the base change
$f^{\ast }(E)$
, for the base change
![]() $S^{\prime }\times _{S}E$
regarded as an elliptic curve over
$S^{\prime }\times _{S}E$
regarded as an elliptic curve over
![]() $S^{\prime }$
in the evident way.
$S^{\prime }$
in the evident way.
The purpose of this paper is to prove the following:
Theorem . There is a unique way of lifting ordinary elliptic curves
![]() $E$
over affine schemes
$E$
over affine schemes
![]() $S$
on which
$S$
on which
![]() $p$
is nilpotent to elliptic curves
$p$
is nilpotent to elliptic curves
![]() $\widetilde{E}$
over
$\widetilde{E}$
over
![]() $W(S)$
which is compatible with base change in
$W(S)$
which is compatible with base change in
![]() $S$
and has the property that
$S$
and has the property that
![]() $\widetilde{E}$
admits a Frobenius lift
$\widetilde{E}$
admits a Frobenius lift
![]() $\unicode[STIX]{x1D713}:\widetilde{E}\rightarrow F^{\ast }(\widetilde{E})$
, where
$\unicode[STIX]{x1D713}:\widetilde{E}\rightarrow F^{\ast }(\widetilde{E})$
, where
![]() $F$
is the usual Witt vector Frobenius map
$F$
is the usual Witt vector Frobenius map
![]() $F:W(S)\rightarrow W(S)$
.
$F:W(S)\rightarrow W(S)$
.
Note that the requirement here that
![]() $S$
is affine is only to simplify the exposition. We remove it below and allow
$S$
is affine is only to simplify the exposition. We remove it below and allow
![]() $S$
to be any
$S$
to be any
![]() $p$
-adic formal scheme, or even what we call a
$p$
-adic formal scheme, or even what we call a
![]() $p$
-adic sheaf. See Section 4 for the final statement of the theorem and further details.
$p$
-adic sheaf. See Section 4 for the final statement of the theorem and further details.
We call
![]() $\widetilde{E}$
the canonical lift of
$\widetilde{E}$
the canonical lift of
![]() $E$
. In the case
$E$
. In the case
![]() $S=\operatorname{Spec}k$
where
$S=\operatorname{Spec}k$
where
![]() $k$
is a perfect field of characteristic
$k$
is a perfect field of characteristic
![]() $p$
, our canonical lift agrees with the usual one by the remarks in Section 7.1.
$p$
, our canonical lift agrees with the usual one by the remarks in Section 7.1.
We emphasize that not only does this approach to canonical lifts work in much greater generality than previous ones, but it is also essentially formal. For remarks on theories of canonical lifts in completely general contexts, see the epilogue in Section 7.4.
2 Background on sheaves
In this section and the next, we define
![]() $W(S)$
, the infinite-length Witt vector construction when
$W(S)$
, the infinite-length Witt vector construction when
![]() $S$
is a scheme, and even when
$S$
is a scheme, and even when
![]() $S$
is more general. The reason there is something to do is that while
$S$
is more general. The reason there is something to do is that while
![]() $\operatorname{Spec}W_{n}(R)$
is a well-behaved construction, the naive infinite-length analogue
$\operatorname{Spec}W_{n}(R)$
is a well-behaved construction, the naive infinite-length analogue
![]() $\operatorname{Spec}W(R)$
is not. For instance, some basic geometric facts like the theorem in Section 3.2 are not true for the naive construction. Thus, to handle Witt vectors of infinite length geometrically, one needs some way of retaining the information of the projective system of the
$\operatorname{Spec}W(R)$
is not. For instance, some basic geometric facts like the theorem in Section 3.2 are not true for the naive construction. Thus, to handle Witt vectors of infinite length geometrically, one needs some way of retaining the information of the projective system of the
![]() $W_{n}(R)$
instead of crudely passing to the limit
$W_{n}(R)$
instead of crudely passing to the limit
![]() $W(R)=\lim _{n}W_{n}(R)$
in the category of rings.
$W(R)=\lim _{n}W_{n}(R)$
in the category of rings.
One standard way of doing this is to view
![]() $W(R)$
as a topological ring with the inverse-limit topology, each
$W(R)$
as a topological ring with the inverse-limit topology, each
![]() $W_{n}(R)$
being discrete. In the special case where
$W_{n}(R)$
being discrete. In the special case where
![]() $R$
is a perfect
$R$
is a perfect
![]() $\mathbb{F}_{p}$
-algebra, this topology is an adic topology with ideal of definition generated by
$\mathbb{F}_{p}$
-algebra, this topology is an adic topology with ideal of definition generated by
![]() $p$
. We can therefore consider its formal spectrum
$p$
. We can therefore consider its formal spectrum
![]() $\operatorname{Spf}W(R)$
, and in this way, the theory of formal schemes can accommodate a satisfactory theory of Witt vector constructions of infinite length, as long as
$\operatorname{Spf}W(R)$
, and in this way, the theory of formal schemes can accommodate a satisfactory theory of Witt vector constructions of infinite length, as long as
![]() $R$
is perfect. For general rings
$R$
is perfect. For general rings
![]() $R$
, the inverse-limit topology on
$R$
, the inverse-limit topology on
![]() $W(R)$
is not an adic topology, and so the theory of formal schemes cannot even get started.
$W(R)$
is not an adic topology, and so the theory of formal schemes cannot even get started.
Another way of proceeding, also standard, is to view
![]() $\operatorname{Spec}W_{n}(R)$
as a sheaf of sets on the category of affine schemes, and to define
$\operatorname{Spec}W_{n}(R)$
as a sheaf of sets on the category of affine schemes, and to define
![]() $W(\operatorname{Spec}R)$
to be the direct limit
$W(\operatorname{Spec}R)$
to be the direct limit
![]() $\operatorname{colim}_{n}\operatorname{Spec}W_{n}(R)$
in this category. Since all limit and colimit constructions are as well behaved in categories of sheaves as they are in the category of sets, there is good reason to be confident in this approach. Indeed it works without problem and is the one we take.
$\operatorname{colim}_{n}\operatorname{Spec}W_{n}(R)$
in this category. Since all limit and colimit constructions are as well behaved in categories of sheaves as they are in the category of sets, there is good reason to be confident in this approach. Indeed it works without problem and is the one we take.
There is a second issue in defining
![]() $W(S)$
, which is how general we should allow
$W(S)$
, which is how general we should allow
![]() $S$
to be. It will be convenient later if we can allow
$S$
to be. It will be convenient later if we can allow
![]() $S$
to be the moduli space of ordinary elliptic curves (with sufficient level structure) over rings on which
$S$
to be the moduli space of ordinary elliptic curves (with sufficient level structure) over rings on which
![]() $p$
is nilpotent. But this does not exist in the category of schemes. It does exist in the category of formal schemes, where one can construct it as the ordinary locus in the
$p$
is nilpotent. But this does not exist in the category of schemes. It does exist in the category of formal schemes, where one can construct it as the ordinary locus in the
![]() $p$
-adic completion of the moduli space of all elliptic curves. However, it also exists in the category of sheaves mentioned above. Since we will be using this category anyway, it will be simpler to take that approach and forget about formal schemes entirely. It also has the side benefit of working for objects
$p$
-adic completion of the moduli space of all elliptic curves. However, it also exists in the category of sheaves mentioned above. Since we will be using this category anyway, it will be simpler to take that approach and forget about formal schemes entirely. It also has the side benefit of working for objects
![]() $S$
much more general than
$S$
much more general than
![]() $p$
-adic formal schemes.
$p$
-adic formal schemes.
2.1 Objects representable over sheaves
Let
![]() $\mathsf{Aff}$
denote the category of affine schemes, and let
$\mathsf{Aff}$
denote the category of affine schemes, and let
![]() $\mathsf{Aff}\sim$
denote the category of sheaves of sets on
$\mathsf{Aff}\sim$
denote the category of sheaves of sets on
![]() $\mathsf{Aff}$
with respect to the étale topology. (See SGA4 [Reference Artin, Grothendieck, Verdier, Bourbaki, Deligne and Saint-Donat2, exp. VII]) Any scheme
$\mathsf{Aff}$
with respect to the étale topology. (See SGA4 [Reference Artin, Grothendieck, Verdier, Bourbaki, Deligne and Saint-Donat2, exp. VII]) Any scheme
![]() $S$
can be viewed as an object of
$S$
can be viewed as an object of
![]() $\mathsf{Aff}\sim$
via the functor it represents
$\mathsf{Aff}\sim$
via the functor it represents
![]() $\operatorname{Spec}R\mapsto \text{Hom}(\operatorname{Spec}R,S)$
. This is a fully faithful embedding and we regard the category of schemes as a full subcategory of
$\operatorname{Spec}R\mapsto \text{Hom}(\operatorname{Spec}R,S)$
. This is a fully faithful embedding and we regard the category of schemes as a full subcategory of
![]() $\mathsf{Aff}\sim$
in this way without further comment.
$\mathsf{Aff}\sim$
in this way without further comment.
For any
![]() $S\in \mathsf{Aff}\sim$
, let
$S\in \mathsf{Aff}\sim$
, let
![]() $\mathsf{Aff}{\sim}_{S}$
denote the category of sheaves
$\mathsf{Aff}{\sim}_{S}$
denote the category of sheaves
![]() $X$
equipped with a map
$X$
equipped with a map
![]() $X\rightarrow S$
, where the morphisms are morphisms over
$X\rightarrow S$
, where the morphisms are morphisms over
![]() $S$
. If
$S$
. If
![]() $T\rightarrow S$
is a morphism, and
$T\rightarrow S$
is a morphism, and
![]() $X\in \mathsf{Aff}{\sim}_{S}$
, let
$X\in \mathsf{Aff}{\sim}_{S}$
, let
![]() $X_{T}$
denote the sheaf
$X_{T}$
denote the sheaf
![]() $T\times _{S}X$
together with the morphism
$T\times _{S}X$
together with the morphism
![]() $\text{pr}_{T}:T\times _{S}X\rightarrow T$
. We can then define familiar scheme-theoretic structures on objects
$\text{pr}_{T}:T\times _{S}X\rightarrow T$
. We can then define familiar scheme-theoretic structures on objects
![]() $X$
over
$X$
over
![]() $S$
by using affine test schemes. For example, an elliptic curve over
$S$
by using affine test schemes. For example, an elliptic curve over
![]() $S$
is a sheaf
$S$
is a sheaf
![]() $X$
over
$X$
over
![]() $S$
together with a compatible choice of an elliptic curve structure on
$S$
together with a compatible choice of an elliptic curve structure on
![]() $X_{T}$
for every morphism
$X_{T}$
for every morphism
![]() $T\rightarrow S$
from an affine scheme
$T\rightarrow S$
from an affine scheme
![]() $T$
. (To be clear, an elliptic curve structure on
$T$
. (To be clear, an elliptic curve structure on
![]() $X_{T}$
is by definition an isomorphism to
$X_{T}$
is by definition an isomorphism to
![]() $X_{T}$
from the sheaf represented by a usual elliptic curve over
$X_{T}$
from the sheaf represented by a usual elliptic curve over
![]() $T$
; and the compatibility condition is that for any morphism
$T$
; and the compatibility condition is that for any morphism
![]() $T^{\prime }\rightarrow T$
of affine schemes the isomorphism
$T^{\prime }\rightarrow T$
of affine schemes the isomorphism
![]() $(X_{T})_{T^{\prime }}\overset{{\sim}}{\rightarrow }X_{T^{\prime }}$
is a morphism of usual elliptic curves over
$(X_{T})_{T^{\prime }}\overset{{\sim}}{\rightarrow }X_{T^{\prime }}$
is a morphism of usual elliptic curves over
![]() $T^{\prime }$
.) Note that it also follows that the sheaf
$T^{\prime }$
.) Note that it also follows that the sheaf
![]() $X$
over
$X$
over
![]() $S$
admits a unique group structure (over
$S$
admits a unique group structure (over
![]() $S$
) inducing the group structures on the elliptic curves
$S$
) inducing the group structures on the elliptic curves
![]() $X_{T}$
over
$X_{T}$
over
![]() $T$
.
$T$
.
Descent theory for
![]() $\mathsf{Aff}\sim$
goes through for general sheaf-theoretic reasons. Suppose
$\mathsf{Aff}\sim$
goes through for general sheaf-theoretic reasons. Suppose
![]() $S^{\prime }\rightarrow S$
is an epimorphism in
$S^{\prime }\rightarrow S$
is an epimorphism in
![]() $\mathsf{Aff}\sim$
; in other words, every section of
$\mathsf{Aff}\sim$
; in other words, every section of
![]() $S$
lifts étale locally to one of
$S$
lifts étale locally to one of
![]() $S^{\prime }$
. Then any object of
$S^{\prime }$
. Then any object of
![]() $\mathsf{Aff}{\sim}_{S^{\prime }}$
equipped with descent data to
$\mathsf{Aff}{\sim}_{S^{\prime }}$
equipped with descent data to
![]() $S$
descends to a unique (up to unique isomorphism) object of
$S$
descends to a unique (up to unique isomorphism) object of
![]() $\mathsf{Aff}\sim$
over
$\mathsf{Aff}\sim$
over
![]() $S$
. This remains true if we are interested in objects
$S$
. This remains true if we are interested in objects
![]() $X$
with additional structure, as long as that structure is of an étale-local nature on affine schemes. This is the case for ordinary elliptic curves, as they satisfy effective descent for the étale topology, and is the only example we need.
$X$
with additional structure, as long as that structure is of an étale-local nature on affine schemes. This is the case for ordinary elliptic curves, as they satisfy effective descent for the étale topology, and is the only example we need.
There is a generalization of this which we also use. Suppose we are given a presentation of an object
![]() $S\in \mathsf{Aff}\sim$
as a colimit:
$S\in \mathsf{Aff}\sim$
as a colimit:
![]() $\operatorname{colim}_{i}S_{i}\overset{{\sim}}{\rightarrow }S$
. Then the category of objects over
$\operatorname{colim}_{i}S_{i}\overset{{\sim}}{\rightarrow }S$
. Then the category of objects over
![]() $\operatorname{colim}_{i}S_{i}$
is equivalent to the category of compatible families of objects over the
$\operatorname{colim}_{i}S_{i}$
is equivalent to the category of compatible families of objects over the
![]() $S_{i}$
. Indeed, an object
$S_{i}$
. Indeed, an object
![]() $X$
over
$X$
over
![]() $S$
gives rise to a compatible family of objects
$S$
gives rise to a compatible family of objects
![]() $X_{i}=S_{i}\times _{S}X$
over the
$X_{i}=S_{i}\times _{S}X$
over the
![]() $S_{i}$
, where compatible means that we are given morphisms
$S_{i}$
, where compatible means that we are given morphisms
![]() $X_{i}\rightarrow X_{j}$
lying over each morphism
$X_{i}\rightarrow X_{j}$
lying over each morphism
![]() $S_{i}\rightarrow S_{j}$
such that the induced maps
$S_{i}\rightarrow S_{j}$
such that the induced maps
![]() $X_{i}\rightarrow S_{i}\times _{S_{j}}X_{j}$
are isomorphisms. Conversely, to such a compatible family
$X_{i}\rightarrow S_{i}\times _{S_{j}}X_{j}$
are isomorphisms. Conversely, to such a compatible family
![]() $X_{i}$
we associate the object
$X_{i}$
we associate the object
![]() $X=\operatorname{colim}_{i}X_{i}$
. As above, the equivalence between objects over a colimit and compatible families also holds for objects with additional structure of an étale-local nature, such as ordinary elliptic curves. For general reasons, any sheaf
$X=\operatorname{colim}_{i}X_{i}$
. As above, the equivalence between objects over a colimit and compatible families also holds for objects with additional structure of an étale-local nature, such as ordinary elliptic curves. For general reasons, any sheaf
![]() $S$
admits such a presentation where each
$S$
admits such a presentation where each
![]() $S_{i}$
is an affine scheme, and so an ordinary elliptic curve (say) over
$S_{i}$
is an affine scheme, and so an ordinary elliptic curve (say) over
![]() $S$
is equivalent to a compatible family of ordinary elliptic curves over this diagram of affine schemes. More importantly, one often considers objects
$S$
is equivalent to a compatible family of ordinary elliptic curves over this diagram of affine schemes. More importantly, one often considers objects
![]() $S$
which are given as the colimit of some specific family of affine schemes, and then one can describe an elliptic curve over
$S$
which are given as the colimit of some specific family of affine schemes, and then one can describe an elliptic curve over
![]() $S$
as a compatible family of elliptic curves over this specific family. So an elliptic curve over an object given in these terms really is an accessible object.
$S$
as a compatible family of elliptic curves over this specific family. So an elliptic curve over an object given in these terms really is an accessible object.
2.2
 $p$
-adic sheaves
$p$
-adic sheaves
We say that a sheaf
![]() $S\in \mathsf{Aff}\sim$
is
$S\in \mathsf{Aff}\sim$
is
![]() $p$
-adic if it is isomorphic to a colimit
$p$
-adic if it is isomorphic to a colimit
![]() $\operatorname{colim}_{i}S_{i}$
of affine schemes
$\operatorname{colim}_{i}S_{i}$
of affine schemes
![]() $S_{i}$
on which
$S_{i}$
on which
![]() $p$
is nilpotent. (We require nothing of the indexing diagram of the colimit other than that it is small. In other language, this means that it is a set and not a proper class.) For example, a scheme is
$p$
is nilpotent. (We require nothing of the indexing diagram of the colimit other than that it is small. In other language, this means that it is a set and not a proper class.) For example, a scheme is
![]() $p$
-adic if and only if
$p$
-adic if and only if
![]() $p$
is locally nilpotent on it. In fact, any
$p$
is locally nilpotent on it. In fact, any
![]() $p$
-adic sheaf
$p$
-adic sheaf
![]() $S$
has the property that
$S$
has the property that
![]() $p$
is nilpotent on any affine scheme admitting a morphism to
$p$
is nilpotent on any affine scheme admitting a morphism to
![]() $S$
(and the converse is true up to issues of set-theoretic size just mentioned).
$S$
(and the converse is true up to issues of set-theoretic size just mentioned).
If
![]() $T$
is a scheme, put
$T$
is a scheme, put
Then we call
![]() $\widehat{T}=\operatorname{colim}_{n}T_{n}$
the
$\widehat{T}=\operatorname{colim}_{n}T_{n}$
the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $T$
. It is a
$T$
. It is a
![]() $p$
-adic sheaf because each
$p$
-adic sheaf because each
![]() $T_{n}$
is a scheme over
$T_{n}$
is a scheme over
![]() $\mathbb{Z}/p^{n+1}\mathbb{Z}$
and hence a colimit of affine schemes over
$\mathbb{Z}/p^{n+1}\mathbb{Z}$
and hence a colimit of affine schemes over
![]() $\mathbb{Z}/p^{n+1}\mathbb{Z}$
.
$\mathbb{Z}/p^{n+1}\mathbb{Z}$
.
We can do the same with any
![]() $p$
-adic formal scheme
$p$
-adic formal scheme
![]() $T$
, and this defines a fully faithful embedding of the category of
$T$
, and this defines a fully faithful embedding of the category of
![]() $p$
-adic formal schemes into the category of
$p$
-adic formal schemes into the category of
![]() $p$
-adic sheaves.
$p$
-adic sheaves.
3 Background on Witt vectors
3.1 Universal property of Witt vectors for rings
Let
![]() $A$
be a
$A$
be a
![]() $p$
-torsion-free ring with an endomorphism
$p$
-torsion-free ring with an endomorphism
![]() $\unicode[STIX]{x1D713}:A\rightarrow A$
such that
$\unicode[STIX]{x1D713}:A\rightarrow A$
such that
![]() $\unicode[STIX]{x1D713}(a)\equiv a^{p}\hspace{0.2em}{\rm mod}\hspace{0.2em}pA$
. Let
$\unicode[STIX]{x1D713}(a)\equiv a^{p}\hspace{0.2em}{\rm mod}\hspace{0.2em}pA$
. Let
![]() $R$
be any ring such that
$R$
be any ring such that
![]() $W(R)$
is
$W(R)$
is
![]() $p$
-torsion-free. (This does not hold in general, but it does hold at two opposite extremes—when
$p$
-torsion-free. (This does not hold in general, but it does hold at two opposite extremes—when
![]() $R$
is a perfect
$R$
is a perfect
![]() $\mathbb{F}_{p}$
-algebra and when
$\mathbb{F}_{p}$
-algebra and when
![]() $R$
is
$R$
is
![]() $p$
-torsion-free.) Then any ring map
$p$
-torsion-free.) Then any ring map
![]() $g:A\rightarrow R$
lifts to a unique ring map
$g:A\rightarrow R$
lifts to a unique ring map
![]() $\widetilde{g}$
$\widetilde{g}$
which is Frobenius equivariant, meaning that
![]() $F\circ \widetilde{g}=\widetilde{g}\circ \unicode[STIX]{x1D713}$
. In other words, the image of
$F\circ \widetilde{g}=\widetilde{g}\circ \unicode[STIX]{x1D713}$
. In other words, the image of
![]() $\widetilde{g}(a)$
under the ghost map
$\widetilde{g}(a)$
under the ghost map
![]() $W(R)\rightarrow R^{\mathbb{N}}$
is
$W(R)\rightarrow R^{\mathbb{N}}$
is
A proof using the traditional definition of Witt vectors can be found in Lazard’s book [Reference Lazard14, p. 215]. However, we remark that the traditional definition of Witt vectors will be irrelevant in this paper—it is only the universal property that matters. So a preferable alternative would be to take a definition of Witt vectors making the universal property obvious. For such a development, one can see Joyal [Reference Joyal10] for a concise account or [Reference Borger3, Section 1] for a more extensive one.
Observe that
![]() $\widetilde{g}:A\rightarrow W(R)$
agrees with the composition
$\widetilde{g}:A\rightarrow W(R)$
agrees with the composition
![]() $W(g)\circ \widetilde{\text{id}_{A}}:A\rightarrow W(A)\rightarrow W(R).$
We can therefore define a canonical map
$W(g)\circ \widetilde{\text{id}_{A}}:A\rightarrow W(A)\rightarrow W(R).$
We can therefore define a canonical map
![]() $\widetilde{g}$
without any restrictions on
$\widetilde{g}$
without any restrictions on
![]() $R$
. Indeed, we simply define
$R$
. Indeed, we simply define
![]() $\widetilde{g}=W(g)\circ \widetilde{\text{id}_{A}}$
. One might call
$\widetilde{g}=W(g)\circ \widetilde{\text{id}_{A}}$
. One might call
![]() $\widetilde{g}$
the canonical lift of
$\widetilde{g}$
the canonical lift of
![]() $g$
. We emphasize that while we have dropped all assumptions on
$g$
. We emphasize that while we have dropped all assumptions on
![]() $R$
here, we are still assuming
$R$
here, we are still assuming
![]() $A$
is
$A$
is
![]() $p$
-torsion-free. We also emphasize that while
$p$
-torsion-free. We also emphasize that while
![]() $\widetilde{g}$
is a canonically defined Frobenius equivariant lift of
$\widetilde{g}$
is a canonically defined Frobenius equivariant lift of
![]() $g$
, without any assumptions on
$g$
, without any assumptions on
![]() $R$
it might not be the unique one.
$R$
it might not be the unique one.
If we now write
![]() $Y=\operatorname{Spec}A$
, then for any ring
$Y=\operatorname{Spec}A$
, then for any ring
![]() $R$
, we have functorial maps
$R$
, we have functorial maps
![]() $Y(R)\rightarrow Y(W(R))$
given by
$Y(R)\rightarrow Y(W(R))$
given by
![]() $g\mapsto \widetilde{g}$
. In other words, if
$g\mapsto \widetilde{g}$
. In other words, if
![]() $Y$
is a
$Y$
is a
![]() $p$
-torsion-free moduli space parametrizing objects of some given type, a Frobenius lift on
$p$
-torsion-free moduli space parametrizing objects of some given type, a Frobenius lift on
![]() $Y$
defines a way of canonically lifting objects defined over
$Y$
defines a way of canonically lifting objects defined over
![]() $R$
to objects over
$R$
to objects over
![]() $W(R)$
. We might say that a class of objects has a theory of canonical lifts whenever their moduli space is
$W(R)$
. We might say that a class of objects has a theory of canonical lifts whenever their moduli space is
![]() $p$
-torsion-free and has a Frobenius lift. (For a little more along these lines see Section 7.4.) Indeed, this is the principle we apply below. But we need it in a slightly modified form because in our example, the Frobenius lift
$p$
-torsion-free and has a Frobenius lift. (For a little more along these lines see Section 7.4.) Indeed, this is the principle we apply below. But we need it in a slightly modified form because in our example, the Frobenius lift
![]() $\unicode[STIX]{x1D713}$
exists only on the
$\unicode[STIX]{x1D713}$
exists only on the
![]() $p$
-adic completion of the moduli space, which is not a scheme, but the
$p$
-adic completion of the moduli space, which is not a scheme, but the
![]() $p$
-adic completion of a scheme, in the sense of Section 2.2. The form of the universal property we need we be given in Section 3.3.
$p$
-adic completion of a scheme, in the sense of Section 2.2. The form of the universal property we need we be given in Section 3.3.
3.2 Witt vectors for schemes
Write
![]() $W_{n}:\mathsf{Aff}\rightarrow \mathsf{Aff}$
for the functor defined by
$W_{n}:\mathsf{Aff}\rightarrow \mathsf{Aff}$
for the functor defined by
![]() $W_{n}(\operatorname{Spec}R)=\operatorname{Spec}W_{n}(R)$
. The following theorem is fundamental:
$W_{n}(\operatorname{Spec}R)=\operatorname{Spec}W_{n}(R)$
. The following theorem is fundamental:
Theorem . The functor
![]() $W_{n}:\mathsf{Aff}\rightarrow \mathsf{Aff}$
preserves étale maps, étale covering families, and étale base change. In particular,
$W_{n}:\mathsf{Aff}\rightarrow \mathsf{Aff}$
preserves étale maps, étale covering families, and étale base change. In particular,
![]() $W_{n}$
is continuous in the étale topology.
$W_{n}$
is continuous in the étale topology.
The first general argument was given in van der Kallen [Reference van der Kallen17, (2.4)], but was written only for the ‘big’ Witt vector functor. For a proof for the
![]() $p$
-typical Witt vector functor considered here, one can see [Reference Borger3, Section 9.2]. One can also see the earlier paper by Langer and Zink [Reference Langer and Zink13, Appendix A]; note that while the results there are stated only under some finite-type assumptions, the general case can be deduced by a limiting argument. However, for all our applications, it is enough to consider Witt vectors of rings in which
$p$
-typical Witt vector functor considered here, one can see [Reference Borger3, Section 9.2]. One can also see the earlier paper by Langer and Zink [Reference Langer and Zink13, Appendix A]; note that while the results there are stated only under some finite-type assumptions, the general case can be deduced by a limiting argument. However, for all our applications, it is enough to consider Witt vectors of rings in which
![]() $p$
is nilpotent, and in this context the theorems in Langer–Zink do not have any finiteness assumptions and hence apply without modification.
$p$
is nilpotent, and in this context the theorems in Langer–Zink do not have any finiteness assumptions and hence apply without modification.
This allows us to extend
![]() $W_{n}$
to
$W_{n}$
to
![]() $\mathsf{Aff}\sim$
, by SGA4 [Reference Artin, Grothendieck, Verdier, Bourbaki, Deligne and Saint-Donat1, exp. III]. Indeed, because
$\mathsf{Aff}\sim$
, by SGA4 [Reference Artin, Grothendieck, Verdier, Bourbaki, Deligne and Saint-Donat1, exp. III]. Indeed, because
![]() $W_{n}$
is continuous, for any sheaf
$W_{n}$
is continuous, for any sheaf
![]() $S$
, the presheaf
$S$
, the presheaf
![]() $U\mapsto S(W_{n}(U))$
, for any
$U\mapsto S(W_{n}(U))$
, for any
![]() $U\in \mathsf{Aff}$
, is a sheaf. This defines a functor
$U\in \mathsf{Aff}$
, is a sheaf. This defines a functor
![]() $W_{n\ast }:\mathsf{Aff}\sim \rightarrow \mathsf{Aff}\sim$
, and it has a left adjoint
$W_{n\ast }:\mathsf{Aff}\sim \rightarrow \mathsf{Aff}\sim$
, and it has a left adjoint
![]() $W_{n}^{\ast }$
. Finally,
$W_{n}^{\ast }$
. Finally,
![]() $W_{n}^{\ast }$
extends
$W_{n}^{\ast }$
extends
![]() $W_{n}$
from
$W_{n}$
from
![]() $\mathsf{Aff}$
to
$\mathsf{Aff}$
to
![]() $\mathsf{Aff}\sim$
in the sense that we have canonical isomorphisms
$\mathsf{Aff}\sim$
in the sense that we have canonical isomorphisms
![]() $W_{n}^{\ast }(\operatorname{Spec}R)\overset{{\sim}}{\rightarrow }\operatorname{Spec}W_{n}(R)$
. So from now on, we often abusively write
$W_{n}^{\ast }(\operatorname{Spec}R)\overset{{\sim}}{\rightarrow }\operatorname{Spec}W_{n}(R)$
. So from now on, we often abusively write
![]() $W_{n}=W_{n}^{\ast }$
.
$W_{n}=W_{n}^{\ast }$
.
Since
![]() $W_{n}:\mathsf{Aff}\sim \rightarrow \mathsf{Aff}\sim$
is a left adjoint, it preserves colimits. Therefore, any presentation
$W_{n}:\mathsf{Aff}\sim \rightarrow \mathsf{Aff}\sim$
is a left adjoint, it preserves colimits. Therefore, any presentation
![]() $f:\operatorname{colim}_{i}\operatorname{Spec}R_{i}\overset{{\sim}}{\rightarrow }S$
gives rise to a presentation
$f:\operatorname{colim}_{i}\operatorname{Spec}R_{i}\overset{{\sim}}{\rightarrow }S$
gives rise to a presentation
Therefore, by the remarks in Section 2.1, an elliptic curve over
![]() $W_{n}(S)$
can be understood as a compatible system of elliptic curves over the
$W_{n}(S)$
can be understood as a compatible system of elliptic curves over the
![]() $W_{n}(S_{i})$
, and similarly for any other kind of object having a local nature.
$W_{n}(S_{i})$
, and similarly for any other kind of object having a local nature.
Observe that if
![]() $S$
is a
$S$
is a
![]() $p$
-adic sheaf, then so is
$p$
-adic sheaf, then so is
![]() $W_{n}(S)$
. Indeed, it is sufficient (and necessary) to observe that if
$W_{n}(S)$
. Indeed, it is sufficient (and necessary) to observe that if
![]() $p$
is nilpotent in a ring
$p$
is nilpotent in a ring
![]() $R$
, then it is nilpotent in
$R$
, then it is nilpotent in
![]() $W_{n}(R)$
. One way to show this is to observe that the comonad structure map
$W_{n}(R)$
. One way to show this is to observe that the comonad structure map
![]() $W_{m+n}(\mathbb{F}_{p})\rightarrow W_{n}(W_{m}(\mathbb{F}_{p}))$
makes
$W_{m+n}(\mathbb{F}_{p})\rightarrow W_{n}(W_{m}(\mathbb{F}_{p}))$
makes
![]() $W_{n}(\mathbb{Z}/p^{m+1}\mathbb{Z})$
into a
$W_{n}(\mathbb{Z}/p^{m+1}\mathbb{Z})$
into a
![]() $\mathbb{Z}/p^{m+n+1}\mathbb{Z}$
-algebra.
$\mathbb{Z}/p^{m+n+1}\mathbb{Z}$
-algebra.
In fact, if
![]() $S$
is a scheme on which
$S$
is a scheme on which
![]() $p$
is locally nilpotent, then so is
$p$
is locally nilpotent, then so is
![]() $W_{n}(S)$
. We will not use this below and mention it only for the reader who is more comfortable with schemes than abstract sheaf theory. As a topological space,
$W_{n}(S)$
. We will not use this below and mention it only for the reader who is more comfortable with schemes than abstract sheaf theory. As a topological space,
![]() $W_{n}(S)$
agrees with
$W_{n}(S)$
agrees with
![]() $S$
, and its structure sheaf
$S$
, and its structure sheaf
![]() ${\mathcal{O}}_{W_{n}(S)}$
is given by the presheaf
${\mathcal{O}}_{W_{n}(S)}$
is given by the presheaf
![]() $U\mapsto W_{n}({\mathcal{O}}_{S}(U))$
. One way to show this is by using the fact that for any ring
$U\mapsto W_{n}({\mathcal{O}}_{S}(U))$
. One way to show this is by using the fact that for any ring
![]() $R$
and any element
$R$
and any element
![]() $f\in R$
, we have
$f\in R$
, we have
![]() $W_{n}(R[1/f])=W_{n}(R)[1/[f]]$
, where
$W_{n}(R[1/f])=W_{n}(R)[1/[f]]$
, where
![]() $[f]$
denotes the Teichmüller lift of
$[f]$
denotes the Teichmüller lift of
![]() $f$
. Alternatively, open immersions are the same as étale monomorphisms and hence are preserved by
$f$
. Alternatively, open immersions are the same as étale monomorphisms and hence are preserved by
![]() $W_{n}$
, by the theorem above.
$W_{n}$
, by the theorem above.
Then we define
We emphasize that this colimit is taken in
![]() $\mathsf{Aff}\sim$
. Thus
$\mathsf{Aff}\sim$
. Thus
![]() $W$
is the left adjoint of
$W$
is the left adjoint of
![]() $\lim _{n}W_{n\ast }$
. If
$\lim _{n}W_{n\ast }$
. If
![]() $S=\operatorname{colim}_{i}S_{i}$
, then we have
$S=\operatorname{colim}_{i}S_{i}$
, then we have
![]() $W(S)=\operatorname{colim}_{n,i}W_{n}(S_{i})$
. Therefore, if
$W(S)=\operatorname{colim}_{n,i}W_{n}(S_{i})$
. Therefore, if
![]() $S$
is a
$S$
is a
![]() $p$
-adic sheaf, then so is
$p$
-adic sheaf, then so is
![]() $W(S)$
. But
$W(S)$
. But
![]() $W(S)$
is typically not a scheme, even if
$W(S)$
is typically not a scheme, even if
![]() $S$
is. (For instance, if
$S$
is. (For instance, if
![]() $S=\operatorname{Spec}\mathbb{F}_{p}$
, then
$S=\operatorname{Spec}\mathbb{F}_{p}$
, then
![]() $W(S)$
is the colimit of
$W(S)$
is the colimit of
![]() $\operatorname{Spec}\mathbb{Z}/p^{n+1}\mathbb{Z}$
, which represents the functor sending
$\operatorname{Spec}\mathbb{Z}/p^{n+1}\mathbb{Z}$
, which represents the functor sending
![]() $\operatorname{Spec}R$
to the one-point set if
$\operatorname{Spec}R$
to the one-point set if
![]() $p$
is nilpotent in
$p$
is nilpotent in
![]() $R$
and to the empty set otherwise. This is representable by the formal scheme
$R$
and to the empty set otherwise. This is representable by the formal scheme
![]() $\operatorname{Spf}\mathbb{Z}_{p}$
but not by a scheme.) It is, however, still easy to work with. For example, if
$\operatorname{Spf}\mathbb{Z}_{p}$
but not by a scheme.) It is, however, still easy to work with. For example, if
![]() $T$
is an affine scheme, then the set
$T$
is an affine scheme, then the set
![]() $\text{Hom}(T,W(S))$
is the filtered colimit
$\text{Hom}(T,W(S))$
is the filtered colimit
![]() $\operatorname{colim}_{n}\text{Hom}(T,W_{n}(S))$
. (By for example SGA4 [Reference Artin, Grothendieck, Verdier, Bourbaki, Deligne and Saint-Donat2, exp. VI, Theorem 1.23(ii) on p. 185]) So if
$\operatorname{colim}_{n}\text{Hom}(T,W_{n}(S))$
. (By for example SGA4 [Reference Artin, Grothendieck, Verdier, Bourbaki, Deligne and Saint-Donat2, exp. VI, Theorem 1.23(ii) on p. 185]) So if
![]() $S$
is a scheme, for example, then any map
$S$
is a scheme, for example, then any map
![]() $T\rightarrow W(S)$
factors through the scheme
$T\rightarrow W(S)$
factors through the scheme
![]() $W_{n}(S)$
for some
$W_{n}(S)$
for some
![]() $n$
.
$n$
.
Note that
![]() $W_{n}$
and
$W_{n}$
and
![]() $W$
preserve epimorphisms in
$W$
preserve epimorphisms in
![]() $\mathsf{Aff}\sim$
, as they are left adjoints. In particular, if
$\mathsf{Aff}\sim$
, as they are left adjoints. In particular, if
![]() $S^{\prime }\rightarrow S$
is an étale cover of schemes, then
$S^{\prime }\rightarrow S$
is an étale cover of schemes, then
![]() $W(S^{\prime })\rightarrow W(S)$
is an epimorphism, and hence descent is available.
$W(S^{\prime })\rightarrow W(S)$
is an epimorphism, and hence descent is available.
3.3 The universal property of Witt vectors for
 $p$
-adic sheaves
$p$
-adic sheaves
Let
![]() $A$
be a
$A$
be a
![]() $p$
-torsion-free ring with a Frobenius lift
$p$
-torsion-free ring with a Frobenius lift
![]() $\unicode[STIX]{x1D713}$
. Let
$\unicode[STIX]{x1D713}$
. Let
![]() $Y_{m}=\operatorname{Spec}A/p^{m+1}A$
,
$Y_{m}=\operatorname{Spec}A/p^{m+1}A$
,
![]() $\widehat{Y}=\operatorname{colim}_{m}Y_{m}$
, as in Section 2.2, and
$\widehat{Y}=\operatorname{colim}_{m}Y_{m}$
, as in Section 2.2, and
![]() $\widehat{\unicode[STIX]{x1D713}}:\widehat{Y}\rightarrow \widehat{Y}$
be the Frobenius lift induced by
$\widehat{\unicode[STIX]{x1D713}}:\widehat{Y}\rightarrow \widehat{Y}$
be the Frobenius lift induced by
![]() $\unicode[STIX]{x1D713}$
. Let
$\unicode[STIX]{x1D713}$
. Let
![]() $S$
be a
$S$
be a
![]() $p$
-adic sheaf and let
$p$
-adic sheaf and let
![]() $f:S\rightarrow \widehat{Y}$
be a morphism. Write
$f:S\rightarrow \widehat{Y}$
be a morphism. Write
![]() $S=\operatorname{colim}_{i}\operatorname{Spec}R_{i}$
, with
$S=\operatorname{colim}_{i}\operatorname{Spec}R_{i}$
, with
![]() $p$
nilpotent in each ring
$p$
nilpotent in each ring
![]() $R_{i}$
. Then for each
$R_{i}$
. Then for each
![]() $i$
, there exists an
$i$
, there exists an
![]() $m_{i}$
such that the map
$m_{i}$
such that the map
![]() $\operatorname{Spec}R_{i}\rightarrow \widehat{Y}$
factors through the inclusion
$\operatorname{Spec}R_{i}\rightarrow \widehat{Y}$
factors through the inclusion
![]() $Y_{m_{i}}\rightarrow \widehat{Y}$
, thus inducing a map
$Y_{m_{i}}\rightarrow \widehat{Y}$
, thus inducing a map
![]() $A/p^{m_{i}+1}A\rightarrow R_{i}$
. Let
$A/p^{m_{i}+1}A\rightarrow R_{i}$
. Let
![]() $g$
denote the composition
$g$
denote the composition
![]() $A\rightarrow A/p^{m_{i}+1}A\rightarrow R_{i}$
, and let
$A\rightarrow A/p^{m_{i}+1}A\rightarrow R_{i}$
, and let
![]() $\widetilde{g}$
denote the canonical lift as defined in 3.1. Then for each
$\widetilde{g}$
denote the canonical lift as defined in 3.1. Then for each
![]() $n$
, the composition
$n$
, the composition
factors through
![]() $A\rightarrow A/p^{N_{i,n}+1}A$
for some
$A\rightarrow A/p^{N_{i,n}+1}A$
for some
![]() $N_{i,n}$
(in fact, for any
$N_{i,n}$
(in fact, for any
![]() $N_{i,n}\geqslant m_{i}+n$
). This defines a compatible family of maps
$N_{i,n}\geqslant m_{i}+n$
). This defines a compatible family of maps
and hence, by the universal property of colimits, a map
which we again call the canonical lift of
![]() $f:S\rightarrow \widehat{Y}$
. Note that as with the previously defined canonical lift maps, the map
$f:S\rightarrow \widehat{Y}$
. Note that as with the previously defined canonical lift maps, the map
![]() $\widetilde{f}$
is Frobenius equivariant, which is to say
$\widetilde{f}$
is Frobenius equivariant, which is to say
![]() $\widetilde{f}\circ \widehat{\unicode[STIX]{x1D713}}=F\circ \widetilde{f}$
.
$\widetilde{f}\circ \widehat{\unicode[STIX]{x1D713}}=F\circ \widetilde{f}$
.
4 Statement of the theorem
We return to the notation of the introduction, where
![]() $R$
is a ring in which
$R$
is a ring in which
![]() $p$
is nilpotent and
$p$
is nilpotent and
![]() $S=\operatorname{Spec}R$
. Then the usual Witt vector Frobenius map
$S=\operatorname{Spec}R$
. Then the usual Witt vector Frobenius map
![]() $F:W_{n+1}(R)\rightarrow W_{n}(R)$
induces functorial maps
$F:W_{n+1}(R)\rightarrow W_{n}(R)$
induces functorial maps
![]() $F:W_{n}(S)\rightarrow W_{n+1}(S)$
, for any
$F:W_{n}(S)\rightarrow W_{n+1}(S)$
, for any
![]() $S\in \mathsf{Aff}\sim$
, and upon taking colimits, maps
$S\in \mathsf{Aff}\sim$
, and upon taking colimits, maps
![]() $F:W(S)\rightarrow W(S)$
. It also satisfies the relation
$F:W(S)\rightarrow W(S)$
. It also satisfies the relation
![]() $F(x)\equiv r(x)^{p}\hspace{0.2em}{\rm mod}\hspace{0.2em}pW_{n}(R)$
, where
$F(x)\equiv r(x)^{p}\hspace{0.2em}{\rm mod}\hspace{0.2em}pW_{n}(R)$
, where
![]() $r:W_{n+1}(R)\rightarrow W_{n}(R)$
denotes the usual projection. So the maps
$r:W_{n+1}(R)\rightarrow W_{n}(R)$
denotes the usual projection. So the maps
![]() $F:W(S)\rightarrow W(S)$
agree with the usual
$F:W(S)\rightarrow W(S)$
agree with the usual
![]() $p$
th power Frobenius map on the locus
$p$
th power Frobenius map on the locus
![]() $\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W(S)$
.
$\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W(S)$
.
Let us then say that a Frobenius lift on an elliptic curve
![]() $E$
over
$E$
over
![]() $W(S)$
is a morphism
$W(S)$
is a morphism
![]() $E\rightarrow F^{\ast }(E)$
of elliptic curves over
$E\rightarrow F^{\ast }(E)$
of elliptic curves over
![]() $W(S)$
restricting to the usual Frobenius map on
$W(S)$
restricting to the usual Frobenius map on
![]() $\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W(S)$
.
$\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W(S)$
.
Theorem . There is a unique way of lifting ordinary elliptic curves
![]() $E$
over
$E$
over
![]() $p$
-adic sheaves
$p$
-adic sheaves
![]() $S$
to elliptic curves
$S$
to elliptic curves
![]() $\widetilde{E}$
over
$\widetilde{E}$
over
![]() $W(S)$
such that the construction
$W(S)$
such that the construction
![]() $E\mapsto \widetilde{E}$
is compatible with base change in
$E\mapsto \widetilde{E}$
is compatible with base change in
![]() $S$
and such that each
$S$
and such that each
![]() $\widetilde{E}$
admits a Frobenius lift.
$\widetilde{E}$
admits a Frobenius lift.
We make some remarks to clarify the statement. First, the base-change condition, which can be written
![]() $(E_{S^{\prime }})^{{\sim}}=\widetilde{E}_{W(S^{\prime })}$
for any map
$(E_{S^{\prime }})^{{\sim}}=\widetilde{E}_{W(S^{\prime })}$
for any map
![]() $S^{\prime }\rightarrow S$
, is more properly expressed as a coherent family of isomorphisms. Second, the uniqueness statement is to be understood as follows: if
$S^{\prime }\rightarrow S$
, is more properly expressed as a coherent family of isomorphisms. Second, the uniqueness statement is to be understood as follows: if
![]() $E\mapsto \check{E}$
is any other such construction, then there is a unique family of isomorphisms
$E\mapsto \check{E}$
is any other such construction, then there is a unique family of isomorphisms
![]() $\widetilde{E}\rightarrow \check{E}$
, where
$\widetilde{E}\rightarrow \check{E}$
, where
![]() $E$
runs over all ordinary elliptic curves
$E$
runs over all ordinary elliptic curves
![]() $E$
over all
$E$
over all
![]() $p$
-adic base sheaves
$p$
-adic base sheaves
![]() $S$
, which are Frobenius equivariant and compatible with restriction of the base
$S$
, which are Frobenius equivariant and compatible with restriction of the base
![]() $S$
. We emphasize that such a uniqueness statement does not apply to lifts of a single elliptic curve or even all elliptic curves over a given base
$S$
. We emphasize that such a uniqueness statement does not apply to lifts of a single elliptic curve or even all elliptic curves over a given base
![]() $S$
but only to the family of all elliptic curves over all bases. However, see Theorem 6.1 for a result in this direction.
$S$
but only to the family of all elliptic curves over all bases. However, see Theorem 6.1 for a result in this direction.
5 Existence
In this section, we construct the canonical lift functor. In the presence of enough level structure, it is nothing more than the universal property of Witt vectors applied to the moduli space of ordinary elliptic curves with its canonical Frobenius lift. In general, we use a descent argument to pass from the case with level structure to the general setting.
5.1 Existence with level structure
Let
![]() $Y(N)$
denote the moduli space of elliptic curves
$Y(N)$
denote the moduli space of elliptic curves
![]() $E/S$
with full level-
$E/S$
with full level-
![]() $N$
structure
$N$
structure
![]() $\unicode[STIX]{x1D709}:(\mathbb{Z}/N\mathbb{Z})^{2}\overset{{\sim}}{\rightarrow }E[N](S)$
. We assume
$\unicode[STIX]{x1D709}:(\mathbb{Z}/N\mathbb{Z})^{2}\overset{{\sim}}{\rightarrow }E[N](S)$
. We assume
![]() $p\nmid N$
and that
$p\nmid N$
and that
![]() $N$
is large enough to make the moduli problem representable. (So
$N$
is large enough to make the moduli problem representable. (So
![]() $N\geqslant 3$
is enough.) In this case,
$N\geqslant 3$
is enough.) In this case,
![]() $Y(N)$
is a smooth affine scheme of relative dimension one over
$Y(N)$
is a smooth affine scheme of relative dimension one over
![]() $\operatorname{Spec}\mathbb{Z}[1/N]$
. Let
$\operatorname{Spec}\mathbb{Z}[1/N]$
. Let
![]() $T$
denote the open subscheme of
$T$
denote the open subscheme of
![]() $Y(N)$
which is the complement of the supersingular locus on the fiber over
$Y(N)$
which is the complement of the supersingular locus on the fiber over
![]() $p$
, and let
$p$
, and let
![]() $Y(N)^{\text{o}}$
denote its
$Y(N)^{\text{o}}$
denote its
![]() $p$
-adic completion
$p$
-adic completion
![]() $\widehat{T}$
, in the sense of Section 2.2. Then
$\widehat{T}$
, in the sense of Section 2.2. Then
![]() $Y(N)^{\text{o}}$
has the form
$Y(N)^{\text{o}}$
has the form
![]() $\operatorname{colim}_{n}\operatorname{Spec}A_{N}/p^{n+1}A_{N}$
, where
$\operatorname{colim}_{n}\operatorname{Spec}A_{N}/p^{n+1}A_{N}$
, where
![]() $A_{N}$
is
$A_{N}$
is
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion-free. Indeed, if we write
$p$
-torsion-free. Indeed, if we write
![]() $Y(N)=\operatorname{Spec}R$
, then
$Y(N)=\operatorname{Spec}R$
, then
![]() $A_{N}$
is the
$A_{N}$
is the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $R[Q^{-1}]$
, for any subset
$R[Q^{-1}]$
, for any subset
![]() $Q\subset R$
such that
$Q\subset R$
such that
![]() $\operatorname{Spec}R[Q^{-1}]/(p)$
is the ordinary locus of the fiber of
$\operatorname{Spec}R[Q^{-1}]/(p)$
is the ordinary locus of the fiber of
![]() $Y(N)$
over
$Y(N)$
over
![]() $p$
. It follows that
$p$
. It follows that
![]() $A_{N}$
is
$A_{N}$
is
![]() $p$
-torsion-free because
$p$
-torsion-free because
![]() $R$
smooth over
$R$
smooth over
![]() $\mathbb{Z}[1/N]$
and hence
$\mathbb{Z}[1/N]$
and hence
![]() $p$
-torsion-free. Therefore, it has the form needed to apply the universal property of Section 3.3.
$p$
-torsion-free. Therefore, it has the form needed to apply the universal property of Section 3.3.
Recall the standard Frobenius lift
![]() $\unicode[STIX]{x1D713}$
on
$\unicode[STIX]{x1D713}$
on
![]() $Y(N)^{\text{o}}$
. Let
$Y(N)^{\text{o}}$
. Let
![]() $E$
be an ordinary elliptic curve over an affine scheme
$E$
be an ordinary elliptic curve over an affine scheme
![]() $S$
on which
$S$
on which
![]() $p$
is nilpotent, and let
$p$
is nilpotent, and let
![]() $E^{\text{can}}$
denote its canonical subgroup, the connected component of its
$E^{\text{can}}$
denote its canonical subgroup, the connected component of its
![]() $p$
-torsion subgroup-scheme [Reference Katz11, Chapter 3]. It is a finite flat closed subgroup-scheme of
$p$
-torsion subgroup-scheme [Reference Katz11, Chapter 3]. It is a finite flat closed subgroup-scheme of
![]() $E$
. Let
$E$
. Let
![]() $E/E^{\text{can}}$
denote the usual quotient (so not the quotient object in
$E/E^{\text{can}}$
denote the usual quotient (so not the quotient object in
![]() $\mathsf{Aff}\sim$
, but the quotient with respect to the fppf topology). Thus
$\mathsf{Aff}\sim$
, but the quotient with respect to the fppf topology). Thus
![]() $E/E^{\text{can}}$
is also a family of ordinary elliptic curves over
$E/E^{\text{can}}$
is also a family of ordinary elliptic curves over
![]() $S$
, and the quotient map
$S$
, and the quotient map
![]() $E\rightarrow E/E^{\text{can}}$
is faithfully flat. Further, if
$E\rightarrow E/E^{\text{can}}$
is faithfully flat. Further, if
![]() $\unicode[STIX]{x1D709}$
is a level-
$\unicode[STIX]{x1D709}$
is a level-
![]() $N$
structure on
$N$
structure on
![]() $E$
, then its image
$E$
, then its image
![]() $\bar{\unicode[STIX]{x1D709}}$
in
$\bar{\unicode[STIX]{x1D709}}$
in
![]() $E/E^{\text{can}}$
is still a level-
$E/E^{\text{can}}$
is still a level-
![]() $N$
structure. We then let
$N$
structure. We then let
![]() $\unicode[STIX]{x1D713}$
denote the map
$\unicode[STIX]{x1D713}$
denote the map
![]() $Y(N)^{\text{o}}\rightarrow Y(N)^{\text{o}}$
that, for any
$Y(N)^{\text{o}}\rightarrow Y(N)^{\text{o}}$
that, for any
![]() $S$
, sends an
$S$
, sends an
![]() $S$
-valued point
$S$
-valued point
![]() $(E,\unicode[STIX]{x1D709})$
to
$(E,\unicode[STIX]{x1D709})$
to
![]() $(E/E^{\text{can}},\bar{\unicode[STIX]{x1D709}})$
. It is a Frobenius lift because for ordinary elliptic curves over
$(E/E^{\text{can}},\bar{\unicode[STIX]{x1D709}})$
. It is a Frobenius lift because for ordinary elliptic curves over
![]() $\mathbb{F}_{p}$
-algebras, the connected component of the
$\mathbb{F}_{p}$
-algebras, the connected component of the
![]() $p$
-torsion subgroup-scheme agrees with the kernel of Frobenius.
$p$
-torsion subgroup-scheme agrees with the kernel of Frobenius.
Now let
![]() $(E,\unicode[STIX]{x1D709})$
be an ordinary elliptic curve with level-
$(E,\unicode[STIX]{x1D709})$
be an ordinary elliptic curve with level-
![]() $N$
structure over a
$N$
structure over a
![]() $p$
-adic sheaf
$p$
-adic sheaf
![]() $S$
. This is the pull-back of the universal object
$S$
. This is the pull-back of the universal object
![]() $(\mathscr{E},\unicode[STIX]{x1D709}^{\text{u}})$
through a unique map
$(\mathscr{E},\unicode[STIX]{x1D709}^{\text{u}})$
through a unique map
![]() $c:S\rightarrow Y(N)^{\text{o}}$
. Since the ring
$c:S\rightarrow Y(N)^{\text{o}}$
. Since the ring
![]() $A_{N}$
is
$A_{N}$
is
![]() $p$
-torsion-free, we can apply the universal property of Witt vectors as given in Section 3.3 and write
$p$
-torsion-free, we can apply the universal property of Witt vectors as given in Section 3.3 and write
for the morphism induced by
![]() $c$
. We then let
$c$
. We then let
![]() $(E,\unicode[STIX]{x1D709})^{{\sim}}$
denote the canonical lift of
$(E,\unicode[STIX]{x1D709})^{{\sim}}$
denote the canonical lift of
![]() $(E,\unicode[STIX]{x1D709})$
, which is to say the pull-back
$(E,\unicode[STIX]{x1D709})$
, which is to say the pull-back
![]() $\widetilde{c}^{\ast }((\mathscr{E},\unicode[STIX]{x1D709}^{\text{u}}))$
of the universal elliptic curve with level-
$\widetilde{c}^{\ast }((\mathscr{E},\unicode[STIX]{x1D709}^{\text{u}}))$
of the universal elliptic curve with level-
![]() $N$
structure. The assignment
$N$
structure. The assignment
now defines our theory of canonical lifts for elliptic curves with full level-
![]() $N$
structure. We could write
$N$
structure. We could write
![]() $(E,\unicode[STIX]{x1D709})^{{\sim}}=(\widetilde{E},\widetilde{\unicode[STIX]{x1D709}})$
, but it will not be until the next section that we know
$(E,\unicode[STIX]{x1D709})^{{\sim}}=(\widetilde{E},\widetilde{\unicode[STIX]{x1D709}})$
, but it will not be until the next section that we know
![]() $\widetilde{E}$
is canonically independent of the choice of
$\widetilde{E}$
is canonically independent of the choice of
![]() $\unicode[STIX]{x1D709}$
.
$\unicode[STIX]{x1D709}$
.
5.2 Existence in general
We use a standard descent argument. So let
![]() $Y(N,N)$
denote the moduli space of elliptic curves with a pair of full level-
$Y(N,N)$
denote the moduli space of elliptic curves with a pair of full level-
![]() $N$
structures
$N$
structures
![]() $(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$
. Forgetting one or the other defines projections
$(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$
. Forgetting one or the other defines projections
![]() $Y(N,N)\rightrightarrows Y(N)$
, both which are finite étale. Now we proceed as we did with
$Y(N,N)\rightrightarrows Y(N)$
, both which are finite étale. Now we proceed as we did with
![]() $Y(N)^{\text{o}}$
. Let
$Y(N)^{\text{o}}$
. Let
![]() $Y(N,N)^{\text{o}}$
denote the
$Y(N,N)^{\text{o}}$
denote the
![]() $p$
-adic completion of the complement of the supersingular locus on the fiber over
$p$
-adic completion of the complement of the supersingular locus on the fiber over
![]() $p$
. Then
$p$
. Then
![]() $Y(N,N)^{\text{o}}$
is of the form
$Y(N,N)^{\text{o}}$
is of the form
![]() $\operatorname{colim}_{n}\operatorname{Spec}A_{N,N}/p^{n+1}A_{N,N}$
, where
$\operatorname{colim}_{n}\operatorname{Spec}A_{N,N}/p^{n+1}A_{N,N}$
, where
![]() $A_{N,N}$
is a
$A_{N,N}$
is a
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion-free ring, and it has a Frobenius lift, also denoted
$p$
-torsion-free ring, and it has a Frobenius lift, also denoted
![]() $\unicode[STIX]{x1D713}$
, defined by sending an elliptic curve to its quotient by the canonical subgroup, with the image level structures. This defines a theory of canonical lifts for elliptic curves with pairs of full level-
$\unicode[STIX]{x1D713}$
, defined by sending an elliptic curve to its quotient by the canonical subgroup, with the image level structures. This defines a theory of canonical lifts for elliptic curves with pairs of full level-
![]() $N$
structure. It is compatible with the projections
$N$
structure. It is compatible with the projections
![]() $Y(N,N)\rightrightarrows Y(N)$
in the sense that taking the canonical lift commutes with forgetting each of the level structures. This is simply because the Frobenius lift
$Y(N,N)\rightrightarrows Y(N)$
in the sense that taking the canonical lift commutes with forgetting each of the level structures. This is simply because the Frobenius lift
![]() $\unicode[STIX]{x1D713}$
commutes with the projections.
$\unicode[STIX]{x1D713}$
commutes with the projections.
We can now define the canonical lift of an arbitrary ordinary elliptic curve
![]() $E$
over a
$E$
over a
![]() $p$
-adic sheaf
$p$
-adic sheaf
![]() $S$
. It will in fact be enough to do this for affine schemes
$S$
. It will in fact be enough to do this for affine schemes
![]() $S$
, as the construction will be compatible with base change along morphisms of affine schemes, so that if
$S$
, as the construction will be compatible with base change along morphisms of affine schemes, so that if
![]() $S$
is an arbitrary
$S$
is an arbitrary
![]() $p$
-adic sheaf and
$p$
-adic sheaf and
![]() $E$
is an ordinary elliptic curve over
$E$
is an ordinary elliptic curve over
![]() $S$
, writing
$S$
, writing
![]() $S=\operatorname{colim}_{i}S_{i}$
as a colimit of affine schemes, we may define
$S=\operatorname{colim}_{i}S_{i}$
as a colimit of affine schemes, we may define
![]() $\widetilde{E}$
over
$\widetilde{E}$
over
![]() $W(S)$
to be
$W(S)$
to be
![]() $\operatorname{colim}_{i}(E_{S_{i}})^{{\sim}}$
over
$\operatorname{colim}_{i}(E_{S_{i}})^{{\sim}}$
over
![]() $W(S)=\operatorname{colim}_{i}W(S_{i})$
, as in Section 2.1.
$W(S)=\operatorname{colim}_{i}W(S_{i})$
, as in Section 2.1.
So let
![]() $E$
be an ordinary elliptic curve over an affine
$E$
be an ordinary elliptic curve over an affine
![]() $p$
-adic scheme
$p$
-adic scheme
![]() $S$
. Let
$S$
. Let
![]() $S^{\prime }$
be the universal cover of
$S^{\prime }$
be the universal cover of
![]() $S$
over which
$S$
over which
![]() $E$
admits a level-
$E$
admits a level-
![]() $N$
structure
$N$
structure
![]() $\unicode[STIX]{x1D709}$
. The covering morphism
$\unicode[STIX]{x1D709}$
. The covering morphism
![]() $S^{\prime }\rightarrow S$
is then finite and étale, and we have a diagram
$S^{\prime }\rightarrow S$
is then finite and étale, and we have a diagram

Each column has the structure of a groupoid object in the category
![]() $\mathsf{Aff}\sim$
in which the displayed projections are the source and target structure maps. Indeed,
$\mathsf{Aff}\sim$
in which the displayed projections are the source and target structure maps. Indeed,
![]() $S^{\prime }\times _{S}S^{\prime }$
is an equivalence-relation object on
$S^{\prime }\times _{S}S^{\prime }$
is an equivalence-relation object on
![]() $S^{\prime }$
over
$S^{\prime }$
over
![]() $S$
, and hence it admits a unique groupoid structure over
$S$
, and hence it admits a unique groupoid structure over
![]() $S$
. On the right column, the groupoid structure
$S$
. On the right column, the groupoid structure
![]() $Y(N,N)^{\text{o}}$
over
$Y(N,N)^{\text{o}}$
over
![]() $Y(N)^{\text{o}}$
is the one with composition given by
$Y(N)^{\text{o}}$
is the one with composition given by
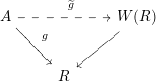
whenever there is an isomorphism
![]() $\unicode[STIX]{x1D6FD}:(E,\unicode[STIX]{x1D709}_{2})\overset{{\sim}}{\rightarrow }(E^{\prime },\unicode[STIX]{x1D709}_{1}^{\prime })$
, which is unique when it exists. With respect to these groupoid structures, this diagram becomes a morphism of groupoid objects. Because the right column has Frobenius lifts which are compatible with the projections, the universal property of Witt vectors then gives us a diagram
$\unicode[STIX]{x1D6FD}:(E,\unicode[STIX]{x1D709}_{2})\overset{{\sim}}{\rightarrow }(E^{\prime },\unicode[STIX]{x1D709}_{1}^{\prime })$
, which is unique when it exists. With respect to these groupoid structures, this diagram becomes a morphism of groupoid objects. Because the right column has Frobenius lifts which are compatible with the projections, the universal property of Witt vectors then gives us a diagram
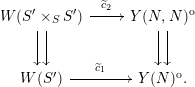
By the theorem in Section 3.2, we have
and so the diagram above can be identified with
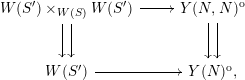
which is easily seen to be a morphism of groupoid objects again. In other words, there is a family over
![]() $W(S^{\prime })$
equipped with descent data to
$W(S^{\prime })$
equipped with descent data to
![]() $W(S)$
. Since
$W(S)$
. Since
![]() $W$
preserves epimorphisms, as explained above, the map
$W$
preserves epimorphisms, as explained above, the map
![]() $W(S^{\prime })\rightarrow W(S)$
is an effective descent morphism for elliptic curves. So we can define
$W(S^{\prime })\rightarrow W(S)$
is an effective descent morphism for elliptic curves. So we can define
![]() $\widetilde{E}$
to be the descended object over
$\widetilde{E}$
to be the descended object over
![]() $W(S)$
. It is well defined up to unique isomorphism, in the usual sense. As remarked earlier, it is at this point clear that the construction
$W(S)$
. It is well defined up to unique isomorphism, in the usual sense. As remarked earlier, it is at this point clear that the construction
![]() $E/S\mapsto \widetilde{E}/W(S)$
for affine schemes
$E/S\mapsto \widetilde{E}/W(S)$
for affine schemes
![]() $S$
is compatible with base change and therefore can be extended to any ordinary elliptic curve over any
$S$
is compatible with base change and therefore can be extended to any ordinary elliptic curve over any
![]() $p$
-adic sheaf
$p$
-adic sheaf
![]() $S$
and we do so without further comment.
$S$
and we do so without further comment.
Our construction of the canonical lift
![]() $\widetilde{E}$
appears to depend on the auxiliary choice of the level
$\widetilde{E}$
appears to depend on the auxiliary choice of the level
![]() $N$
. One could easily show at this point that it does not, up to canonical isomorphism, but this is a consequence of the uniqueness statement proved in Section 6, and there is no need to establish it earlier.
$N$
. One could easily show at this point that it does not, up to canonical isomorphism, but this is a consequence of the uniqueness statement proved in Section 6, and there is no need to establish it earlier.
5.3 Remark: a stack-theoretic interpretation
The language of stacks is well-suited for expressing the descent argument above. For simplicity, we explain it for Witt vectors of finite length.
Given a stack
![]() $X$
, let
$X$
, let
![]() $W_{n\ast }(X)$
denote the fibered category sending any affine scheme
$W_{n\ast }(X)$
denote the fibered category sending any affine scheme
![]() $S$
to the category
$S$
to the category
![]() $X(W_{n}(S))$
. This is often called the arithmetic jet space or the Greenberg transform of
$X(W_{n}(S))$
. This is often called the arithmetic jet space or the Greenberg transform of
![]() $X$
. It is straightforward to show that
$X$
. It is straightforward to show that
![]() $W_{n\ast }$
sends affine schemes to affine schemes, that it is a right adjoint and hence sends groupoid objects to groupoid objects, and that it preserves étale morphisms. (See [Reference Borger4].) Finally, by the theorem in 3.2 the functor
$W_{n\ast }$
sends affine schemes to affine schemes, that it is a right adjoint and hence sends groupoid objects to groupoid objects, and that it preserves étale morphisms. (See [Reference Borger4].) Finally, by the theorem in 3.2 the functor
![]() $W_{n}$
is continuous in the étale topology. It then follows for general reasons that
$W_{n}$
is continuous in the étale topology. It then follows for general reasons that
![]() $W_{n\ast }$
takes stacks to stacks. (See [16, Tag 04WC].)
$W_{n\ast }$
takes stacks to stacks. (See [16, Tag 04WC].)
The compatible Frobenius lifts on
![]() $Y(N)^{\text{o}}$
and
$Y(N)^{\text{o}}$
and
![]() $Y(N,N)^{\text{o}}$
can then be packaged as a morphism of étale groupoid objects
$Y(N,N)^{\text{o}}$
can then be packaged as a morphism of étale groupoid objects
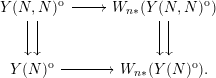
It therefore induces a morphism (unique up to unique isomorphism) of the quotient stacks

This morphism of stacks is then nothing more than the family of canonical lift functors, truncated at length
![]() $n$
. The image of an elliptic curve
$n$
. The image of an elliptic curve
![]() $E$
over
$E$
over
![]() $S$
is the elliptic curve
$S$
is the elliptic curve
![]() $\widetilde{E}_{W_{n}(S)}$
over
$\widetilde{E}_{W_{n}(S)}$
over
![]() $W_{n}(S)$
.
$W_{n}(S)$
.
It is worth noting that Buium’s work on differential modular forms [Reference Buium6] also touches on the connection between canonical lifts, moduli spaces, and arithmetic jet spaces.
5.4 Frobenius lifts
In this section, we define isomorphisms
where
![]() $F$
denotes the Frobenius map
$F$
denotes the Frobenius map
![]() $W(S)\rightarrow W(S)$
, such that the composition
$W(S)\rightarrow W(S)$
, such that the composition
with the quotient map is a Frobenius lift, in the sense of Section 4. First observe that such an isomorphism
![]() $\unicode[STIX]{x1D702}_{E}$
, if it exists, is necessarily unique. Indeed, to show two isomorphisms with the property above agree, it is enough to show they agree after base change to any
$\unicode[STIX]{x1D702}_{E}$
, if it exists, is necessarily unique. Indeed, to show two isomorphisms with the property above agree, it is enough to show they agree after base change to any
![]() $W_{n}(S_{i})$
, where
$W_{n}(S_{i})$
, where
![]() $S_{i}$
is any affine scheme mapping to
$S_{i}$
is any affine scheme mapping to
![]() $S$
on which
$S$
on which
![]() $p$
is nilpotent; but then the difference of two such maps would be a map of elliptic curves which is zero over
$p$
is nilpotent; but then the difference of two such maps would be a map of elliptic curves which is zero over
![]() $\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W_{n}(S_{i})$
, and hence zero over all of
$\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W_{n}(S_{i})$
, and hence zero over all of
![]() $W_{n}(S_{i})$
by the rigidity theorem [Reference Katz and Mazur12, Theorem 2.4.2, p. 76].
$W_{n}(S_{i})$
by the rigidity theorem [Reference Katz and Mazur12, Theorem 2.4.2, p. 76].
Therefore, local existence on the base will imply global existence. In particular, we may assume that
![]() $E$
admits a level-
$E$
admits a level-
![]() $N$
structure and then, by base change, that
$N$
structure and then, by base change, that
![]() $S=Y(N)^{\text{o}}$
and that
$S=Y(N)^{\text{o}}$
and that
![]() $E$
is the universal curve
$E$
is the universal curve
![]() $\mathscr{E}$
.
$\mathscr{E}$
.
The classifying morphism
![]() $c=\widetilde{\text{id}}:W(Y(N)^{\text{o}})\rightarrow Y(N)^{\text{o}}$
for
$c=\widetilde{\text{id}}:W(Y(N)^{\text{o}})\rightarrow Y(N)^{\text{o}}$
for
![]() $\widetilde{\mathscr{E}}$
is Frobenius equivariant, by construction. In other words, there is a unique identification
$\widetilde{\mathscr{E}}$
is Frobenius equivariant, by construction. In other words, there is a unique identification
![]() $c^{\ast }\unicode[STIX]{x1D713}^{\ast }(\mathscr{E})=\unicode[STIX]{x1D713}^{\ast }F^{\ast }(\mathscr{E})$
compatible with the level structure. We also have
$c^{\ast }\unicode[STIX]{x1D713}^{\ast }(\mathscr{E})=\unicode[STIX]{x1D713}^{\ast }F^{\ast }(\mathscr{E})$
compatible with the level structure. We also have
![]() $\unicode[STIX]{x1D713}^{\ast }(\mathscr{E})=\mathscr{E}/\mathscr{E}^{\text{can}}$
, by the definition of
$\unicode[STIX]{x1D713}^{\ast }(\mathscr{E})=\mathscr{E}/\mathscr{E}^{\text{can}}$
, by the definition of
![]() $\unicode[STIX]{x1D713}$
. Thus we have identifications
$\unicode[STIX]{x1D713}$
. Thus we have identifications
which are compatible with the level structure (and hence unique). Finally, the composition
![]() $\widetilde{\mathscr{E}}\rightarrow \widetilde{\mathscr{E}}/\widetilde{\mathscr{E}}^{\text{can}}=F^{\ast }(\widetilde{\mathscr{E}})$
reduces to the relative
$\widetilde{\mathscr{E}}\rightarrow \widetilde{\mathscr{E}}/\widetilde{\mathscr{E}}^{\text{can}}=F^{\ast }(\widetilde{\mathscr{E}})$
reduces to the relative
![]() $p$
th power Frobenius map modulo
$p$
th power Frobenius map modulo
![]() $p$
because, writing
$p$
because, writing
![]() $\widetilde{\mathscr{E}}_{0}=\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}\widetilde{\mathscr{E}}$
, the actual Frobenius map
$\widetilde{\mathscr{E}}_{0}=\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}\widetilde{\mathscr{E}}$
, the actual Frobenius map
![]() $\widetilde{\mathscr{E}}_{0}\rightarrow \text{Fr}^{\ast }(\widetilde{\mathscr{E}}_{0})$
has kernel
$\widetilde{\mathscr{E}}_{0}\rightarrow \text{Fr}^{\ast }(\widetilde{\mathscr{E}}_{0})$
has kernel
![]() $\widetilde{\mathscr{E}}_{0}^{\text{can}}$
and is compatible with the level structure.
$\widetilde{\mathscr{E}}_{0}^{\text{can}}$
and is compatible with the level structure.
From the stack-theoretic point of view, the map
![]() $\unicode[STIX]{x1D702}_{E}$
can be viewed as an invertible natural transformation
$\unicode[STIX]{x1D702}_{E}$
can be viewed as an invertible natural transformation
![]() $\unicode[STIX]{x1D713}\circ c\rightarrow c\circ F$
and hence as providing a Frobenius equivariant structure on the morphism
$\unicode[STIX]{x1D713}\circ c\rightarrow c\circ F$
and hence as providing a Frobenius equivariant structure on the morphism
![]() $c:W(S)\rightarrow Y(1)^{\text{o}}$
.
$c:W(S)\rightarrow Y(1)^{\text{o}}$
.
5.5 Remark: avoiding abstract sheaf theory
It is possible to avoid abstract sheaf theory by working with compatible systems of elliptic curves. Indeed, as explained in Sections 2.1 and 3.2, an elliptic curve over
![]() $W(S)$
, where
$W(S)$
, where
![]() $S$
is a scheme on which
$S$
is a scheme on which
![]() $p$
is nilpotent, is equivalent to a compatible family of elliptic curves over the
$p$
is nilpotent, is equivalent to a compatible family of elliptic curves over the
![]() $W_{n}(S)$
, which are also schemes on which
$W_{n}(S)$
, which are also schemes on which
![]() $p$
is nilpotent (and even of finite type over
$p$
is nilpotent (and even of finite type over
![]() $\mathbb{Z}_{p}$
if
$\mathbb{Z}_{p}$
if
![]() $S$
is). Thus the canonical lift
$S$
is). Thus the canonical lift
![]() $\widetilde{E}$
can be viewed as a compatible system of elliptic curves
$\widetilde{E}$
can be viewed as a compatible system of elliptic curves
![]() $\widetilde{E}_{n}$
over the schemes
$\widetilde{E}_{n}$
over the schemes
![]() $W_{n}(S)$
, which are not much harder to understand than
$W_{n}(S)$
, which are not much harder to understand than
![]() $S$
itself.
$S$
itself.
Of course one could construct this compatible system directly, without going through Witt vectors of infinite length. For each
![]() $n$
, the truncated canonical lift
$n$
, the truncated canonical lift
![]() $\widetilde{E}_{n}$
is constructed exactly as we did above with Witt vectors of infinite length but using
$\widetilde{E}_{n}$
is constructed exactly as we did above with Witt vectors of infinite length but using
![]() $W_{n}$
everywhere instead of
$W_{n}$
everywhere instead of
![]() $W$
. One then shows directly that the
$W$
. One then shows directly that the
![]() $\widetilde{E}_{n}$
form a compatible system, and we never have to leave the category of schemes. The Frobenius morphism then becomes a family of morphisms
$\widetilde{E}_{n}$
form a compatible system, and we never have to leave the category of schemes. The Frobenius morphism then becomes a family of morphisms
of elliptic curves over the
![]() $W_{n}(S)$
, where
$W_{n}(S)$
, where
![]() $F$
now denotes the truncated Witt vector Frobenius map
$F$
now denotes the truncated Witt vector Frobenius map
![]() $W_{n}(S)\rightarrow W_{n+1}(S)$
.
$W_{n}(S)\rightarrow W_{n+1}(S)$
.
6 Uniqueness
To prove the uniqueness part of the theorem, we need the following result in the particular case of the universal elliptic curve. But since the result is just as easy to prove in a more general form, we do that.
Theorem 6.1. Let
![]() $R$
be a
$R$
be a
![]() $p$
-adically complete ring such that
$p$
-adically complete ring such that
![]() $W(R)$
is
$W(R)$
is
![]() $p$
-torsion-free. Let
$p$
-torsion-free. Let
![]() $S=\operatorname{colim}_{n}\operatorname{Spec}R/p^{n+1}R$
, and let
$S=\operatorname{colim}_{n}\operatorname{Spec}R/p^{n+1}R$
, and let
![]() $E$
be an ordinary elliptic curve over
$E$
be an ordinary elliptic curve over
![]() $S$
. Suppose
$S$
. Suppose
![]() $X_{1}$
and
$X_{1}$
and
![]() $X_{2}$
are lifts of
$X_{2}$
are lifts of
![]() $E$
to
$E$
to
![]() $W(S)$
with Frobenius lifts
$W(S)$
with Frobenius lifts
![]() $\unicode[STIX]{x1D713}_{1}$
and
$\unicode[STIX]{x1D713}_{1}$
and
![]() $\unicode[STIX]{x1D713}_{2}$
. Then there is a unique Frobenius equivariant isomorphism
$\unicode[STIX]{x1D713}_{2}$
. Then there is a unique Frobenius equivariant isomorphism
![]() $\unicode[STIX]{x1D6FD}:X_{1}\rightarrow X_{2}$
restricting to the identity on
$\unicode[STIX]{x1D6FD}:X_{1}\rightarrow X_{2}$
restricting to the identity on
![]() $E$
.
$E$
.
We recall again that
![]() $W(R)$
is
$W(R)$
is
![]() $p$
-torsion-free if
$p$
-torsion-free if
![]() $R$
is either
$R$
is either
![]() $p$
-torsion-free or a perfect
$p$
-torsion-free or a perfect
![]() $\mathbb{F}_{p}$
-algebra. Also note that by formal GAGA, elliptic curves over
$\mathbb{F}_{p}$
-algebra. Also note that by formal GAGA, elliptic curves over
![]() $S$
are equivalent to elliptic curves over
$S$
are equivalent to elliptic curves over
![]() $\operatorname{Spec}R$
.
$\operatorname{Spec}R$
.
Proof. The Frobenius lifts are morphisms
![]() $X_{i}\rightarrow F^{\ast }(X_{i})$
of elliptic curves over
$X_{i}\rightarrow F^{\ast }(X_{i})$
of elliptic curves over
![]() $W(S)$
which reduce to the Frobenius map modulo
$W(S)$
which reduce to the Frobenius map modulo
![]() $p$
, and hence are (representable and) flat of degree
$p$
, and hence are (representable and) flat of degree
![]() $p$
, by rigidity [Reference Katz and Mazur12, Theorem 2.4.2, p. 76]. Therefore, the kernel is a (representable) finite flat lift of the kernel of the Frobenius map and hence equals the canonical subgroup. Thus the Frobenius lifts
$p$
, by rigidity [Reference Katz and Mazur12, Theorem 2.4.2, p. 76]. Therefore, the kernel is a (representable) finite flat lift of the kernel of the Frobenius map and hence equals the canonical subgroup. Thus the Frobenius lifts
![]() $\unicode[STIX]{x1D713}_{i}$
induce isomorphisms
$\unicode[STIX]{x1D713}_{i}$
induce isomorphisms
![]() $\bar{\unicode[STIX]{x1D713}}_{i}:X_{i}/X_{i}^{\text{can}}\overset{{\sim}}{\rightarrow }F^{\ast }(X_{i})$
.
$\bar{\unicode[STIX]{x1D713}}_{i}:X_{i}/X_{i}^{\text{can}}\overset{{\sim}}{\rightarrow }F^{\ast }(X_{i})$
.
We first consider the case where
![]() $E$
admits a level-
$E$
admits a level-
![]() $N$
structure
$N$
structure
![]() $\unicode[STIX]{x1D709}$
. Let
$\unicode[STIX]{x1D709}$
. Let
![]() $\unicode[STIX]{x1D709}_{i}$
denote the unique lift of
$\unicode[STIX]{x1D709}_{i}$
denote the unique lift of
![]() $\unicode[STIX]{x1D709}$
to
$\unicode[STIX]{x1D709}$
to
![]() $X_{i}$
, and let
$X_{i}$
, and let
![]() $\unicode[STIX]{x1D6FC}_{i}:W(S)\rightarrow Y(N)^{\text{o}}$
denote the classifying map for
$\unicode[STIX]{x1D6FC}_{i}:W(S)\rightarrow Y(N)^{\text{o}}$
denote the classifying map for
![]() $(X_{i},\unicode[STIX]{x1D709}_{i})$
. Now observe that the isomorphisms
$(X_{i},\unicode[STIX]{x1D709}_{i})$
. Now observe that the isomorphisms
![]() $\bar{\unicode[STIX]{x1D713}}_{i}$
must preserve the level structure, where
$\bar{\unicode[STIX]{x1D713}}_{i}$
must preserve the level structure, where
![]() $X_{i}/X_{i}^{\text{can}}$
is given the image level structure and
$X_{i}/X_{i}^{\text{can}}$
is given the image level structure and
![]() $F^{\ast }(X_{i})$
is given the pull-back level structure. Indeed, consider the elliptic curves
$F^{\ast }(X_{i})$
is given the pull-back level structure. Indeed, consider the elliptic curves
![]() $\bar{X}_{i}=\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}X_{i}$
over
$\bar{X}_{i}=\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}X_{i}$
over
![]() $\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W(S)$
. Because
$\operatorname{Spec}\mathbb{F}_{p}\times _{\operatorname{Spec}\mathbb{Z}}W(S)$
. Because
![]() $p\nmid N$
, the
$p\nmid N$
, the
![]() $N$
-torsion is finite étale. Therefore, the Frobenius map
$N$
-torsion is finite étale. Therefore, the Frobenius map
![]() $\bar{X}_{i}\rightarrow \text{Fr}_{S}^{\ast }(\bar{X}_{i})$
preserves the level structure and, again because the
$\bar{X}_{i}\rightarrow \text{Fr}_{S}^{\ast }(\bar{X}_{i})$
preserves the level structure and, again because the
![]() $N$
-torsion is finite étale, so does any lift of the Frobenius map. In particular, the maps
$N$
-torsion is finite étale, so does any lift of the Frobenius map. In particular, the maps
![]() $\bar{\unicode[STIX]{x1D713}}_{i}$
preserve it.
$\bar{\unicode[STIX]{x1D713}}_{i}$
preserve it.
It follows that the elliptic curves
![]() $X_{i}/X_{i}^{\text{can}}$
and
$X_{i}/X_{i}^{\text{can}}$
and
![]() $F^{\ast }(X_{i})$
have the same classifying map
$F^{\ast }(X_{i})$
have the same classifying map
![]() $W(S)\rightarrow Y(N)^{\text{o}}$
. The classifying map for
$W(S)\rightarrow Y(N)^{\text{o}}$
. The classifying map for
![]() $X_{i}/X_{i}^{\text{can}}$
is
$X_{i}/X_{i}^{\text{can}}$
is
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FC}_{i}$
, by the definition of
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FC}_{i}$
, by the definition of
![]() $\unicode[STIX]{x1D713}$
, and that for
$\unicode[STIX]{x1D713}$
, and that for
![]() $F^{\ast }(X_{i})$
is
$F^{\ast }(X_{i})$
is
![]() $\unicode[STIX]{x1D6FC}_{i}\circ F$
. Therefore, we have
$\unicode[STIX]{x1D6FC}_{i}\circ F$
. Therefore, we have
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FC}_{i}=\unicode[STIX]{x1D6FC}_{i}\circ F$
, which is to say that the maps
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D6FC}_{i}=\unicode[STIX]{x1D6FC}_{i}\circ F$
, which is to say that the maps
![]() $\unicode[STIX]{x1D6FC}_{i}:W(S)\rightarrow Y(N)^{\text{o}}$
commute with the Frobenius lifts.
$\unicode[STIX]{x1D6FC}_{i}:W(S)\rightarrow Y(N)^{\text{o}}$
commute with the Frobenius lifts.
But at the same time, since both
![]() $(X_{i},\unicode[STIX]{x1D709}_{i})$
lift
$(X_{i},\unicode[STIX]{x1D709}_{i})$
lift
![]() $(E,\unicode[STIX]{x1D709})$
, the two compositions
$(E,\unicode[STIX]{x1D709})$
, the two compositions
agree. Therefore, writing
![]() $Y(N)^{\text{o}}=\operatorname{colim}_{n}\operatorname{Spec}A/p^{n+1}A$
with
$Y(N)^{\text{o}}=\operatorname{colim}_{n}\operatorname{Spec}A/p^{n+1}A$
with
![]() $A$
$A$
![]() $p$
-adically complete, we see that the two compositions
$p$
-adically complete, we see that the two compositions
agree. Further, the maps
![]() $\unicode[STIX]{x1D6FC}_{1}^{\ast }$
and
$\unicode[STIX]{x1D6FC}_{1}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FC}_{2}^{\ast }$
are Frobenius equivariant because
$\unicode[STIX]{x1D6FC}_{2}^{\ast }$
are Frobenius equivariant because
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $\unicode[STIX]{x1D6FC}_{2}$
are. Since
$\unicode[STIX]{x1D6FC}_{2}$
are. Since
![]() $A$
and
$A$
and
![]() $W(R)$
are
$W(R)$
are
![]() $p$
-torsion-free, the universal property of Witt vectors implies
$p$
-torsion-free, the universal property of Witt vectors implies
![]() $\unicode[STIX]{x1D6FC}_{1}^{\ast }=\unicode[STIX]{x1D6FC}_{2}^{\ast }$
and hence
$\unicode[STIX]{x1D6FC}_{1}^{\ast }=\unicode[STIX]{x1D6FC}_{2}^{\ast }$
and hence
![]() $\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{2}$
.
$\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{2}$
.
When
![]() $E$
is arbitrary, the existence and uniqueness of
$E$
is arbitrary, the existence and uniqueness of
![]() $\unicode[STIX]{x1D6FD}$
follow formally because étale locally
$\unicode[STIX]{x1D6FD}$
follow formally because étale locally
![]() $\unicode[STIX]{x1D6FD}$
exists and is unique. We write out the details. Let
$\unicode[STIX]{x1D6FD}$
exists and is unique. We write out the details. Let
![]() $S^{\prime }$
denote the universal étale cover of
$S^{\prime }$
denote the universal étale cover of
![]() $S$
over which
$S$
over which
![]() $E$
admits a level-
$E$
admits a level-
![]() $N$
structure. Write
$N$
structure. Write
![]() $E^{\prime }=S^{\prime }\times _{S}E$
and
$E^{\prime }=S^{\prime }\times _{S}E$
and
![]() $X_{i}^{\prime }=W(S^{\prime })\times _{W(S)}E_{i}$
. Then each
$X_{i}^{\prime }=W(S^{\prime })\times _{W(S)}E_{i}$
. Then each
![]() $X_{i}^{\prime }$
is a lift of
$X_{i}^{\prime }$
is a lift of
![]() $E^{\prime }$
with a Frobenius lift
$E^{\prime }$
with a Frobenius lift
![]() $\unicode[STIX]{x1D713}_{i}^{\prime }=F\times \unicode[STIX]{x1D713}_{i}$
. Since each
$\unicode[STIX]{x1D713}_{i}^{\prime }=F\times \unicode[STIX]{x1D713}_{i}$
. Since each
![]() $X_{i}^{\prime }$
also admits a level-
$X_{i}^{\prime }$
also admits a level-
![]() $N$
structure, the construction above gives a canonical morphism
$N$
structure, the construction above gives a canonical morphism
![]() $\unicode[STIX]{x1D6FD}^{\prime }:X_{1}^{\prime }\rightarrow X_{2}^{\prime }$
(and hence in fact a unique one, because
$\unicode[STIX]{x1D6FD}^{\prime }:X_{1}^{\prime }\rightarrow X_{2}^{\prime }$
(and hence in fact a unique one, because
![]() $N$
is large) commuting with the Frobenius lifts
$N$
is large) commuting with the Frobenius lifts
![]() $\unicode[STIX]{x1D713}_{i}^{\prime }$
. Further,
$\unicode[STIX]{x1D713}_{i}^{\prime }$
. Further,
![]() $\unicode[STIX]{x1D6FD}$
is equivariant with respect to descent data. Indeed, write
$\unicode[STIX]{x1D6FD}$
is equivariant with respect to descent data. Indeed, write
![]() $S^{\prime \prime }=S^{\prime }\times _{S}S^{\prime }$
and
$S^{\prime \prime }=S^{\prime }\times _{S}S^{\prime }$
and
![]() $X_{i}^{\prime \prime }=W(S^{\prime \prime })\times _{W(S)}X$
. Then each
$X_{i}^{\prime \prime }=W(S^{\prime \prime })\times _{W(S)}X$
. Then each
![]() $X_{i}^{\prime \prime }$
is a lift of
$X_{i}^{\prime \prime }$
is a lift of
![]() $S^{\prime \prime }\times _{S}E$
with Frobenius lift
$S^{\prime \prime }\times _{S}E$
with Frobenius lift
![]() $\unicode[STIX]{x1D713}_{i}^{\prime \prime }=F\times \unicode[STIX]{x1D713}_{i}$
. Therefore, there is a unique Frobenius equivariant morphism
$\unicode[STIX]{x1D713}_{i}^{\prime \prime }=F\times \unicode[STIX]{x1D713}_{i}$
. Therefore, there is a unique Frobenius equivariant morphism
![]() $\unicode[STIX]{x1D6FD}^{\prime \prime }:X_{1}^{\prime \prime }\rightarrow X_{2}^{\prime \prime }$
. In particular, the two restrictions of
$\unicode[STIX]{x1D6FD}^{\prime \prime }:X_{1}^{\prime \prime }\rightarrow X_{2}^{\prime \prime }$
. In particular, the two restrictions of
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
to
$\unicode[STIX]{x1D6FD}^{\prime }$
to
![]() $W(S^{\prime \prime })$
agree, which is to say that
$W(S^{\prime \prime })$
agree, which is to say that
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
is equivariant with respect to descent data.
$\unicode[STIX]{x1D6FD}^{\prime }$
is equivariant with respect to descent data.
6.2 Uniqueness of the canonical lift functor
Suppose we have an assignment
![]() $E\mapsto \check{E}$
, sending elliptic curves
$E\mapsto \check{E}$
, sending elliptic curves
![]() $E/S$
to elliptic curves
$E/S$
to elliptic curves
![]() $\check{E}/W(S)$
with a Frobenius lift which is compatible with change of the base
$\check{E}/W(S)$
with a Frobenius lift which is compatible with change of the base
![]() $S$
. To give an isomorphism
$S$
. To give an isomorphism
![]() $\check{E}\rightarrow \widetilde{E}$
, it is enough give isomorphisms locally on
$\check{E}\rightarrow \widetilde{E}$
, it is enough give isomorphisms locally on
![]() $S$
which are compatible with change of
$S$
which are compatible with change of
![]() $S$
. Therefore, we may assume
$S$
. Therefore, we may assume
![]() $E$
admits a level-
$E$
admits a level-
![]() $N$
structure. Let
$N$
structure. Let
![]() $d:S\rightarrow Y(N)^{\text{o}}$
denote the classifying morphism of
$d:S\rightarrow Y(N)^{\text{o}}$
denote the classifying morphism of
![]() $E$
, and let
$E$
, and let
![]() $W(d):W(S)\rightarrow W(Y(N)^{\text{o}})$
denote the induced morphism. Now since we have
$W(d):W(S)\rightarrow W(Y(N)^{\text{o}})$
denote the induced morphism. Now since we have
![]() $Y(N)^{\text{o}}=\operatorname{colim}_{n}\operatorname{Spec}A_{N}/p^{n+1}A_{N}$
, where
$Y(N)^{\text{o}}=\operatorname{colim}_{n}\operatorname{Spec}A_{N}/p^{n+1}A_{N}$
, where
![]() $A_{N}$
is
$A_{N}$
is
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion-free, we can apply the theorem above to the universal ordinary elliptic curve
$p$
-torsion-free, we can apply the theorem above to the universal ordinary elliptic curve
![]() $\mathscr{E}$
over
$\mathscr{E}$
over
![]() $Y(N)^{\text{o}}$
. Therefore, there is a unique Frobenius equivariant isomorphism
$Y(N)^{\text{o}}$
. Therefore, there is a unique Frobenius equivariant isomorphism
![]() $\check{\mathscr{E}}\rightarrow \widetilde{\mathscr{E}}$
restricting to the identity on
$\check{\mathscr{E}}\rightarrow \widetilde{\mathscr{E}}$
restricting to the identity on
![]() $\mathscr{E}$
. Since the constructions
$\mathscr{E}$
. Since the constructions
![]() $E\mapsto \check{E}$
and
$E\mapsto \check{E}$
and
![]() $E\mapsto \widetilde{E}$
are compatible with restriction of
$E\mapsto \widetilde{E}$
are compatible with restriction of
![]() $S$
(in the first case by assumption and in the second case by Section 5), the family of morphisms
$S$
(in the first case by assumption and in the second case by Section 5), the family of morphisms
is the unique family of Frobenius equivariant isomorphisms
![]() $\check{E}\rightarrow \widetilde{E}$
which is compatible with restriction of
$\check{E}\rightarrow \widetilde{E}$
which is compatible with restriction of
![]() $S$
.
$S$
.
In particular, the functor
![]() $E\mapsto \widetilde{E}$
constructed in Section 5 is independent of the choice of the level
$E\mapsto \widetilde{E}$
constructed in Section 5 is independent of the choice of the level
![]() $N$
, up to unique isomorphism.
$N$
, up to unique isomorphism.
7 Remarks and applications
7.1 Comparison with the classical canonical lifts
In the classical context where
![]() $S=\operatorname{Spec}k$
with
$S=\operatorname{Spec}k$
with
![]() $k$
a perfect field of characteristic
$k$
a perfect field of characteristic
![]() $p$
, it is known that the Serre–Tate canonical lift has a Frobenius lift and is characterized, up to unique isomorphism, by this property. (See Messing’s book [Reference Messing15, p. 177, cor. (1.2) and p. 174, cor. (3.4)].) The theorem in Theorem 6.1 then implies that our canonical lifts are isomorphic to the Serre–Tate canonical lifts by a unique Frobenius equivariant morphism.
$p$
, it is known that the Serre–Tate canonical lift has a Frobenius lift and is characterized, up to unique isomorphism, by this property. (See Messing’s book [Reference Messing15, p. 177, cor. (1.2) and p. 174, cor. (3.4)].) The theorem in Theorem 6.1 then implies that our canonical lifts are isomorphic to the Serre–Tate canonical lifts by a unique Frobenius equivariant morphism.
Also observe that in this context, we only need a weak case of the theorem in Section 3.2 in the descent argument. This is because level structure exists over some finite extension
![]() $k^{\prime }/k$
, and then it is well known that
$k^{\prime }/k$
, and then it is well known that
![]() $W(k^{\prime })/W(k)$
is finite étale and we have
$W(k^{\prime })/W(k)$
is finite étale and we have
![]() $W(k^{\prime }\otimes _{k}k^{\prime })=W(k^{\prime })\otimes _{W(k)}W(k^{\prime })$
. Thus in the classical context, our argument really is little more than an application of the universal property of Witt vectors.
$W(k^{\prime }\otimes _{k}k^{\prime })=W(k^{\prime })\otimes _{W(k)}W(k^{\prime })$
. Thus in the classical context, our argument really is little more than an application of the universal property of Witt vectors.
While our approach has the benefit of allowing families in mixed characteristic, it also requires them, even if one is only interested in canonical lifts of elliptic curves in characteristic
![]() $p$
; and this could be viewed as a drawback. The reason is simply that the special fiber
$p$
; and this could be viewed as a drawback. The reason is simply that the special fiber
![]() $Y(N)_{\mathbb{F}_{p}}^{\text{o}}$
does not admit a map from
$Y(N)_{\mathbb{F}_{p}}^{\text{o}}$
does not admit a map from
![]() $W(Y(N)_{\mathbb{F}_{p}}^{\text{o}})$
. Indeed, no nonempty Witt vector scheme maps to
$W(Y(N)_{\mathbb{F}_{p}}^{\text{o}})$
. Indeed, no nonempty Witt vector scheme maps to
![]() $\operatorname{Spec}\mathbb{F}_{p}$
.
$\operatorname{Spec}\mathbb{F}_{p}$
.
7.2
 $j$
-invariants
$j$
-invariants
We can describe the
![]() $j$
-invariant of the canonical lift of the universal family. Recall that
$j$
-invariant of the canonical lift of the universal family. Recall that
![]() $Y(N)^{\text{o}}=\operatorname{Spf}A_{N}$
and
$Y(N)^{\text{o}}=\operatorname{Spf}A_{N}$
and
![]() $Y(N,N)^{\text{o}}=\operatorname{Spf}A_{N,N}$
, where
$Y(N,N)^{\text{o}}=\operatorname{Spf}A_{N,N}$
, where
![]() $A_{N}$
and
$A_{N}$
and
![]() $A_{N,N}$
are
$A_{N,N}$
are
![]() $p$
-adically complete and
$p$
-adically complete and
![]() $p$
-torsion-free, and that forgetting the level structures induces a pair of Frobenius equivariant maps
$p$
-torsion-free, and that forgetting the level structures induces a pair of Frobenius equivariant maps
![]() $A_{N}\rightrightarrows A_{N,N}$
. Thus, writing
$A_{N}\rightrightarrows A_{N,N}$
. Thus, writing
![]() $A_{1}$
for the equalizer of these two maps, the map
$A_{1}$
for the equalizer of these two maps, the map
![]() $(\text{id}_{A_{N}})^{{\sim}}:A_{N}\rightarrow W(A_{N})$
restricts to a map
$(\text{id}_{A_{N}})^{{\sim}}:A_{N}\rightarrow W(A_{N})$
restricts to a map
![]() $s:A_{1}\rightarrow W(A_{1})$
, and so the Frobenius lift on
$s:A_{1}\rightarrow W(A_{1})$
, and so the Frobenius lift on
![]() $A_{N}$
restricts to a Frobenius lift on
$A_{N}$
restricts to a Frobenius lift on
![]() $A_{1}$
. Now write
$A_{1}$
. Now write
![]() $A_{1}=\mathbb{Z}_{p}[j,1/f(j)]^{\wedge }$
, where
$A_{1}=\mathbb{Z}_{p}[j,1/f(j)]^{\wedge }$
, where
![]() $j$
is an indeterminate identified with the
$j$
is an indeterminate identified with the
![]() $j$
-function,
$j$
-function,
![]() $f(j)$
is a monic polynomial whose roots lift the supersingular
$f(j)$
is a monic polynomial whose roots lift the supersingular
![]() $j$
-invariants, and
$j$
-invariants, and
![]() $(\cdot )^{\wedge }$
denotes
$(\cdot )^{\wedge }$
denotes
![]() $p$
-adic completion. The image of
$p$
-adic completion. The image of
![]() $j$
under the map
$j$
under the map
![]() $s:A_{1}\rightarrow W(A_{1})$
has ghost components
$s:A_{1}\rightarrow W(A_{1})$
has ghost components
![]() $\langle j,\unicode[STIX]{x1D713}(j),\unicode[STIX]{x1D713}^{\circ 2}(j),\ldots \,\rangle \in A_{1}^{\infty }$
. It follows that if
$\langle j,\unicode[STIX]{x1D713}(j),\unicode[STIX]{x1D713}^{\circ 2}(j),\ldots \,\rangle \in A_{1}^{\infty }$
. It follows that if
![]() $E$
is any family of ordinary elliptic curves, the ghost components of
$E$
is any family of ordinary elliptic curves, the ghost components of
![]() $j(\widetilde{E})$
are obtained by evaluating the universal expressions
$j(\widetilde{E})$
are obtained by evaluating the universal expressions
![]() $\unicode[STIX]{x1D713}^{\circ n}(j)\in \mathbb{Z}_{p}[j,1/f(j)]^{\wedge }$
at
$\unicode[STIX]{x1D713}^{\circ n}(j)\in \mathbb{Z}_{p}[j,1/f(j)]^{\wedge }$
at
![]() $j=j(E)$
.
$j=j(E)$
.
One can similarly consider the usual Witt components
![]() $(j_{0},j_{1},\ldots \,)$
of
$(j_{0},j_{1},\ldots \,)$
of
![]() $s(j)$
. Then the Witt components of
$s(j)$
. Then the Witt components of
![]() $j(\widetilde{E})$
are also obtained by evaluating the universal expressions
$j(\widetilde{E})$
are also obtained by evaluating the universal expressions
![]() $j_{n}\in \mathbb{Z}_{p}[j,1/f(j)]^{\wedge }$
at
$j_{n}\in \mathbb{Z}_{p}[j,1/f(j)]^{\wedge }$
at
![]() $j=j(E)$
. For example, by the definition of the ghost map, we have
$j=j(E)$
. For example, by the definition of the ghost map, we have
![]() $\unicode[STIX]{x1D713}^{\circ n}(j)=\sum _{i=0}^{n}p^{i}j_{i}^{p^{n-i}}$
, and so the Witt components of the
$\unicode[STIX]{x1D713}^{\circ n}(j)=\sum _{i=0}^{n}p^{i}j_{i}^{p^{n-i}}$
, and so the Witt components of the
![]() $j$
-invariant of the canonical lift of an elliptic curve with
$j$
-invariant of the canonical lift of an elliptic curve with
![]() $j$
-invariant
$j$
-invariant
![]() $j$
are given by
$j$
are given by
and so on. For elliptic curves over perfect fields of characteristic
![]() $p$
, such a result was found by Erdoğan [Reference Erdoğan7] (strengthening earlier results of Finotti [Reference Finotti8]) by more traditional means, but where the universal expressions are of course the reductions of ours modulo
$p$
, such a result was found by Erdoğan [Reference Erdoğan7] (strengthening earlier results of Finotti [Reference Finotti8]) by more traditional means, but where the universal expressions are of course the reductions of ours modulo
![]() $p$
. We note that Erdoğan also constructs canonical lifts for families over perfect
$p$
. We note that Erdoğan also constructs canonical lifts for families over perfect
![]() $\mathbb{F}_{p}$
-algebras.
$\mathbb{F}_{p}$
-algebras.
We can do the same for elliptic curves over a general base. Let
![]() $E$
be a family over
$E$
be a family over
![]() $\operatorname{Spf}R$
for a
$\operatorname{Spf}R$
for a
![]() $p$
-adically complete ring
$p$
-adically complete ring
![]() $R$
. Then the
$R$
. Then the
![]() $j$
-invariant
$j$
-invariant
![]() $j(\widetilde{E})$
is an element of
$j(\widetilde{E})$
is an element of
![]() $W(R)$
, and as in (3.1.1) its ghost components are
$W(R)$
, and as in (3.1.1) its ghost components are
where
![]() $E_{0}=E$
and
$E_{0}=E$
and
![]() $E_{n+1}=E_{n}/E_{n}^{\text{can}}$
. This already determines
$E_{n+1}=E_{n}/E_{n}^{\text{can}}$
. This already determines
![]() $j(\widetilde{E})$
if
$j(\widetilde{E})$
if
![]() $R$
is
$R$
is
![]() $p$
-torsion-free, since in that case the ghost map
$p$
-torsion-free, since in that case the ghost map
![]() $W(R)\rightarrow R^{\mathbb{N}}$
is injective. In general, one can lift
$W(R)\rightarrow R^{\mathbb{N}}$
is injective. In general, one can lift
![]() $E$
arbitrarily to a family
$E$
arbitrarily to a family
![]() $E^{\prime }$
over a
$E^{\prime }$
over a
![]() $p$
-torsion-free extension
$p$
-torsion-free extension
![]() $R^{\prime }$
of
$R^{\prime }$
of
![]() $R$
, and then
$R$
, and then
![]() $j(\widetilde{E})$
is the image under
$j(\widetilde{E})$
is the image under
![]() $W(R^{\prime })\rightarrow W(R)$
of
$W(R^{\prime })\rightarrow W(R)$
of
![]() $j((E^{\prime })^{{\sim}})$
, which has the simple description above since
$j((E^{\prime })^{{\sim}})$
, which has the simple description above since
![]() $R^{\prime }$
is
$R^{\prime }$
is
![]() $p$
-torsion-free.
$p$
-torsion-free.
This can be expressed in an especially pleasant way in the particular case where
![]() $R$
is a perfect
$R$
is a perfect
![]() $\mathbb{F}_{p}$
-algebra
$\mathbb{F}_{p}$
-algebra
![]() $k$
, and
$k$
, and
![]() $R^{\prime }$
is
$R^{\prime }$
is
![]() $W(k)$
. Then one can show that the projection
$W(k)$
. Then one can show that the projection
![]() $W(\text{pr}_{0}):W(W(k))\rightarrow W(k)$
sends a Witt vector with ghost components
$W(\text{pr}_{0}):W(W(k))\rightarrow W(k)$
sends a Witt vector with ghost components
![]() $\langle a_{0},a_{1},\ldots \,\rangle \in W(k)^{\infty }$
to
$\langle a_{0},a_{1},\ldots \,\rangle \in W(k)^{\infty }$
to
![]() $\lim _{n\rightarrow \infty }F^{-n}(a_{n})\in W(k)$
, and so we have
$\lim _{n\rightarrow \infty }F^{-n}(a_{n})\in W(k)$
, and so we have
where
![]() $E^{\prime }$
is an arbitrary lift to
$E^{\prime }$
is an arbitrary lift to
![]() $W(k)$
of
$W(k)$
of
![]() $E$
and the
$E$
and the
![]() $E_{n}^{\prime }$
are as above. If
$E_{n}^{\prime }$
are as above. If
![]() $k$
is a field with
$k$
is a field with
![]() $p^{r}$
elements, then
$p^{r}$
elements, then
![]() $F^{r}=\text{id}_{W(k)}$
and so we simply have
$F^{r}=\text{id}_{W(k)}$
and so we simply have
![]() $j(\widetilde{E})=\lim _{n\rightarrow \infty }j(E_{rn}^{\prime })$
.
$j(\widetilde{E})=\lim _{n\rightarrow \infty }j(E_{rn}^{\prime })$
.
7.3 Canonical lifts of canonical lifts
Amusingly, one can take canonical lifts of canonical lifts and so on, any number of times. Indeed, if
![]() $E$
is an ordinary elliptic curve over a
$E$
is an ordinary elliptic curve over a
![]() $p$
-adic sheaf
$p$
-adic sheaf
![]() $S$
, then
$S$
, then
![]() $\widetilde{E}$
is also an ordinary elliptic curve over the
$\widetilde{E}$
is also an ordinary elliptic curve over the
![]() $p$
-adic sheaf
$p$
-adic sheaf
![]() $W(S)$
. However, one can show that the double canonical lift
$W(S)$
. However, one can show that the double canonical lift
![]() $\widetilde{\widetilde{E}}$
is canonically isomorphic to the pull-back of
$\widetilde{\widetilde{E}}$
is canonically isomorphic to the pull-back of
![]() $\widetilde{E}$
through the composition, or plethysm, map
$\widetilde{E}$
through the composition, or plethysm, map
![]() $W(W(S))\rightarrow W(S)$
of [Reference Borger4, (10.6.13)], and similarly for the higher iterates. So these higher canonical lifts are all determined by the first one in a way that has nothing to do with elliptic curves and only the general theory of Witt vectors.
$W(W(S))\rightarrow W(S)$
of [Reference Borger4, (10.6.13)], and similarly for the higher iterates. So these higher canonical lifts are all determined by the first one in a way that has nothing to do with elliptic curves and only the general theory of Witt vectors.
7.4 Epilogue: on a general theory of canonical lifts
We proposed above that a theory of canonical lifts for a class of objects parametrized by a moduli space
![]() $Y$
should be defined to be a Frobenius lift
$Y$
should be defined to be a Frobenius lift
![]() $\unicode[STIX]{x1D713}:Y\rightarrow Y$
, as long as
$\unicode[STIX]{x1D713}:Y\rightarrow Y$
, as long as
![]() $Y$
is
$Y$
is
![]() $p$
-torsion-free. In the absence of this assumption, one should define a theory of canonical lifts to be a slightly stronger structure. Namely, the functor
$p$
-torsion-free. In the absence of this assumption, one should define a theory of canonical lifts to be a slightly stronger structure. Namely, the functor
![]() $W_{\ast }=\lim _{n}W_{n\ast }$
has a natural comonad structure (coming from the maps
$W_{\ast }=\lim _{n}W_{n\ast }$
has a natural comonad structure (coming from the maps
![]() $W_{m+n\ast }\rightarrow W_{m\ast }\circ W_{n\ast }$
of [Reference Borger4, (10.6.14)]) and a theory of canonical lifts for the objects parametrized by
$W_{m+n\ast }\rightarrow W_{m\ast }\circ W_{n\ast }$
of [Reference Borger4, (10.6.14)]) and a theory of canonical lifts for the objects parametrized by
![]() $Y$
would then be a coaction of the comonad
$Y$
would then be a coaction of the comonad
![]() $W_{\ast }$
on
$W_{\ast }$
on
![]() $Y$
. This is called a
$Y$
. This is called a
![]() $\unicode[STIX]{x1D6FF}$
-structure in Joyal [Reference Joyal10] and Buium [Reference Buium5] and a
$\unicode[STIX]{x1D6FF}$
-structure in Joyal [Reference Joyal10] and Buium [Reference Buium5] and a
![]() $p$
-typical
$p$
-typical
![]() $\unicode[STIX]{x1D6EC}$
-structure in [Reference Borger3, Reference Borger4].
$\unicode[STIX]{x1D6EC}$
-structure in [Reference Borger3, Reference Borger4].
This can also be done for other varieties of Witt vectors in the sense of [Reference Borger4], such as the big Witt vectors. One would then define a theory of canonical lifts, relative to the given variety of Witt vectors, to be an action of the comonad
![]() $W_{\ast }$
on
$W_{\ast }$
on
![]() $Y$
. In other words, a theory of canonical lifts for a class of objects should defined to be a
$Y$
. In other words, a theory of canonical lifts for a class of objects should defined to be a
![]() $\unicode[STIX]{x1D6EC}$
-structure on their moduli space. This was carried out by the second author [Reference Gurney9] in the case of elliptic curves with complex multiplication and the variety of big Witt vectors associated with an imaginary quadratic field.
$\unicode[STIX]{x1D6EC}$
-structure on their moduli space. This was carried out by the second author [Reference Gurney9] in the case of elliptic curves with complex multiplication and the variety of big Witt vectors associated with an imaginary quadratic field.