No CrossRef data available.
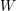 $W$-GRAPHS
$W$-GRAPHSPublished online by Cambridge University Press: 17 July 2018
A canonical basis in the sense of Lusztig is a basis of a free module over a ring of Laurent polynomials that is invariant under a certain semilinear involution and is obtained from a fixed “standard basis” through a triangular base change matrix with polynomial entries whose constant terms equal the identity matrix. Among the better known examples of canonical bases are the Kazhdan–Lusztig basis of Iwahori–Hecke algebras (see Kazhdan and Lusztig, Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (1979), 165–184), Lusztig’s canonical basis of quantum groups (see Lusztig, Canonical bases arising from quantized enveloping algebras, J. Amer. Math. Soc. 3(2) (1990), 447–498) and the Howlett–Yin basis of induced 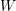 $W$-graph modules (see Howlett and Yin, Inducing W-graphs I, Math. Z. 244(2) (2003), 415–431; Inducing W-graphs II, Manuscripta Math. 115(4) (2004), 495–511). This paper has two major theoretical goals: first to show that having bases is superfluous in the sense that canonicalization can be generalized to nonfree modules. This construction is functorial in the appropriate sense. The second goal is to show that Howlett–Yin induction of
$W$-graph modules (see Howlett and Yin, Inducing W-graphs I, Math. Z. 244(2) (2003), 415–431; Inducing W-graphs II, Manuscripta Math. 115(4) (2004), 495–511). This paper has two major theoretical goals: first to show that having bases is superfluous in the sense that canonicalization can be generalized to nonfree modules. This construction is functorial in the appropriate sense. The second goal is to show that Howlett–Yin induction of 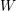 $W$-graphs is well-behaved a functor between module categories of
$W$-graphs is well-behaved a functor between module categories of 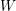 $W$-graph algebras that satisfies various properties one hopes for when a functor is called “induction,” for example transitivity and a Mackey theorem.
$W$-graph algebras that satisfies various properties one hopes for when a functor is called “induction,” for example transitivity and a Mackey theorem.