A canonical basis in the sense of Lusztig is a basis of a free module over a ring of Laurent polynomials that is invariant under a certain semilinear involution and is obtained from a fixed “standard basis” through a triangular base change matrix with polynomial entries whose constant terms equal the identity matrix. Among the better known examples of canonical bases are the Kazhdan–Lusztig basis of Iwahori–Hecke algebras (see Kazhdan and Lusztig, Representations of Coxeter groups and Hecke algebras, Invent. Math. 53 (1979), 165–184), Lusztig’s canonical basis of quantum groups (see Lusztig, Canonical bases arising from quantized enveloping algebras, J. Amer. Math. Soc. 3(2) (1990), 447–498) and the Howlett–Yin basis of induced W$W$-graph modules (see Howlett and Yin, Inducing W-graphs I, Math. Z. 244(2) (2003), 415–431; Inducing W-graphs II, Manuscripta Math. 115(4) (2004), 495–511). This paper has two major theoretical goals: first to show that having bases is superfluous in the sense that canonicalization can be generalized to nonfree modules. This construction is functorial in the appropriate sense. The second goal is to show that Howlett–Yin induction of W$W$-graphs is well-behaved a functor between module categories of W$W$-graph algebras that satisfies various properties one hopes for when a functor is called “induction,” for example transitivity and a Mackey theorem.

We give new estimates of lengths of extremal rays of birational type for toric varieties. We can see that our new estimates are the best by constructing some examples explicitly. As applications, we discuss the nefness and pseudo-effectivity of adjoint bundles of projective toric varieties. We also treat some generalizations of Fujita’s freeness and very ampleness for toric varieties.

In this article, we prove a finiteness result on the number of log minimal models for 3-folds in \operatorname{char}p>5$\operatorname{char}p>5$. We then use this result to prove a version of Batyrev’s conjecture on the structure of nef cone of curves on 3-folds in characteristic p>5$p>5$. We also give a proof of the same conjecture in full generality in characteristic 0. We further verify that the duality of movable curves and pseudo-effective divisors hold in arbitrary characteristic. We then give a criterion for the pseudo-effectiveness of the canonical divisor K_{X}$K_{X}$ of a smooth projective variety in arbitrary characteristic in terms of the existence of a family of rational curves on X$X$.

For a hyper-Kähler manifold deformation equivalent to a generalized Kummer manifold, we prove that the action of the automorphism group on the total Betti cohomology group is faithful. This is a sort of generalization of a work of Beauville and a more recent work of Boissière, Nieper-Wisskirchen, and Sarti, concerning the action of the automorphism group of a generalized Kummer manifold on the second cohomology group.

This paper will be devoted to study a class of bilinear square-function Fourier multiplier operator associated with a symbol m$m$ defined by

\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{T}_{\unicode[STIX]{x1D706},m}(f_{1},f_{2})(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg|\int _{(\mathbb{R}^{n})^{2}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})\,d\unicode[STIX]{x1D709}_{1}\,d\unicode[STIX]{x1D709}_{2}\bigg|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2}.\nonumber\end{eqnarray} $$\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{T}_{\unicode[STIX]{x1D706},m}(f_{1},f_{2})(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg|\int _{(\mathbb{R}^{n})^{2}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})\,d\unicode[STIX]{x1D709}_{1}\,d\unicode[STIX]{x1D709}_{2}\bigg|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2}.\nonumber\end{eqnarray}$$

\mathfrak{T}_{\unicode[STIX]{x1D706},m}$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$

g_{\unicode[STIX]{x1D706}}^{\ast }$g_{\unicode[STIX]{x1D706}}^{\ast }$

\mathfrak{T}_{\unicode[STIX]{x1D706},m}$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$

L\log L$L\log L$

\mathfrak{T}_{\unicode[STIX]{x1D706},m}$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$

We prove the L^{2}$L^{2}$ extension theorem for jets with optimal estimate following the method of Berndtsson–Lempert. For this purpose, following Demailly’s construction, we consider Hermitian metrics on jet vector bundles.

In 2005, using a famous lemma of Atkin and Swinnerton-Dyer (Some properties of partitions, Proc. Lond. Math. Soc. (3) 4 (1954), 84–106), Yesilyurt (Four identities related to third order mock theta functions in Ramanujan’s lost notebook, Adv. Math. 190 (2005), 278–299) proved four identities for third order mock theta functions found on pages 2 and 17 in Ramanujan’s lost notebook. The primary purpose of this paper is to offer new proofs in the spirit of what Ramanujan might have given in the hope that a better understanding of the identities might be gained. Third order mock theta functions are intimately connected with ranks of partitions. We prove new dissections for two rank generating functions, which are keys to our proof of the fourth, and the most difficult, of Ramanujan’s identities. In the last section of this paper, we establish new relations for ranks arising from our dissections of rank generating functions.

In this paper, we perform a detailed spectral study of the liberation process associated with two symmetries of arbitrary ranks: (R,S)\mapsto (R,U_{t}SU_{t}^{\ast })_{t\geqslant 0}$(R,S)\mapsto (R,U_{t}SU_{t}^{\ast })_{t\geqslant 0}$, where (U_{t})_{t\geqslant 0}$(U_{t})_{t\geqslant 0}$ is a free unitary Brownian motion freely independent from \{R,S\}$\{R,S\}$. Our main tool is free stochastic calculus which allows to derive a partial differential equation (PDE) for the Herglotz transform of the unitary process defined by Y_{t}:=RU_{t}SU_{t}^{\ast }$Y_{t}:=RU_{t}SU_{t}^{\ast }$. It turns out that this is exactly the PDE governing the flow of an analytic function transform of the spectral measure of the operator X_{t}:=PU_{t}QU_{t}^{\ast }P$X_{t}:=PU_{t}QU_{t}^{\ast }P$ where P,Q$P,Q$ are the orthogonal projections associated to R,S$R,S$. Next, we relate the two spectral measures of RU_{t}SU_{t}^{\ast }$RU_{t}SU_{t}^{\ast }$ and of PU_{t}QU_{t}^{\ast }P$PU_{t}QU_{t}^{\ast }P$ via their moment sequences and use this relationship to develop a theory of subordination for the boundary values of the Herglotz transform. In particular, we explicitly compute the subordinate function and extend its inverse continuously to the unit circle. As an application, we prove the identity i^{\ast }(\mathbb{C}P+\mathbb{C}(I-P);\mathbb{C}Q+\mathbb{C}(I-Q))=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$i^{\ast }(\mathbb{C}P+\mathbb{C}(I-P);\mathbb{C}Q+\mathbb{C}(I-Q))=-\unicode[STIX]{x1D712}_{\text{orb}}(P,Q)$.

A comprehensive study of the generalized Lambert series 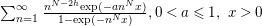\sum _{n=1}^{\infty }\frac{n^{N-2h}\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)},0<a\leqslant 1,~x>0$\sum _{n=1}^{\infty }\frac{n^{N-2h}\text{exp}(-an^{N}x)}{1-\text{exp}(-n^{N}x)},0<a\leqslant 1,~x>0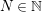$, N\in \mathbb{N}$N\in \mathbb{N}$ and 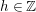h\in \mathbb{Z}$h\in \mathbb{Z}$, is undertaken. Several new transformations of this series are derived using a deep result on Raabe’s cosine transform that we obtain here. Three of these transformations lead to two-parameter generalizations of Ramanujan’s famous formula for 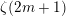\unicode[STIX]{x1D701}(2m+1)$\unicode[STIX]{x1D701}(2m+1)$ for 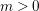m>0$m>0$, the transformation formula for the logarithm of the Dedekind eta function and Wigert’s formula for 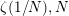\unicode[STIX]{x1D701}(1/N),N$\unicode[STIX]{x1D701}(1/N),N$ even. Numerous important special cases of our transformations are derived, for example, a result generalizing the modular relation between the Eisenstein series 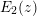E_{2}(z)$E_{2}(z)$ and 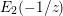E_{2}(-1/z)$E_{2}(-1/z)$. An identity relating 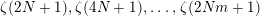\unicode[STIX]{x1D701}(2N+1),\unicode[STIX]{x1D701}(4N+1),\ldots ,\unicode[STIX]{x1D701}(2Nm+1)$\unicode[STIX]{x1D701}(2N+1),\unicode[STIX]{x1D701}(4N+1),\ldots ,\unicode[STIX]{x1D701}(2Nm+1)$ is obtained for 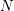N$N$ odd and 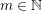m\in \mathbb{N}$m\in \mathbb{N}$. In particular, this gives a beautiful relation between 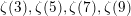\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$\unicode[STIX]{x1D701}(3),\unicode[STIX]{x1D701}(5),\unicode[STIX]{x1D701}(7),\unicode[STIX]{x1D701}(9)$ and 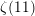\unicode[STIX]{x1D701}(11)$\unicode[STIX]{x1D701}(11)$. New results involving infinite series of hyperbolic functions with 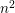n^{2}$n^{2}$ in their arguments, which are analogous to those of Ramanujan and Klusch, are obtained.

We investigate the Galois structures of p$p$-adic cohomology groups of general p$p$-adic representations over finite extensions of number fields. We show, in particular, that as the field extensions vary over natural families the Galois modules formed by these cohomology groups always decompose as the direct sum of a projective module and a complementary module of bounded p$p$-rank. We use this result to derive new (upper and lower) bounds on the changes in ranks of Selmer groups over extensions of number fields and descriptions of the explicit Galois structures of natural arithmetic modules.

We establish the continuity of Hilbert–Kunz multiplicity and F-signature as functions from a Cohen–Macaulay local ring (R,\mathfrak{m},k)$(R,\mathfrak{m},k)$ of prime characteristic to the real numbers at reduced parameter elements with respect to the \mathfrak{m}$\mathfrak{m}$-adic topology.

In this paper, we will prove that any \mathbb{A}^{3}$\mathbb{A}^{3}$-form over a field k$k$ of characteristic zero is trivial provided it has a locally nilpotent derivation satisfying certain properties. We will also show that the result of Kambayashi on the triviality of separable \mathbb{A}^{2}$\mathbb{A}^{2}$-forms over a field k$k$ extends to \mathbb{A}^{2}$\mathbb{A}^{2}$-forms over any one-dimensional Noetherian domain containing \mathbb{Q}$\mathbb{Q}$.