Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T05:06:35.786Z Has data issue: false hasContentIssue false
  • English
  • Français

On similar short sums

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  26 February 2010

N. Watt
N. Watt
Affiliation:
45 Charles Way, Limekilns, Fife. KY11 3LH, United Kingdom
Get access

Extract

In the paper [5] bounds are found for the sum,

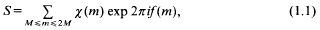
for a suitable Dirichlet character χ mod r, and real functionf(x). The proofs in that paper use Bombieri and Iwaniec's method [1], one formulation of which has as part of its first step the estimation of S in terms of a sum of many shorter sums of the form,

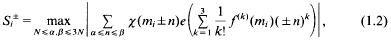
where e(x) = exp (2πix), mi∈ [M, 2M], and each mi, lies in its own interval, of length N ≥ M/4, that is disjoint from those of the others. This paper addresses a problem springing from above: to bound the numbers of ‘similar’ pairs, Si+, Si+, satisfying both

and

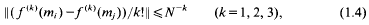
where ‖x‖ = min{|x − n|: n ∈ ℤ}. Lemma 5.2.1 of [3] (partial summation) shows that each sum in a similar pair is a bounded multiple of the other.

MSC classification

Secondary: 11L40: Estimates on character sums
Type
Research Article
Information
Mathematika , Volume 46 , Issue 1 , June 1999 , pp. 193 - 204
Copyright
Copyright © University College London 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bombieri, E. and Iwaniec, H.. On the order of ζ(½†it). Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4), 13 (1986), 449–472.Google Scholar
2.Huxley, M. N.Exponential sums and the Riemann zeta function IV. Proc. London Math. Soc. (3), 66 (1993), 1–40.CrossRefGoogle Scholar
3.Huxley, M. N.Area, Lattice Points, and Exponential Sums. London Math. Soc. Monographs, 13 (Oxford University Press, 1996).CrossRefGoogle Scholar
4.Huxley, M. N. and Watt, N.. Exponential sums and the Riemann zeta function. Proc. London Math. Soc. (3), 57 (1988), 1–24CrossRefGoogle Scholar
5.Huxley, M. N. and Watt, N. Hybrid bounds for Dirichlet's L-function. To appear in Math. Proc. Cam. Phil. Soc..Google Scholar
6.Watt, N.. Exponential sums and the Riemann zeta-function II. J. London Math. Soc. (2), 39 (1989), 385–404.CrossRefGoogle Scholar