Research Article
Isotropic surface area measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
-
- Article
- Export citation
The lower bound theorem for centrally symmetric simple polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-240
-
- Article
- Export citation
Families of congruent curves and applications
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 241-252
-
- Article
- Export citation
Convex intersection bodies in three and four dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-27
-
- Article
- Export citation
On the Steinhaus tiling problem
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 253-280
-
- Article
- Export citation
Intersection bodies and polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-34
-
- Article
- Export citation
The behaviour of the Riemann zeta-function on the critical line
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 281-313
-
- Article
- Export citation
A further generalization of Hilbert's inequality
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 35-39
-
- Article
- Export citation
Estimates of the least prime factor of a binomial coefficient
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-55
-
- Article
- Export citation
Lower bounds for multilinear forms defined on Hilbert Spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 315-322
-
- Article
- Export citation
On smooth gaps between consecutive prime numbers
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-75
-
- Article
- Export citation
Continuous functions on products of compact Hausdorff spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 323-330
-
- Article
- Export citation
Compact measure spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 331-336
-
- Article
- Export citation
A Bernstein-type theorem in hyperbolic spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-81
-
- Article
- Export citation
A generalized fundamental principle
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-92
-
- Article
- Export citation
On the convergence of Σ∞n = 1f(nx) for measurable functions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 337-341
-
- Article
- Export citation
Locally uniformly rotund norms
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 343-358
-
- Article
- Export citation
Flatness properties of acts over commutative, cancellative monoids
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-102
-
- Article
- Export citation
Asymptotic approximation of smooth convex bodies by general polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-125
-
- Article
- Export citation
On some questions of Erdős and Graham about Egyptian fractions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 359-372
-
- Article
- Export citation

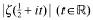 between successive zeros. Our results are to be independent of any unproved hypothesis. Put
between successive zeros. Our results are to be independent of any unproved hypothesis. Put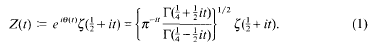
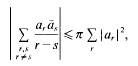
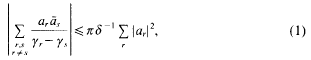

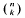 are >
are >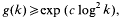
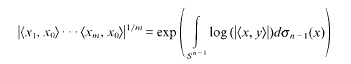
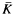 of
of