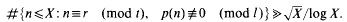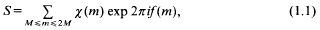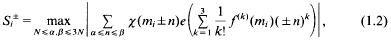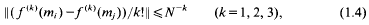Research Article
Isotropic surface area measures
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-13
-
- Article
- Export citation
Convex intersection bodies in three and four dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 15-27
-
- Article
- Export citation
Intersection bodies and polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 29-34
-
- Article
- Export citation
A further generalization of Hilbert's inequality
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 35-39
-
- Article
- Export citation
Estimates of the least prime factor of a binomial coefficient
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-55
-
- Article
- Export citation
On smooth gaps between consecutive prime numbers
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-75
-
- Article
- Export citation
A Bernstein-type theorem in hyperbolic spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 77-81
-
- Article
- Export citation
A generalized fundamental principle
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-92
-
- Article
- Export citation
Flatness properties of acts over commutative, cancellative monoids
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-102
-
- Article
- Export citation
Asymptotic approximation of smooth convex bodies by general polytopes
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 103-125
-
- Article
- Export citation
Convex bodies with non-convex cross-section bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-129
-
- Article
- Export citation
Maximal hyperplane sections of convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-136
-
- Article
- Export citation
A density bound for efficient packings of 3-space with centrally symmetric convex bodies
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-144
-
- Article
- Export citation
On the location of spectral concentration for perturbed discrete spectra
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-154
-
- Article
- Export citation
Uniqueness of solutions to certain hyperbolic boundary value problems in a semi-infinite strip
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-163
-
- Article
- Export citation
Kahane-Khinchine type inequalities for negative exponent
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 165-173
-
- Article
- Export citation
Rings which are residually ℤ
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 175-183
-
- Article
- Export citation
Non-vanishing of the partition function modulo odd primes l
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 185-192
-
- Article
- Export citation
On similar short sums
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-204
-
- Article
- Export citation
On congruence compact monoids
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-224
-
- Article
- Export citation

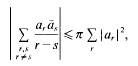
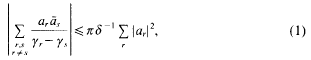

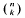 are >
are >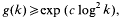
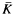 of
of 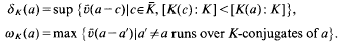
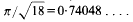
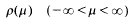
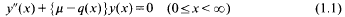

 be a class of structures for a first-order language and let
be a class of structures for a first-order language and let