Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T05:13:58.205Z Has data issue: false hasContentIssue false
  • English
  • Français

On the location of spectral concentration for perturbed discrete spectra

Part of: Ordinary differential operators

Published online by Cambridge University Press:  26 February 2010

M. S. P. Eastham
M. S. P. Eastham
Affiliation:
Department of Computer Science, Cardiff University of Wales, P.O. Box 916, Cardiff CF24 3XF
Get access

Extract

We consider the spectral function

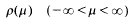
associated with the Sturm-Liouville equation

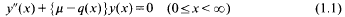
in situations where q(x) →−∞ as x → ∞ and (1.1) is in the Weyl limit-point case at ∞. As usual, q is real-valued and locally integrable in [0, ∞], and our particular concern is where q(x) has the form

where c (>0) is a parameter, s and p are non-negative on [0, ∞], p(x) → ∞ and p(x) = 0{s(x) } as x → ∞. As the boundary condition at x = 0, we take the Dirichlet condition y(0) = 0 for convenience: we can equally take the Neumann condition y′ (0) = 0 or generally a1y(0) + a2y′ (0) = 0 with real a1 and a2.

MSC classification

Secondary: 34L99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 46 , Issue 1 , June 1999 , pp. 145 - 154
Copyright
Copyright © University College London 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Ahia, F.. Lower bounds on width of Stark resonances in one dimension. Letters in Math. Phys., 24 (1992), 21–29.CrossRefGoogle Scholar
2.Brown, B. M., Eastham, M. S. P. and McCormack, D. K. R.. Spectral concentration and rapidly decaying potentials. J. Comp. Appl. Math., 81 (1997), 333–348.CrossRefGoogle Scholar
3.Brown, B. M., Eastham, M. S. P. and McCormack, D. K. R.. Spectral concentration and perturbed discrete spectra. J. Comp. Appl. Math., 86 (1997), 415–425.CrossRefGoogle Scholar
4.Eastham, M. S. P.. The asymptotic form of the spectral function in Sturm-Liouville problems with a large potential like -xc (c≤2). Proc. Roy. Soc. Edinburgh, 128A (1998), 37–45.CrossRefGoogle Scholar
5.Eastham, M. S. P.. On the location of spectral concentration for Sturm-Liouville problems with rapidly decaying potehtial. Mathematika, 45 (1998), 25–36.CrossRefGoogle Scholar
6.Harrell, E. and Simon, B.. The mathematical theory of resonances whose widths are exponentially small. Duke Math. J., 47 (1980), 845–902.CrossRefGoogle Scholar
7.Hinton, D. B. and Shaw, J. K.. Spectral concentration for Hamiltonian systems. Helvetica Phys. Ada, 58 (1985), 982–994.Google Scholar
8.Hislop, P. D. and Sigal, I. M.. Introduction to Spectral Theory (Springer, 1996).CrossRefGoogle Scholar
9.Hunziker, W.. Notes on asymptotic perturbation theory for Schrodinger eigenvalue problems. Helvetica Phys. Ada, 61 (1988), 257–304.Google Scholar
10.Marietta, M., The detection of quantum-mechanical resonances using the Pruess method. Technical Note ACM 90-14, Royal Military College of Science, 1990.Google Scholar
11.McLeod, J. B.. Spectral concentration I: the one-dimensional Schrödinger operator. Perturbation Theory and its Applications in Quantum Mechanics, Wilcox, C. H. editor (Wiley, 1966).Google Scholar
12.Reed, M. and Simon, B.. Methods of Modern Mathematical Physics, Vol. 4: Analysis of Operators (Academic Press, 1978).Google Scholar
13.Stolz, G.. Bounded solutions and absolute continuity of Sturm-Liouville operators. J. Math. Anal. Appl., 169 (1992), 210–228.CrossRefGoogle Scholar
14.Titchmarsh, E. C.. Eigenfunction Expansions, Part I, 2nd ed. (Clarendon Press, Oxford, 1962).Google Scholar
15.Titchmarsh, E. C.. Eigenfunction Expansions, Part II (Clarendon Press, Oxford, 1958).Google Scholar