Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T12:12:09.764Z Has data issue: false hasContentIssue false
  • English
  • Français

L-Series for genera at s = 1

Published online by Cambridge University Press:  26 February 2010

Kenneth H. Rosen
Kenneth H. Rosen
Affiliation:
Department of Mathematics, The University of Maine, Orono, Maine 04469, U.S.A.
Get access

Abstract

It has been conjectured that, if p ≡ 1 (mod 4) is prime, and if d < 0 is a square-free discriminant with 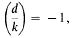then

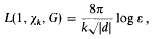
Where 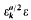belongs to the field 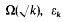is the fundamental unit of Q(√k), 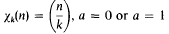depending on whether there are an even number or an odd number of classes per genus in Q(√d), and Ω is the genus field of Q(√d). Here 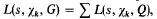the summation being over a complete set of inequivalent forms in the genus G, and

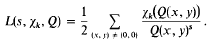
In this paper it will be shown that this conjecture is true when d is the product of two odd discriminants. An example when d is the product of three prime discriminants is discussed.

Type
Research Article
Information
Mathematika , Volume 27 , Issue 1 , June 1980 , pp. 10 - 16
Copyright
Copyright © University College London 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Brown, E.. “Binary quadratic forms of determinant – pq”, J. Number Theory, 4 (1972), 408–410.CrossRefGoogle Scholar
2.Brown, E.. “Class numbers of real quadratic fields”, Trans. Amer. Math. Soc., 190 (1974), 99–107.CrossRefGoogle Scholar
3.Brown, E. and Parry, C.. “Class numbers of quadratic fields having exactly three discriminantal divisors”, J. reine angew. Math., 260 (1970), 31–34.Google Scholar
4.Hasse, H.. “Imaginàr-quadratische Zahlkörpers mit zwei Diskriminantenprimteilern”, J. reine angew. Math., 241 (1970), 1–6.Google Scholar
5.Ince, E. L.. “Cycles of reduced ideals in quadratic fields”, Mathematical Tables, Vol. IV (British Association for the Advancement of Science, London, 1934).Google Scholar
6.Kenku, M.. “On the L-functions for quadratic forms”, J. reine angew. Math., 276 (1975), 36–43.Google Scholar
7.Möller, M.. Tabelle der nach Klassenzahler geordneten Grundzahlen imaginàr-quadratischer Zahlkörper (Bonn, 1972).Google Scholar
8.Rédei, L.. “Arithmetischer Beweis des Satzes über die Anzahl der durch Vier teilbaren Invarianten der absoluten Klassengruppe im quadratischen Zahlkörper”, J. reine angew. Math., 171 (1934), 55–60.CrossRefGoogle Scholar
9.Rédei, L.. “Ein neues zahlentheoretisches Symbol mit Anwendung auf die Theorie der quadratischer Zahlkörper I”, J. reine angew. Math., 180 (1939), 1–43.CrossRefGoogle Scholar
10.Rédei, L.. “Über die Grundeinheit und die durch 8 teilbaren Invarianten der absoluten Klassengruppe im quadratischen Zahlkörper”, J. reine angew. Math., 171 (1934), 131–148.CrossRefGoogle Scholar
11.Rédei, L. and Reichardt, H.. “Die Anzahl der durch 4 teilbaren Invarianten der Klassengruppe eines beliebigen quadratischen Zahlkörpers”, J. reine angew. Math., 170 (1933), 69–74.Google Scholar
12.Rosen, K. H.. The Values of Certain L-Series at s = 1, Thesis (M.I.T., 1976).Google Scholar
13.Rosen, K. H.. “L-Series for Quadratic Forms, I, and II”, Amer. J. Math. (to appear).Google Scholar
14.Schertz, R.. “L-Reihen in imaginàr-quadratischen Zahlkörpern und ihre Anwendung auf Klassenzahlprobleme bei quadratischen und biquadratischen Zahlkörpern, I, II”, J. reine angew. Math., 262/3 (1973), 120–133 and 270 (1974), 195–212.Google Scholar
15.Scholz, A.. “Über die Losbarkeit der Gleichung t2-Du2 = -4”, Math. Z., 39 (1934), 95–111.CrossRefGoogle Scholar
16.Stark, H. M.. “L-functions and character sums for quadratic forms, I, II”, Ada, Arith., 14 (1968), 35–50 and 15 (1969), 307–317.CrossRefGoogle Scholar
17.Stark, H. M.. “A transcendence theorem for class-number problems”, Ann. of Math., 94 (1971), 153–173.CrossRefGoogle Scholar
18.Stark, H. M.. “Values of L-functions at s = 1,1. L-functions for quadratic forms”, Advances in Math., 7 (1971), 301–343.CrossRefGoogle Scholar
19.Wada, H.. “On the class number and the unit group of certain algebraic number fields”, J. Fac. Sci. Univ. Tokyo, Sec. I, 13 (1966), 201–209.Google Scholar