Research Article
On the chromatic number of binary matroids
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-9
-
- Article
- Export citation
On a theorem of Bombieri–Vinogradov type
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-152
-
- Article
- Export citation
L-Series for genera at s = 1
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-16
-
- Article
- Export citation
On irregularities of distribution
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-170
-
- Article
- Export citation
Locally minimal Epstein zeta functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
-
- Article
- Export citation
On the number of square-full integers between successive squares
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-178
-
- Article
- Export citation
On the unsolvability of some Diophantine equations of a modified Fermat type
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 179-187
-
- Article
- Export citation
Small fractional parts of quadratic forms in many variables
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-29
-
- Article
- Export citation
Small solutions of quadratic and quartic congruences
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 30-45
-
- Article
- Export citation
Determination of a binary quadratic form by its values at integer points: Acknowledgement
-
- Published online by Cambridge University Press:
- 26 February 2010, p. 188
-
- Article
- Export citation
Rarefaction indices
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 46-57
-
- Article
- Export citation
The inefficiency of certain periodic processes in linear thermoelasticity
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-196
-
- Article
- Export citation
Some remarks on fibrations of monoids and their classifying spaces
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-212
-
- Article
- Export citation
Shadow-boundaries and cuts of convex polytopes
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-63
-
- Article
- Export citation
A graph and its complement with specified properties V: The self-complement index
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 64-68
-
- Article
- Export citation
Countable partitions of product spaces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-224
-
- Article
- Export citation
Proof of D. J. Newman's coprime mapping conjecture
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-83
-
- Article
- Export citation
Measures on totally ordered spaces
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 225-235
-
- Article
- Export citation
Popular values of Euler's function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 84-89
-
- Article
- Export citation
Borel isomorphisms at the first level: Corrigenda et addenda
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 236-260
-
- Article
- Export citation

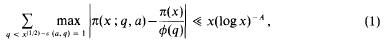
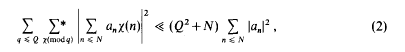
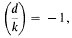 then
then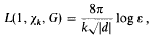
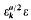 belongs to the field
belongs to the field 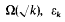 is the fundamental unit of
is the fundamental unit of 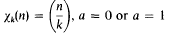 depending on whether there are an even number or an odd number of classes per genus in
depending on whether there are an even number or an odd number of classes per genus in 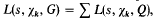 the summation being over a complete set of inequivalent forms in the genus
the summation being over a complete set of inequivalent forms in the genus 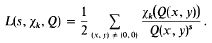
 of
of 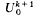 , where, for
, where, for 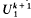 , let
, let 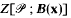 denote the number of points of
denote the number of points of 
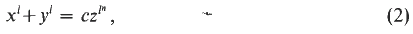
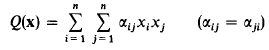
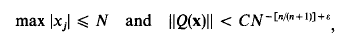
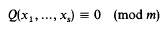
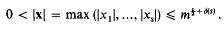

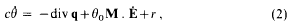
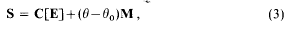

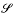 of
of