What should a generic object be?

Abstract

Jacobs has proposed definitions for (weak, strong, split) generic objects for a fibered category; building on his definition of (split) generic objects, Jacobs develops a menagerie of important fibrational structures with applications to categorical logic and computer science, including higher order fibrations, polymorphic fibrations, $\lambda2$ -fibrations, triposes, and others. We observe that a split generic object need not in particular be a generic object under the given definitions, and that the definitions of polymorphic fibrations, triposes, etc. are strict enough to rule out some fundamental examples: for instance, the fibered preorder induced by a partial combinatory algebra in realizability is not a tripos in this sense. We propose a new alignment of terminology that emphasizes the forms of generic object appearing most commonly in nature, i.e. in the study of internal categories, triposes, and the denotational semantics of polymorphism. In addition, we propose a new class of acyclic generic objects inspired by recent developments in higher category theory and the semantics of homotopy type theory, generalizing the realignment property of universes to the setting of an arbitrary fibration.

1. Introduction

Since the latter half of the 20th century, fibered category theory or the theory of fibrations has played an important background role in both the applications and foundations of category theory (Bénabou 1985; Grothendieck 1971). Fibered categories, also known as fibrations, are a formalism for manipulating categories that are defined relative to another category, generalizing the way that ordinary categories can be thought of as being defined relative to the category of sets.

The sense in which ordinary category theory is pinned to the category of sets can be illustrated by considering the definition of when a category ${\mathscr{C}}$ “has products”:

Definition 1. A category ${\mathscr{C}}$ has products when for any indexed family $\{{E_i\in {\mathscr{C}}}\}_{i\in I}$ of objects, there exists an object $\prod_{i\in I}{E_i}\in{\mathscr{C}}$ together with a family of morphisms $p_k:{\prod_{i\in I}E_i}\longrightarrow{E_k}$ such that for any family of morphisms $h_k:{H}\longrightarrow{E_k}$ there exists a unique morphism $h:{H}\longrightarrow{\prod_{i\in I}E_i}$ factoring each $h_k$ through $p_k$ .

In the above, the dependency on the category $\textbf{Set}$ is clear: the indexing object I is a set. If we had required I to be drawn from a proper subcategory of $\textbf{Set}$ (e.g. finite sets) or a proper supercategory (e.g. classes), the notion of product defined thereby would have been different. The purpose of the formalism of fibered categories is to explicitly control the ambient category that parameterizes all indexed notions, such as products, sums, limits, colimits, etc.

Remark 2 (Relevance to computer science). The ability to explicitly control the parameterization of products and sums is very important in theoretical computer science, especially for the denotational semantics of polymorphic types of the form $\forall\alpha. \tau[{\alpha}]$ . Such a polymorphic type should be understood as the product of all $\tau[{\alpha}]$ indexed in the “set” of all types, but a famous result of Freyd (2003) shows that if a category ${\mathscr{C}}$ has products of this form parameterized in $\textbf{Set}$ , then ${\mathscr{C}}$ must be a preorder. Far from bringing to an early end the study of polymorphic types in computer science, awareness of Freyd’s result sparked and guided the search for ambient categories other than $\textbf{Set}$ in which to parameterize these products (Hyland 1988; Hyland et al. 1990; Pitts 1987). Fibered category theory provides the optimal language to understand all such indexing scenarios, and the textbook of Jacobs (1999), discussed at length in the present paper, provides a detailed introduction to the applications of fibered category theory to theoretical computer science.

1.1 Introduction to fibered categories

Before giving a general definition, we will see the way that fibered categorical language indeed makes parameterization explicit by considering the prototype of all fibered categories, the category ${\textbf{Fam}}({{\mathscr{C}}})$ of $\textbf{Set}$ -indexed families of objects of a category ${\mathscr{C}}$ .

Construction 3 (The category of families) We define ${\textbf{Fam}}({{\mathscr{C}}})$ to be the category of $\textbf{Set}$ -indexed families in ${\mathscr{C}}$ , such that

1. (1) an object of ${\textbf{Fam}}({{\mathscr{C}}})$ is a family $\{{E_i\in{\mathscr{C}}}\}_{i\in I}$ where I is a set,

2. (2) a morphism ${\{{E_i}\}_{i \in I}}\longrightarrow{\{{F_j}\}_{j\in J}}$ in ${\textbf{Fam}}({{\mathscr{C}}})$ is given by a function $u:{I}\longrightarrow{J}$ together with for each $i\in I$ a morphism $\bar{u}_i:{E_i}\longrightarrow{F_{ui}}$ .

There is an evident functor $p:{{\textbf{Fam}}({{\mathscr{C}}})}\longrightarrow{\textbf{Set}}$ taking $({\{{E_i}\}_{i\in I}})$ to I.

Construction 4 (Fiber categories). For each $I\in \textbf{Set}$ , we may define the fiber ${\textbf{Fam}}({{\mathscr{C}}})_I$ of ${\textbf{Fam}}({{\mathscr{C}}})$ over I to be the category of I-indexed families $\{{E_i\in {\mathscr{C}}}\}_{i\in I}$ in ${\mathscr{C}}$ , with morphisms ${\{{F_i}\}_{i\in I}}\longrightarrow{\{{E_i}\}_{i\in I}}$ given by morphisms $h_i:{F_i}\longrightarrow{E_i}$ for each $i\in I$ .

More abstractly, the fiber category ${\textbf{Fam}}({{\mathscr{C}}})_I$ is the following pullback:

Construction 5 (Reindexing functors). For any function $u:{J}\longrightarrow{I}$ , there is a corresponding reindexing functor $u^*:{{\textbf{Fam}}({{\mathscr{C}}})_I}\longrightarrow{{\textbf{Fam}}({{\mathscr{C}}})_J}$ that restricts an I-indexed family into a J-indexed family by precomposition.

With the reindexing functors in hand, can now rephrase the condition that ${\mathscr{C}}$ has products (Definition 1) in terms of ${\textbf{Fam}}({{\mathscr{C}}})$ .

Proposition 6. A category ${\mathscr{C}}$ has products if and only if for each product projection function $\pi_{I,J}:{I\times J}\longrightarrow{I}$ , the reindexing functor $\pi_{I,J}:{{\textbf{Fam}}({{\mathscr{C}}})_{I}}\longrightarrow{{\textbf{Fam}}({{\mathscr{C}}})_{I\times J}}$ has a right adjoint $\prod_{({I,J})}:{{\textbf{Fam}}({{\mathscr{C}}})_{I\times J}}\longrightarrow{{\textbf{Fam}}({{\mathscr{C}}})_I}$ such that the following Beck–Chevalley condition holds: for any function $u:{K}\longrightarrow{I}$ , the canonical natural transformation ${u^*\circ \prod_{({I,J})}}\longrightarrow{\prod_{({K,J})}\circ [{u\times \mathsf{id}_J}]^*}$ is an isomorphism.

The characterization of products in terms of the category of families may seem more complicated, but it has a remarkable advantage: we can replace ${{\textbf{Fam}}({{\mathscr{C}}})}\longrightarrow{\textbf{Set}}$ with a different functor satisfying similar properties in order to speak more generally of when one category has “products” that are parameterized in another category. The properties that this functor has to satisfy for the notion to make sense are embodied in the definition of a fibration or fibered category; a functor ${\mathscr{E}}\longrightarrow{\mathscr{B}}$ will be called a fibration when it behaves similarly to the functor projecting the parameterizing object from a category of families of objects. We begin with an auxiliary definition of cartesian morphism:

Definition 7. Let $p:{{\mathscr{E}}}\longrightarrow{{\mathscr{B}}}$ and let ${E}\longrightarrow{F}$ be a morphism in ${\mathscr{E}}$ , which we depict as follows:

In the diagram above, we say that ${E}\longrightarrow{F}$ lies over ${pE}\longrightarrow{pF}$ . We say that ${E}\longrightarrow{F}$ is cartesian in p when for any morphism ${H}\longrightarrow{F}$ in ${\mathscr{E}}$ and ${pH}\longrightarrow{pE}$ such that the former lies over the composite $pH\to pE\to pF$ in ${\mathscr{B}}$ , there exists a unique morphism ${H}\longrightarrow{E}$ lying over ${pH}\longrightarrow{pE}$ such that ${H}\longrightarrow{F}$ lies over the composite ${pH}\longrightarrow{pE}$ as depicted below:

Remark 8 (Explication of cartesian maps). Returning to our example of the category of families ${\textbf{Fam}}({{\mathscr{C}}})$ over $\textbf{Set}$ , we can make sense of the notion of a cartesian map. Given a function $u:{J}\longrightarrow{I}$ of indexing sets, the reindexing functor $u^*$ takes I-indexed families to J-indexed families. Given an I-indexed family $\{{E_i}\}_{i\in I}$ , we may define a morphism ${u^*\{{E_i}\}_{i\in I}}\longrightarrow{\{{E_i}\}_{i\in I}}$ in ${\mathscr{C}}$ whose first component is $u:{J}\longrightarrow{I}$ and whose second component is the identity function ${E_{uj}}\longrightarrow{E_{uj}}$ at each $j\in J$ . The morphism ${u^*\{{E_i}\}_{i\in I}}\longrightarrow{\{{E_i}\}_{i\in I}}$ is then cartesian in $p:{{\textbf{Fam}}({{\mathscr{C}}})}\longrightarrow{\textbf{Set}}$ .

Exercise 9. Verify that the morphism ${u^*\{{E_i}\}_{i\in I}}\longrightarrow{\{{E_i}\}_{i\in I}}$ constructed in Remark 8 is indeed cartesian in $p:{{\textbf{Fam}}({{\mathscr{C}}})}\longrightarrow{\textbf{Set}}$ .

In fact, we can strengthen Exercise 9 to give an extrinsic characterization of cartesian morphisms in ${\textbf{Fam}}({{\mathscr{C}}})$ : cartesian morphisms are exactly the “fiberwise isomorphisms”.

Exercise 10 Let $E = \{{E_i}\}_{i\in I}$ and $F = \{{F_j}\}_{j\in J}$ be objects of ${\textbf{Fam}}({{\mathscr{C}}})$ , and let $f:{E}\longrightarrow{F}$ be a morphism between them. Show that the following are equivalent:

1. (1) the morphism $f:{E}\longrightarrow{F}$ is cartesian;

2. (2) for each $i\in I$ , the component $f_i:{E_i}\longrightarrow{F_{pfi}}$ is an isomorphism.

The name “cartesian morphism” is inspired by pullbacks, as we see in Exercise 11 below.

Exercise 11. Let ${\mathscr{B}}^{\to}$ be the arrow category of ${\mathscr{B}}$ , whose objects are morphisms of ${\mathscr{B}}$ and whose morphisms are commuting squares between them; let $\mathsf{cod}:{{\mathscr{B}}^{\to}}\longrightarrow{{\mathscr{B}}}$ be the codomain functor that projects the codomain of a map ${A}\longrightarrow{B}$ . Show that a morphism ${E}\longrightarrow{F}\in{\mathscr{B}}^{\to}$ is cartesian if and only if the corresponding square in ${\mathscr{B}}$ is a pullback square (also called a cartesian square).

The relationship between cartesian morphisms and pullback squares expressed by Exercise 11 suggests a generalization of the conventional “pullback corners” notation to an arbitrary fibration, which we shall use liberally.

Convention 12 (Generalized “pullback corners”). Let $p:{{\mathscr{E}}}\longrightarrow{{\mathscr{B}}}$ be a functor; when we wish to indicate that a morphism ${E}\longrightarrow{F}$ in ${\mathscr{E}}$ is cartesian over ${pE}\longrightarrow{pF}$ , we will display it using a “pullback corner” notation as follows:

Finally, we may give the definition of a fibration.

Definition 13. A functor $p:{{\mathscr{E}}}\longrightarrow{{\mathscr{B}}}$ is called a fibration when for any object $E\in {\mathscr{E}}$ and morphism ${B}\longrightarrow{pE} \in {\mathscr{B}}$ there exists a cartesian morphism ${H}\longrightarrow{E}$ lying over ${B}\longrightarrow{pE}$ . The cartesian morphism is often called the cartesian lift of ${B}\longrightarrow{pE}$ at E.

Convention 14. We will depict a fibration

using triangular arrows. When we wish to leave the functor implicit, we refer to ${\mathscr{E}}$ as a fibered category over ${\mathscr{B}}$ . In the same way that one writes $A\times B$ for the apex of a product diagram, we will often write $\bar{u}:{u^*E}\longrightarrow{E}$ for the cartesian lift of $u:{B}\longrightarrow{pE}$ at E as depicted below:

In the case of ${\textbf{Fam}}{{\mathscr{E}}}$ , the existence of cartesian lifts for each $u:{B}\longrightarrow{pE}$ corresponds to the reindexing functors $u^*:{{\textbf{Fam}}({{\mathscr{C}}})_{pE}}\longrightarrow{{\textbf{Fam}}({{\mathscr{C}}})_{B}}$ .

Exercise 15. Verify that the functor is a fibration.

Exercise 16. Conclude from Exercise 11 that the codomain functor ${{\mathscr{B}}^{\to}}\longrightarrow{{\mathscr{B}}}$ is a fibration if and only if ${\mathscr{B}}$ has all pullbacks.

When the codomain functor ${{\mathscr{B}}^{\to}}\longrightarrow{{\mathscr{B}}}$ is a fibration, we will refer to it as the fundamental fibration, written $\textbf{P}_{{\mathscr{B}}}$ following Streicher (2021).

1.1.1 Small categories, internal categories

An ordinary category need not have a set of objects – for instance, the category $\textbf{Set}$ of all sets has a proper class of objects.¹ Likewise, it is possible to find categories such that between two objects there may be a proper class of morphisms (e.g. the category of sets and isomorphism classes of spans between them). A category that has hom sets is called locally small, and we will refer to a category that has, up to equivalence, a set of objects as globally small. A category that has both these properties is equivalent to a small category in the ordinary sense. Small categories are very useful: for instance, if $\mathbb{C}$ is a small category then the category of functors $[{\mathbb{C},\textbf{Set}}]$ is a Grothendieck topos. Functor categories of this kind play an important role in theoretical computer science (e.g. Birkedal et al. 2011; Oles 1986; Reynolds 1995).

The idea of a (globally, locally) small category can be relativized from $\textbf{Set}$ to another category in two a priori different ways that ultimately coincide up to equivalence. The simplest and more naïve way to think of a small category $\mathbb{C}$ in a category ${\mathscr{B}}$ is as an algebra for the sorts and operations of the theory of a category internal to ${\mathscr{B}}$ , which we develop below; the more sophisticated way is to view $\mathbb{C}$ as a fibration over ${\mathscr{B}}$ satisfying a generalization of the global and local smallness conditions.

Definition 17. Let ${\mathscr{B}}$ be a category that has pullbacks. An internal category or category object in ${\mathscr{B}}$ is given by:

1. (1) an object $\mathbb{C}_0\in{\mathscr{B}}$ of objects,

2. (2) and an object $\mathbb{C}_1\in{\mathscr{B}}$ of morphisms,

3. (3) and source and target maps $s,t:{\mathbb{C}_1}\longrightarrow{\mathbb{C}_0}$ ,

4. (4) and a morphism $i:{\mathbb{C}_0}\longrightarrow{\mathbb{C}_1}$ choosing the identity maps, such that $s\circ i = \mathsf{id}_{\mathbb{C}_0} = t\circ i$ ,

5. (5) and a morphism $c:{\mathbb{C}_1\times_{\mathbb{C}_0}\mathbb{C}_1}\longrightarrow{\mathbb{C}_1}$ choosing composite maps such that $s\circ c = s\circ \pi_1$ and $t\circ c = t\circ \pi_2$ ,

6. (6) (plus associativity and unit laws for composition and identity)

Observation 18. When ${\mathscr{B}} = \textbf{Set}$ we obtain exactly the ordinary notion of a small category, i.e. a small category is the same thing as an internal category or category object in $\textbf{Set}$ .

In the previous section, we have argued that fibrations are a fruitful way to think about categories defined relative to another category. Indeed, we may view an internal category $\mathbb{C}$ as a fibration via a process called externalization. This proceeds in two steps; first we construct a presheaf of categories on ${\mathscr{B}}$ , and then we use the Grothendieck construction to turn it into a fibration.

Construction 19 (The presheaf of categories associated to an internal category) construction]con:icat-to-psh Let $\mathbb{C}$ be an internal category in ${\mathscr{B}}$ . We may define a presheaf of categories $\mathbb{C}^\bullet:{{{\mathscr{B}}}^{\mathsf{op}}}\longrightarrow{\textbf{Cat}}$ like so:

1. (1) for $I\in{\mathscr{B}}$ , an object of $\mathbb{C}^I$ is given by a morphism $\alpha:{I}\longrightarrow{\mathbb{C}_0}$ ,

2. (2) for $I\in{\mathscr{B}}$ , a morphism ${\alpha}\longrightarrow{\beta}\in\mathbb{C}^I$ is given by a morphism $h:{I}\longrightarrow{\mathbb{C}_1}$ such that $s\circ h = \alpha$ and $t\circ h = \beta$ ,

3. (3) for $u:{J}\longrightarrow{I}$ in ${\mathscr{B}}$ , the reindexing $u^*:{\mathbb{C}^I}\longrightarrow{\mathbb{C}^J}$ is given on both objects and morphisms by precomposition with u.

Construction 20 (The Grothendieck construction). Let $\mathbb{C}^\bullet:{{{\mathscr{B}}}^{\mathsf{op}}}\longrightarrow{\textbf{Cat}}$ be a presheaf of categories; we define its total category $\int_{{\mathscr{B}}}\!\mathbb{C}^\bullet$ as follows:

1. (1) an object of $\int_{{\mathscr{B}}}\!\mathbb{C}^\bullet$ is given by a pair of an object $I\in{\mathscr{B}}$ and an object $c\in \mathbb{C}^I$ ,

2. (2) a morphism ${[{J,c}]}\longrightarrow{[{I,d}]}$ is given by a pair of a morphism $u:{J}\longrightarrow{I}\in{\mathscr{B}}$ and a morphism ${c}\longrightarrow{\mathbb{C}^ud}$ in $\mathbb{C}^J$ .

There is an evident functor $p:{\int_{{\mathscr{B}}}\!\mathbb{C}^\bullet}\longrightarrow{{\mathscr{B}}}$ ; it is this functor that is referred to as the Grothendieck construction.

Exercise 21. Verify that the Grothendieck construction of any presheaf of categories $\mathbb{C}^\bullet:{{{\mathscr{B}}}^{\mathsf{op}}}\longrightarrow{\textbf{Cat}}$ is a fibration.

Observe that the presheaf of categories associated to an internal category is, in each fiber I, the category object in $\textbf{Set}$ obtained by restricting along the functor $I:{\textbf{1}}\longrightarrow{{\mathscr{B}}}$ .

Definition 22 (Externalization of an internal category) Let $\mathbb{C}$ be an internal category in ${\mathscr{B}}$ ; its externalization is defined to be the Grothendieck construction of the associated presheaf of categories (Construction 19).

Remark 23. When $\mathbb{C}$ is an internal category in $\textbf{Set}$ , the externalization $[\mathbb{C}]$ is the family fibration ${\textbf{Fam}}{\mathbb{C}}$ described Construction 3.

As promised we may now isolate the properties of the fibered category $[\mathbb{C}]$ that correspond (up to equivalence) to arising by externalization from an internal category.

Definition 24. A fibered category is called globally small if there is an object $T\in{\mathscr{E}}$ such that for any $X\in{\mathscr{E}}$ there exists a (not necessarily unique) cartesian map ${X}\longrightarrow{T}$ .

The property of global smallness described above is often phrased as having a “generic object” $T\in{\mathscr{E}}$ , but the reason for this paper’s existence is that the precise definition of “generic” means in this context is somewhat controversial, and the bulk of the present paper is devoted to justifying the precise meaning for genericity that we have chosen (in agreement with Definition 24). Note that our Definition 24 does not agree with that of Jacobs (1999), who assumes additional (somewhat rare) properties of the object T, namely that for $X\in{\mathscr{E}}$ there is exactly one morphism ${pX}\longrightarrow{pT}$ lying underneath a cartesian morphism ${X}\longrightarrow{T}$ . We will show Section 3.1 that ours is the correct definition.

Definition 25 (Bénabou 1975; Streicher 2021). A fibered category

is called locally small when for any $I\in {\mathscr{B}}$ and $X,Y\in{\mathscr{E}}_I$ there exists a span $X\xleftarrow{f} H \xrightarrow{g} Y$ with $f:{H}\longrightarrow{X}$ cartesian over $pg:{H}\longrightarrow{Y}$ as depicted below,

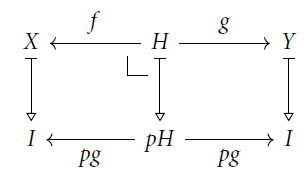
such that for any other span $X\xleftarrow{f'} K \xrightarrow{g'} Y$ where $f':{K}\longrightarrow{X}$ is cartesian over $pg':{pK}\longrightarrow{pY}$ , there is a unique map ${K}\longrightarrow{H}$ making the the following diagram commute:

Exercise 26 (Intermediate) Let ${\mathscr{C}}$ be an ordinary category show that the fibered category is locally small if and only if ${\mathscr{C}}$ is locally small. Show that ${\mathscr{C}}$ is equivalent to a small category if and only if is both globally small and locally small.

One of the fundamental results of fibered category theory is that, up to equivalence, global and local smallness in the sense of Definitions 24 and 25 suffice to detect internal categories, which we recall from Bénabou (1975):

Proposition 27 (Théorème 2, Bénabou 1975). A fibration is equivalent to the externalization of an internal category $\mathbb{E}$ if and only if it is both globally and locally small.

Although we do not include the (standard) proof of Proposition 27, it is instructive to understand the object $T\in[{\mathbb{E}}]$ in the externalization of an internal category $\mathbb{E}$ that renders $[{\mathbb{E}}]$ globally small. Recalling the definition of the externalization via the Grothendieck construction, we define the weak generic object T to be the pair $({\mathbb{E}_0,\mathsf{id}_{\mathbb{E}_0}:{\mathbb{E}_0}\longrightarrow{\mathbb{E}_0}})$ given by the object of objects and its identity map.

Example 28. When $\mathbb{E}$ is a small category, then the weak generic object of $[{\mathbb{E}}]={\textbf{Fam}}{\mathbb{E}}$ can be written as the family $\{{E}\}_{E\in \mathbb{E}_0}$ .

1.1.2 Cleavages and splittings

We briefly recall the definitions of cleavages and splittings for a fibration, as they are relevant to the rest of this paper.

Definition 29. A cleavage for a fibration is a choice $\mathfrak{r}$ of cartesian liftings, assigning to each morphism $u:{I}\longrightarrow{pX}\in {\mathscr{B}}$ in the base an object $\mathfrak{r}_u X\in {\mathscr{E}}$ over I and a cartesian morphism $\overline{\mathfrak{r}_u}:{\mathfrak{r}_u X}\longrightarrow{pX}$ over u.

The data of a cleavage $\mathfrak{r}$ extends for each $u:{I}\longrightarrow{J}\in {\mathscr{B}}$ to a reindexing functor $\mathfrak{r}_u:{{\mathscr{E}}^{J}}\longrightarrow{{\mathscr{E}}^{I}}$ .

Definition 30. A cleavage $\mathfrak{r}$ for a fibration is called split when the assignment of reindexing functors $u\mapsto \mathfrak{r}_u$ strictly preserves identities and compositions.

Convention 31. When the cleavage $\mathfrak{r}$ is understood, we will often write $u^*$ for $\mathfrak{r}_u$ .

A fibration equipped with a cleavage is called a cloven fibration; we may use the axiom of choice to equip any fibration with a (non-canonical) cleavage. When the cleavage associated to a cloven fibration is split, we speak of split fibrations. Observe that a splitting allows one to view a fibration as a presheaf of categories ${{{\mathscr{B}}}^{\mathsf{op}}}\longrightarrow{\textbf{Cat}}$ sending each $I\in{\mathscr{B}}$ to the fiber ${\mathscr{E}}^I$ . Recalling Construction 19, we see that the externalization of any internal category is split.

1.2 Goals and structure of this paper

Although the property stated in Definition 24, that there exist cartesian morphisms ${X}\longrightarrow{T}$ for any X, is the most that can be required for an arbitrary internal category, more restrictive notions of generic object have proved important in practice for different applications. Unfortunately, over the years a number of competing definitions have proliferated throughout the literature – and some of the more established of these definitions lead to false conclusions when taken too literally, as we point out in Section 3.1 in our discussion of Jacobs’ mistaken Corollary 9.5.6.

The goal of this paper, therefore, is to argue for a new alignment of terminology for the different forms of generic object that is both internally consistent and reflects the use of generic objects in practice. Because generic objects play an important role in several areas of application (categorical logic, algebraic set theory, homotopy type theory, denotational semantics of polymorphism, etc.), we believe that we have sufficient evidence today to correctly draw the map.

1. • In Section 2, we recall the definitions of several variants of generic object by Jacobs (1999); our main observation is that a split generic object in the sense of op. cit need not be a generic object in the same sense.

2. • In Section 3, we analyze the consequences of the definitions discussed in sec:kinds-of-generic-object for the use of generic objects in internal category theory, tripos theory, denotational semantics of polymorphism, algebraic set theory, and homotopy type theory.

3. • In sec:proposal, we propose new unified terminology and definitions for all extant forms of generic object (as well as one new one). Our proposal is summarized and compared with the literature in Table 1.

   Table 1. A Rosetta stone for the different terminologies for generic objects center

   

2. Four Kinds of Generic Object

We begin by recalling Definition 5.2.8 of Jacobs (1999), from which we omit some additional characterizations that will not play a role in our analysis.

Consider a fibration and an object T in the total category ${\mathscr{E}}$ . We call T a

1. (i) weak generic object if $ \forall X\in{\mathscr{E}}. \exists f:{X}\longrightarrow{T}. f\;{ is\;cartesian} $ .

2. (ii) generic object if $ \forall X\in{\mathscr{E}}. \exists! u:{pX}\longrightarrow{pT}. \exists f:{X}\longrightarrow{T}. f\;\textrm{is cartesian over}\;u $ .

3. (iii) strong generic object if $ \forall X\in{\mathscr{E}}. \exists! f:{X}\longrightarrow{T}. f\;{ is\;cartesian} $ .

Jacobs (1999) then defines split generic objects for split fibrations in Definition 5.2.1, paraphrased below:

A split fibration has a split generic object if there is an object $\Omega\in{\mathscr{B}}$ together with natural isomorphism $\theta:{{\mathscr{B}}({-,\Omega})}\longrightarrow{ \rm{ob} \,{{\mathscr{E}}_\bullet}}$ in $[{{{\mathscr{B}}}^{\mathsf{op}},\textbf{Set}}]$ , where the presheaf $\mathsf{ob}\,{\mathscr{E}}_\bullet$ is defined using the splitting.

A useful characterization of split generic objects is given in Lemma 5.2.2 of op. cit:

A split fibration has a split generic object if and only if there is an object $T\in{\mathscr{E}}$ with the property that $\forall X\in {\mathscr{E}}.\exists!u:{pX}\longrightarrow{pT}. u^*T = X$ . ( Jacobs 1999 )

Comment 32. The weak and strong generic objects of Jacobs (1999) are referred to by Phoa (1992) as generic objects and skeletal generic objects. Phoa (1992) does not consider the intermediate notion. On the other hand, Phoa (1992) defines strict generic objects relative to an arbitrary (non-split) cleavage; a split generic object is indeed a strict generic object in the sense of Phoa, but even for a split cleavage, a strict generic object need not be a split generic object. We will discuss Phoa’s terminology more in Comment 58.

2.1 Separating generic objects from strong generic objects

Jacobs (1999) notes that generic and strong generic objects coincide in fibered preorders, but they may differ otherwise – the difference emanating from the presence of non-trivial vertical automorphisms.

Example 33. Let G be a group containing two distinct elements $u\not= v$ , and let $\textbf{B}{G}$ be the groupoid with a single object whose hom set is G itself. The family fibration is a fibered category whose objects are just sets, but such that a morphism $f:{I}\longrightarrow{J}\in {\textbf{Fam}}{\textbf{B}{G}}$ is a pair (f,x) of a function $f:{I}\longrightarrow{J}\in \textbf{Set}$ together with a generalized element $x:{I}\longrightarrow{G}$ . Moreover, every morphism in ${\textbf{Fam}}{\textbf{B}{G}}$ is cartesian as $\textbf{B}{G}$ is a groupoid. The unique object $T\in {\textbf{Fam}}{\textbf{B}{G}}_{1_{\textbf{Set}}}$ is clearly generic, but not strong generic. Indeed, we have two distinct cartesian morphisms ${T}\longrightarrow{T}$ given by the pairs $({\mathsf{id}_{1_{\textbf{Set}}},u})\not=({\mathsf{id}_{1_{\textbf{Set}}},v})$ .

Example 34. Another class of examples comes from considering skeleta of full subcategories of $\textbf{Set}$ . For instance, one may take the skeleton of a Grothendieck universe and then externalize to obtain a fibration that has a generic object that is not strong.

2.2 A split generic object need not be a generic object

Construction 35 (The canonical splitting of the externalization) The externalization of an internal category is split in a canonical way: given $({I,c})\in [\mathbb{C}]$ and $u:{J}\longrightarrow{I}$ , we choose $u^*({I,c}) = ({J, c\circ u})$ . The cartesian morphism ${u^*({I,c})}\longrightarrow{({I,c})}$ is given by the pair $({u, \mathsf{id} \circ c\circ u})$ where $\mathsf{id}:{\mathbb{C}_0}\longrightarrow{\mathbb{C}_1}$ is the generic identity morphism.

Construction 36 (Weak, split generic objects in the externalization). The externalization has a weak generic object $T = ({\mathbb{C}_0, \mathsf{id}_{\mathbb{C}_0}})$ . Relative to the splitting of $[\mathbb{C}]$ from Construction 35, the weak generic object T is also a split generic object.

The weak generic object of the externalization of an internal category defined in Construction 36 obviously need not be a strong generic object, but it may be more surprising to learn that it also need not be a generic object at all. This can happen, for instance, when the internal category $\mathbb{C}$ has two distinct isomorphic objects; the following concrete example illustrates the problem.

Example 37 (A generic object that is not a object). Let U be a set of sets containing two distinct elements A,B with the same cardinality, and $\textbf{Set}_U\subseteq\textbf{Set}$ be the full subcategory of $\textbf{Set}$ spanned by U. Then, the family fibration has a split generic object T given by the pair $T=({U, \mathsf{id}_{U}})$ , but T is nonetheless not a generic object. Indeed, we have two cartesian morphisms ${({1_{\textbf{Set}}, A})}\longrightarrow{T}$ lying over distinct elements $A\not=B:{1_{\textbf{Set}}}\longrightarrow{U}$ , respectively.

Corollary 38. A split generic object is not necessarily a generic object.

2.3 Skeletal and gaunt small categories

We recall from Example 28 that for a small category $\mathbb{C}$ , the family fibration ${\textbf{Fam}}{\mathbb{C}}$ has a weak generic object $T =\{{C}\}_{C\in\mathbb{C}_0}$ . We will relate properties of the category $\mathbb{C}$ to corresponding properties of the weak generic object T.

Definition 39. A category is called skeletal when any to isomorphic objects are equal.

Definition 40. A category is called gaunt when any isomorphism in that category is the identity.

Comment 41 The term gaunt is used by Barwick and Schommer-Pries (2011), nLab (2021), Univalent Foundations Program (2013). In passing, Johnstone (2002) has referred to such categories as stiff.

Lemma 42. The category $\mathbb{C}$ is (respectively skeletal, gaunt) if and only if T is (respectively, generic, strong generic).

Proof. (1a) If $\mathbb{C}$ is skeletal, then T is generic; fix any family $\{{D_i}\}_{i\in I}$ and cartesian map $\chi:{\{{D_i}\}_{i\in I}}\longrightarrow{\{{C}\}_{{C\in\mathbb{C}}}}$ . By Exercise 10, $p\chi$ sends each $i\in I$ to an object $p\chi_i\in\mathbb{C}$ that is isomorphic to $D_i$ ; as $\mathbb{C}$ is skeletal, it follows that $p\chi_i = D_i$ and so we conclude that T is generic.

(1b) Assume conversely that T is generic and fix an isomorphism $f:D_0\cong D_1$ in $\mathbb{C}$ . We have two cartesian maps $h_0,h_1:{\{{D_0}\}}\longrightarrow{T}$ , with one lying over $D_0:{\{{*}\}}\longrightarrow{\mathbb{C}_0}$ via the identity morphism and the other lying over $D_1:{\{{*}\}}\longrightarrow{\mathbb{C}_0}$ via f. Since T is generic, these two cartesian maps must lie over the same element of $\mathbb{C}_0$ , so we have $D_0=D_1$ .

(2a) If $\mathbb{C}$ is gaunt, then T is strong generic; fix any two cartesian morphisms $h_0,h_1:{\{{D_i}\}_{i\in I}}\longrightarrow{\{{C}\}_{C\in\mathbb{C}}}$ . Because $\mathbb{C}$ is gaunt and thus skeletal, we know that $ph_0 = ph_1$ ; thus $h_0$ assigns to each $i\in I$ an isomorphism $h_{0,i}:{D_i}\longrightarrow{ph_1i}$ which is (by assumption) necessarily the identity. Thus, both $h_0$ and $h_1$ must send every $i\in I$ to the identity map on $D_i$ and are thus equal.

(2b) Conversely, we assume that T is strong generic to check that any isomorphism in $\mathbb{C}$ is an identity map; since T is necessarily also generic, it follows by the first case of the present lemma that we may consider just the automorphisms in $\mathbb{C}$ , considering Lemma 48. To show that any automorphism $f:D\cong D$ in $\mathbb{C}$ is the identity morphism, we proceed exactly as in the proof of Lemma 49 by observing that the two cartesian maps corresponding to the identity map and the automorphism f respectively are necessarily equal by our assumption that T is strong generic.

2.4 Generic objects from weak generic objects

Although the externalization of an internal category necessarily has a (split) weak generic object, in some cases it may also have a generic object T’ that embodies the skeleton of $\mathbb{C}$ as in Example 34, but T’ is usually different from the T.

Construction 43 (Computing the skeleton of a small category). Suppose that ${\mathscr{B}} = \textbf{Set}$ and thus $\mathbb{C}$ is an ordinary small category. Then we may consider the quotient $\mathbb{C}_0/\cong$ of the objects of $\mathbb{C}$ under isomorphism; in other words, this is the set of isomorphism classes of $\mathbb{C}$ -objects. Using the axiom of choice, we may arbitrarily choose a section $s:{\mathbb{C}_0/\cong}\longrightarrow{\mathbb{C}_0}$ to the quotient map; moreover, we may choose a function associating to each $u\in\mathbb{C}_0$ an isomorphism $u\cong s[{u}]_{/\cong}$ .

Lemma 44. The pair $T' = ({\mathbb{C}_0/\cong, s})$ is a generic object for ${\bf Fam}({\mathbb{C}})$ .

Proof. Fixing $({I,c})\in{\textbf{Fam}}{\mathbb{C}}$ we must choose a unique $u:{I}\longrightarrow{pT'}$ such that there exists a cartesian map ${({I,c})}\longrightarrow{T}$ lying over u. We choose $u({i}) = [{c({i})}]_{/\cong}$ , taking each index $i\in I$ to the isomorphism class of c(i).

1. (1) First of all, it is clear that there exists a cartesian map lying over u in the correct configuration.

2. (2) Fixing $v:{I}\longrightarrow{pT'}$ such that there exists a cartesian map ${({I,c})}\longrightarrow{T}$ lying over v, it remains to show that $v = u$ . This follows because such a cartesian map ensures that v and u are the same family of isomorphism classes of objects.

Lemma 45. If the T’ defined above is a split generic object, then $\mathbb{C}$ is skeletal.

Proof. We have already seen that T is a split generic object, hence if T’ is also split generic we have isomorphisms ${pT}\cong \mathbb{C}_0 \cong pT'$ and so we have $\mathbb{C}_0\cong \mathbb{C}_0/\cong$ .

We finally observe in Lemma 49 that if T’ is strong generic, then $\mathbb{C}$ is essentially gaunt in the sense defined below.

Definition 46. A category is called essentially gaunt when it is equivalent to a gaunt category.

Simon Henry has made the following observation:²

Observation 47. A category is essentially gaunt if and only if any automorphism in that category is the identity.

Lemma 48. A category is gaunt if and only if it is skeletal and essentially gaunt.

Proof. If $\mathbb{C}$ be gaunt, it is obviously both essentially gaunt and skeletal. Conversely, if $\mathbb{C}$ is essentially gaunt and skeletal, given any isomorphism $f:D\cong C$ we have $D=C$ and this f is an automorphism, which (by gauntness) is the identity.

Lemma 49. If T’ as defined above is a strong generic object, then $\mathbb{C}$ is essentially gaunt in the sense of Definition 46.

Proof. Let $f:{c}\longrightarrow{c}$ be an automorphism in $\mathbb{C}$ , i.e. a vertical isomorphism in ${\textbf{Fam}}{\mathbb{C}}_{1_{\textbf{Set}}}$ . Since T’ is strong generic, there exists a unique cartesian morphism ${({1_{\textbf{Set}},c})}\longrightarrow{T'}$ ; this means that there is a unique element $[{c}]\in \mathbb{C}_0/\cong$ and a unique isomorphism $h{c}\longrightarrow{s[{c}]}$ . Writing $\phi_c : c\cong s[{c}]$ for the (globally) chosen isomorphism, we have $f;\;\phi_c = h = \phi_c$ and hence $f = \mathsf{id}_{c}$ , so $\mathbb{C}$ is essentially gaunt.

Later on in Section 4, we will see that the original weak generic object T being strong generic corresponds to $\mathbb{C}$ being gaunt.

Thus, we conclude that although the family fibration ${\textbf{Fam}}{\mathbb{C}}$ over $\textbf{Set}$ of a small category $\mathbb{C}$ does have a generic object, this generic object cannot be either a split generic object or a strong generic object except in somewhat contrived scenarios.

2.5 Weak generic objects are the correct generalization of split generic objects

It is clear that any split generic object is in particular a weak generic object; but the converse also holds in a certain sense that we make precise below.

Construction 50 (Presheaf of categories). Let be a fibered category equipped with a cleavage $\mathfrak{r}$ , and let $T\in{\mathscr{E}}$ be a weak generic object for T. We may construct a presheaf of categories ${\mathscr{E}}^\bullet:{{{\mathscr{B}}}^{\mathsf{op}}}\longrightarrow{\textbf{Cat}}$ like so:

1. (1) an object of ${\mathscr{E}}^I$ is a morphism $\alpha:{I}\longrightarrow{pT}$ ,

2. (2) a morphism ${\alpha}\longrightarrow{\beta}$ in ${\mathscr{E}}^I$ is a vertical map $h:{\mathfrak{r}_\alpha T}\longrightarrow{\mathfrak{r}_\beta T}$ over I.

Construction 51. Let $\mathbb{E}:{{{\mathscr{B}}}^{\mathsf{op}}}\longrightarrow{\textbf{Cat}}$ be a presheaf of categories; then the Grothendieck construction has a splitting. Given $({J, \alpha})\in \int\!{\mathscr{E}}$ and $u:{I}\longrightarrow{J}$ , the object $u^*({J,\alpha})$ is chosen to be $({I, \alpha\circ u})$ and the cartesian morphism ${u^*({J,\alpha})}\longrightarrow{({J,\alpha})}$ over u in $\int\!{\mathscr{E}}^\bullet$ is defined to be the pair $({u, \mathsf{id}_{u^*\alpha}})$ .

Lemma 52. There is a fibered equivalence from $\int\!{\mathscr{E}}^\bullet$ to ${\mathscr{E}}$ over ${\mathscr{B}}$ .

Lemma 53. The pair $T' = ({T, \mathsf{id}_{T}})$ is a split generic object in .

Proof. Fixing $X\in \int\!{\mathscr{E}}^\bullet$ , we must check that there exists a unique $u:{pX}\longrightarrow{pT'}$ such that $u^*T' = X$ . Unfolding definitions, we fix $I\in {\mathscr{B}}$ and $\alpha:{I}\longrightarrow{T}$ to check that there is a unique $u:{I}\longrightarrow{T}$ such that $({I, u}) = ({I,\alpha})$ . Of course, this is true with $u=\alpha$ .

Thus, a weak generic object for a fibration generates in a canonical way a new equivalent split fibration that has a split generic object. This is the correspondence between weak generic and split generic objects.

3 Consequences for Internal Categories, Tripos Theory, Polymorphism, etc.

We recall several definitions from Jacobs (1999) below in order to illustrate a pattern.

1. (1) A higher order fibration is a first order fibration ³ with a generic object and a cartesian closed base category. Such a higher order fibration will be called split if the fibration is split and all of its fibered structure (including the generic object) is split. ( Jacobs 1999 , Definition 5.3.1)

2. (2) A tripos is a higher order fibration INSERT UNNUMBERED FIGURE HERESet over Set for which the induced products $\prod_{u}$ and coproducts $\coprod_{u}$ along an arbitrary function u satisfy the Beck–Chevalley condition. ( Jacobs 1999 , Definition 5.3.3)

3. (3) A polymorphic fibration is a fibration with a generic object, with fibered finite products and with finite products in its base category. It will be called split whenever all this structure is split. ( Jacobs 1999 , Definition 8.4.1).

4. (4) A polymorphic fibration with $\Omega$ in the base as a generic object will be called

   1. (a) a $\boldsymbol\lambda{\to}$ -fibration if it has fibered exponents;

   2. (b) a $\boldsymbol\lambda \boldsymbol{2}$ -fibration if it has fibered exponents and also simple $\Omega$ -products and coproducts;

   3. (c) a $\boldsymbol\lambda\boldsymbol\omega$ -fibration if it has fibered exponents, simple products, and coproducts, and exponents in its base category. (Jacobs 1999, Definition 8.4.3)

5. (5) Let $\Diamond$ be ${\to},2,\omega$ . A $\lambda\Diamond$ -fibration will be called split if all of its structure is split. In particular, its underlying polymorphic fibration is split. ( Jacobs 1999 , Definition 8.4.4)

A split generic object need not be a generic object as we have seen in Section 2.2, and indeed, is only quite rarely one. Consequently, a split polymorphic fibration is not the same thing as a split fibration with a split generic object and split fibered finite products. This disorder suggests that a change of definitions is in order, which we propose in Section 4.

3.1 Consequences for internal category theory

The somewhat chaotic status of generic objects vis-à-vis split generic objects has led to an erroneous claim by Jacobs (1999) that the externalization of an internal category has a generic object. What is actually proved by op. cit in Lemma 7.3.2 is that the externalization of an internal category has a split generic object, but this is later claimed (erroneously) to give rise to a generic object in the proof of Corollary 9.5.6. Thus, the claimed result of Corollary 9.5.6, that a fibration is small (equivalent to the externalization of an internal category) if and only if it is globally small (has a generic object) and locally small, is mistaken. To give a correct definition in the terminology of op. cit, one would define globally small categories to assume a weak generic object, as we have done in Definition 24.

3.2 Consequences for tripos theory

Jacobs (1999) sketches in Example 5.3.4 the standard construction of a tripos from a partial combinatory algebra, referring to Hyland et al. (1980) for several parts of the construction (including the generic object); the standard definition of a tripos involves a weak generic object only (Hyland et al. 1980; Pitts 1981; Pitts 2002), a discrepancy that has already been noted by Birkedal (2000), p. 110.

This difference is quite destructive, as the weak generic object of a realizability tripos will not generally be generic, as pointed out by Streicher (2017, Theorem 4.6. Thus, we conclude that definition of tripos proposed by Jacobs (1999) rules out the main examples of naturally occurring triposes.

Remark 54. A final subtlety: over the category of assemblies, the fibration of regular subobjects does indeed have a strong generic object, but this is not part of the structure of the tripos.

3.3 Consequences for polymorphism

The reception in the community studying polymorphism has been to either avoid or tacitly correct the definition of generic object. For instance, Hermida (1993) speaks of weak generic objects and strong generic objects and gives the correct definition of $\lambda{\to},\lambda2,\lambda\omega$ fibration in terms of weak generic objects. On the other hand Birkedal et al. (2005), Johann and Sojakova (2017), Sojakova and Johann (2018), Ghani et al. (2019) deal mainly with the split generic objects, and thus do not seem to run into problems. It can be seen, however, that the examples of (split) $\lambda\Diamond$ -fibrations in the cited works are not in fact (split) $\boldsymbol\lambda\boldsymbol\Diamond$ -fibrations in the sense of Jacobs (1999), because they do not have generic objects. Of course, the problem lies with the definitions rather than the examples.

3.4 Consequences for type theory and algebraic set theory

The idea of a universe in a category has been abstracted from Grothendieck’s universes (Artin et al. 1972) by way of the contributions of a number of authors including Bénabou (1973), Martin-Löf (1975), Street (1980), Joyal and Moerdijk (1995), Hofmann and Streicher (1997), Streicher (2005). In fibered categorical language, a universe usually is a full subfibration that has a weak generic object – potentially equipped with additional structure.

In certain cases, the weak generic object of a universe is also a generic object that is nonetheless not strong; one example is Voevodsky’s construction of a universe of well-ordered simplicial sets in the context of the simplicial model of homotopy type theory, reported by Kapulkin and Lumsdaine (2021): it is strong generic for the fibered category of well-ordered families of simplicial sets and order-preserving morphisms, but only generic when considering morphisms that need not preserve the well-orderings. On the other hand, universes of propositions, such as the subobject classifier of a topos or the regular subobject classifier of a quasitopos, are the main source of strong generic objects in nature.

The theory of universes as applied to type theory on the one hand and algebraic set theory on the other hand motivates two additional variants of generic object:

1. (1) In applications to type theory, it has been increasingly important for universes to have a weak generic object T that satisfies an additional realignment property relative to a class of monomorphisms $\mathcal{M}$ ; in particular, given a span of cartesian maps $U\leftarrowtail X \to T$ where $p({U\leftarrowtail X})\in\mathcal{M}$ , we need an extension $U\to T$ factoring $X\to T$ through $U\rightarrowtail X$ . This realignment property has proved essential for the semantics of univalent universes in homotopy type theory (Gratzer et al. 2022; Kapulkin and Lumsdaine 2021; Shulman 2015, 2019) as well as Sterling’s synthetic Tait computability (Sterling 2021), an abstraction of Artin gluing and logical relations. In Section 4.3, we will discuss the generalization of the realignment property to an arbitrary fibered category as the acyclic generic object, which lies strictly between weak generic and generic objects.

2. (2) In algebraic set theory (Joyal and Moerdijk 1995), universes are considered that enjoy a form of generic object that is even weaker than weak generic object. For each $E\in{\mathscr{E}}$ one only “locally” has a morphism into T; the “very weak” generic objects of algebraic set theory seem to relate to weak generic objects in the same way that weak completeness relates to strong completeness in the context of stack completions (Hyland 1988; Hyland et al. 1990), with important applications to the theory of polymorphism. As these very weak generic objects seem to play a fundamental role, we discuss them in more detail in Section 4.2 as part of our proposal for a new alignment of terminology.

4 A Proposal for a New Alignment of Terminology

Based on the data and experience of the applications of fibered categories in the theory of triposes, polymorphism, and universes in type theory and algebraic set theory, we may now proceed with some confidence to propose a new alignment of terminology for generic objects that better reflects fibered categorical practice. In this section, we distinguish our proposed usage from that of other authors by underlining.

We will define several notions of generic object in conceptual order rather than in order of strength; in Table 1, we summarize our terminology and compare it to several representatives from the literature. In Figure 1, we compare the strength of the different kinds of generic object.

Figure 1. An analysis of the comparability of different notions of generic object, where the rightward direction represents (strictly) decreasing strength.

4.1 Generic objects: Ordinary, skeletal, and gaunt

Let be a fibered category. Our most basic definition below corresponds to the weak generic objects of Jacobs (1999).

Definition 55. A generic object for is defined to be an object $T\in{\mathscr{E}}$ such that for any $X\in {\mathscr{E}}$ there exists a cartesian morphism ${X}\longrightarrow{T}$ .

Definition 56. A generic object $T\in{\mathscr{E}}$ is called skeletal when for any $X\in{\mathscr{E}}$ , there exists a unique ${pX}\longrightarrow{pT}$ such that there exists a cartesian map ${X}\longrightarrow{T}$ lying over ${pX}\longrightarrow{pT}$ .

Definition 57. A generic object $T\in{\mathscr{E}}$ is called gaunt when for any $X\in{\mathscr{E}}$ , any two cartesian morphisms ${X}\longrightarrow{T}$ are equal.

Comment 58. Our skeletal and gaunt generic objects are the same as Jacobs’ generic objects and strong generic objects, respectively. Our terminology is inspired by a comparison between the properties of an internal category $\mathbb{C}$ and its externalization: in particular, the generic object over $\mathbb{C}_0$ is skeletal when $\mathbb{C}$ is a skeletal category and it is gaunt when $\mathbb{C}$ is a gaunt category. Unfortunately, Phoa (1992) has used the word “skeletal” to describe what we call gaunt generic objects; but this usage accords with op. cit.’s unconventional definition of a skeletal category: usually a skeletal category is one in which any two isomorphic objects are equal, but Phoa defines it to be one in which the only isomorphisms are identity maps. Thus, Phoa’s skeletal categories would ordinarily be referred to as gaunt categories.

To illustrate the comparison between (skeletal, gaunt) categories and (skeletal, gaunt) generic objects, respectively, we recall Lemma 42, which is restated in the new terminology as follows:

Corollary 59. Let $\mathbb{C}$ be a small category; then $\mathbb{C}$ is (respectively skeletal, gaunt) if and only if the generic object $T=\{{C}\}_{C\in\mathbb{C}_0}$ for ${\textbf{Fam}}{\mathbb{C}}$ is (respectively skeletal, gaunt).

4.2 Weak generic objects and stack completions

In this section, we are concerned with stacks – a 2-dimensional variation on the concept of a sheaf.

Definition 60. Suppose that a pretopos ${\mathscr{B}}$ is equipped with the structure of a site. Then a fibration is a stack when for any object $X\in {\mathscr{B}}$ and covering sieve $S\subseteq {\mathscr{B}}\downarrow X$ , the canonical restriction functor ${{\mathscr{E}}_X}\longrightarrow{\hom_{\textbf{Fib}_{{\mathscr{B}}}}({S,{\mathscr{E}}})}$ is an equivalence.⁴

Our examples will mainly concern stacks on a pretopos ${\mathscr{B}}$ equipped with its regular topology.

Definition 61 (Frey 2013, Definition 2.3.5) A cartesian morphism ${X}\longrightarrow{Y}$ in a fibered category is called cover-cartesian when is a regular epimorphism.

Definition 62. A weak generic object for is defined to be an object $T\in{\mathscr{E}}$ such that for all $X\in{\mathscr{E}}$ there exists a span of cartesian maps $X\leftarrow\tilde{X}\to T$ where ${\tilde{X}}\longrightarrow{X}$ is cover-cartesian.

Comment 63. Our definition and terminology agrees with that of Streicher (2005, (5.2)) and Battenfeld (2008, Definition 6.3.7), differing only in that both of the cited works specialize the definition for Bénabou-definable full subfibrations of the fundamental fibration of a topos, i.e. full subfibrations that are stacks. Our definition is also identical to the representability axiom (S2) for classes of small maps in algebraic set theory (Joyal and Moerdijk 1995, Definition 1.1).

Remark 64. The notion of weak generic object defined above should be thought of as an internal version of the property of being a generic object – internal to a fibration that is a stack for the regular topology. Indeed, our explicit definition ought to be the translation of ordinary genericity through a generalization of Shulman’s stack semantics (Shulman 2010) that is stated for stacks other than the fundamental fibration . The same (informal) translation is used by Hyland et al. (1990) to correctly define weak equivalences and weak completeness for categories fibered over a regular category.

Weak generic objects in the sense of Definition 62 arise very naturally.

Example 65. Let $\pi:{E}\longrightarrow{U}$ be a morphism in a topos ${\mathscr{B}}$ ; then the class of maps arising as pullbacks of $\pi:{E}\longrightarrow{U}$ determines a full subfibration $[{\pi}]\subseteq\textbf{P}_{{\mathscr{B}}}$ of the fundamental fibration

for which $\pi:{E}\longrightarrow{U}$ is a generic object. The stack completion of $[{\pi}]$ is a weakly (but not necessarily strongly) equivalent full subfibration $\{{\pi}\}\subseteq \textbf{P}_{{\mathscr{B}}}$ , and it can be computed like so: an object of $\{{\pi}\}_{I}$ is a morphism ${X}\longrightarrow{I}$ such that there exists a regular epimorphism

such that the pullback ${X\times_{I}\tilde{I}}\longrightarrow{\tilde{I}}$ lies in $[{\pi}]_{\tilde{I}}$ . In other words, we have the pullback squares in the following configuration:

Unless $[{\pi}]$ was already a stack, it is not necessarily the case that ${E}\longrightarrow{U}$ is a generic object for the stack completion $\{{\pi}\}$ . But Streicher (2005) points out that ${E}\longrightarrow{U}$ is nevertheless a weak generic object for $\{{\pi}\}$ , essentially by definition.

Scenarios of the form described in Example 65 are easy to come by; a canonical example is furnished by the modest objects of a realizability topos as described by Hyland et al. (1990), with critical implications for the denotational semantics of polymorphism.

Example 66 (Hyland et al. 1990). Let $\textbf{Eff}$ be the effective topos (Hyland 1982), and let $\mathsf{N}$ be its object of realizers, i.e. the partitioned assembly given by $\mathbb{N}$ such that $n\Vdash m \in \mathsf{N} \Leftrightarrow m = n$ . Write $\mathsf{P}\subseteq \Omega^{\mathsf{N}\times\mathsf{N}}$ for the the object of $\lnot\lnot$ -closed partial equivalence relations on $\mathsf{N}$ and $\mathsf{P}'\in \textbf{Eff}\downarrow \mathsf{P}$ for the generic $\lnot\lnot$ -closed subquotient of $\mathsf{N}$ ; internally, this is the subquotient $R:\mathsf{P}\vdash \{{x:\mathsf{N}}{x\mathrel{R}x}\}/R$ .

The family $\pi:{\mathsf{P}'}\longrightarrow{\mathsf{P}}$ then induces a full subfibration $[{\pi}]\subseteq\textbf{P}_{\textbf{Eff}}$ spanned by morphisms that arise by pullback from $\pi$ ; an element $[{\pi}]_I$ is an object at stage I that is the subquotient of $\mathsf{N}$ by some partial equivalence defined at stage I. The fibration is small with generic object $\pi$ , but it is not complete. Although for every $\textbf{Eff}$ -indexed diagram ${\mathbb{C}}\longrightarrow{[{\pi}]}$ there “exists” in the internal sense a limit, we cannot globally choose this limit. This situation is referred to by Hyland et al. (1990) as weak completeness as opposed to strong completeness.

In contrast, we may consider the stack completion $\{{\pi}\}$ of $[{\pi}]$ . An element of $\{{\pi}\}_I$ is given by an object E at stage I such that there “exists” (in the internal sense) a partial equivalence relation that it is the quotient of – externally, this means that there is a regular epimorphism ${\tilde{I}}\longrightarrow{I}$ such that $\tilde{I}^*E$ is the subquotient of $\mathsf{N}$ by some partial equivalence relation defined at stage $\tilde{I}$ . The stack $\{{\pi}\}$ is weakly but not strongly equivalent to $[{\pi}]$ ; on the other hand, $\{{\pi}\}$ is complete in the strong sense. Finally, we observe that $\pi:{\mathsf{P}'}\longrightarrow{\mathsf{P}}$ is a weak generic object for the stack completion $\{{\pi}\}$ .

If we pull back $[{\pi}]$ to along the inclusion $i:{\textbf{Asm}}\hookrightarrow{\textbf{Eff}}$ of assemblies/ $\lnot\lnot$ -separated objects in $\textbf{Eff}$ , then we have a complete fibered category $i^*[{\pi}]$ over $\textbf{Asm}$ which turns out to be (strongly) equivalent to the familiar fibration of uniform families of PERs over assemblies. In fact, $i^*[{\pi}]$ is strongly equivalent to $i^*\{{\pi}\}$ – in other words, over assemblies there is no difference between an object that is locally isomorphic to a subquotient of $\mathsf{N}$ and an actual subquotient of $\mathsf{N}$ .

There is another way to think of the situation described at the end of Example 66, using the observations of Streicher (2005) on the relationship between Bénabou’s notion of definable class and stackhood: the class of families of subquotients of $\mathsf{N}$ is not definable in $\textbf{Eff}$ , but it is definable in $\textbf{Asm}$ .

4.3 A new class: acyclic generic objects

Inspired by the crucial realignment property of type theoretic universes (Gratzer et al. 2022) that was discussed in Section 3.4(1), we define a new kind of generic object for an arbitrary fibration that restricts in the case of a full subfibration to a universe satisfying realignment. We refer to Gratzer et al. (2022) for an explanation of the applications of realignment. In this section, let be a fibration and let $\mathcal{M}$ be a class of monomorphisms in ${\mathscr{B}}$ .

Definition 67. A generic object T for

is called $\mathcal{M}$ -acyclic when for any span of cartesian maps in ${\mathscr{E}}$ as depicted below in which

lies in $\mathcal{M}$ ,

there exists a cartesian map ${X}\longrightarrow{T}$ making the following diagram commute in ${\mathscr{E}}$ :

Convention 68. When $\mathcal{M}$ is understood to be the class of all monomorphisms in ${\mathscr{B}}$ , we will simply speak of acyclic generic objects.

All of the examples of acyclic generic objects that we are aware of so far have arisen in the context of the full subfibration spanned by a universe in the sense of Streicher (2005), where acyclicity reduces to the realignment property studied in detail by Gratzer et al. (2022).

Remark 69. It is reasonable to ask whether there is a “weak” version of acyclicity that pertains to stack completions in the same way that weak generic objects relate to generic objects, e.g. by asking for a cover-cartesian morphism and an extension of $U\times_X\tilde{X}\to{U}\to T$ along ${U\times_X \tilde{X}}\longrightarrow{\tilde{X}}$ . It remains somewhat unclear to this author whether this notion is useful, so we do not include it in our proposal.

Comment 70. In the context of universes, the realignment or acyclicity condition has been referred to as “Axiom (2’)” by Shulman (2015), as “strictification” by Orton and Pitts (2016), as “stratification” by Stenzel (2019), as “alignment” by Awodey (2021), and as “strict gluing” by Sterling and Angiuli (2021). See also Riehl (2022) for further discussion.

Origins of the terminology The origin of the term “acyclicity” is explained by Shulman (2019) and Riehl (2022) in essentially the following way. Let ${\mathscr{E}}\subseteq\textbf{P}_{{\mathscr{B}}}$ be a full subfibration equipped with a generic object T; we will write $\textbf{Core}({{\mathscr{E}}})$ for the groupoid core of ${\mathscr{E}}$ , and for any $I\in{\mathscr{B}}$ we will write

for the discrete fibration whose fiber at $J\in {\mathscr{B}}$ is the set of morphisms ${J}\longrightarrow{I}$ . Then, we have a canonical morphism of fibered categories ${\textbf{y}_{{\mathscr{B}}}{pT}}\longrightarrow{\textbf{Core}({{\mathscr{E}}})}$ corresponding under the fibered Yoneda lemma (Streicher 2021, Section 3) to T itself. Realignment for ${\mathscr{E}}$ is then the property that ${\textbf{y}_{{\mathscr{B}}}{pT}}\longrightarrow{\textbf{Core}({{\mathscr{E}}})}$ has the following (2-categorical) extension property with respect to any monomorphism

, in which we write

for the morphism that we identify with $X\in {\mathscr{E}}$ under the fibered Yoneda lemma:

More formally, for any square as above commuting up to an isomorphism $\phi :\lfloor{B}\rfloor\circ \textbf{y}_{{\mathscr{B}}}{m} \cong \lfloor{T}\rfloor\circ \textbf{y}_{{\mathscr{B}}}{\alpha}$ , the extension property states that there exists a (not necessarily unique) morphism $\beta:{I}\longrightarrow{pT}$ and isomorphisms $\phi_0 : \textbf{y}_{{\mathscr{B}}}{\beta}\circ\textbf{y}_{{\mathscr{B}}{m}} \cong \textbf{y}_{{\mathscr{B}}}{\alpha}$ and $\phi_1 : \lfloor{T}\rfloor\circ\textbf{y}_{{\mathscr{B}}}{\beta}\cong \lfloor{B}\rfloor$ such that $\phi$ factors as the pasting of $\phi_0$ and $\phi_1$ . Moreover, as the boundary of $\phi_0$ is discrete, it must be an identity and thus $\beta:{I}\longrightarrow{pT}$ extends $\alpha:{J}\longrightarrow{pT}$ along in the (strict) 1-categorical sense. Under the fibered Yoneda lemma, the isomorphism $\phi : \lfloor{B}\rfloor\circ \textbf{y}_{{\mathscr{B}}}{m}\cong \lfloor{T}\rfloor\circ \textbf{y}_{{\mathscr{B}}}{\alpha}$ corresponds to an isomorphism and the isomorphism $\phi_1 :\lfloor{T}\rfloor\circ \textbf{y}_{{\mathscr{B}}}{\beta}\cong\lfloor{B}\rfloor$ corresponds to an isomorphism that extends along .

In a model categorical setting where $\mathcal{M}$ is understood to be the class of cofibrations, the extension property above expresses that ${\textbf{y}_{{\mathscr{B}}}{pT}}\longrightarrow{\textbf{Core}({{\mathscr{E}}})}$ is an acyclic fibration, whence the terminology.

4.3.1 Incomparability of acyclic and skeletal generic objects

It is not the case that a skeletal generic object need be acyclic. We may consider the following counterexample, which was kindly suggested by one of the anonymous referees of this paper; in what follows, assume that ${\mathscr{B}}$ is a category with finite limits and that G is a group object in ${\mathscr{B}}$ . As in Example 33, we may regard G as an internal groupoid $\textbf{B}{G}$ in ${\mathscr{B}}$ with a single object $({\textbf{B}{G}})_0 =1_{{\mathscr{B}}}$ , such that the hom object $({\textbf{B}{G}})_1$ is exactly G. The externalization $[{\textbf{B}{G}}]$ can be seen to have the same objects as ${\mathscr{B}}$ ; a morphism ${I}\longrightarrow{J}$ in $[{\textbf{B}{G}}]$ is given by a pair of a morphism $f:{I}\longrightarrow{J}$ together with a generalized element $u:{I}\longrightarrow{G}$ . As in any fibered groupoid, every morphism of $[{\textbf{B}{G}}]$ is cartesian. Observe that the object $T = 1_{{\mathscr{B}}}$ is a skeletal generic object in $[{\textbf{B}{G}}]$ ; below, we show that T need not be acyclic.

Lemma 71. The skeletal generic object $T\in [{\textbf{B}{G}}]$ is acyclic if and only if $G\in{\mathscr{B}}$ has the right lifting property with respect to any element of $\mathcal{M}$ .

Proof. Suppose that T is an acyclic generic object, and fix a monomorphism

together with a generalized element $g:{J}\longrightarrow{G}$ in ${\mathscr{B}}$ . We may exhibit a span of cartesian maps in $[{\textbf{B}{G}}]$ as follows, which has a lift by acyclicity:

Above we have exactly a morphism $\hat{g}:{I}\longrightarrow{G}$ extending $g:{J}\longrightarrow{G}$ along . The other direction is analogous.

It is clear that an acyclic generic object need not be skeletal; the above discussion confirms that acyclic and skeletal generic objects are in fact incomparable.

4.4 Splittings and generic objects

We have shown in Section 2.5 that the correct generalization to non-split fibrations of a split generic object in the sense of Jacobs (1999) is what we have proposed to call a generic object, i.e. the weak generic object of op. cit. Thus we conclude that the correct relationship can be established between split $\blacksquare$ -fibrations and $\blacksquare$ -fibrations when re-expressed using our definitions, where $\blacksquare$ ranges over the different kinds of fibered structures (e.g. $\lambda2$ -fibration, polymorphic fibration, etc.). For example, the following definition expresses the correct relationship between $\lambda2$ -fibrations and split $\lambda2$ -fibrations:

Definition 72. A $\lambda2$ -fibration is a fibration with a generic object T, fibered finite products, and simple pT-products and coproducts. A $\lambda2$ -fibration will be called split if all its structure is split.

4.5 In univalent mathematics

The theory of fibered (1-)categories carries over mutatis mutandis to the univalent foundations of mathematics, as shown by Ahrens and Lumsdaine (2019). The pertinent notions of generic object are, however, a bit different in a univalent setting. In particular, gaunt generic objects play a more fundamental role in univalent mathematics than in non-univalent mathematics, because the uniqueness of the classifying squares becomes a statement of contractibility rather than strict uniqueness. In non-univalent mathematics, uncontrived instances of gaunt generic objects tend to follow the pattern of subobject classifiers in representing a fibered poset; in univalent mathematics, we also have object classifiers (univalent universes) which are gaunt generic objects for groupoid cores of the full subfibrations they induce.

Just as in non-univalent mathematics, skeletal generic objects are not expected to play a significant structural role although they may appear when considering the deloopings of groups, as in our 1-categorical examples. The most interesting case is that of acyclic generic objects: the acyclicity property is the correct way to present in non-univalent mathematics a generic object that is gaunt in the homotopical sense, as Shulman has recently argued (Shulman 2022). Thus, in a homotopical/univalent setting, one expects to work directly with gaunt generic objects rather than acyclic ones.

5. Concluding Remarks

For a number of years, the disorder in the variants of generic object has led to a proliferation of subtle differences in terminology between different papers applying fibered categories to categorical logic, type theory, and the denotational semantics of polymorphic types. Based on the kinds of generic object that occur most naturally or have the most utility, we have proposed a unified terminological scheme for generic objects that we believe will meet the needs of scientists working in these areas.