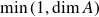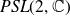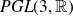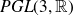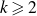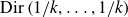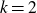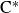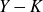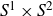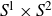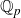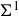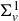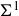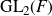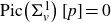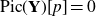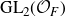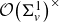Research Article
Projection theorems for linear-fractional families of projections
- Part of:
-
- Published online by Cambridge University Press:
- 08 August 2023, pp. 625-647
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dirichlet law for factorisation of integers, polynomials and permutations
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2023, pp. 649-676
-
- Article
- Export citation
Motivic zeta functions of hyperplane arrangements
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2023, pp. 187-215
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random amenable C*-algebras
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2023, pp. 345-366
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 175 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 October 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Null-homotopic knots have Property R
-
- Published online by Cambridge University Press:
- 20 February 2023, pp. 217-223
-
- Article
- Export citation
Relatively hyperbolic groups with strongly shortcut parabolics are strongly shortcut
- Part of:
-
- Published online by Cambridge University Press:
- 17 April 2023, pp. 367-380
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 175 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 October 2023, pp. b1-b5
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 175 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 June 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Equations of mirrors to log Calabi–Yau pairs via the heart of canonical wall structures
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2023, pp. 381-421
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Picard group of vertex affinoids in the first Drinfeld covering
- Part of:
-
- Published online by Cambridge University Press:
- 13 April 2023, pp. 423-432
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 175 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 June 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
On the integral Hodge conjecture for varieties with trivial Chow group
-
- Published online by Cambridge University Press:
- 17 May 2023, pp. 433-443
-
- Article
- Export citation
Necessary condition for the L2 boundedness of the Riesz transform on Heisenberg groups
- Part of:
-
- Published online by Cambridge University Press:
- 23 May 2023, pp. 445-458
-
- Article
- Export citation
A characterisation of atomicity
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2023, pp. 459-465
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 175 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 August 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
PSP volume 175 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 August 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation