Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2025-01-05T00:44:09.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirichlet law for factorisation of integers, polynomials and permutations

Part of: Finite fields and commutative rings (number-theoretic aspects) Multiplicative number theory Combinatorics Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  06 September 2023

SUN–KAI LEUNG
SUN–KAI LEUNG*
Affiliation:
Département de Mathématiques et de Statistique, Université de Montréal, CP 6128 succ. Centre-Ville, Montréal, QC H3C 3J7, Canada. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $k \geqslant 2$ be an integer. We prove that factorisation of integers into k parts follows the Dirichlet distribution 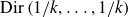$\mathrm{Dir}\left({1}/{k},\ldots,{1}/{k}\right)$ by multidimensional contour integration, thereby generalising the Deshouillers–Dress–Tenenbaum (DDT) arcsine law on divisors where 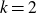$k=2$. The same holds for factorisation of polynomials or permutations. Dirichlet distribution with arbitrary parameters can be modelled similarly.

MSC classification

Primary: 11M32: Multiple Dirichlet series and zeta functions and multizeta values 11N37: Asymptotic results on arithmetic functions 11N60: Distribution functions associated with additive and positive multiplicative functions
Secondary: 05A05: Permutations, words, matrices 05A16: Asymptotic enumeration 11T06: Polynomials
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 175 , Issue 3 , November 2023 , pp. 649 - 676
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bareikis, G. and Mac̆iulis, A.. Cesàro means related to the square of the divisor function. Acta Arith. 156(1) (2012), 83–99.CrossRefGoogle Scholar
Bareikis, G. and Mac̆iulis, A.. Modeling the beta distribution using multiplicative functions. Lith. Math. J. 57(2) (2017), 171–182.CrossRefGoogle Scholar
Bareikis, G. and Mac̆iulis, A.. Bivariate beta distribution and multiplicative functions. Eur. J. Math. 7(4) (2021), 1668–1688.CrossRefGoogle Scholar
de la Bretèche, R. and Tenenbaum, G.. Sur les processus arithmétiques liés aux diviseurs. Adv. in Appl. Probab. 48(A) (2016), 63–76.CrossRefGoogle Scholar
Deshouillers, J.-M. Dress, F. and Tenenbaum, G.. Lois de répartition des diviseurs. I. Acta Arith. 34(4) (1979), 273–285.CrossRefGoogle Scholar
Daoud, M. S. Hidri, A. and Naimi, M.. The distribution law of divisors on a sequence of integers. Lith. Math. J. 55(4) (2015), 474–488.CrossRefGoogle Scholar
Elboim, D. and Gorodetsky, O.. Multiplicative arithmetic functions and the generalised Ewens measure. ArXiv: 1909.00601 (2022).Google Scholar
Feng, B. and Cui, Z.. DDT theorem over square-free numbers in short interval. Front. Math. China 12(2) (2017), 367–375.CrossRefGoogle Scholar
Granville, A.. The anatomy of integers and permutations. preprint (2008), available at: https://dms.umontreal.ca/andrew/PDF/Anatomy.pdf.Google Scholar
Granville, A. and Granville, J.. Prime suspects. The anatomy of integers and permutations, illustrated by Robert J. Lewis (Princeton University Press, Princeton, NJ, 2019).Google Scholar
Granville, A. and Koukoulopoulos, D.. Beyond the LSD method for the partial sums of multiplicative functions. Ramanujan J. 49(2) (2019), 287–319.CrossRefGoogle ScholarPubMed
Hall, R. R.. Sets of multiples. Cambridge Tracts in Math. 118 (Cambridge University Press, Cambridge, 1996).CrossRefGoogle Scholar
Koukoulopoulos, D.. Localised factorisations of integers. Proc. Lond. Math. Soc. (3) 101(2) (2010), 392–426.CrossRefGoogle Scholar
Koukoulopoulos, D.. The distribution of prime numbers. Grad. Stud. Math. 203 (Amer. Math. Soc., 2019).CrossRefGoogle Scholar
Montgomery, H. L. Vaughan, R. C.. Multiplicative number theory. I. Classical theory. Cambridge Stud. Adv. Math. 97 (Cambridge University Press, Cambridge, 2007).CrossRefGoogle Scholar
Nyandwi, S. and Smati, A.. Smati. Distribution laws of pairs of divisors. Integers 13 (2013), paper no. A13, 13.Google Scholar
Nyandwi, S. and Smati, A.. Distribution laws of smooth divisors. ArXiv: 1806.05955 (2018).Google Scholar
Rosen, M.. Number theory in function fields. Grad. Texts in Math. 210 (Springer-Verlag, New York, 2002).CrossRefGoogle Scholar
Stanley, R. P.. Enumerative combinatorics. Vol. 2. Cambridge Stud. Adv. Math. 62 (Cambridge University Press, Cambridge, 1999). With a foreword by Gian–Carlo Rota and appendix 1 by Sergey Fomin.Google Scholar
Tenenbaum, G.. Introduction to analytic and probabilistic number theory, third ed. Grad. Stud. Math. 163 (Amer. Math. Soc., Providence, RI, 2015). Translated from the 2008 French edition by Patrick D. F. Ion.CrossRefGoogle Scholar
Titchmarsh, E. C.. The theory of the Riemann zeta-function, second ed. Grad. Stud. Math. 163 (The Clarendon Press, Oxford University Press, New York, 1986). Edited and with a preface by D. R. Heath–Brown.Google Scholar
Tóth, L.. Multiplicative arithmetic functions of several variables: a survey. Mathematics without boundaries (Springer, New York, 2014), pp. 483–514.CrossRefGoogle Scholar