Research Article
Series identities and reducibility of Kampé de Fériet functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 435-440
-
- Article
- Export citation
Some conditions ensuring the vanishing of harmonic differential forms with applications to harmonic maps and Yang-Mills theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 441-452
-
- Article
- Export citation
On the Dixmier property of simple C*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 75-78
-
- Article
- Export citation
Asymptotic estimates of the eigenvalues of certain positive Fredholm operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 267-284
-
- Article
- Export citation
A boundary estimate for harmonic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-90
-
- Article
- Export citation
Approximating maps and exact C*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-289
-
- Article
- Export citation
On the converse of absolute Abel summability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-456
-
- Article
- Export citation
A theorem about countable decomposability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 457-458
-
- Article
- Export citation
The volume of certain convex sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-97
-
- Article
- Export citation
Norm preserving interpolation sets for polydisc algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-303
-
- Article
- Export citation
Tori in the diffeomorphism groups of simply-connected 4-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 305-314
-
- Article
- Export citation
Locally symmetric homology spheres and an application of Matsushima's formula
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 459-466
-
- Article
- Export citation
Linear invariants of Riemannian almost product manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-106
-
- Article
- Export citation
Imbedding four-manifolds and slicing links
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-110
-
- Article
- Export citation
Random uniform triangles and the alignment problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-322
-
- Article
- Export citation
Totally knotted knots are prime
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 467-472
-
- Article
- Export citation
Multipole expansions for two superposed fluids, each of finite depth
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 323-329
-
- Article
- Export citation
Langer's method for a second order linear ordinary differential equation with a double pole
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-118
-
- Article
- Export citation
More 3-manifolds with multiple knot-surgery and branched-cover descriptions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 473-475
-
- Article
- Export citation
The Variational Principle and natural transformations II. Time dependent theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-341
-
- Article
- Export citation

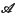 is said to satisfy the Dixmier property if for each element
is said to satisfy the Dixmier property if for each element 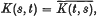 , for – 1 ≤
, for – 1 ≤ 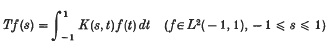
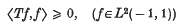
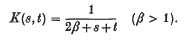
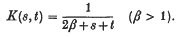
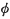 ε
ε 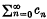 is said to be summable
is said to be summable 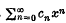 converges to φ(
converges to φ(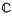
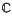 ;
;