Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-11T07:33:46.989Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dixmier property of simple C*-algebras

Published online by Cambridge University Press:  24 October 2008

Norbert Riedel
Norbert Riedel
Affiliation:
Technical University of Munich
Get access Rights & Permissions [Opens in a new window]

Extract

A unital C*-algebra 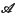is said to satisfy the Dixmier property if for each element x in 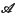the closed convex hull of all elements of the form u*xu, u being a unitary in 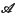, intersects the centre of 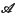((2), 2·7). The von Neumann algebras and also some other classes of C*-algebras are known to satisfy the Dixmier property (cf. (2), (3), (4), (6)). If 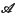is a simple C*-algebra which satisfies the Dixmier property then 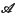has at most one tracial state. In (3) Archbold raised the question whether there exists a unital simple C*-algebra which has at most one tracial state without satisfying the Dixmier property. In the present note we characterize the unital simple C*-algebras with at most one tracial state in terms of a condition which is similar to the Dixmier property, but is in fact formally weaker in the framework of simple C*-algebras. This characterization relies on the method used by Pedersen in (5) in order to show that for a unital simple C*-algebra 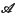which has at most one tracial state and at least one non-trivial projection the linear span of all projections in 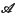is dense in 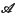As an application we characterize those unital simple C*-algebras with a unique tracial state which satisfy the Dixmier property.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 91 , Issue 1 , January 1982 , pp. 75 - 78
Copyright
Copyright © Cambridge Philosophical Society 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Akeman, C. A., Pedersen, G. K. and Tomiyama, J.Multipliers of C*-algebras. J. Functional Analysis 13 (1973), 277–301.CrossRefGoogle Scholar
(2)Archbold, R. J.An averaging process for C*-algebras related to weighted shifts. Proc. London Math. Soc. 35 (1977), 541–554.CrossRefGoogle Scholar
(3)Archbold, R. J.On the Dixmier property of certain algebras. Math. Proc. Cambridge Phil. Soc. 86 (1979), 251–259.CrossRefGoogle Scholar
(4)Dixmier, J.Lea algèbres d'opérateurg dans l'espace Hilbertien, 2e éd. (Gauthier-Villars Paris, 1969).Google Scholar
(5)Pedersen, G. K.The linear span of projections in simple C*-algebras. J. Operator Theory 4 (1980), 289–296.Google Scholar
(6)Powers, R. T.Simplicity of the C*-algebra associated with the free group on two generators. Duke Math. J. 42 (1975), 151–156.CrossRefGoogle Scholar