Some of Ramanujan's original discoveries about hypergeometric functions and their relation to modular integrals, especially Eisenstein series of negative weight, are still not very well understood. These discoveries take the form of identities that he recorded, without proof, as entries in his notebooks. In the following sections I will introduce some of these entries, discuss their status, give new proofs of several of them and also provide new results of a similar nature.

Let (Gi | i ∈ I) be a family of groups, let F be a free group, and let the free product of F and all the Gi.

Let 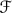denote the set of all finitely generated subgroups H of G which have the property that, for each g ∈ G and each i ∈ I, 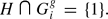By the Kurosh Subgroup Theorem, every element of 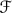is a free group. For each free group H, the reduced rank of H, denoted r(H), is defined as 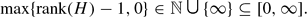To avoid the vacuous case, we make the additional assumption that 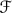contains a non-cyclic group, and we define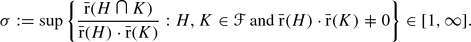We are interested in precise bounds for 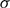. In the special case where I is empty, Hanna Neumann proved that 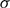∈ [1,2], and conjectured that 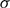= 1; fifty years later, this interval has not been reduced.

With the understanding that ∞/(∞ − 2) is 1, we define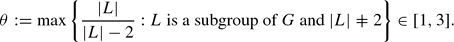

Generalizing Hanna Neumann's theorem we prove that 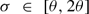, and, moreover, 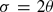whenever G has 2-torsion. Since 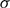is finite, 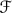is closed under finite intersections. Generalizing Hanna Neumann's conjecture, we conjecture that 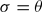whenever G does not have 2-torsion.

The main purpose is to characterise continuous maps that are n-branched coverings in terms of induced maps on the rings of functions. The special properties of Frobenius n-homomorphisms between two function spaces that correspond to n-branched coverings are determined completely. Several equivalent definitions of a Frobenius n-homomorphism are compared and some of their properties are proved. An axiomatic treatment of n-transfers is given in general and properties of n-branched coverings are studied and compared with those of regular coverings.

We study the analogues of the problems of averages and maximal averages over a surface in when the euclidean structure is replaced by that of a vector space over a finite field, and obtain optimal results in a number of model cases.

We construct a pairing on the dual Selmer group over false Tate curve extensions of an elliptic curve with good ordinary reduction at a prime p≥5. This gives a functional equation of the characteristic element which is compatible with the conjectural functional equation of the p-adic L-function. As an application we compute the characteristic elements of those modules – arising naturally in the Iwasawa-theory for elliptic curves over the false Tate curve extension – which have rank 1 over the subgroup of the Galois group fixing the cyclotomic extension of the ground field. We also show that the example of a non-principal reflexive left ideal of the Iwasawa algebra does not rule out the possibility that all torsion Iwasawa-modules are pseudo-isomorphic to the direct sum of quotients of the algebra by principal ideals.

We show that in quasi-logarithmic additive number systems all partition sets have asymptotic density, and we obtain a corresponding monadic second-order limit law for adequate classes of relational structures. Our conditions on the local counting function p(n) of the set of irreducible elements of allow situations which are not covered by the density theorems of Compton [6] and Woods [15]. We also give conditions on p(n) which are sufficient to show the assumptions of Compton's result are satisfied, but which are not necessarily implied by those of Bell and Burris [2], Granovsky and Stark [8] or Stark [14].

We show that the number of distinct non-parallel lines passing through two conjugates of an algebraic number α of degree d ≥ 3 is at most [d2/2]-d+2, its conjugates being in general position if this number is attained. If, for instance, d ≥ 4 is even, then the conjugates of α ∈ of degree d are in general position if and only if α has 2 real conjugates, d-2 complex conjugates, no three distinct conjugates of α lie on a line and any two lines that pass through two distinct conjugates of α are non-parallel, except for d/2-1 lines parallel to the imaginary axis. Our main result asserts that the conjugates of any Salem number are in general position. We also ask two natural questions about conjugates of Pisot numbers which lead to the equation α1+α2=α3+α4 in distinct conjugates of a Pisot number. The Pisot number shows that this equation has such a solution.

We study H*(P), the mod p cohomology of a finite p-group P, viewed as an –module. In particular, we study the conjecture, first considered by Martino and Priddy, that, if e ∈ is a nonzero idempotent, then the Krull dimension of eH*(P) equals the rank of P. We prove this for all p-groups when p is odd, and for many 2–groups.

Suppose that A and A′ are subsets of ℤ/Nℤ. We write A+A′ for the set {a+a′:a ∈ A and a′ ∈ A′} and call it the sumset of A and A′. In this paper we address the following question. Suppose that A1,. . .,Am are subsets of ℤ/Nℤ. Does A1+· · ·+Am contain a long arithmetic progression?

The situation for m=2 is rather different from that for m ≥ 3. In the former case we provide a new proof of a result due to Green. He proved that A1+A2 contains an arithmetic progression of length roughly where α1 and α2 are the respective densities of A1 and A2. In the latter case we improve the existing estimates. For example we show that if A ⊂ ℤ/Nℤ has density then A+A+A contains an arithmetic progression of length Ncα. This compares with the previous best of Ncα2+ϵ.

Two main ingredients have gone into the paper. The first is the observation that one can apply the iterative method to these problems using some machinery of Bourgain. The second is that we can localize a result due to Chang regarding the large spectrum of L2-functions. This localization seems to be of interest in its own right and has already found one application elsewhere.

We show that the 2-category of partial combinatory algebras, as well as various related categories, admit a certain type of lax comma objects. This not only reveals some of the properties of such categories, but it also gives an interpretation of iterated realizability, in the following sense. Let φ: A → B be a morphism of PCAs, giving a comma object A ⋉φB. In the realizability topos RT(B) over B, the object (A, φ) is an internal PCA, so we can construct the realizability topos over (A, φ). This topos is equivalent to the realizability topos over the comma-PCA A ⋉φB. This result is both an analysis and a generalization of a special case studied by Pitts in the context of the effective monad.

Let θ be a Jordan homomorphism from an algebra A into an algebra B. We find various conditions under which the restriction of θ to the commutator ideal of A is the sum of a homomorphism and an antihomomorphism. Algebraic results, obtained in the first part of the paper, are applied to the second part dealing with the case where A and B are C*-algebras.

This paper discusses the Brauer–Manin obstruction on double covers of the projective plane branched along a plane section of a Kummer surface from both the practical and the theoretical points of view. Theoretical highlights include the determination of a complete set of generators for the Brauer group; on the practical side, we give several surfaces with a Brauer–Manin obstruction and verify that the Brauer–Manin obstruction is the only one for a collection of several thousand surfaces of this type.

We establish isomorphisms between certain specializations of BMW algebras and the symmetric squares of Temperley–Lieb algebras. These isomorphisms imply a link-polynomial identity due to W. B. R. Lickorish. As an application, we compute the closed images of the irreducible braid group representations factoring over these specialized BMW algebras.

Mislin and Talelli showed that a torsion-free group in with periodic cohomology after some steps has finite cohomological dimension. In this note we look at similar questions for groups with torsion by considering Bredon cohomology. In particular we show that every elementary amenable group acting freely and properly on some × Sm admits a finite dimensional model for G.

We explore an alternative definition of unit in a monoidal category originally due to Saavedra: a Saavedra unit is a cancellable idempotent (in a 1-categorical sense). This notion is more economical than the usual notion in terms of left-right constraints, and is motivated by higher category theory. To start, we describe the semi-monoidal category of all possible unit structures on a given semi-monoidal category and observe that it is contractible (if non-empty). Then we prove that the two notions of units are equivalent in a strong functorial sense. Next, it is shown that the unit compatibility condition for a (strong) monoidal functor is precisely the condition for the functor to lift to the categories of units, and it is explained how the notion of Saavedra unit naturally leads to the equivalent non-algebraic notion of fair monoidal category, where the contractible multitude of units is considered as a whole instead of choosing one unit. To finish, the lax version of the unit comparison is considered. The paper is self-contained. All arguments are elementary, some of them of a certain beauty.

MacLane cohomology is an algebraic version of the topological Hochschild cohomology. Based on the computation of the third author (see Appendix) we obtain an interpretation of the third Mac Lane cohomology of rings using certain kind of crossed extensions of rings in the quadratic world. Actually we obtain two such interpretations corresponding to the two monoidal structures on the category of square groups.

Any 2-bridge knot in S3 has a bridge sphere from which any other bridge surface can be obtained by stabilization, meridional stabilization, perturbation and proper isotopy.

We show that in a special Moufang set, either the root groups are elementary abelian 2-groups, or the Hua subgroup H (= the Cartan subgroup) acts “irreducibly” on U, i.e. the only non-trivial H-invariant subgroup of a root group normalized by H is the whole root group.

Generalizing the notion of left amenability for so-called F-algebras [12], we study the concept of ϕ-amenability of a Banach algebra A, where ϕ is a homomorphism from A to ℂ. We establish several characterizations of ϕ-amenability as well as some hereditary properties. In addition, some illuminating examples are given.

Infinite presentations are given for all of the higher Torelli groups of once-punctured surfaces. In the case of the classical Torelli group, a finite presentation of the corresponding groupoid is also given, and finite presentations of the classical Torelli groups acting trivially on homology modulo N are derived for all N. Furthermore, the first Johnson homomorphism, which is defined from the classical Torelli group to the third exterior power of the homology of the surface, is shown to lift to an explicit canonical 1-cocycle of the Teichmüller space. The main tool for these results is the known mapping class group invariant ideal cell decomposition of the Teichmüller space.

This new 1-cocycle is mapping class group equivariant, so various contractions of its powers yield various combinatorial (co)cycles of the moduli space of curves, which are also new. Our combinatorial construction can be related to former works of Kawazumi and the first-named author with the consequence that the algebra generated by the cohomology classes represented by the new cocycles is precisely the tautological algebra of the moduli space.

There is finally a discussion of prospects for similarly finding cocycle lifts of the higher Johnson homomorphisms.