Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kuhn, Nicholas J.
2007.
Primitives and central detection numbers in group cohomology.
Advances in Mathematics,
Vol. 216,
Issue. 1,
p.
387.
Himstedt, Frank
and
Symonds, Peter
2009.
Equivariant Hilbert series.
Algebra & Number Theory,
Vol. 3,
Issue. 4,
p.
423.
Kuhn, Nicholas J.
2013.
Nilpotence in group cohomology.
Proceedings of the Edinburgh Mathematical Society,
Vol. 56,
Issue. 1,
p.
151.
Cohen, Frederick R.
Hemmer, David J.
and
Nakano, Daniel K.
2016.
The Lie module and its complexity.
Bulletin of the London Mathematical Society,
Vol. 48,
Issue. 1,
p.
109.


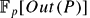 –module. In particular, we study the conjecture, first considered by Martino and Priddy, that, if
–module. In particular, we study the conjecture, first considered by Martino and Priddy, that, if 