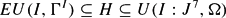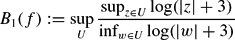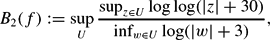Research Article
On decomposition numbers and Alvis–Curtis duality
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 509-520
-
- Article
- Export citation
Deficiency and abelianized deficiency of some virtually free groups
-
- Published online by Cambridge University Press:
- 01 September 2007, pp. 257-264
-
- Article
- Export citation
The automorphism group of an affine quadric
-
- Published online by Cambridge University Press:
- 01 July 2007, pp. 1-8
-
- Article
- Export citation
Polynomial bounds for equivalence of quadratic forms with cube-free determinant
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 521-532
-
- Article
- Export citation
On a parametric family of Thue inequalities over function fields
-
- Published online by Cambridge University Press:
- 01 July 2007, pp. 9-23
-
- Article
- Export citation
Special units and ideal class groups of extensions of imaginary quadratic fields
-
- Published online by Cambridge University Press:
- 01 September 2007, pp. 265-270
-
- Article
- Export citation
The loop problem for monoids and semigroups
-
- Published online by Cambridge University Press:
- 01 September 2007, pp. 271-289
-
- Article
- Export citation
On factorials which are products of factorials
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 533-542
-
- Article
- Export citation
On the actions of a locally compact group on some of its semigroup compactifications
-
- Published online by Cambridge University Press:
- 01 July 2007, pp. 25-39
-
- Article
- Export citation
On motivic principal value integrals
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 543-555
-
- Article
- Export citation
Total curvature, ropelength and crossing number of thick knots†
-
- Published online by Cambridge University Press:
- 01 July 2007, pp. 41-55
-
- Article
- Export citation
Finitary and Artinian-finitary groups
-
- Published online by Cambridge University Press:
- 01 September 2007, pp. 291-305
-
- Article
- Export citation
Geometric collections and Castelnuovo–Mumford regularity
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 557-578
-
- Article
- Export citation
Symmetric pairs and associated commuting varieties
-
- Published online by Cambridge University Press:
- 01 September 2007, pp. 307-321
-
- Article
- Export citation
Reversible maps in the group of quaternionic Möbius transformations
-
- Published online by Cambridge University Press:
- 01 July 2007, pp. 57-69
-
- Article
- Export citation
Explicit Noether–Lefschetz for arbitrary threefolds
-
- Published online by Cambridge University Press:
- 01 September 2007, pp. 323-342
-
- Article
- Export citation
On Manin's conjecture for singular del Pezzo surfaces of degree four, II
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 579-605
-
- Article
- Export citation
Quasiconformal homogeneity of hyperbolic surfaces with fixed-point full automorphisms
-
- Published online by Cambridge University Press:
- 01 July 2007, pp. 71-84
-
- Article
- Export citation
Stable sandwich classification theorem for classical-like groups
-
- Published online by Cambridge University Press:
- 01 November 2007, pp. 607-619
-
- Article
- Export citation
Uniformly bounded components of normality
-
- Published online by Cambridge University Press:
- 01 July 2007, pp. 85-101
-
- Article
- Export citation

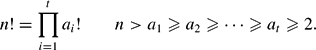
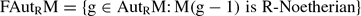
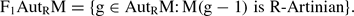
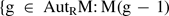 embeds into some finitely generated R-module which does not fit our earlier pattern of generalized finitary groups as described in [
embeds into some finitely generated R-module which does not fit our earlier pattern of generalized finitary groups as described in [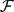 on a smooth projective variety with a geometric collection, two spectral sequences: the first one abuts to
on a smooth projective variety with a geometric collection, two spectral sequences: the first one abuts to 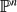 and for a suitable geometric collection of coherent sheaves on
and for a suitable geometric collection of coherent sheaves on 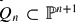 (
(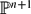 .
.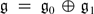 be a
be a 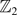 -grading of a simple Lie algebra
-grading of a simple Lie algebra 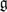 . The commuting variety associated with such a grading is the variety of pairs of commuting elements from
. The commuting variety associated with such a grading is the variety of pairs of commuting elements from 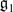 . We study the problem of irreducibility of these varieties. Using invariant-theoretic technique, we present new instances of reducible and irreducible commuting varieties.
. We study the problem of irreducibility of these varieties. Using invariant-theoretic technique, we present new instances of reducible and irreducible commuting varieties. . In fact, if
. In fact, if 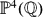 , then the height zeta function
, then the height zeta function 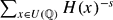 is analytically continued to the half-plane ℜ
is analytically continued to the half-plane ℜ