Research Article
An examination of Whitham's exact averaged variational principle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-344
-
- Article
- Export citation
Bounds for surface solitary waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-358
-
- Article
- Export citation
Classical electrodynamics: the equation of motion
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 359-367
-
- Article
- Export citation
Transient stresses in an elastic half space resulting from the frictionless indentation of a rigid axially symmetric conical die
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-379
-
- Article
- Export citation
Exact analysis of simply supported rhombic plates under uniform pressure
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-388
-
- Article
- Export citation
A note on the percolation probabilities of pairs of closely similar lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 389-392
-
- Article
- Export citation
Corrigendum
On isotropic tensors
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 393
-
- Article
-
- You have access
- Export citation
Front matter
PSP volume 76 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 76 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

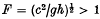 , where
, where