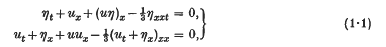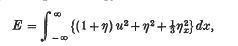Research Article
Spindle-shaped drops in a viscous extensional flow
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 529-536
-
- Article
- Export citation
Convergence of non-homogenous stochastic chains. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-182
-
- Article
- Export citation
Constructing maximal geodesics in strongly causal space-times
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-190
-
- Article
- Export citation
Multi-valued solutions of the wave equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 335-341
-
- Article
- Export citation
The Variational Principle and natural transformations I. Autonomous dynamical systems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 537-560
-
- Article
- Export citation
Proceedings of meetings
Proceedings of the meetings held during the session 1980-1981
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 561-567
-
- Article
- Export citation
Research Article
An acceleration condition for b-incomplete timelike curves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 191-193
-
- Article
- Export citation
Solitary wave solutions for a model of the two-way propagation of water waves in a channel
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 343-360
-
- Article
- Export citation
Front matter
PSP volume 90 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Stability of universal unfoldings: a correction
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-196
-
- Article
- Export citation
The structure of the solution set for the Yang-Mills equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 361-372
-
- Article
- Export citation
Back matter
PSP volume 90 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b14
-
- Article
-
- You have access
- Export citation
Front matter
PSP volume 90 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Invariance relations in thermoelasticity with generalized variables
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-384
-
- Article
- Export citation
Back matter
PSP volume 90 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
PSP volume 90 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 90 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation