The Fibonacci and Lucas polynomials Fn(z) and Ln(z) are denned. These reduce to the familiar Fibonacci and Lucas numbers when z = 1. The polynomials are shown to satisfy a second order linear difference equation. Generating functions are derived, and also various simple identities, and relations with hypergeometric functions, Gegenbauer and Chebyshev polynomials.

In this note we shall study random labelled graphs. Denote by

the set of all graphs with n given labelled vertices and M(n) edges. As usual, we turn (M(n)) into a probability space by giving all graphs the same probability. The question we address ourselves to is the following. Given a graph H and a constant p, 0 < p < 1, for what functions M(n) is it true that the probability PM(n)(H ⊂ G) that a graph G∈ (M(n)) contains H tends to p as n∞→? This question was posed by Erdös and Rényi (3), (4), who also proved several beautiful and surprising theorems. In order to state the main general result of Erdös and Rényi in this direction, and for our use later, we introduce some definitions.

Let 0 < λ1 < λ2 < … be an increasing sequence of positive reals tending to infinity, and let ν1, ν2 be two (finite) signed measures on ℝ+ such that

for all k. It was originally proved by Müntz (12) that, if

then ν1 = ν2, and, conversely, if this condition fails, then there exist distinct ν1 and ν2 satisfying (1).

We denote by ∥…∥ the distance to the nearest integer. Let ε be an arbitrary positive number. Danicic(6) showed that for N > c1(s, ε) and a quadratic form Q(x1, …, xs) there exist integers n1, …, ns with

having

This paper relates the concept of n-connection for graphs to Tutte's theory of n-connection for matroids (12). In particular, we show how Tutte's definition may be modified to give a matroid concept directly generalizing the graph-theoretic notion of n-connection.

In this paper we consider certain questions concerning the differential geometry of generic hypersurfaces in ℝn. Our results prove, for example, that the curve of rib points of a generic surface in ℝ3 has transverse self-intersections.

In (4) Porteous discussed (amongst other things) the generic geometry of curves and surfaces in ℝ3. Subsequently Looijenga ((3) and see also (5)) gave a more precise definition of the term generic and showed that an open dense subset of smooth embeddings of manifolds in Euclidean space were indeed generic.

Let P(x) denote a polynomial with degree n and integer coefficients. By the height h of P we mean the maximum of the absolute values of the coefficients.

Let i: Y ↪ X be an inclusion map of non-singular irreducible algebraic quasi-projective varieties defined over an algebraically closed field. Let E be an algebraic vector bundle over X and H be a sub-bundle of the induced bundle, i*E. If j:F(H) ↪ F(E) is the corresponding inclusion map of (incomplete) flag bundles, then we derive the normal bundle N(F(H), F(E)) in terms of the bundles H and E, the tangent bundles of Y and X as well as the tautological bundles over F(H).

In 1975 A. Baker and J. Coates published a paper bearing the same title (2). Since the introduction to their paper can be used in this paper very appropriately, I shall quote large parts of it here.

Let A be a (commutative, Noetherian) local ring (with identity) and let a1,…, an be a system of parameters (s.o.p.) for A. A (not necessarily finitely generated) A-module M is said to be a big Cohen–Macaulay.A-module with respect to a1,…, an if a1,…, an is an M-sequence, that is if M ‡ = (a1,…, an) M and, for each i = 1,…, n,

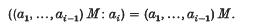
One of the main open problems in commutative algebra at the present time is that of establishing the existence of a big Cohen–Macaulay module with respect to a specified s.o.p. in an arbitrary local ring. The work and writings of Hochster, such as (5), show that, if the existence of such modules could be established, then several conjectures in commutative algebra, some of which are quite long-standing, would be settled. Moreover, Hochster has established the existence of such big Cohen–Macaulay modules whenever the local ring A concerned contains a field as a subring, or has dimension not exceeding 2: see ((5), chapters 4, 5) and (4).

In (10), M. S. Narasimhan and S. Ramanan proved a theorem to the effect that a certain conic bundle associated with a non-singular quadratic complex does not come from a vector bundle ((10), proposition 8·1); a similar topological result was proved in (12). In the course of attempting to extend these results to the singular case, I found that I wanted to use some results on conic bundles which were not readily available in the literature. The object of this note is to give proofs of these results; the work on quadratic complexes is still in progress and the first part will appear shortly (13). A further application will appear in (14).

This paper considers the relationship between the automorphism group of a torsion-free nilpotent group and the automorphism groups of its subgroups and factor groups. If G2 is the derived group of the group G let Aut (G, G2) be the group of automorphisms of G which induce the identity on G/G2, and if B is a subgroup of Aut G let B¯ be the image of B in Aut G/Aut (G, G2). A p–group or torsion-free group G is said to be special if G2 coincides with Z(G), the centre of G, and G/G2 and G2 are both elementary abelian p–groups or free abelian groups.

In a previous paper, M. Georgiacodis and the author proved that there are no non-trivial Moore geometries of diameter greater than 12. Here, it is proved that there are none of diameter greater than 4.

1. The present paper continues the investigation begun in (5). This earlier paper concluded with the description of a pencil P of canonical curves of genus 6 on a del Pezzo quintic surface F, but had first to describe the relevant features of the mapping of prime sections of F on a plane p by cubic curves circumscribing a quadrangle in p. It remains now to consider F and P in their ambient [5] in relation to G, the group, isomorphic to the symmetric group of degree 5, of self-projectivities of F.

Throughout this paper F denotes a (commutative) field. Let XF denote the class of all groups G such that every irreducible FC-module has finite dimension over F. In (1) P. Hall showed that if F is not locally finite and if G is polycyclic, then G∈XF if and only if G is abelian-by-finite. Also in (1), if F is locally finite he proved that every finitely generated nilpotent group is in XF and he conjectured that XF should contain every polycyclic group. This turned out to be very difficult, but a positive solution was eventually found by Roseblade, see (8). Meanwhile Levič in (4) had started a systematic investigation of the classes XF. Although his paper contains a number of errors, obscurities and omissions, it remains an interesting work, and it, or more accurately its recent translation, stimulated this present paper.

Let G be a finite group and let g be the augmentation ideal of the integral group ring G. Following Gruenberg(5) we let (g̱) denote the category whose objects are short exact sequences of zG-modules of the form and in which the morphisms are commutative diagrams

In this paper we describe the projective objects in this category. These are the objects which satisfy the usual categorical definition of projectivity, but they may also be characterized as the short exact sequences

in which P is a projective module.

The purpose of this series of papers is to present a general theory of Banach modules and to give some applications of it. The applications of the theory arise from observations that certain important notions of functional analysis are very closely related to certain Banach algebras and thereby to a module structure. This holds in particular for Banach lattices (which are C(X)-modules), interpolation spaces, tensor products and operator ideals.

The spaces Lp(, φ) for 1 ≤ p ≤ ∞, where φ is a faithful semifinite normal trace on a von Neumann algebra , are defined in (10),(2),(14). The problem of determining the general form of an isometry of one such space into another has been studied in (i), (6), (9), (12), (5). Our main result, Theorem 2, is a characterization of such isometries for 1 ≤ p ≤ ∞, ≠ 2. The method of proof is based on that of (7), where isometries between Lp function spaces are characterized. The main step in the proof is Theorem 1, which gives the conditions under which equality holds in Clarkson's inequality.

The algebraic tensor product A1⊗A2 of two Banach algebras is an algebra in a natural way. There are certain norms α on this tensor product for which the multiplication is continuous so that the completion, A1αA2, is a Banach algebra. The representation theory of such tensor products is the subject of this paper. It will be shown that, under certain simple conditions, the tensor product of two semi-simple Banach algebras is semi-simple although, without these conditions, the result fails.

For a continuous function f(x) on the reals or on the circle T (continuous and 2π periodic) we say that f(x) belongs to the generalized Lipschitz class, denoted by f ∈ Lip* α, if

where and Δhf(x) = f(x + ½h)−f(x−½h). For a convolution approximation process given by

where

we shall investigate equivalence relations between the asymptotic behaviour of (d/dx)rAn(f, x) and f ∈ Lip* α.