No CrossRef data available.
The projective extensions of a finite group
Published online by Cambridge University Press: 24 October 2008
Extract
Let G be a finite group and let g be the augmentation ideal of the integral group ring 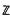 G. Following Gruenberg(5) we let (g̱) denote the category whose objects are short exact sequences of zG-modules of the form
G. Following Gruenberg(5) we let (g̱) denote the category whose objects are short exact sequences of zG-modules of the form 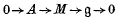 and in which the morphisms are commutative diagrams
and in which the morphisms are commutative diagrams
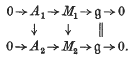
In this paper we describe the projective objects in this category. These are the objects which satisfy the usual categorical definition of projectivity, but they may also be characterized as the short exact sequences

in which P is a projective module.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 2 , September 1981 , pp. 251 - 257
- Copyright
- Copyright © Cambridge Philosophical Society 1981


