We give a quick proof of a result of A. Nagel and E. M. Stein concerning the boundedness of certain generalizations of the Hardy-Littlewood maximal operator.

Let X, X1, X2,… be a sequence of non-degenerate i.i.d. random variables with common distribution function F. For 1 ≤ j ≤ n, let mn(j) be the number of Xi satisfying either |Xi| > |Xj|, 1 ≤ i ≤ n, or |Xi| = |Xj|, 1 ≤ i ≤ j, and let (r)Xn = Xj if mn(j) = r. Thus (r)Xn is the rth largest random variable in absolute value from amongst X1, …, Xn with ties being broken according to the order in which the random variables occur. Set (r)Sn = (r+1)Xn + … + (n)Xn and write Sn for (0)Sn. We will refer to (r)Sn as a trimmed sum.

For stochastic processes which are induced by a signed measure, the Andersen-Jessen theorem asserts almost sure convergence and yields the identification of the limit. This result has been extended to real and vector-valued stochastic processes which are induced by a finitely additive set function or a set function process. In the present paper, we study the structure of such induced stochastic processes in order to locate the Andersen-Jessen theorem and its extensions in the family of convergence theorems for martingales and their generalizations. As an application of these results, we also show that the Andersen-Jessen theorem and its extensions can be deduced from the convergence theorems for conditional expectations and positive supermartingales.

The paper is concerned with properties of the Dirichlet series where {λn} is a strictly increasing unbounded sequence of real numbers with λ1 > 0. One of the main Tauberian results proved is that if a1 ≥ 0, an > 0 for n = 2, 3, …, a(x) ≤ ∞ for all x ≥ 0, An:= a1 + a2 + … + an → ∞, an λn = o((λn+1-λn)An), an λn sn > − H(λn+1 − λn) An and then A new summability method Dλ, a based on the Dirichlet series a(x) is defined and its relationship to the weighted mean method Ma investigated.

1. We use Eα to denote the Euler transformation obtained as the special case of the Hausdorff transformation (H, μn) in which μn = αn (see [5], §§64, 72; in the notation of Hardy's book [1], our Eα is (E, q) with q = (1 − α)/α). Eα is regular if and only if 0 < α < 1, and in this range Eα increases in strength as α decreases since EαEβ = Eαβ. Also, E1 = I, the identity transformation.

Abelian theorems for the H-transform of functions and generalized functions are obtained as the complex variable of the transform approaches zero or infinity in a wedge domain in the right half plane. Quasi-asymptotic behaviour (q.a.b.) of the H-transformable generalized functions is defined. A structure theorem for generalized functions possessing q.a.b. is proved and is applied to obtain the asymptotic behaviour of the H-transform of generalized functions having q.a.b. The theorems are illustrated by examples.

A basic problem of the theory of Markov processes is to find a semigroup S of operators on the bounded Borel measurable functions on ℝd, such that S is given by a transition function, and

for all f belonging to the domain of a given second-order elliptic differential operator D. A process is constructed from the transition function associated with S, and then one hopes to realize the process as one with continuous paths [2].

It has recently been shown [7, 8, 4] that Markov dilations of quantum dynamical semigroups may be constructed by solving corresponding quantum stochastic differential equations. These equations may be interpreted as describing the evolution of a quantum system with a singular coupling to a Boson reservoir, moreover, when solutions are combined with the free evolution of the reservoir, a reversible evolution results which may be interpreted as that of the system plus reservoir. It is the purpose of the present paper to characterize the above stochastic evolutions essentially by a condition of with respect to the free evolution.

The purpose of this article is to derive a set of ‘easily verifiable’ sufficient conditions for the asymptotic stability of the trivial solution of a class of linear neutral integro-delay-differential equations of the form

where ẋ denotes the right derivative, and then generalize the result to a vector system. Asymptotic stability of the trivial solution of the form (1·1) and several of its variants has been considered by many authors (see the discussion at the end). Also, there exists a well developed fundamental theory for neutral delay-differential equations (e.g. existence, uniqueness, continuous dependence etc. of solutions; see for instance the survey article by Akhmerov[1] and the references in it); however there exists no ‘easily verifiable’ sufficient condition for the asymptotic stability of the trivial solution of (1·1). By the term ‘easily verifiable’ we mean a verification which is as easy as in the case of Routh-Hurwitz criterion or the diagonal dominance condition of a matrix. A number of results which are valid for linear autonomous ordinary and delay-differential equations cannot be generalized (or extended) to neutral equations. It has been shown by Gromova and Zverkin [8] that a linear neutral differential equation can have unbounded solutions even though the related characteristic equation has only purely imaginary roots (see also Gromova[7], Datko[3], Snow [16], Brumley [2]); such behaviour is not possible in the case of ordinary or (non-neutral) delay-differential equations. It is known (theorem 6·1 of Henry [10]) that if the characteristic equation associated with a only with negative real parts and if all the roots are uniformly bounded away from the imaginary axis, then asymptotic stability of the trivial solution can be asserted.

A direct and simple approach, utilizing Watson's lemma, is presented for obtaining an approximate solution of a three-part Wiener-Hopf problem associated with the problem of diffraction of a plane wave by a soft strip.

Let D(R) be the Schwartz space of C∞ functions with compact support on R and let H(D) be the space of all C∞ functions defined on R for which every element is the Hilbert transform of an element in D(R), i.e.

where the integral is defined in the Cauchy principal-value sense. Introducing an appropriate topology in H(D), Pandey [3] defined the Hilbert transform Hf of f ∈ (D(R))′ as an element of (H(D))′ by the relation

and then with an appropriate interpretation he proved that

.

In this paper we give an intrinsic description of the space H(D) and its topology, thereby providing a solution to an open problem posed by Pandey ([4], p. 90).

1. Let El (l = 0,1,2, …) be the eigenspaces of the Laplacian on the standard 2-sphere S2. Consider the function r2. 4: El −{0} → R given by

Stanton and Weinstein proved in [1] that r2, 4 was locally maximized by the ‘highest weight’ function . This note is to simplify part of their proof, namely that of the negativity of .

In his monograph [2], Doob presented the theories of quasi-bounded and singular functions associated with the Laplace and heat equations. In particular, on p. 712, he proved in the classical case that a potential is quasi-bounded if and only if its associated measure vanishes on polar sets. However, on p. 714, he proved only weaker results for the thermic case, namely that a potential is quasi-bounded (i) if its associated measure vanishes on semi-polar sets, and (ii) only if its measure vanishes on polar sets. The main purpose of this note is to establish that the exact analogue of the result for the classical case holds for the thermic case. We also use a related theorem on thermal potentials, to prove a second characterization of those which are quasi-bounded, analogous to one due to Arsove and Leutwiler for the classical case. We also give the corresponding characterizations of singular thermal potentials.

Unlike their counterparts for the Laplace's equation, the known results on heat capacity and parabolic measure are rather incomplete. We make a few comments on these two areas.

The aim of this paper is to give some results on the determination of Hamiltonian structure for a set of evolutionary equations, either differential or non-local. There are several reasons why the recognition of Hamiltonian structure is important. Firstly, as in the case of Lagrangian systems, conservation laws are often connected with symmetry groups of the equations. This point is addressed in §4. Secondly, variational principles for steady solutions can often be found by restricting attention to the steady equations. Connected to the second point, methods have been developed by Arnol'd[2] and more recently by Marsden, Weinstein etc. (see, e.g. [24]) to study the nonlinear stability of steady solutions, on lines similar to the proof of nonlinear stability for the solitary-wave solution of the Korteweg–de Vries equation by Benjamin [4] and Bona[9].

There is an extensive literature on Liénard's equation

and numerous criteria for the existence of limit cycles have been developed: see the survey of Staude[7], for example. Broadly speaking, such results are proved in one of two ways: a bounded solution is shown to exist and the Poincaré–Bendixson theorem used, or an ‘a priori’ bound for periodic solutions is obtained and the methods of degree theory utilized.

Much attention has been devoted over the years to the sine-Gordon equation φuv = sin φ (e.g. [2] and references therein). Of fundamental significance is the existence of a countably infinite set of conservation laws, which arises from a corresponding set of symmetries (e.g. [6, 7]).

‘On the global attractivity ina generalized delay-logistic differential equation’

In the proof of Theorem 3·1, the function space and its topology are incorrect, The correct function space and its topology with the related modifications are given below, which will replace the contents of the last line of page 188 and the first eight lines of page 189 of the above article.

Let B denote the real linear space of all continuous functions defined on [0, ∞)topologized by a separating family of seminorms Pn, where

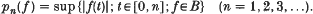
Since p1 ≤ p2 ≤ p3 ≤ …, the sets

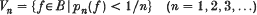
form a convex local base for the topology of B. The topology generated by {Vn} is also compatible with that of the metric d, where

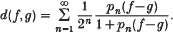
Thus B becomes a metrizable, Hausdorif, locally convex linear topological space. The strong version of the Tychonoff fixed-point theorem of S. A. Morris and E. S. Noussair (Mat. Čs. 25 (1975), 165–172) states ‘If T is a continuous mapping of a convex subset A of a Hausdorff locally convex linear topological space B into a compact subset of A then T has a fixed point’. In the following, the compactness of the image T(A) ⊂ A will follow from an application of the generalized version of Arzela's theorem found in J. R. Munkres (Topology, A first course, Prentice-Hall, 1975, p. 292). Note that the set A is not closed in B but is convex; we will show below that the image set T(A) is contained in A and the members of T(A) are pointwise bounded by (3·16) and pointwise equicontinuous, from which the sequential compactness of T(A) in the topology of compact convergence will follow by the generalized Arzela's theorem; since the real line is metrizable, such a sequential compactness implies sequential compactness in the compact-open topology of T(A); but the set T(A) is itself metrizable by d with a topology compatible with the compact-open topology. Thus the sequential compactness of T(A) in the compact-open topology implies the compactness of the set T(A) in the compact-open topology. Thus it is sufficient to show the pointwise boundedness and equicontinuity of elements of T(A).