Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T11:42:33.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Tauberian and other theorems concerning Dirichlet's series with non-negative coefficients

Published online by Cambridge University Press:  24 October 2008

David Borwein
David Borwein
Affiliation:
Department of Mathematics, University of Western Ontario, London, Ont. N6A 5B7, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper is concerned with properties of the Dirichlet series 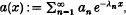where {λn} is a strictly increasing unbounded sequence of real numbers with λ1 > 0. One of the main Tauberian results proved is that if a1 ≥ 0, an > 0 for n = 2, 3, …, a(x) ≤ ∞ for all x ≥ 0, An:= a1 + a2 + … + an → ∞, an λn = o((λn+1-λn)An), an λn sn > − H(λn+1 − λn) An and 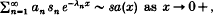then 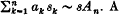A new summability method Dλ, a based on the Dirichlet series a(x) is defined and its relationship to the weighted mean method Ma investigated.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 102 , Issue 3 , November 1987 , pp. 517 - 532
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Borwein, D.. Tauberian conditions for the equivalence of weighted mean and power series methods of summability. Canad. Math. Bull. (3), 24 (1981), 309–316.CrossRefGoogle Scholar
[2]Borwein, D. and Meir, A.. A Tauberian theorem concerning weighted means and power series. Math. Proc. Cambridge Philos. Soc. 101 (1987), 283–286.CrossRefGoogle Scholar
[3]Hardy, G. H. and Littlewood, J. E.. Some theorems concerning Dirichlet's series. Messenger of Math. 43 (1914), 134–147.Google Scholar
[4]Hardy, G. H.. Orders of Infinity. Camb. Math. Tract No. 12 (Cambridge University Press, 1910).Google Scholar
[5]Hardy, G. H.. Divergent Series (Oxford University Press, 1949).Google Scholar
[6]Ishiguro, K.. A Tauberian theorem for (J, pn) summability. Proc. Japan Acad. 40 (1964), 807–812.Google Scholar
[7]Knopp, K.. Theory and Application of Infinite Series (Blackie, 1928).Google Scholar
[8]Kochanovski, A. P.. A condition for the equivalence of logarithmic methods of summability. Ukranian Math. J. 27 (1975), 229–234.Google Scholar
[9]Seneta, E.. Regularly Varying Functions. Lecture Notes in Math., Vol. 508 (Springer-Verlag, 1976).CrossRefGoogle Scholar
[10]Titchmarsh, E. C.. The Theory of Functions (Oxford University Press, second edition, 1939).Google Scholar