Research Article
Geometry of projection-generic space curves
-
- Published online by Cambridge University Press:
- 01 July 2009, pp. 115-142
-
- Article
- Export citation
Flag modules and the hit problem for the Steenrod algebra
-
- Published online by Cambridge University Press:
- 01 July 2009, pp. 143-171
-
- Article
- Export citation
Irrationality measures for some automatic real numbers
-
- Published online by Cambridge University Press:
- 10 June 2009, pp. 659-678
-
- Article
- Export citation
The abelianization of a symmetric mapping class group
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 369-388
-
- Article
- Export citation
Linking sandwich pairs
-
- Published online by Cambridge University Press:
- 15 June 2009, pp. 679-700
-
- Article
- Export citation
Harmonic morphisms from solvable Lie groups
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 389-408
-
- Article
- Export citation
On knot polynomials of annular surfaces and their boundary links
-
- Published online by Cambridge University Press:
- 01 July 2009, pp. 173-183
-
- Article
- Export citation
Isometric immersions into a homogeneous Lorentzian Heisenberg group and rigidity
-
- Published online by Cambridge University Press:
- 01 July 2009, pp. 185-204
-
- Article
- Export citation
Smooth structures and Einstein metrics on
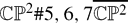
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 409-417
-
- Article
- Export citation
Finitely determined singularities of ruled surfaces in
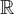 3
3
-
- Published online by Cambridge University Press:
- 22 May 2009, pp. 701-733
-
- Article
- Export citation
On the zero set of G-equivariant maps
-
- Published online by Cambridge University Press:
- 15 July 2009, pp. 735-755
-
- Article
- Export citation
The geometry of complex hyperbolic packs
-
- Published online by Cambridge University Press:
- 01 July 2009, pp. 205-234
-
- Article
- Export citation
Weak Finsler structures and the Funk weak metric
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 419-437
-
- Article
- Export citation
Proceedings of Meetings
Proceedings of the meetings held during the session 2008–2009
-
- Published online by Cambridge University Press:
- 28 September 2009, pp. 757-763
-
- Article
- Export citation
Research Article
Cobordism of Morse maps and its application to map germs
-
- Published online by Cambridge University Press:
- 01 July 2009, pp. 235-254
-
- Article
- Export citation
On characterizations of sphere-preserving maps
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 439-446
-
- Article
- Export citation
A converse to the Grace–Walsh–Szegő theorem
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 447-453
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 147 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 October 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Erratum
On the formality and strong Lefschetz property of symplectic manifolds – Erratum
-
- Published online by Cambridge University Press:
- 01 July 2009, p. 255
-
- Article
-
- You have access
- Export citation
Research Article
Graph directed Markov systems on Hilbert spaces
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 455-488
-
- Article
- Export citation



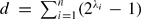 , where λ
, where λ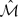

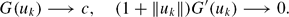
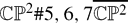
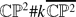 , for
, for 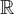
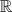
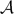
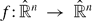 (
(