Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Odaka, Y.
2011.
The Calabi Conjecture and K-stability.
International Mathematics Research Notices,
Şuvaina, I.
2015.
The Yamabe invariant of a class of symplectic 4-manifolds.
Journal of Geometry and Physics,
Vol. 91,
Issue. ,
p.
54.


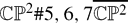
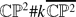 , for
, for 