Research Article
An Integral Analogue of Theta Functions and Gauss Sums in Ramanujan's Lost Notebook
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 257-265
-
- Article
- Export citation
The distribution of αp modulo one
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 267-283
-
- Article
- Export citation
Some remarks on a theorem of Parent and generalizing Ogg's conjecture
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 285-293
-
- Article
- Export citation
Motivic integration and projective bundle theorem in morphic cohomology
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 295-321
-
- Article
- Export citation
Completely positive maps into corona algebras
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 323-337
-
- Article
- Export citation
Constructive Gelfand duality for C*-algebras
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 339-344
-
- Article
- Export citation
ℝ-trees, dual laminations and compact systems of partial isometries
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 345-368
-
- Article
- Export citation
The abelianization of a symmetric mapping class group
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 369-388
-
- Article
- Export citation
Harmonic morphisms from solvable Lie groups
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 389-408
-
- Article
- Export citation
Smooth structures and Einstein metrics on
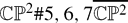
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 409-417
-
- Article
- Export citation
Weak Finsler structures and the Funk weak metric
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 419-437
-
- Article
- Export citation
On characterizations of sphere-preserving maps
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 439-446
-
- Article
- Export citation
A converse to the Grace–Walsh–Szegő theorem
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 447-453
-
- Article
- Export citation
Graph directed Markov systems on Hilbert spaces
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 455-488
-
- Article
- Export citation
Hölder-differentiability of Gibbs distribution functions
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 489-503
-
- Article
- Export citation
Homotopy type of disentanglements of multi-germs
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. 505-512
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PSP volume 147 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PSP volume 147 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 September 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation


 ⊂
⊂ 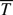
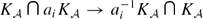 , for each
, for each 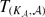 which contains an isometric copy of
which contains an isometric copy of 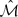
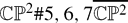
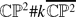 , for
, for  (
(