Research Article
Characterizing the rate of convergence in the central limit theorem. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 511-523
-
- Article
- Export citation
Orthomorphisms of archimedean vector lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-128
-
- Article
- Export citation
An intrinsic conformal Lorentz pseudodistance
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 359-371
-
- Article
- Export citation
Null hypersurfaces in Lorentzian manifolds II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 525-532
-
- Article
- Export citation
Lomonosov's hyperinvariant subspace theorem for real spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-133
-
- Article
- Export citation
Asymptotic formula for the capacitance of two oppositely charged discs
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-384
-
- Article
- Export citation
The determination of thermal stresses in dissimilar media
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 533-542
-
- Article
- Export citation
Some inequalities for martingales and applications to the study of L1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-148
-
- Article
- Export citation
Front matter
PSP volume 89 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Existence of solutions of Hammerstein equations of compact type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-158
-
- Article
- Export citation
Front matter
PSP volume 89 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 89 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Shearing transformation of a linear system at an irregular singular point
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-166
-
- Article
- Export citation
Back matter
PSP volume 89 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b6
-
- Article
-
- You have access
- Export citation
Research Article
Kneading of Lorenz type for intervals and product spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-179
-
- Article
- Export citation
On the Green's function for heterogeneous media in one-speed transport theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 181-192
-
- Article
- Export citation
Front matter
PSP volume 89 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 89 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

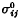 which arise when any arbitrarily shaped subregion of the upper half-space
which arise when any arbitrarily shaped subregion of the upper half-space 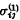 in
in 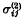 in
in 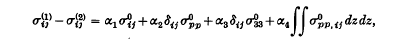
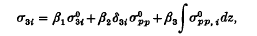
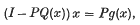

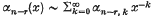 as
as 
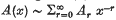 as
as 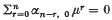 with multiplicity
with multiplicity 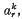 1 ≤
1 ≤